The propagation of waves in an inhomogeneous medium
































- Slides: 34

The propagation of waves in an inhomogeneous medium LL 8 sec 88

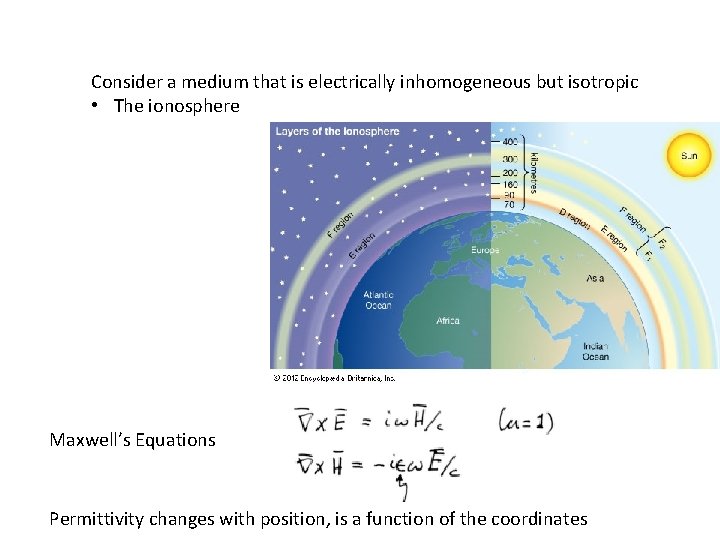
Consider a medium that is electrically inhomogeneous but isotropic • The ionosphere Maxwell’s Equations Permittivity changes with position, is a function of the coordinates

Eliminate H Diff. Eq. for E

Instead, eliminate E zero Diff. Eq. for H

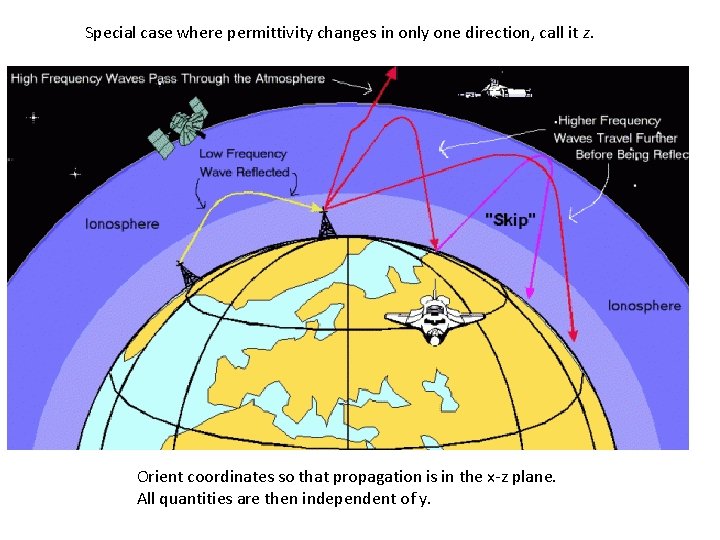
Special case where permittivity changes in only one direction, call it z. Orient coordinates so that propagation is in the x-z plane. All quantities are then independent of y.

Translational invariance in x means that the xdependence of the wave is given by exp[ikx] constant For k = 0, the field depends only on z. The wave passes normally through a layer in which e = e(z). For k non-zero, the wave passes obliquely.

First case: “E-waves” Ionosphere has equal numbers of ions and electrons

Second case: “H-waves” Equation for “H-waves”

E-wave equation

In geometrical optics, the wavelength should not change too fast along the ray of propagation This means that the wavelength hardly changes over distances of order itself. (Equality would mean that wavelength changes by its full value over distances equal to itself, Dl = l when Dz = l)

You cannot see this by simply substituting the solution into the differential equation! The proof is way more difficult! To see it, we go to quantum mechanics, where we have a similar problem!

E-waves Quantum particles 1 D permittivity variation 1 D potential These are the same equation, just with different constants. The solution of the quantum problem when the de Broglie wavelength is small compared to the characteristic distance for a change in U(z) is known: It’s the “Quasi-classical case” or “WKB approximation”.

E-waves

Solution in the quasi-classical case for quantum particles (HW)

Conditions of validity for solution Quasi-classical quantum particles Not satisfied near turning point, where E = U(z) E-waves Not satisfied at reflection point, where





A function of z. Amplitude decreases as f increases away from reflection point.














 Medium medium 35m newton
Medium medium 35m newton Cold media examples
Cold media examples Type of wave
Type of wave What waves don't require a medium
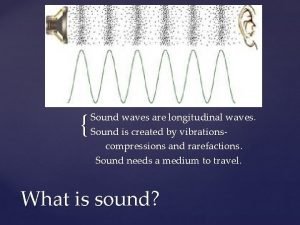
What waves don't require a medium Sound waves from a radio generally travel in which medium?
Sound waves from a radio generally travel in which medium? What waves don't require a medium
What waves don't require a medium Medium waves
Medium waves Examples of a medium in waves
Examples of a medium in waves What are waves
What are waves Lowest point of a wave
Lowest point of a wave Toh
Toh Examples of mechanical and electromagnetic waves
Examples of mechanical and electromagnetic waves Compare and contrast p waves and s waves using venn diagram
Compare and contrast p waves and s waves using venn diagram Whats a reflected sound wave
Whats a reflected sound wave An example for mechanical wave
An example for mechanical wave Similarities of mechanical and electromagnetic waves
Similarities of mechanical and electromagnetic waves Mechanical waves and electromagnetic waves venn diagram
Mechanical waves and electromagnetic waves venn diagram What is a semiconductor used for
What is a semiconductor used for Mechanical waves and electromagnetic waves
Mechanical waves and electromagnetic waves Surface waves and body waves
Surface waves and body waves Difference between constructive and destructive waves
Difference between constructive and destructive waves Difference between matter waves and electromagnetic waves
Difference between matter waves and electromagnetic waves Characteristics of a longitudinal wave
Characteristics of a longitudinal wave Seismic waves are mechanical waves
Seismic waves are mechanical waves Light waves are transverse waves true or false
Light waves are transverse waves true or false Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tính thế năng
Công thức tính thế năng Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Gấu đi như thế nào
Gấu đi như thế nào Môn thể thao bắt đầu bằng chữ đua
Môn thể thao bắt đầu bằng chữ đua