Dispersive Waves Dispersive Waves ccf Dispersive Waves C







![Apparent vs Intrinsic Dispersion interference attenuation ikxa x e ax = [Re(a)+Im(a)]x Hilbert Transform Apparent vs Intrinsic Dispersion interference attenuation ikxa x e ax = [Re(a)+Im(a)]x Hilbert Transform](https://slidetodoc.com/presentation_image/5f16ab30a183cf9edcf05206ec9a595b/image-21.jpg)

- Slides: 22

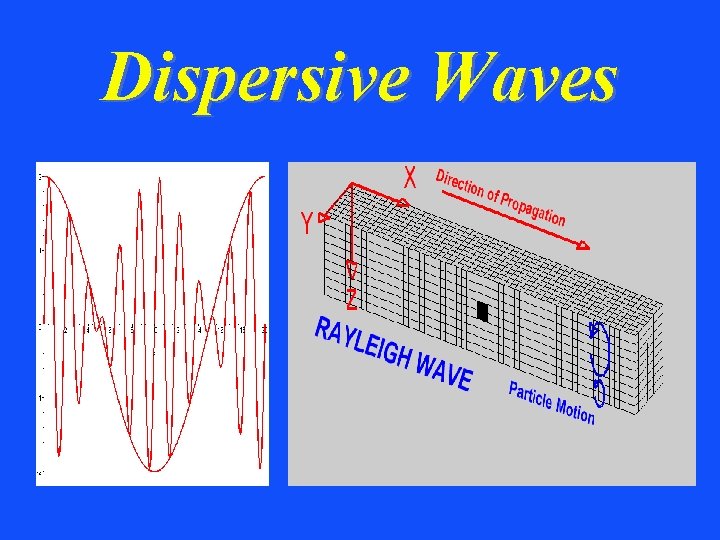
Dispersive Waves

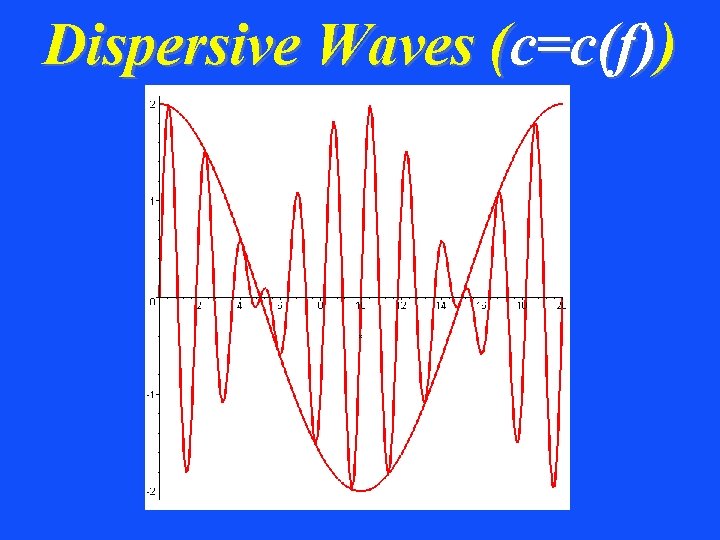
Dispersive Waves (c=c(f))

Dispersive Waves C 1= w 1/k 1 > C 2= w 2/k 2 Non-Dispersive Waves w P(x, t) = Acos(k 1 x-w 1 t) + Acos(k 2 x-w 2 t) Short l = 2 Acos( 1/2{k 1+k 2)x – ½ {w {w +w 1 )/(k 1+k 2) = Vavg 2 +w 1 k Long l )tcos( ) 1/2{k 1 -k 2)x – ½ {w 2 dw/dk~{w -w )/(k 1 -k 2) = 2 1 Vgroup Long l Short l x -w 1 )t 2

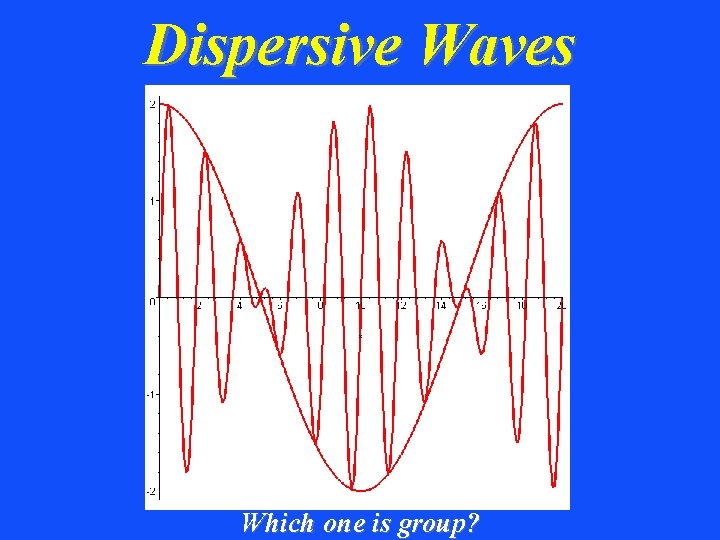
Dispersive Waves Which one is group?

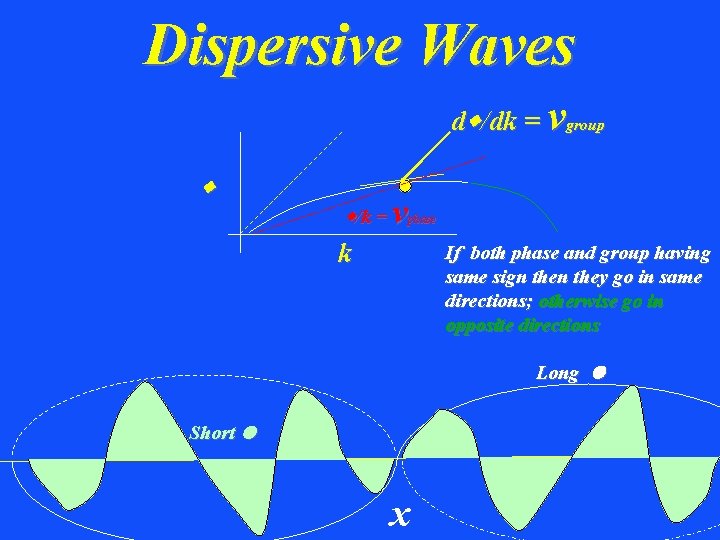
Dispersive Waves dw/dk = vgroup w w/k = v phase k If both phase and group having same sign they go in same directions; otherwise go in opposite directions Long l Short l x

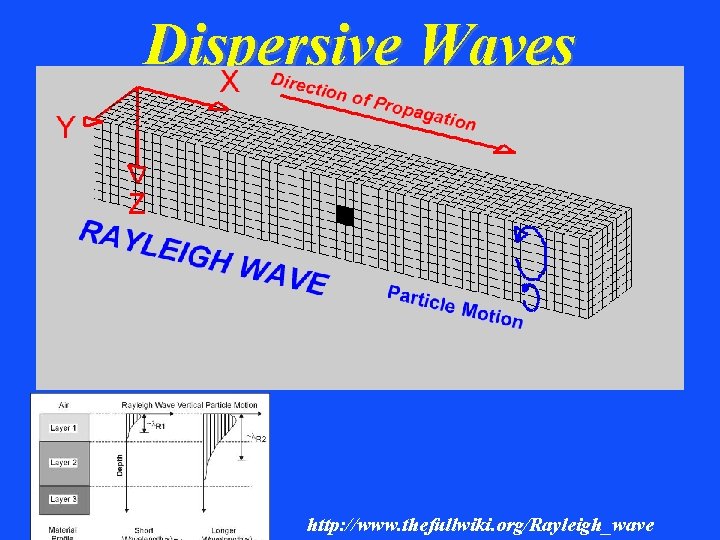
Dispersive Waves http: //www. thefullwiki. org/Rayleigh_wave

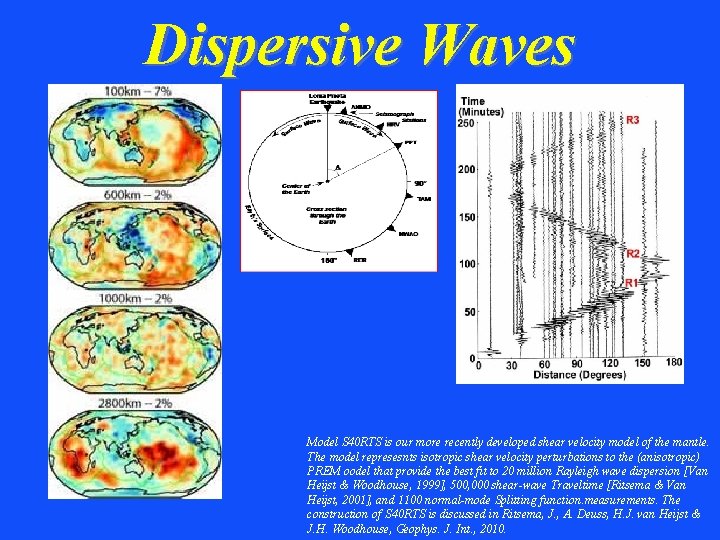
Dispersive Waves Model S 40 RTS is our more recently developed shear velocity model of the mantle. The model represesnts isotropic shear velocity perturbations to the (anisotropic) PREM oodel that provide the best fit to 20 million Rayleigh wave dispersion [Van Heijst & Woodhouse, 1999], 500, 000 shear-wave Traveltime [Ritsema & Van Heijst, 2001], and 1100 normal-mode Splitting function. measurements. The construction of S 40 RTS is discussed in Ritsema, J. , A. Deuss, H. J. van Heijst & J. H. Woodhouse, Geophys. J. Int. , 2010.

Dispersive Waves Model S 40 RTS is our more recently developed shear velocity model of the mantle. The model represesnts isotropic shear velocity perturbations to the (anisotropic) PREM oodel that provide the best fit to 20 million Rayleigh wave dispersion [Van Heijst & Woodhouse, 1999], 500, 000 shear-wave Traveltime [Ritsema & Van Heijst, 2001], and 1100 normal-mode Splitting function. measurements. The construction of S 40 RTS is discussed in Ritsema, J. , A. Deuss, H. J. van Heijst & J. H. Woodhouse, Geophys. J. Int. , 2010.

Dispersive Waves

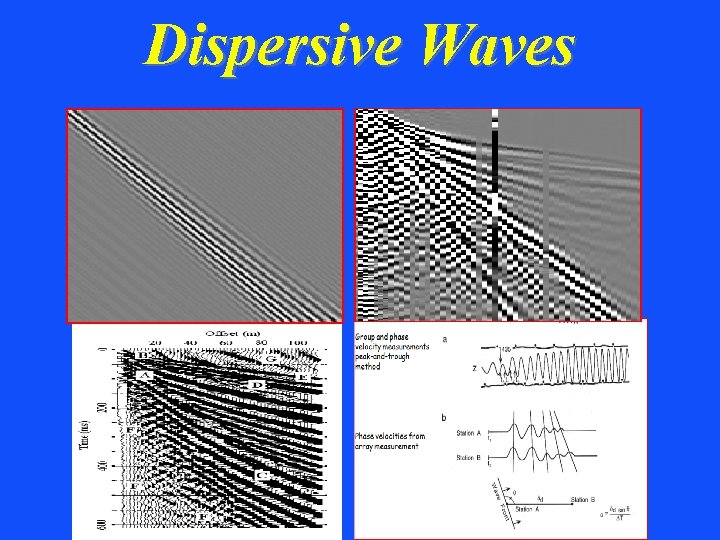
Measured Dispersion Curve K F-K transform w K K/w w Cphase = K Fund. Mode Phase velocity Fund. Mode Group velocity 1/w

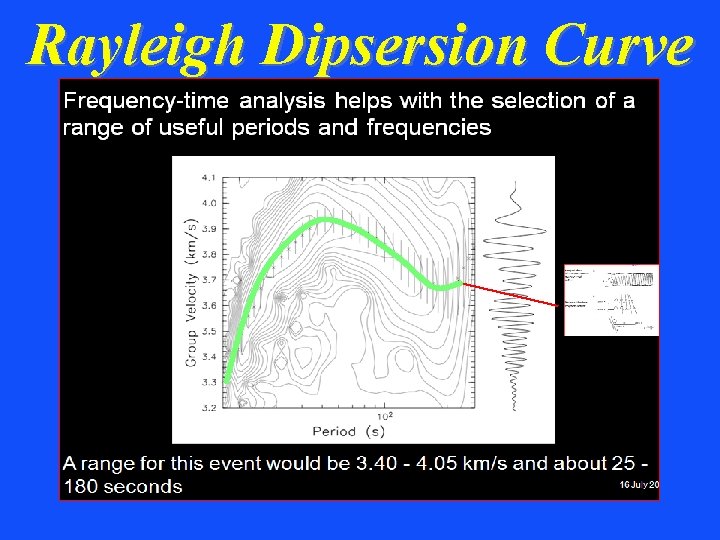
Rayleigh Dipsersion Curve

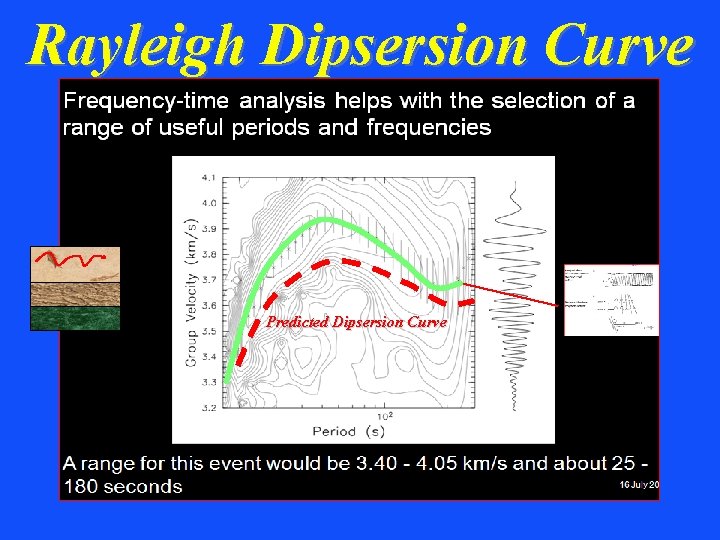
Rayleigh Dipsersion Curve Predicted Dipsersion Curve

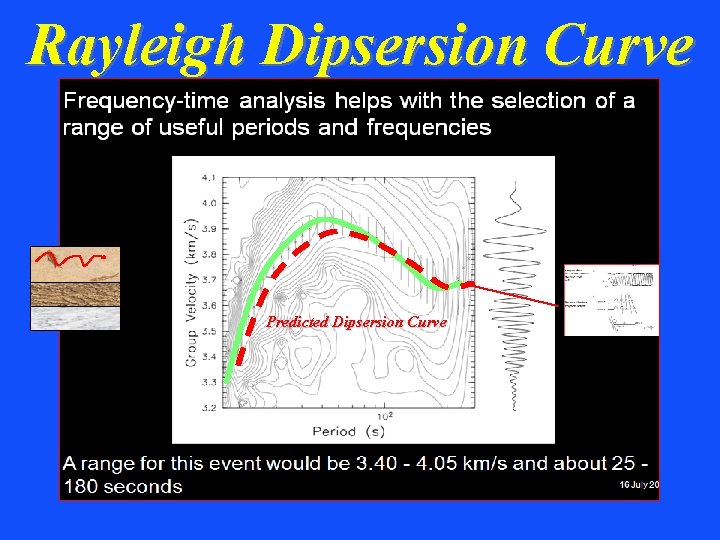
Rayleigh Dipsersion Curve Predicted Dipsersion Curve

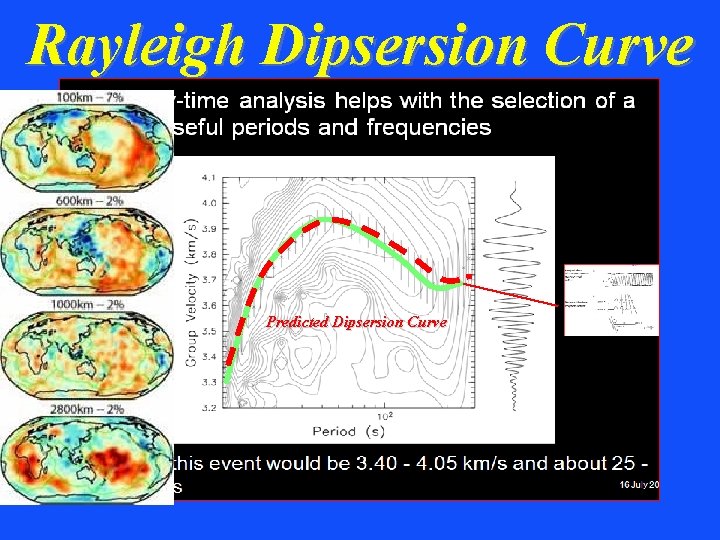
Rayleigh Dipsersion Curve Predicted Dipsersion Curve

Optical Dispersive Waves (Intrinsic Dispersion)

Water Dispersive Waves (Interference Dispersion)

NDE EM Dispersive Waves

NDE EM Dispersive Waves http: //www. ndt. net/article/wcndt 00/papers/idn 508. htm

Cloak EM Dispersive Waves By installing a transmission-line network through the structural parts of this strongly scattering object, the radiation waves, guided by the network, are made to go through the object like water finding its course (see Video 2). The transmission-line network thus makes the mesh-like object transparent ("invisible"): in other words, it does not scatter light in any direction in practice, " explains the researcher. http: //www. tkk. fi/en/current_affairs/news/view/vaitos-esineet_nakymattomiksi_siirtojohtoverkoilla/ In his dissertation, Pekka Alitalo, M. Sc. (Eng. ), developed a new method to make objects invisible. The method is based on transmission -line networks, which can transfer electromagnetic radiation through, for example, a metallic mesh-like object. There has been no previous research from this viewpoint on transparency, i. e. electromagnetic cloaking, as it is called. The idea can be applied to many different practical problems; when compared with other scientifically proved "invisibility techniques", this technique works in a comparatively wide frequency range and can be used with transmission-line structures that are easy to manufacture. Pekka Alitalo will publicly defend his doctoral thesis at Helsinki University of Technology (TKK) on 7 th August 2009.

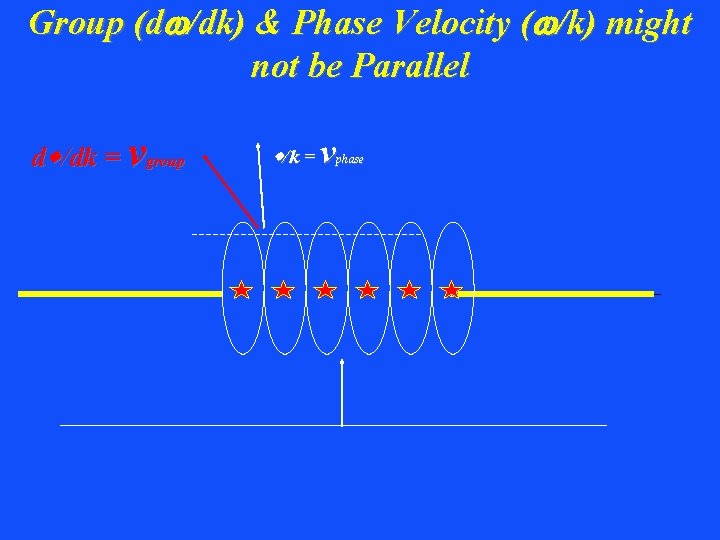
Group (dw/dk) & Phase Velocity (w/k) might not be Parallel dw/dk = vgroup w/k = v phase
![Apparent vs Intrinsic Dispersion interference attenuation ikxa x e ax ReaImax Hilbert Transform Apparent vs Intrinsic Dispersion interference attenuation ikxa x e ax = [Re(a)+Im(a)]x Hilbert Transform](https://slidetodoc.com/presentation_image/5f16ab30a183cf9edcf05206ec9a595b/image-21.jpg)
Apparent vs Intrinsic Dispersion interference attenuation ikxa x e ax = [Re(a)+Im(a)]x Hilbert Transform pair x

Summary 1. Cphase = w/k; Cgroup=dw/dk. 2. Homogeneous, non-attenuative media: Cphase = Cgroup; Group and Phase velocity vectors ||. 3. Layered Media: Guided waves, surface waves exhibit apparent dispersion (interference effects): Cphase=Cgroup cos(Cphasex-wt) cos(Cgroupx-wt) 4. Measured dispersion curves Cphase(w) VS(x, z) 5. Attenuation coefficient a complex a for satisfaction of causality. Intrinsic dispersion.
 Point ccf
Point ccf Tableau de cotation bts tourisme
Tableau de cotation bts tourisme Intranet.ccf.org
Intranet.ccf.org Icaap nedir
Icaap nedir Ccf définition
Ccf définition Common communication format (ccf)
Common communication format (ccf) Nihr central commissioning facility
Nihr central commissioning facility What is the distribution of the ccf 624
What is the distribution of the ccf 624 Short wave vs long wave radiation
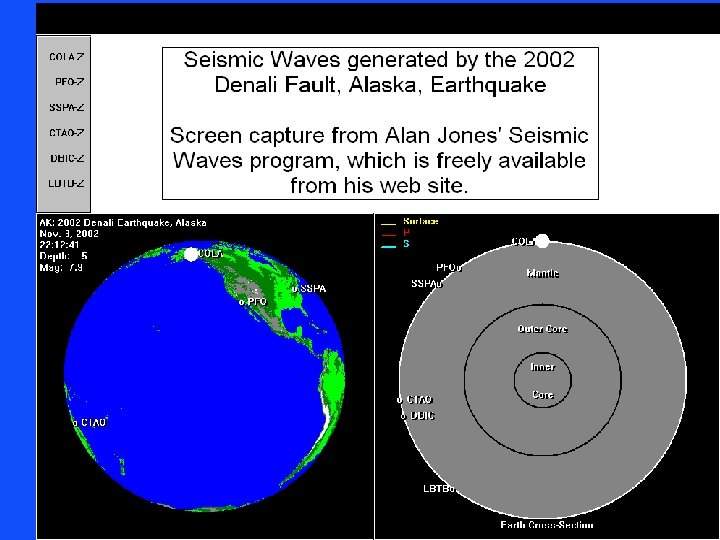
Short wave vs long wave radiation Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic Difference between mechanical and electromagnetic waves
Difference between mechanical and electromagnetic waves Examples of mechanical and electromagnetic waves
Examples of mechanical and electromagnetic waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Compare and contrast p waves and s waves using venn diagram
Compare and contrast p waves and s waves using venn diagram What type of waves are sound waves? *
What type of waves are sound waves? * Similarities of mechanical and electromagnetic waves
Similarities of mechanical and electromagnetic waves Light is electromagnetic radiation true or false
Light is electromagnetic radiation true or false Venn diagram of mechanical and electromagnetic waves
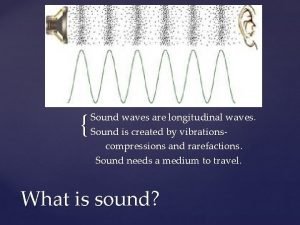
Venn diagram of mechanical and electromagnetic waves Sound waves longitudinal waves
Sound waves longitudinal waves Seismic waves
Seismic waves A matter in which waves can travel and transfer energy
A matter in which waves can travel and transfer energy Constructive waves and destructive waves difference
Constructive waves and destructive waves difference Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities