Waves Waves Electromagnetic Waves Mechanical Waves do NOT













- Slides: 28

Waves

Waves Electromagnetic Waves - Mechanical Waves - do NOT require a medium to travel though DO require a medium to travel though

Waves Electromagnetic Waves - Mechanical Waves - do NOT require a medium to travel though DO require a medium to travel though In this unit we will only be studying mechanical waves.

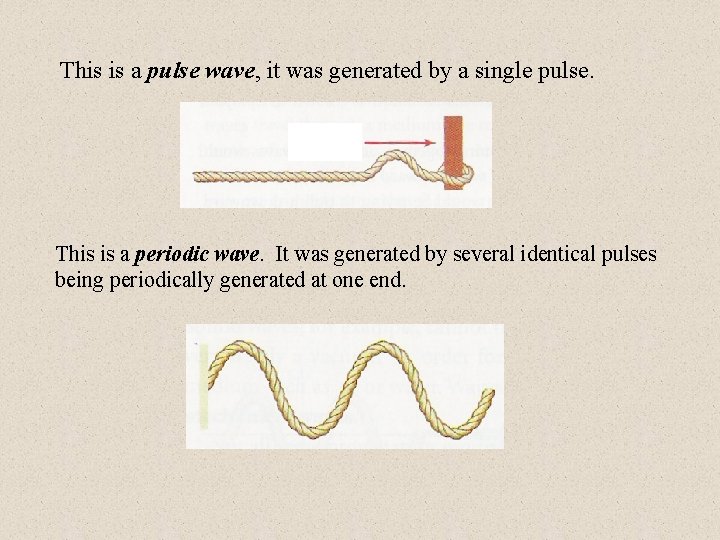
This is a pulse wave, it was generated by a single pulse. This is a periodic wave. It was generated by several identical pulses being periodically generated at one end.

Waves travel through a medium by causing the particles of that medium to “wiggle” up and down or side to side with the disturbance as it passes. The particles of the medium return to their original position after the disturbance passes and do not “move” with the wave. Mechanical waves can travel through all types of media, including gasses, liquids and solids. A wave is a means of transferring energy (but not mass) from one point to another. A mechanical wave carries a disturbance (energy) through the medium that the wave travels.

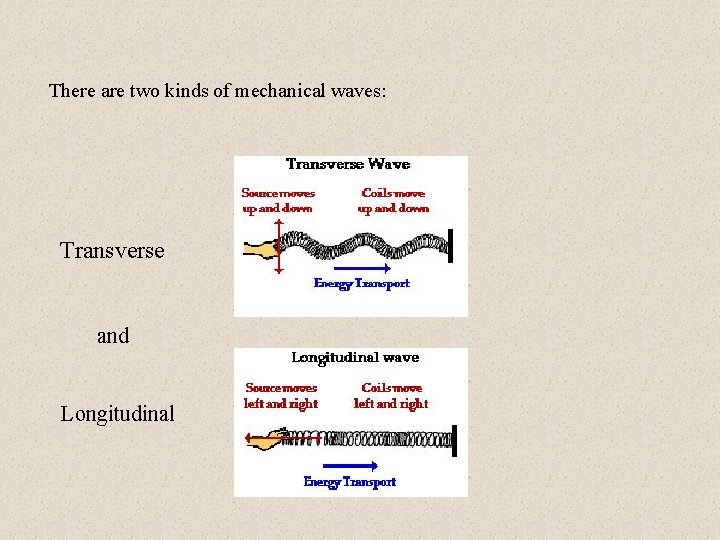
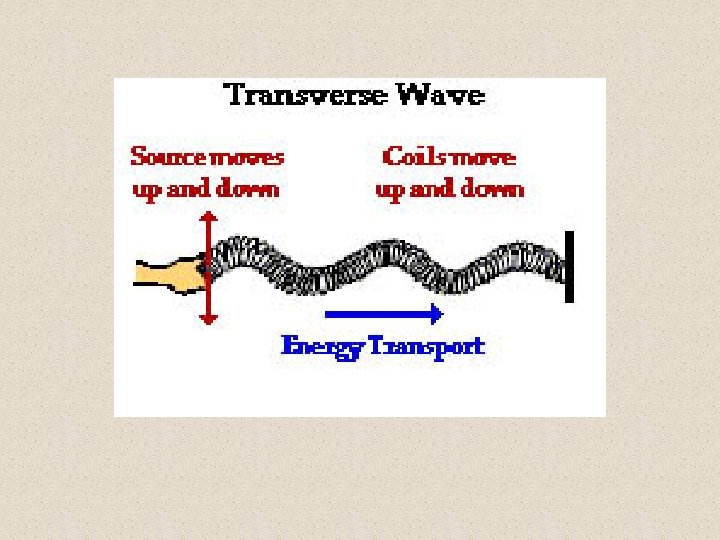
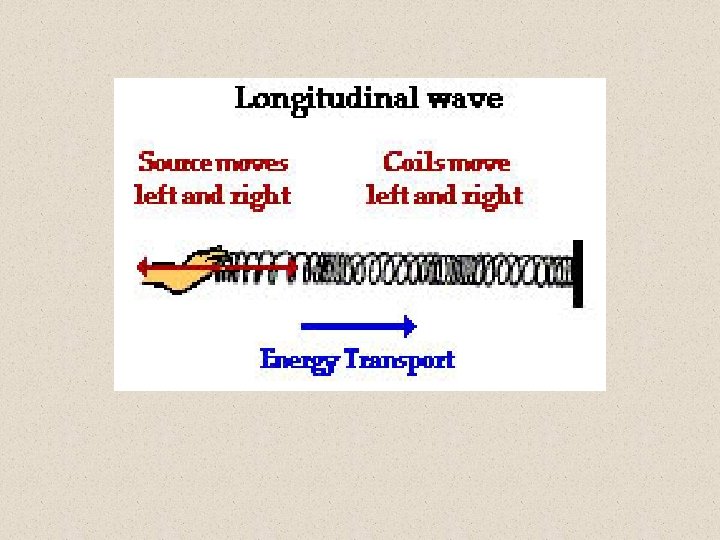
There are two kinds of mechanical waves: Transverse and Longitudinal



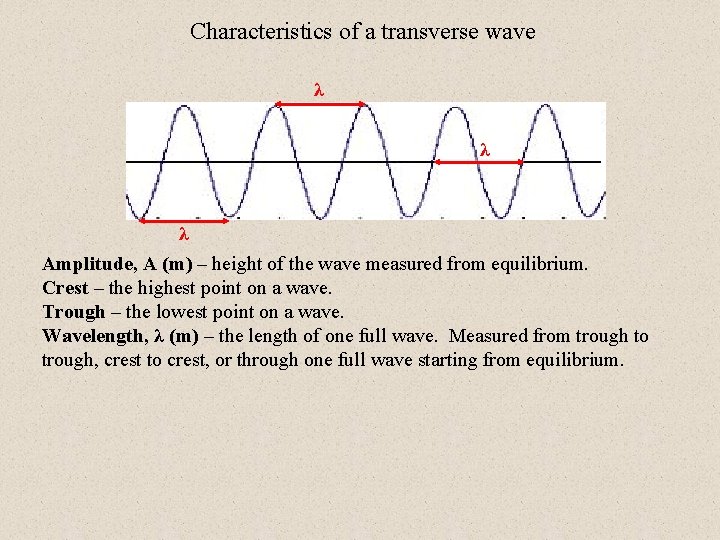
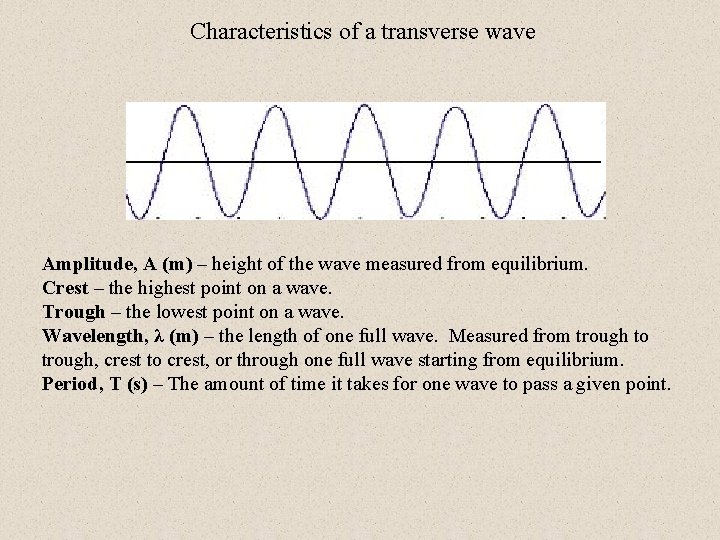
Characteristics of a transverse wave

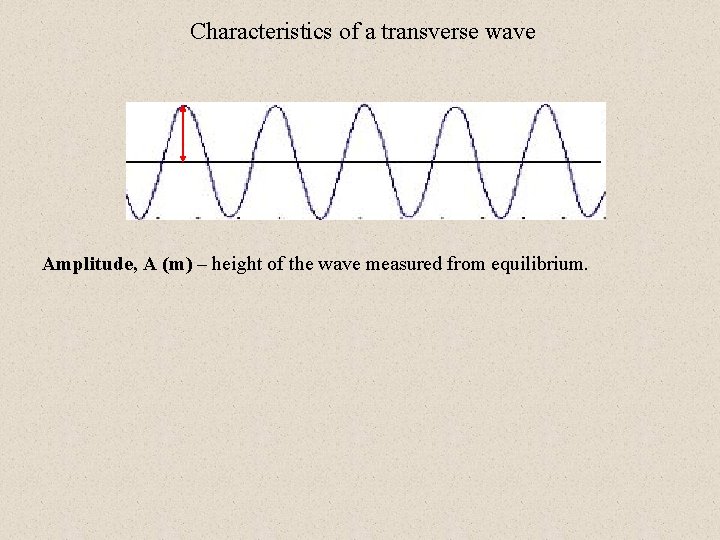
Characteristics of a transverse wave Amplitude, A (m) – height of the wave measured from equilibrium.

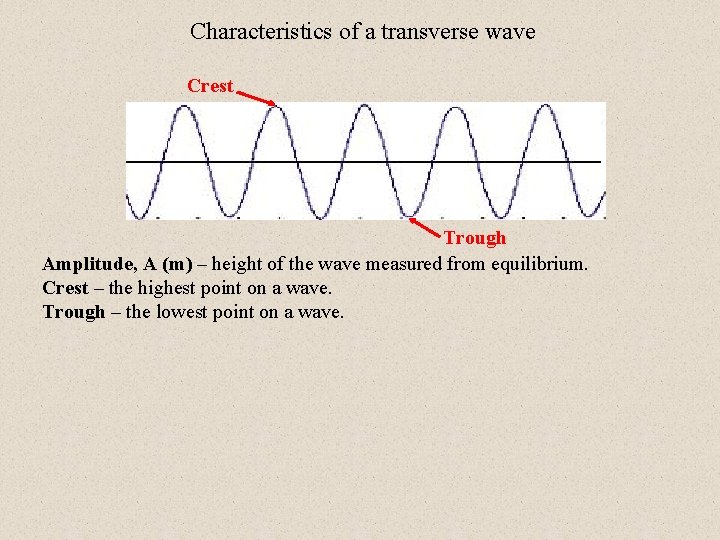
Characteristics of a transverse wave Crest Trough Amplitude, A (m) – height of the wave measured from equilibrium. Crest – the highest point on a wave. Trough – the lowest point on a wave.

Characteristics of a transverse wave λ λ λ Amplitude, A (m) – height of the wave measured from equilibrium. Crest – the highest point on a wave. Trough – the lowest point on a wave. Wavelength, λ (m) – the length of one full wave. Measured from trough to trough, crest to crest, or through one full wave starting from equilibrium.

Characteristics of a transverse wave Amplitude, A (m) – height of the wave measured from equilibrium. Crest – the highest point on a wave. Trough – the lowest point on a wave. Wavelength, λ (m) – the length of one full wave. Measured from trough to trough, crest to crest, or through one full wave starting from equilibrium. Period, T (s) – The amount of time it takes for one wave to pass a given point.

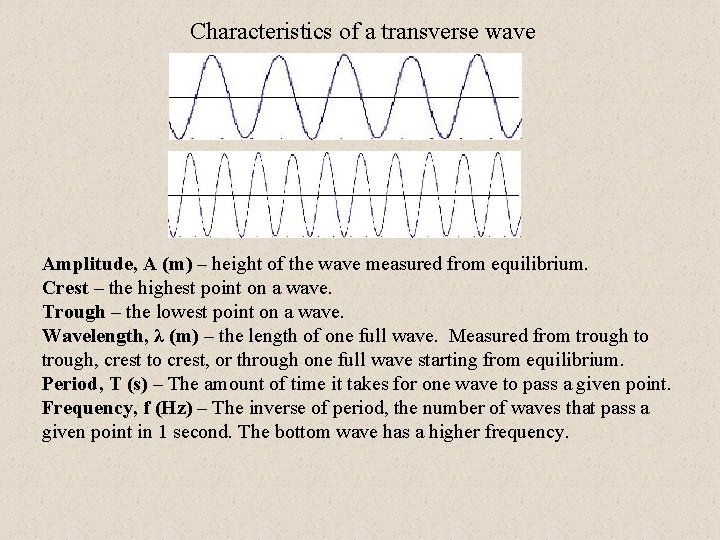
Characteristics of a transverse wave Amplitude, A (m) – height of the wave measured from equilibrium. Crest – the highest point on a wave. Trough – the lowest point on a wave. Wavelength, λ (m) – the length of one full wave. Measured from trough to trough, crest to crest, or through one full wave starting from equilibrium. Period, T (s) – The amount of time it takes for one wave to pass a given point. Frequency, f (Hz) – The inverse of period, the number of waves that pass a given point in 1 second. The bottom wave has a higher frequency.

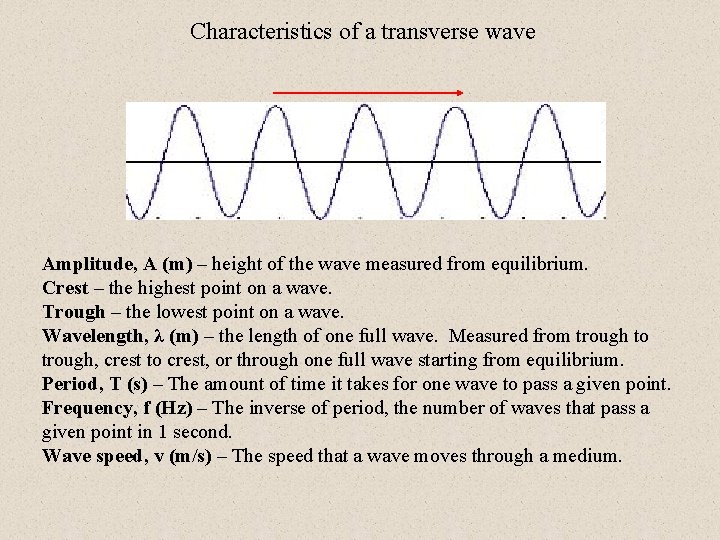
Characteristics of a transverse wave Amplitude, A (m) – height of the wave measured from equilibrium. Crest – the highest point on a wave. Trough – the lowest point on a wave. Wavelength, λ (m) – the length of one full wave. Measured from trough to trough, crest to crest, or through one full wave starting from equilibrium. Period, T (s) – The amount of time it takes for one wave to pass a given point. Frequency, f (Hz) – The inverse of period, the number of waves that pass a given point in 1 second. Wave speed, v (m/s) – The speed that a wave moves through a medium.

Equations f = 1/T Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz).

Equations f = 1/T v = d/t Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz).

Equations f = 1/T v = d/t v = d (1/t) Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz).

Equations f = 1/T v = d/t v = d (1/t) Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz). If the distance the wave travels is 1 wavelength, then the time it takes to travel that distance is 1 period (by definition). So we could also write the equation

Equations f = 1/T v = d/t v = d (1/t) v = λ(1/T) Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz). If the distance the wave travels is 1 wavelength, then the time it takes to travel that distance is 1 period (by definition). So we could also write the equation

Equations f = 1/T v = d/t v = d (1/t) v = λ(1/T) v = λf Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz). If the distance the wave travels is 1 wavelength, then the time it takes to travel that distance is 1 period (by definition). So we could also write the equation

Equations f = 1/T v = d/t v = d (1/t) v = λ(1/T) v = λf Because frequency and period are the inverse of each other. Frequency is measured in the unit 1/s, also known as the Hertz (Hz). If the distance the wave travels is 1 wavelength, then the time it takes to travel that distance is 1 period (by definition). So we could also write the equation

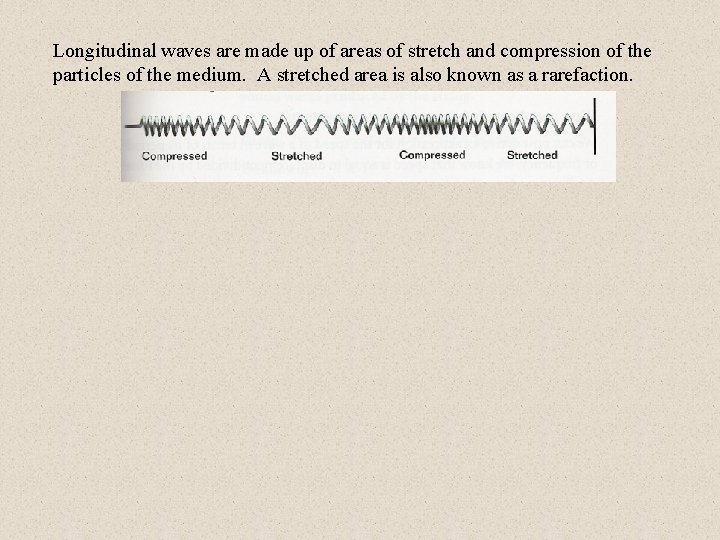
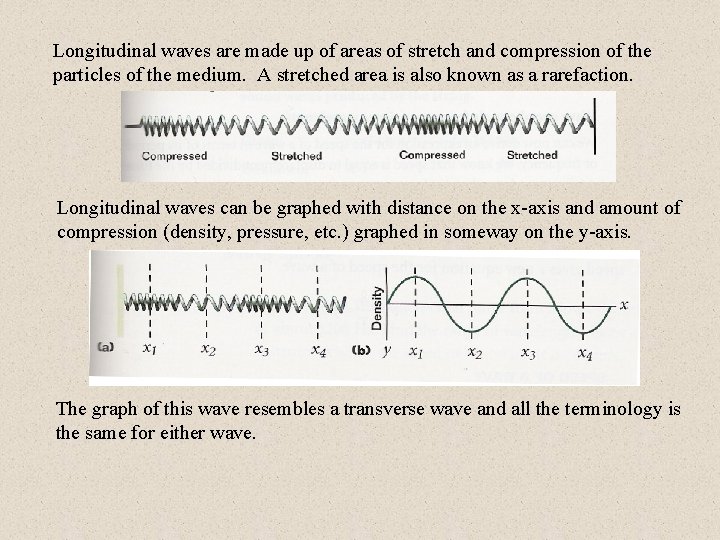
Longitudinal waves are made up of areas of stretch and compression of the particles of the medium. A stretched area is also known as a rarefaction.

Longitudinal waves are made up of areas of stretch and compression of the particles of the medium. A stretched area is also known as a rarefaction. Longitudinal waves can be graphed with distance on the x-axis and amount of compression (density, pressure, etc. ) graphed in someway on the y-axis. The graph of this wave resembles a transverse wave and all the terminology is the same for either wave.

Interference and superposition When two waves pass through the same space, the waves do not interact. Instead, each one acts on the particles in that space independently and then the waves move through each other without affecting the other. So if a wave tending to move a particle 1 unit upward passes at the same moment another wave tending to move the same particle 1 unit upward passes, the particle will move 2 units upward, this is known as superposition, the waves simply add (or subtract) their effect on the medium as they cross.

For example: y 2 is moving rigth, y 1 is moving left just about to meet when they meet, max displacement = y 1 + y 2, waves are adding waves pass through, y 1 is still moving left and y 2 right

Standing waves When a wave is produced on a string or slinky it will travel down to one end and then reflect back. If the wave is of the right frequency, the reflected waves will constructively and destructively interfere in such a way to make a standing wave. Different frequencies will produce a different number of standing waves.

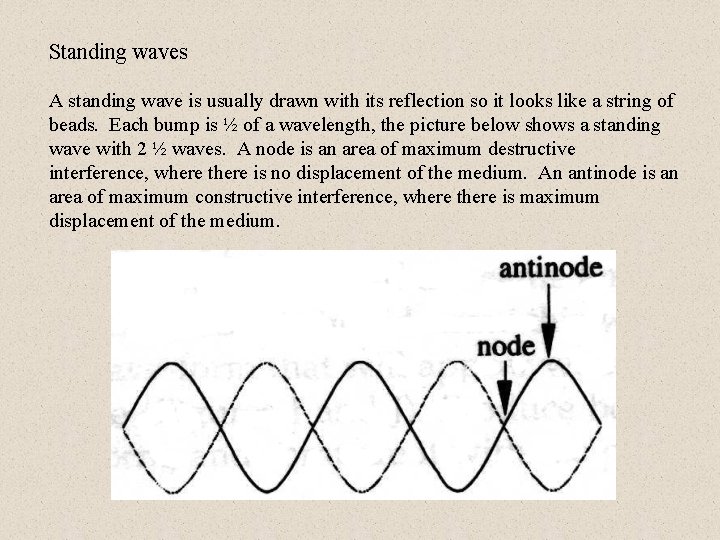
Standing waves A standing wave is usually drawn with its reflection so it looks like a string of beads. Each bump is ½ of a wavelength, the picture below shows a standing wave with 2 ½ waves. A node is an area of maximum destructive interference, where there is no displacement of the medium. An antinode is an area of maximum constructive interference, where there is maximum displacement of the medium.