Sts Cyril and Methodius University Skopje FACULTY OF

Sts. Cyril and Methodius University - Skopje FACULTY OF ELECTRICAL ENGINEERING AND INFORMATION TECHNOLOGIIES Semiconductor Device Modeling Lecture 7. Particle-Based Device Simulation Methods 1. Free-flight Generation 2. Final State After Scattering 3. Ensemble Monte-Carlo Simulation 4. Device Simulation Using Particles – Monte Carlo Device Simulation Knowledge Alliance 562206 -EPP-1 -2015 -1 -BG-EPPKA 2 -KA Micro-Electronics Cloud Alliance (MECA)

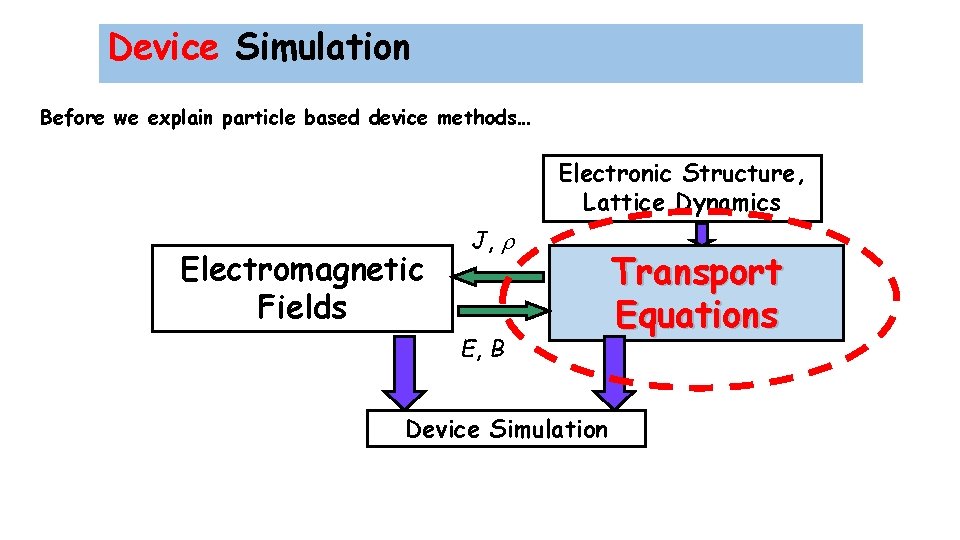
Device Simulation Before we explain particle based device methods… Electronic Structure, Lattice Dynamics Electromagnetic Fields J, r E, B Device Simulation Transport Equations

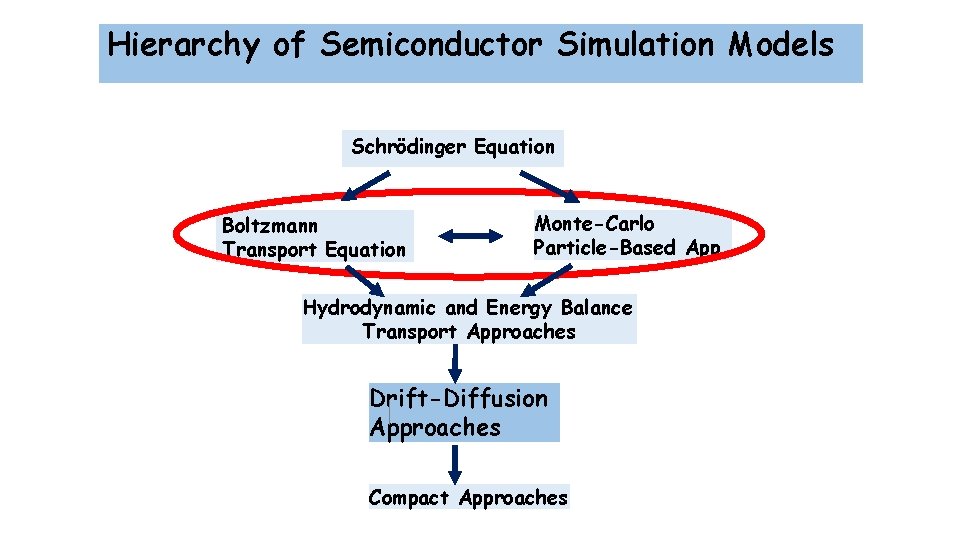
Hierarchy of Semiconductor Simulation Models Schrödinger Equation Boltzmann Transport Equation Monte-Carlo Particle-Based App. Hydrodynamic and Energy Balance Transport Approaches Drift-Diffusion Approaches Compact Approaches

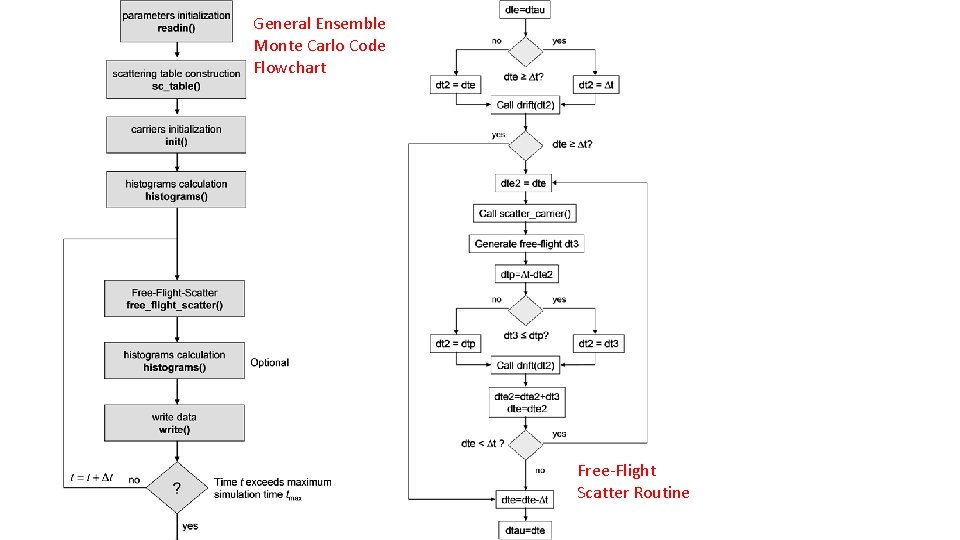
Monte Carlo Method for the Solution of the Boltzmann Transport Equation Outline Path Integral Solution of the Boltzmann Transport Equation (BTE) Ways of Solving BTE The Monte Carlo Method Described Scattering Tables Construction Carrier Initialization in Momentum Space Free-flight Sequence Choice of Scattering Events Choice of Final State After Scattering Free-flight-scatter Flow-Chart Ensemble Monte Carlo Ensemble Averages Representative Simulation Results Inclusion of the Pauli Exclusion Principle

Path Integral Solution of the BTE �The path integral solution of the Boltzmann Transport Equation (BTE), where L=N t and tn=n t, is of the form: K. K. Thornber and Richard P. Feynman, Phys. Rev. B 1, 4099 (1970).

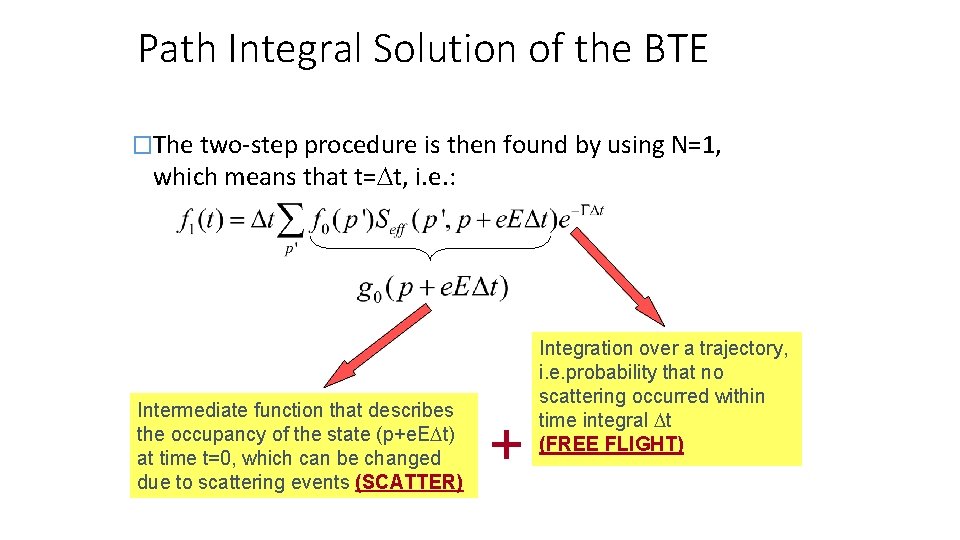
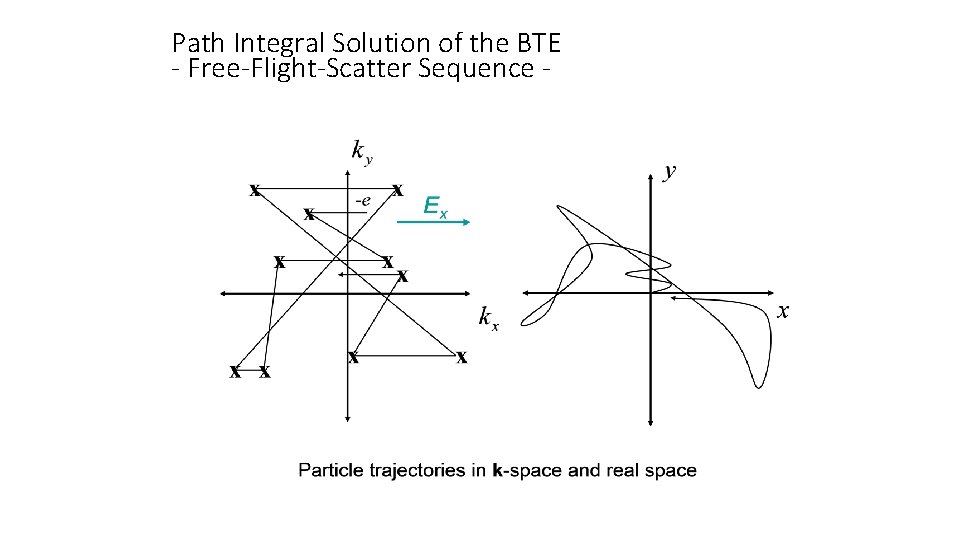
Path Integral Solution of the BTE �The two-step procedure is then found by using N=1, which means that t= t, i. e. : Intermediate function that describes the occupancy of the state (p+e. E t) at time t=0, which can be changed due to scattering events (SCATTER) + Integration over a trajectory, i. e. probability that no scattering occurred within time integral t (FREE FLIGHT)

Path Integral Solution of the BTE Using path integral formulation to the BTE one can show that one can decompose the solution procedure into two components: • • Carrier free-flights that are interrupted by scattering events • Memory-less scattering events that change the momentum and the energy of the particle instantaneously

Path Integral Solution of the BTE - Free-Flight-Scatter Sequence -

Ways of solving the BTE �Single particle Monte Carlo Technique Follow single particle for long enough time to collect sufficient statistics Practical for characterization of bulk materials or inversion layers �Ensemble Monte Carlo Technique MUST BE USED when modeling SEMICONDUCTOR DEVICES to have the complete self-consistency built in Carlo Jacoboni and Lino Reggiani, The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials, Rev. Mod. Phys. 55, 645 - 705 (1983).

The Monte Carlo Method - Scattering Tables Construction • First, bandstructure of the material is chosen • For consideration of electron transport in silicon material system, 6 equivalent conduction band valleys are considered • For the case of Ga. As material, for example, 3 non-equivalent valleys must be accounted for proper treatment of high field transport in this material system. Namely, the gamma, X and L valleys must be taken into consideration if high field transport has to be accounted for properly. • Next, relevant scattering mechanisms are identified • For silicon material system relevant scattering mechanisms are acoustic phonon scattering, Coulomb scattering and intervalley gand f-type of phonon scattering • For the case of Ga. As, relevant scattering mechanisms are acoustic phonon scattering, polar optical phonon scattering, Coulomb scattering and non-equivalent intervalley phonon scattering

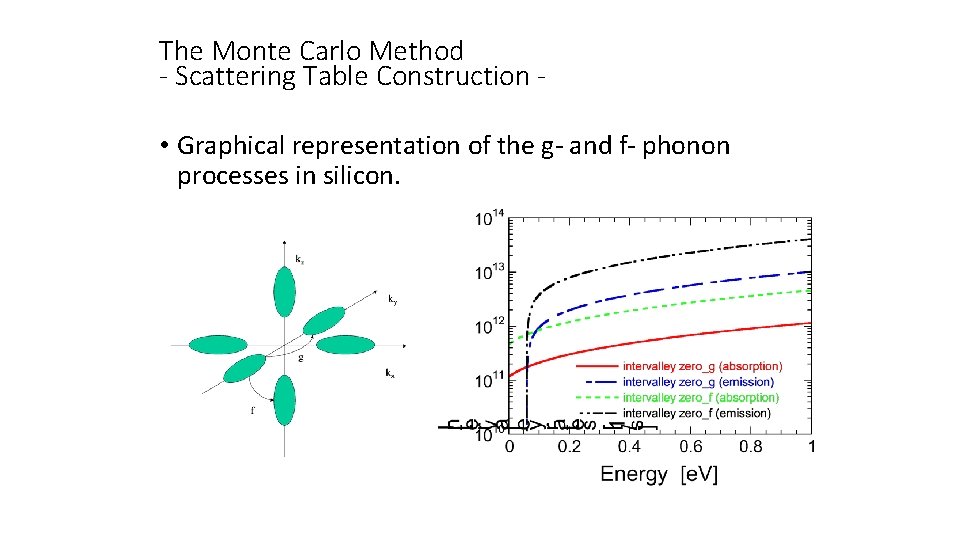
The Monte Carlo Method - Scattering Table Construction • Continuing on the intervalley scattering in silicon, it can be due to g- and f-phonons. • G-phonons move the carriers on the opposite end of the same axis. There is only one final valley into which the phonons can scatter due to g-phonons and the valley degeneracy of this scattering mechanism is therefore 1. • F-phonons move the electrons from the, for example, (100) valley into a (010) valley, or (001) valley, just to name a few. Indeed there are 4 final valleys into which the electrons can scatter into and the valley degeneracy factor f-phonons is 4. • A graphical illustration of the g- and the f-phonon processes in silicon is shown in the following slide,

The Monte Carlo Method - Scattering Table Construction • Graphical representation of the g- and f- phonon processes in silicon.

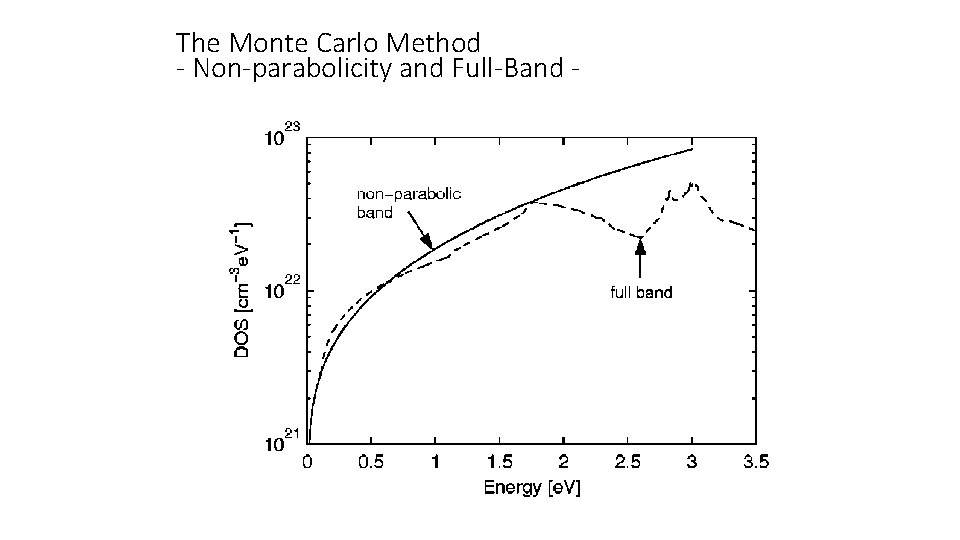
The Monte Carlo Method - Non-parabolicity and Full-Band -

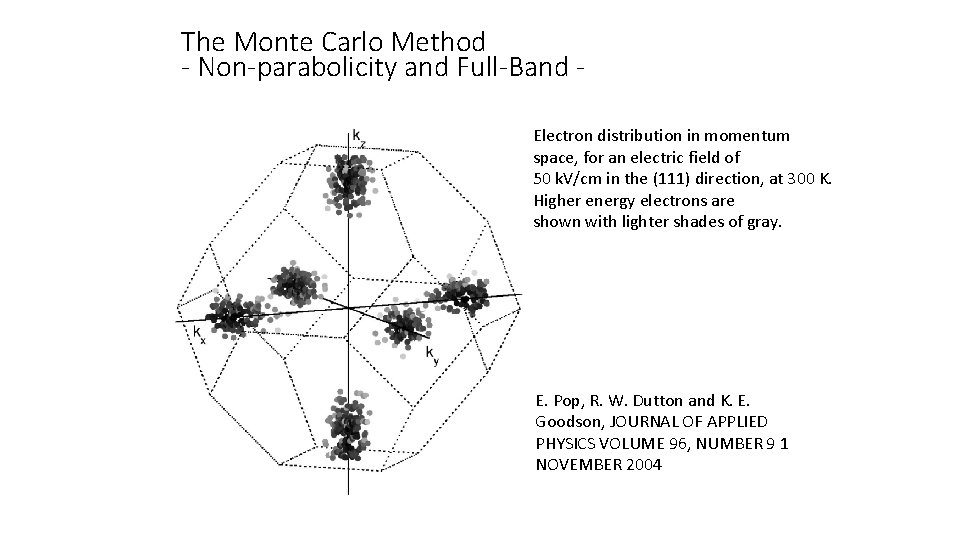
The Monte Carlo Method - Non-parabolicity and Full-Band Electron distribution in momentum space, for an electric field of 50 k. V/cm in the (111) direction, at 300 K. Higher energy electrons are shown with lighter shades of gray. E. Pop, R. W. Dutton and K. E. Goodson, JOURNAL OF APPLIED PHYSICS VOLUME 96, NUMBER 9 1 NOVEMBER 2004

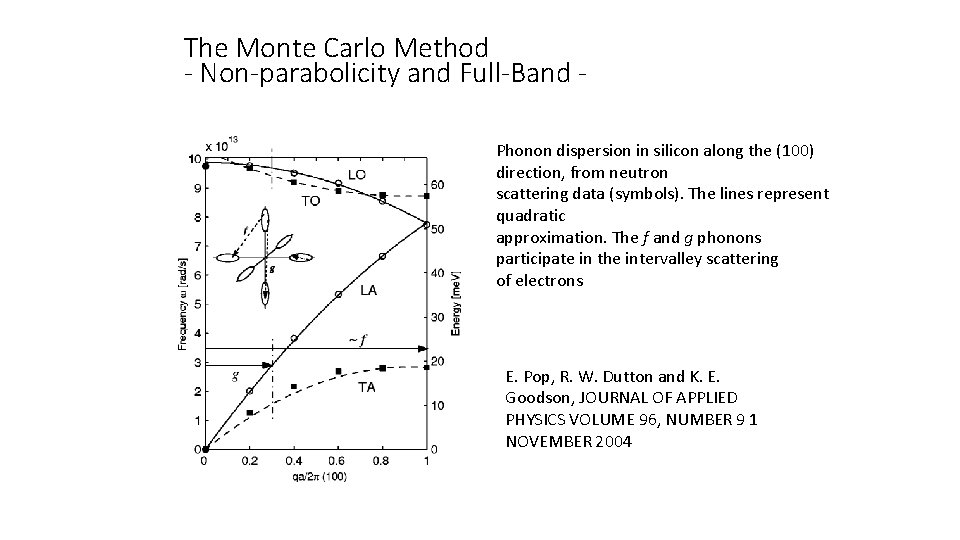
The Monte Carlo Method - Non-parabolicity and Full-Band Phonon dispersion in silicon along the (100) direction, from neutron scattering data (symbols). The lines represent quadratic approximation. The f and g phonons participate in the intervalley scattering of electrons E. Pop, R. W. Dutton and K. E. Goodson, JOURNAL OF APPLIED PHYSICS VOLUME 96, NUMBER 9 1 NOVEMBER 2004

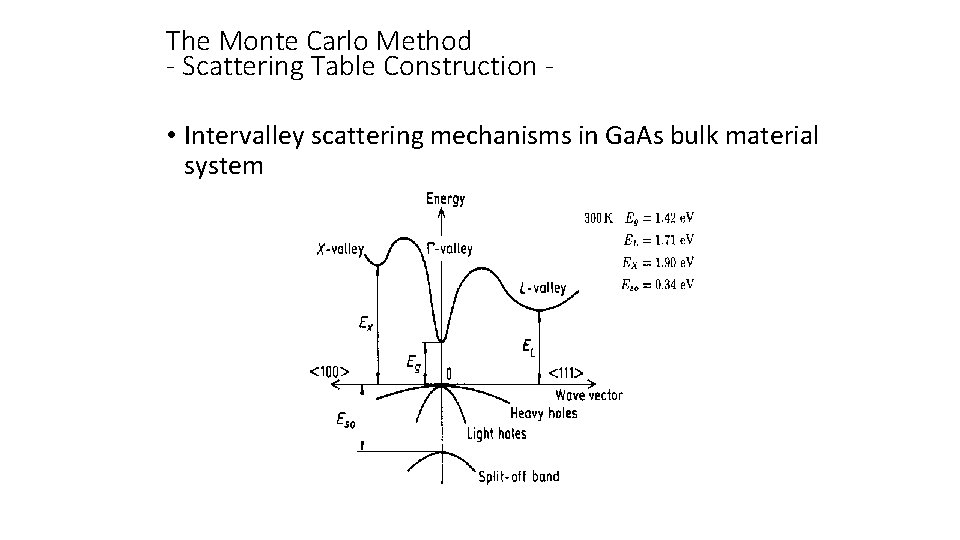
The Monte Carlo Method - Scattering Table Construction • For the case of Ga. As we have three non-equivalent valleys. Namely, we gave the gamma valley (single), the three X valleys and the four L valleys. Then, a scattering table is needed for each of these three nonequivalent valleys. The possible intervalley transittions are: • For gamma valley: gamma X (3) , gamma L(4) • For X valley: X gamma (1), X X(2), X L(4) • For the L-valley, we have: L gamma(1), L X(3), L L(3) • The graphical representation of these possible transitions is shown in the next slide.

The Monte Carlo Method - Scattering Table Construction • Intervalley scattering mechanisms in Ga. As bulk material system

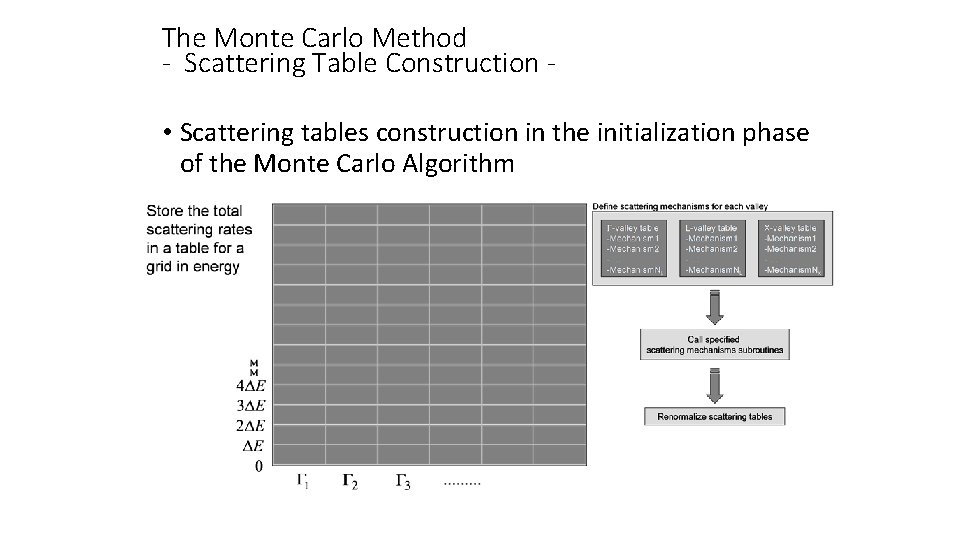
The Monte Carlo Method - Scattering Table Construction • Scattering tables construction in the initialization phase of the Monte Carlo Algorithm

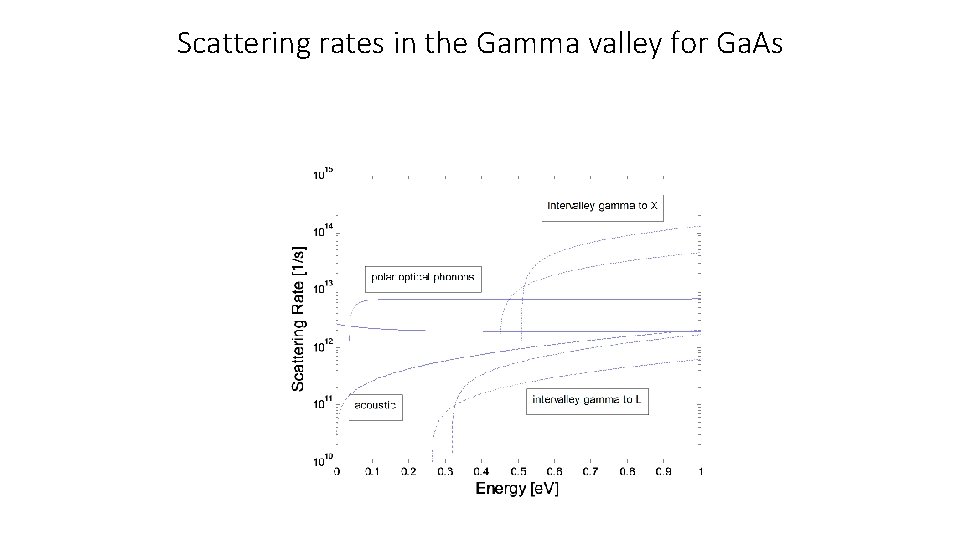
Scattering rates in the Gamma valley for Ga. As

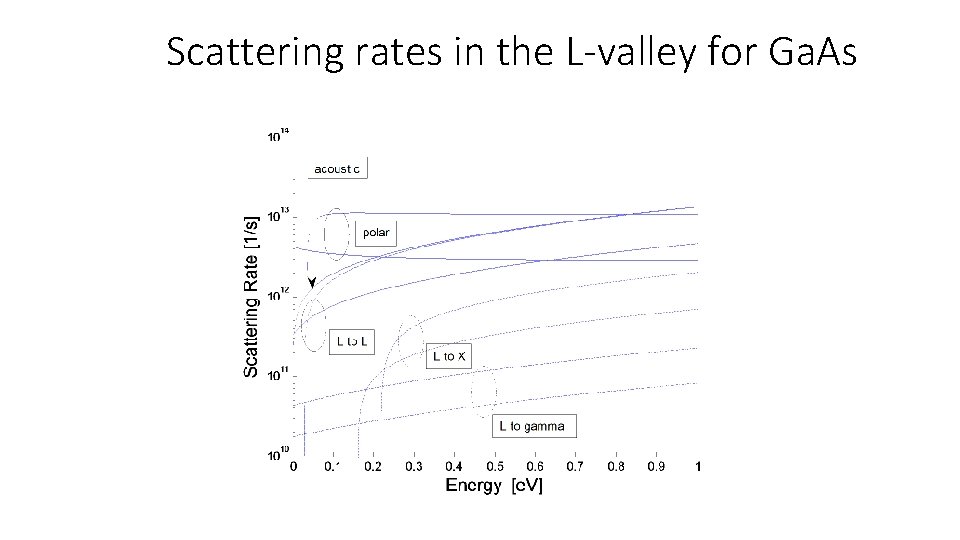
Scattering rates in the L-valley for Ga. As

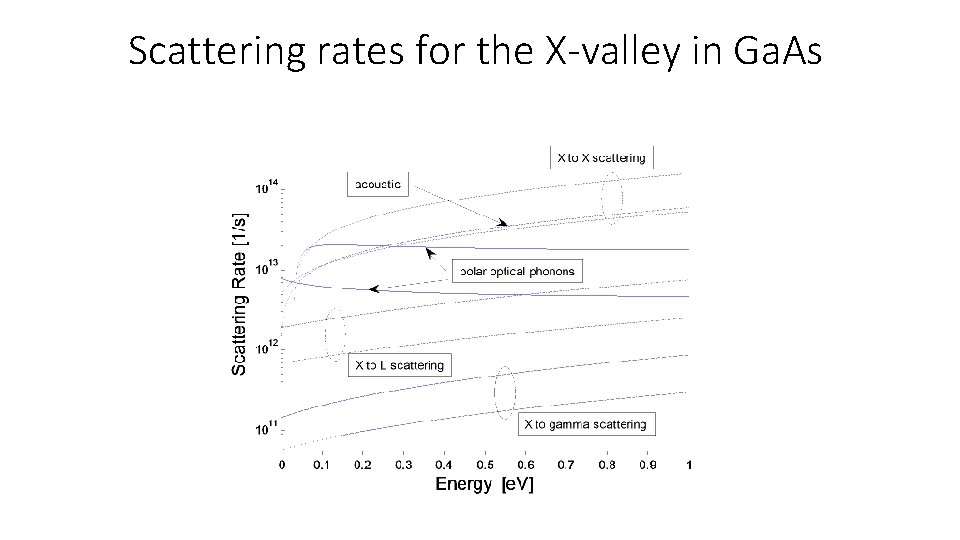
Scattering rates for the X-valley in Ga. As

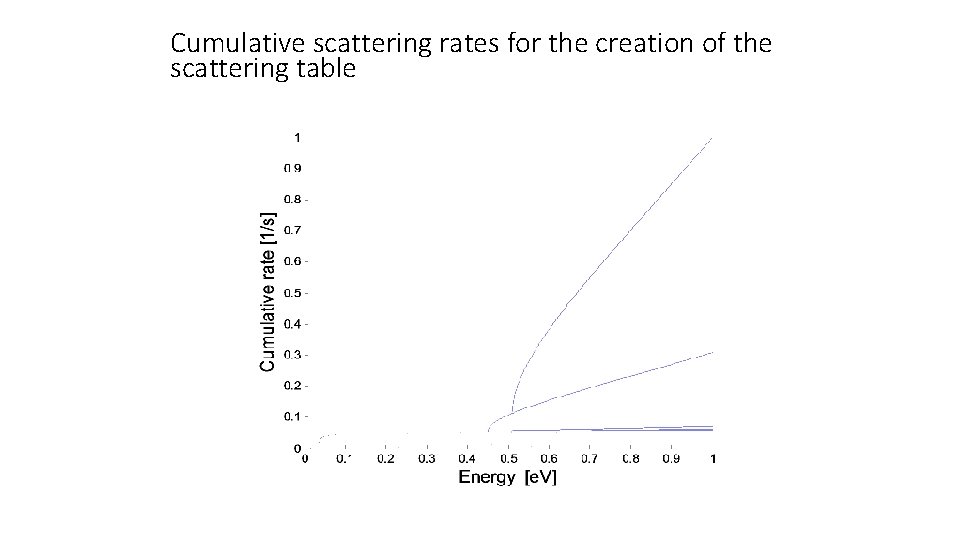
Cumulative scattering rates for the creation of the scattering table

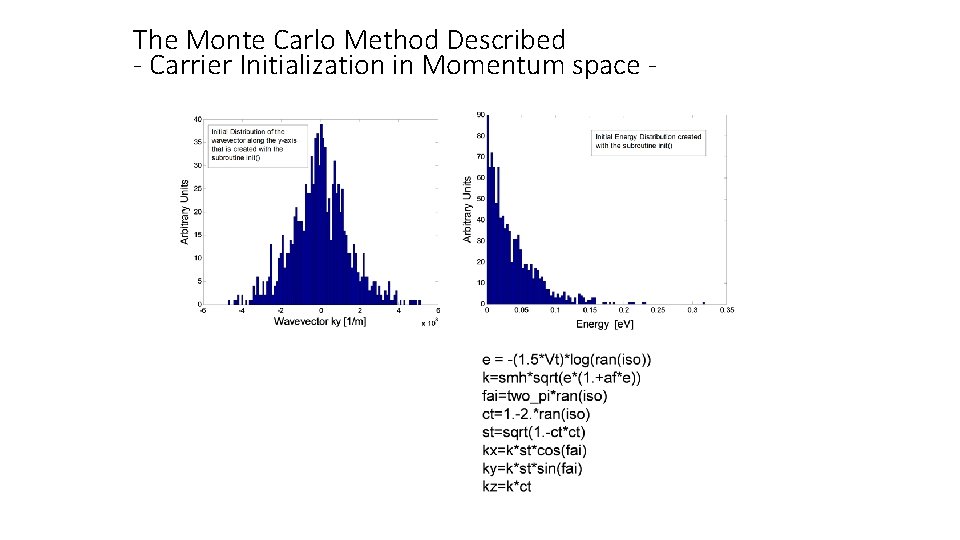
The Monte Carlo Method Described - Carrier Initialization in Momentum space -

The Monte Carlo Method Described - Carrier Free-Flights • In general the carrier free-flights are obtained by inverting the following equation • Rees introduced the concept of self-energy which allows for the analytical solution of the integral:

The Monte Carlo Method Described - Carrier Free-Flights -

The Monte Carlo Method Described - Carrier Free-Flights -

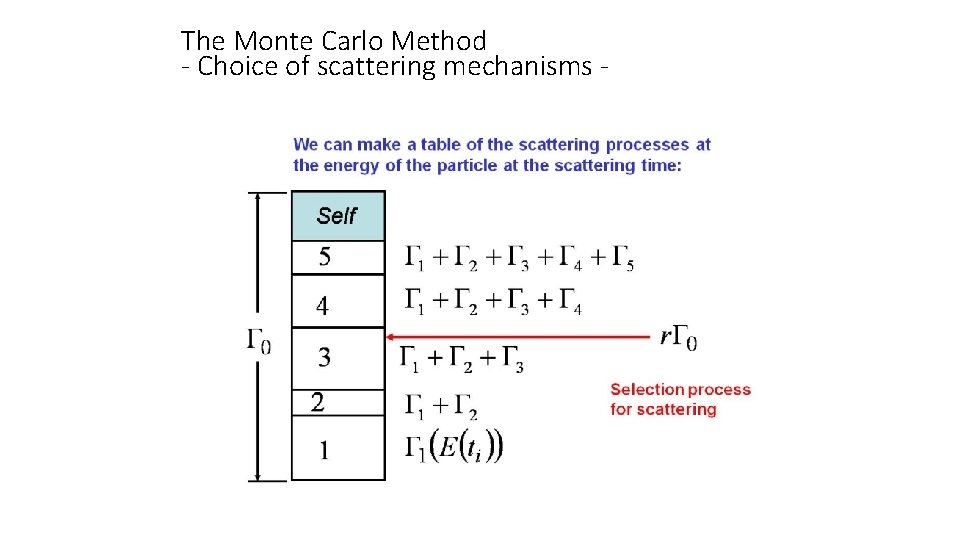
The Monte Carlo Method - Choice of scattering mechanisms • After a free-flight is completed one has to choose what type of scattering mechanism will take place. • This is accomplished with a selection of a random number uniformly distributed between 0 and 1. • It is assumed in this process that the cumulative scattering tables are normalized to unity. • A bin in the scattering table is then selected that corresponds to the particle energy. • The random number is compared against the values of various cells that denote the probability of a given scattering event to occur at the carrier energy.

The Monte Carlo Method - Choice of scattering mechanisms -

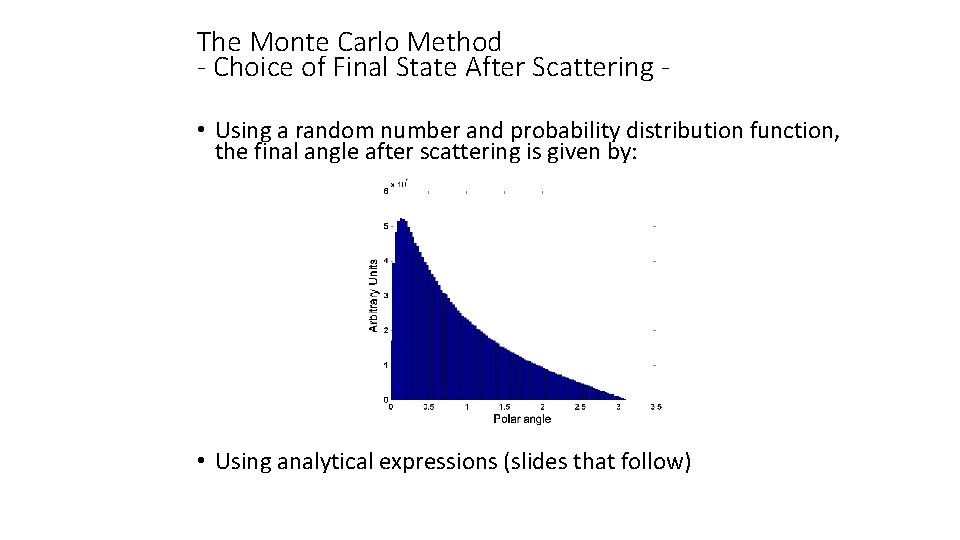
The Monte Carlo Method - Choice of Final State After Scattering • Using a random number and probability distribution function, the final angle after scattering is given by: • Using analytical expressions (slides that follow)

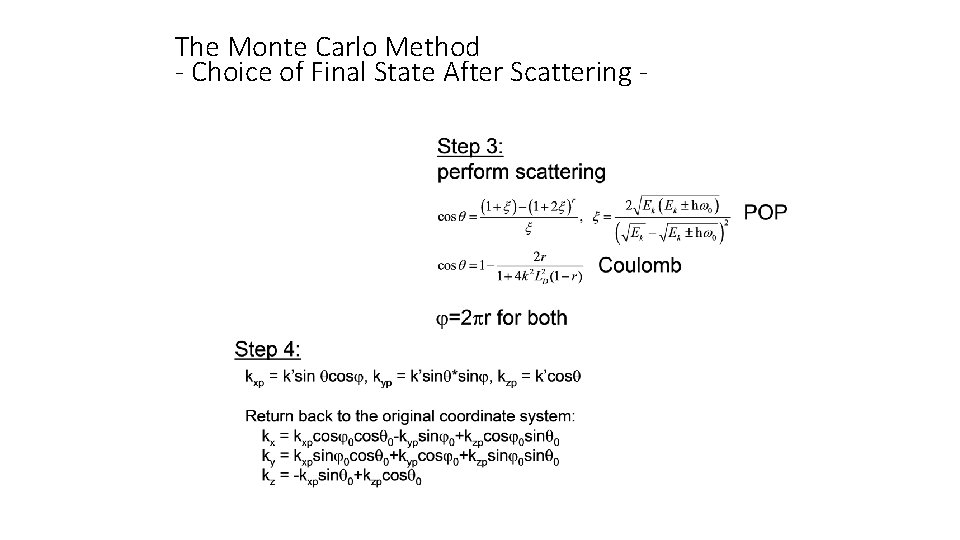
The Monte Carlo Method - Choice of Final State After Scattering • The analytical model is based on the following expressions for the calculation of the final angle after scattering:

The Monte Carlo Method - Choice of Final State After Scattering -

The Monte Carlo Method - Choice of Final State After Scattering -

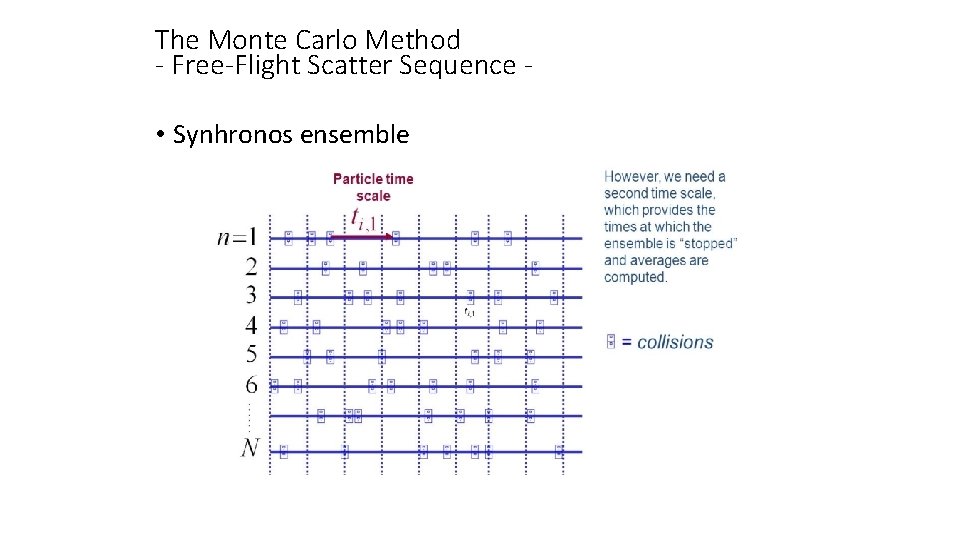
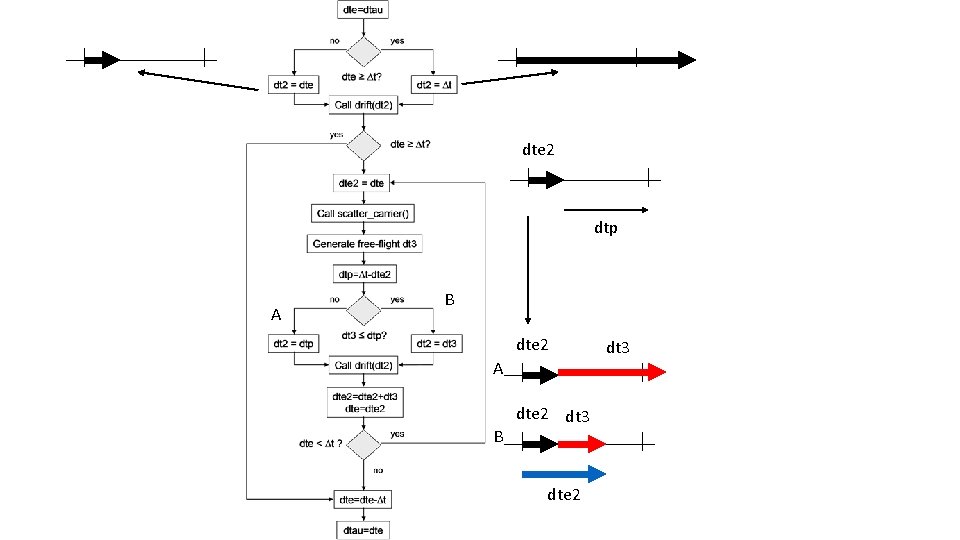
The Monte Carlo Method - Free-Flight Scatter Sequence • Synhronos ensemble

dte 2 dtp A B dte 2 dt 3

General Ensemble Monte Carlo Code Flowchart Free-Flight Scatter Routine

The Monte Carlo Method - Ensemble Averages -

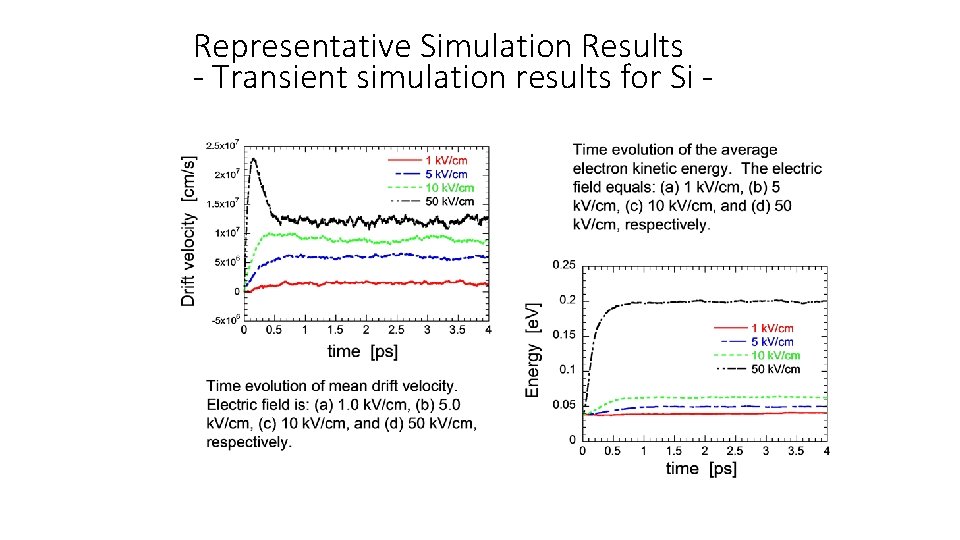
Representative Simulation Results - Transient simulation results for Si -

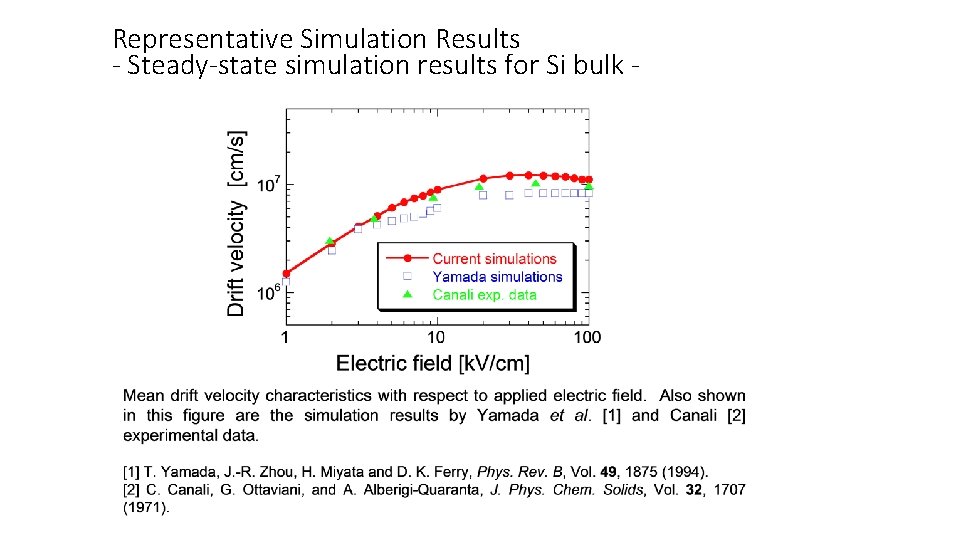
Representative Simulation Results - Steady-state simulation results for Si bulk -

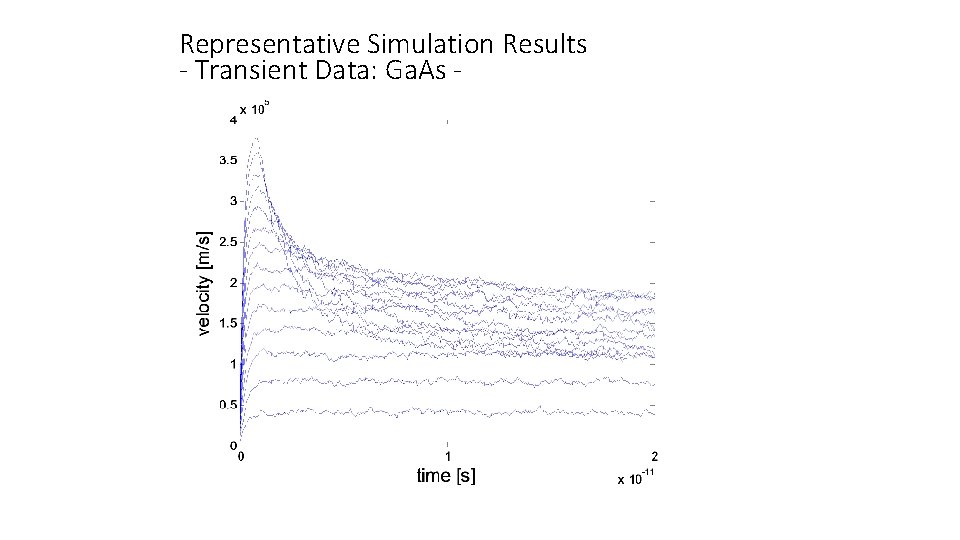
Representative Simulation Results - Transient Data: Ga. As -

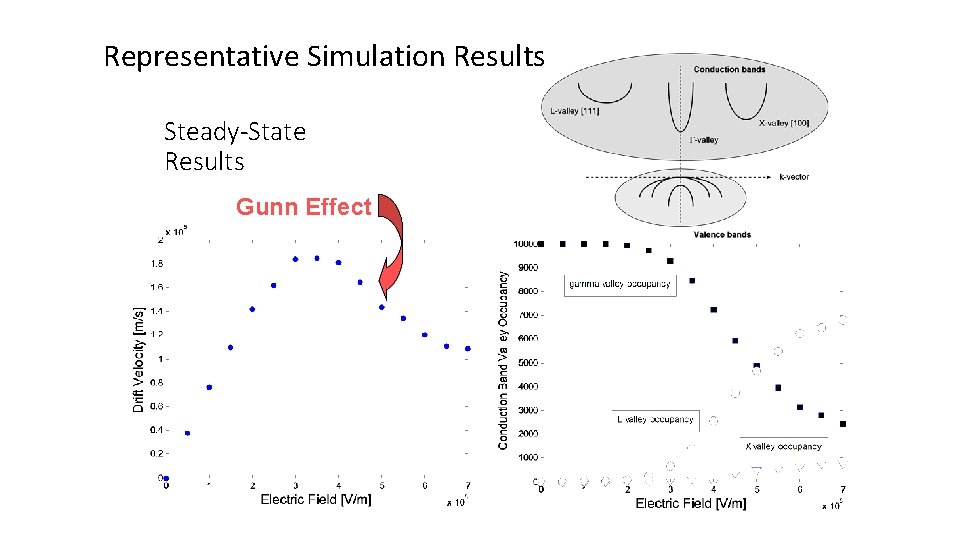
Representative Simulation Results Steady-State Results Gunn Effect

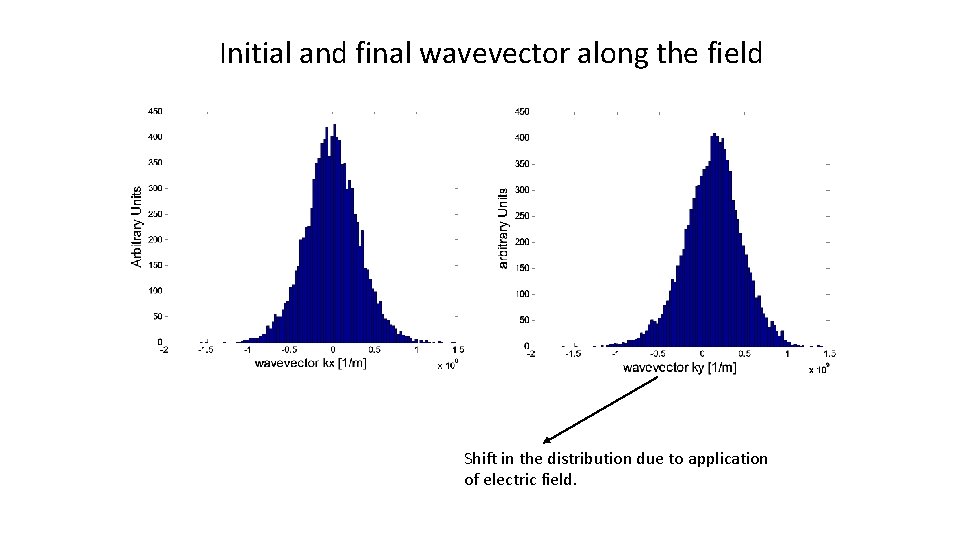
Initial and final wavevector along the field Shift in the distribution due to application of electric field.

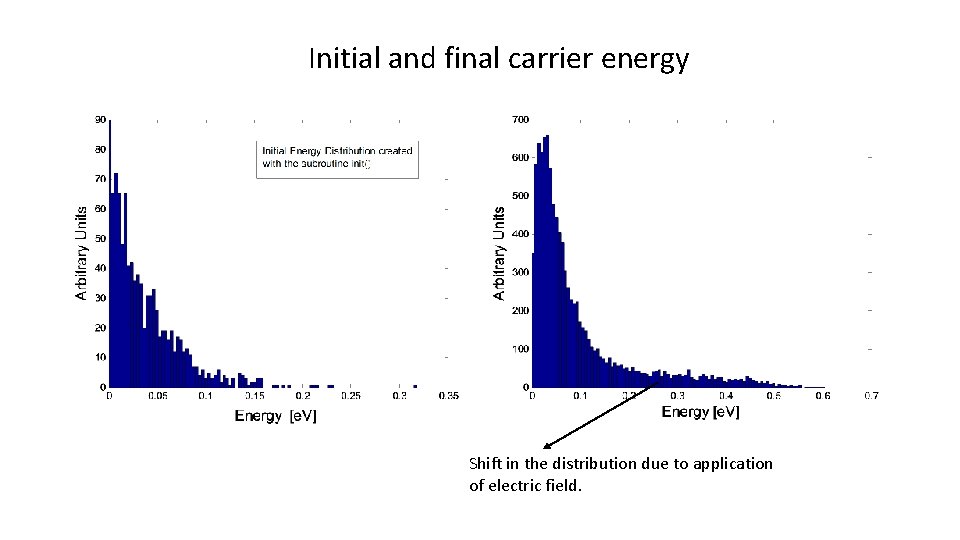
Initial and final carrier energy Shift in the distribution due to application of electric field.

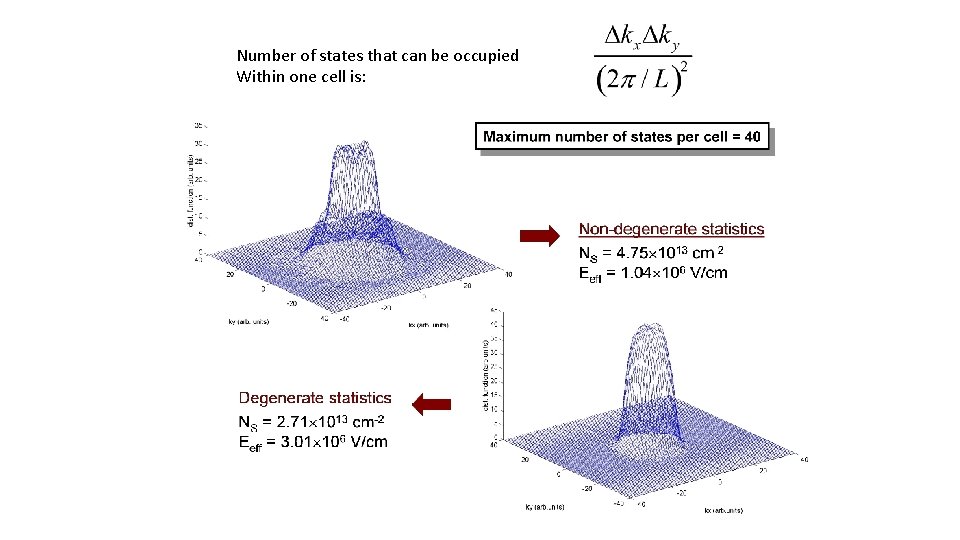
Inclusion of the Pauli Exclusion Principle v The influence of the final state on the scattering rate is important at low temperatures and high carrier densities. v This effect may be included via a self-scattering rejection method (Bosi and Jacoboni, J. Phys. C 9, 315 (1976); Lugli and Ferry, IEEE Trans. Elec. Dev. 32, 2431 (1985)). v The electron (hole) distribution function f(kx, ky, kz) is updated in k-space (on a 2 D or a 3 D grid). v Once the final state has been selected, a new random number is generated: v If , then self-scattering is assumed to occur with no change of momentum or energy v If , then accept the scattering event

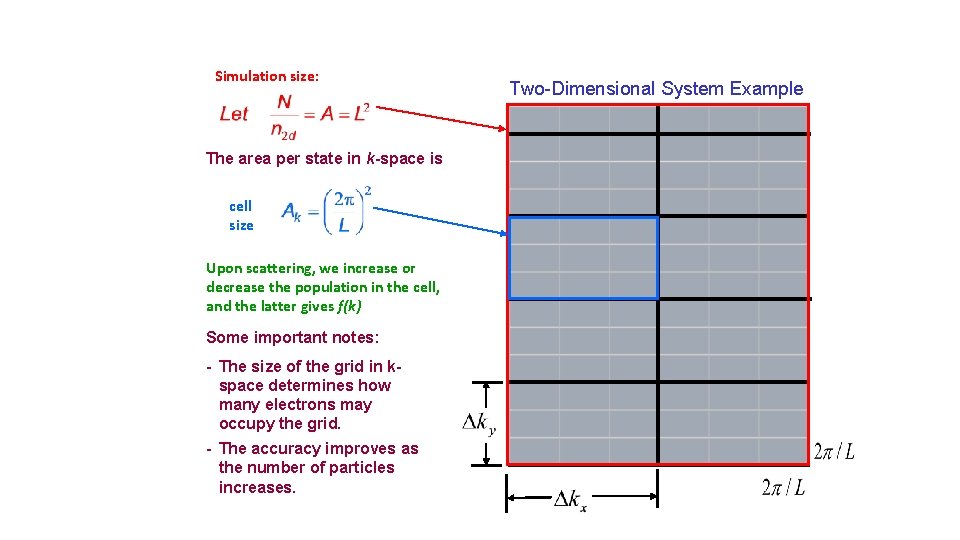
Simulation size: The area per state in k-space is cell size Upon scattering, we increase or decrease the population in the cell, and the latter gives f(k) Some important notes: - The size of the grid in kspace determines how many electrons may occupy the grid. - The accuracy improves as the number of particles increases. Two-Dimensional System Example

Number of states that can be occupied Within one cell is:

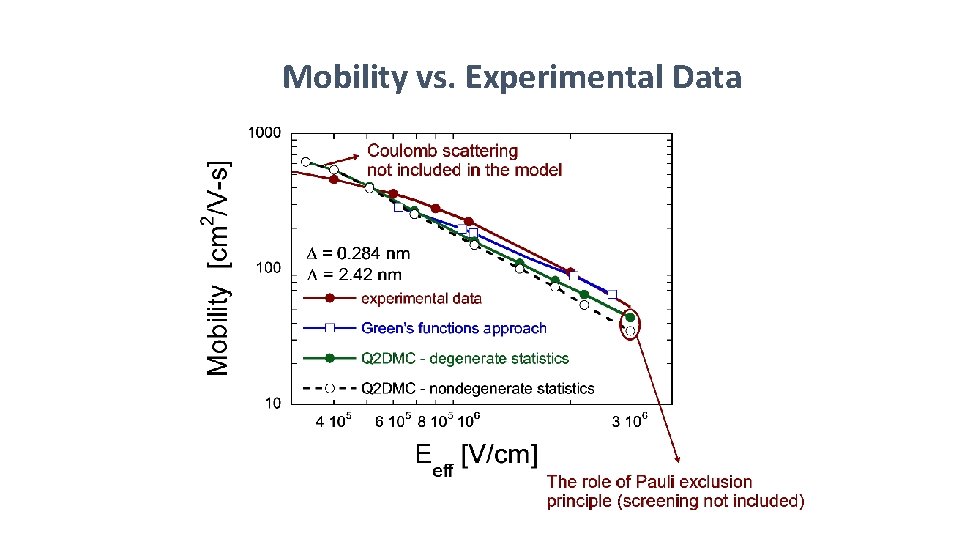
Mobility vs. Experimental Data

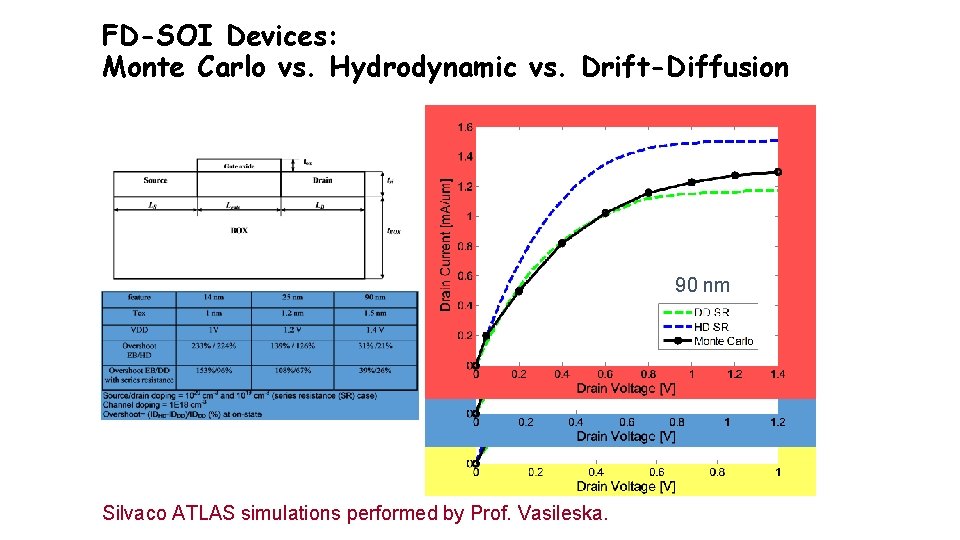
Modeling of SOI Devices Monte Carlo Particle Based Device Simulator • When modeling SOI devices lattice heating effects has to be accounted for • In what follows we discuss the following: • Comparison of the Monte Carlo, Hydrodynamic and Drift-Diffusion results of Fully-Depleted SOI Device Structures* • Impact of self-heating effects on the operation of the same generations of Fully-Depleted SOI Devices COMPUTEL

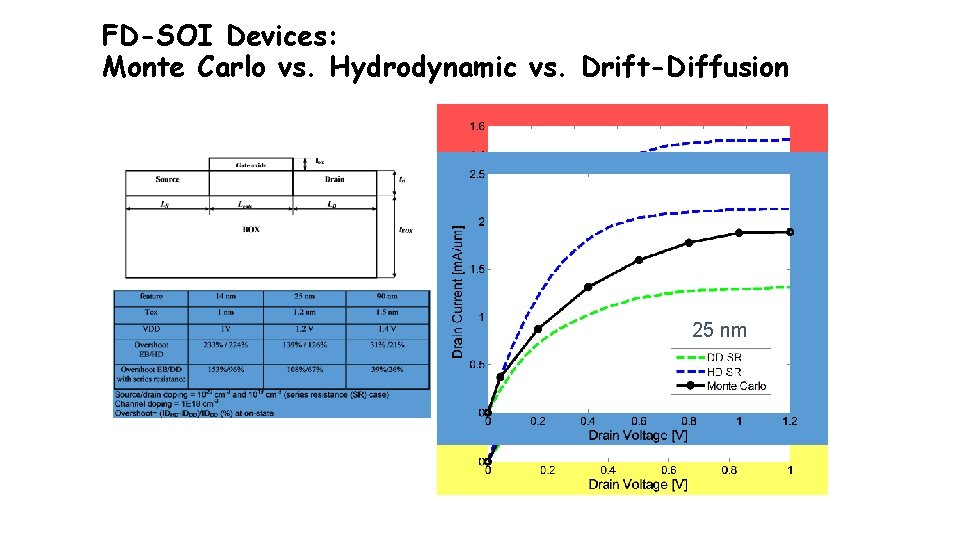
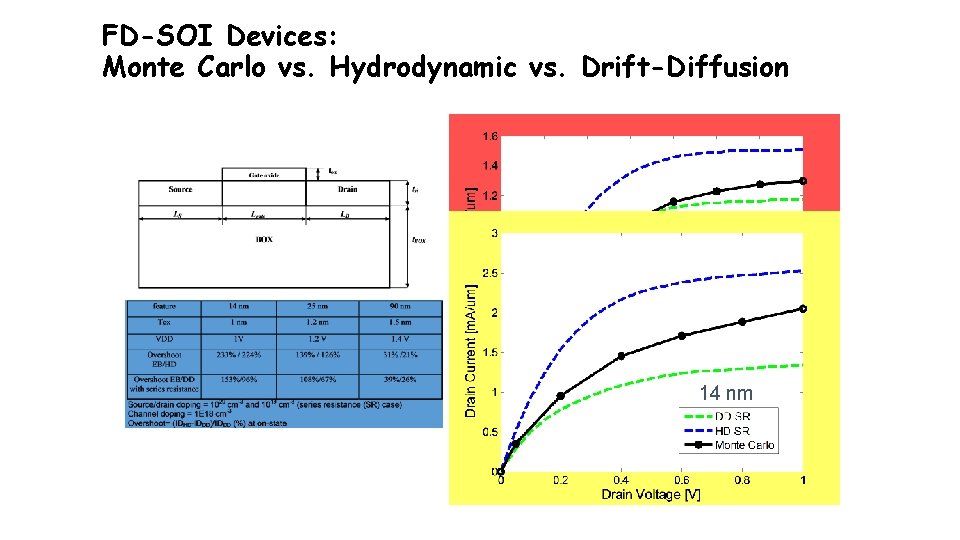
FD-SOI Devices: Monte Carlo vs. Hydrodynamic vs. Drift-Diffusion 90 nm Silvaco ATLAS simulations performed by Prof. Vasileska.

FD-SOI Devices: Monte Carlo vs. Hydrodynamic vs. Drift-Diffusion 25 nm

FD-SOI Devices: Monte Carlo vs. Hydrodynamic vs. Drift-Diffusion 14 nm

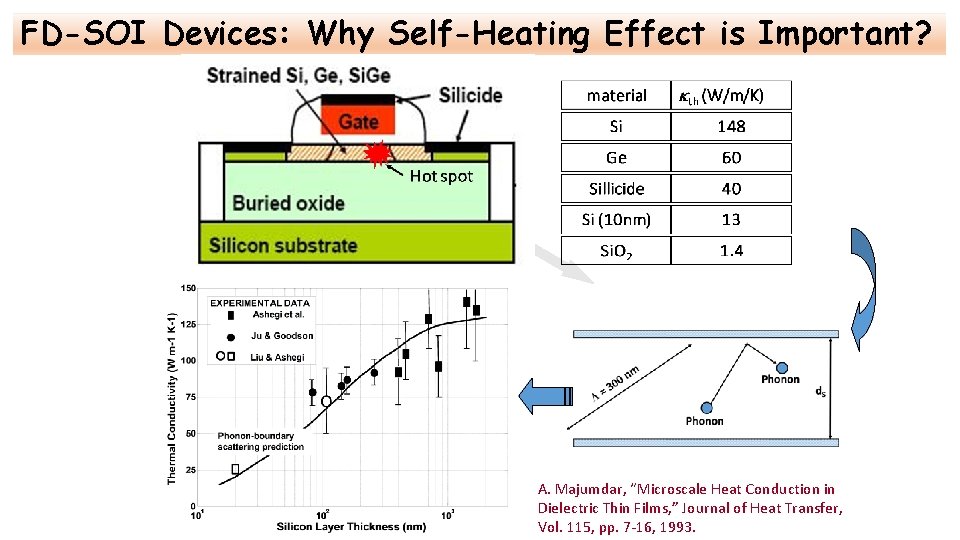
FD-SOI Devices: Why Self-Heating Effect is Important? A. Majumdar, “Microscale Heat Conduction in Dielectric Thin Films, ” Journal of Heat Transfer, Vol. 115, pp. 7 -16, 1993.

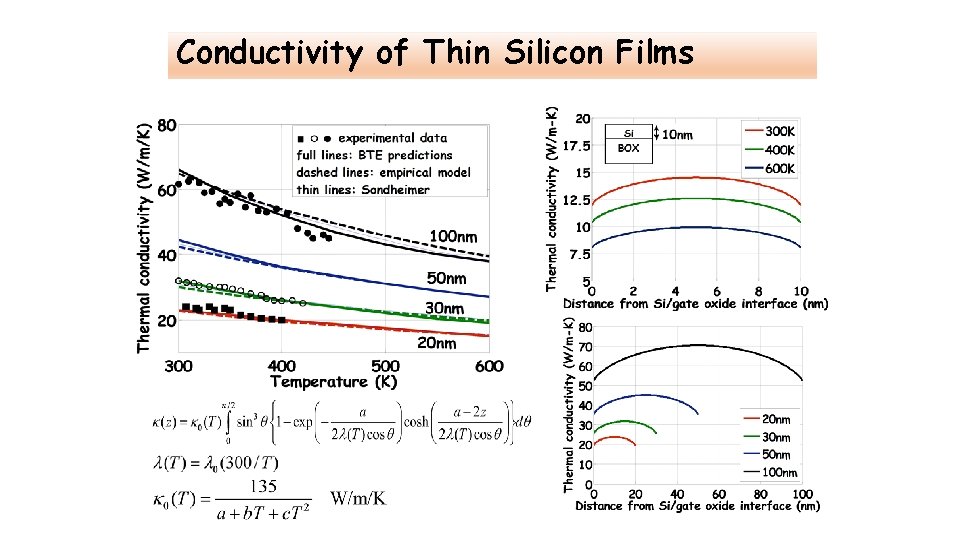
Conductivity of Thin Silicon Films

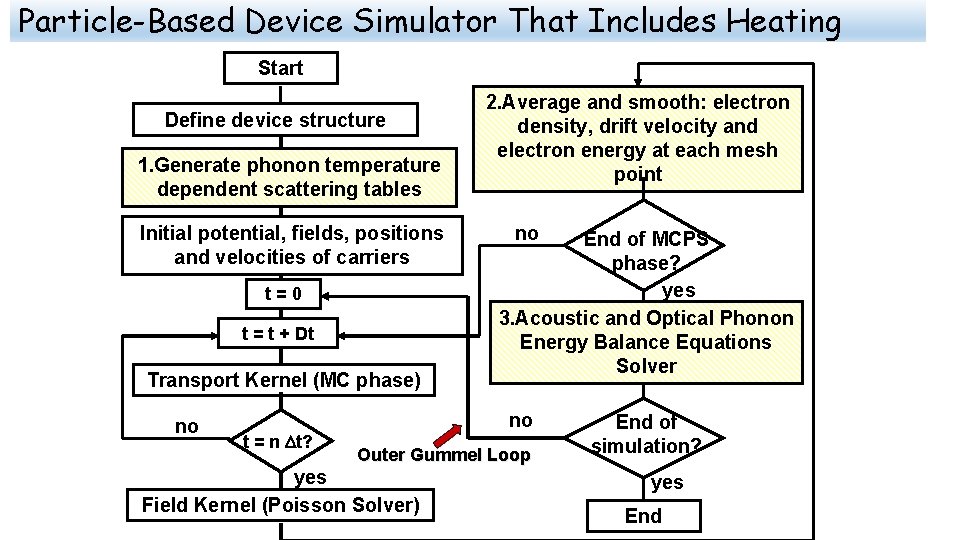
Particle-Based Device Simulator That Includes Heating Start Define device structure 1. Generate phonon temperature dependent scattering tables Initial potential, fields, positions and velocities of carriers t=0 t = t + Dt Transport Kernel (MC phase) no t = n Dt? 2. Average and smooth: electron density, drift velocity and electron energy at each mesh point no End of MCPS phase? yes 3. Acoustic and Optical Phonon Energy Balance Equations Solver no Outer Gummel Loop yes Field Kernel (Poisson Solver) End of simulation? yes End

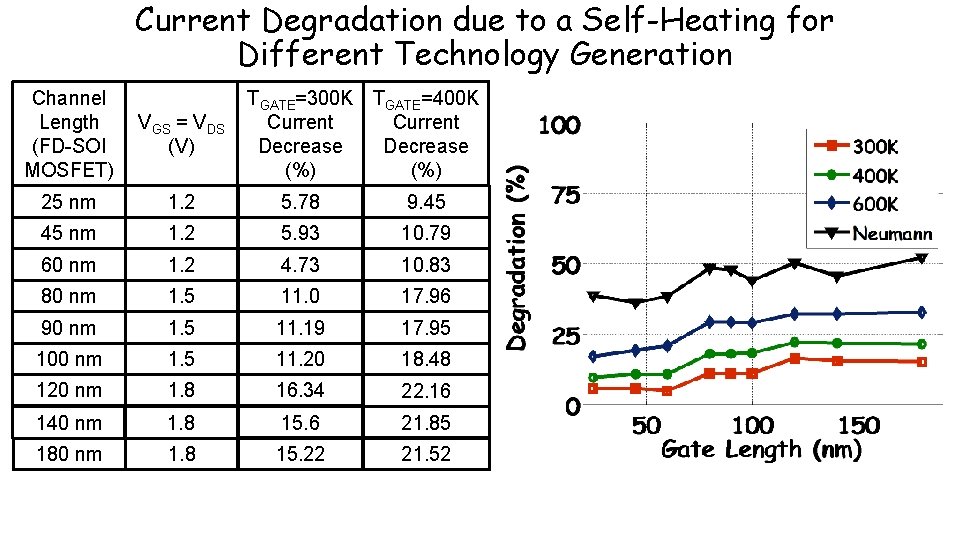
Current Degradation due to a Self-Heating for Different Technology Generation TGATE=300 K TGATE=400 K Current Decrease (%) Channel Length (FD-SOI MOSFET) VGS = VDS (V) 25 nm 1. 2 5. 78 9. 45 45 nm 1. 2 5. 93 10. 79 60 nm 1. 2 4. 73 10. 83 80 nm 1. 5 11. 0 17. 96 90 nm 1. 5 11. 19 17. 95 100 nm 1. 5 11. 20 18. 48 120 nm 1. 8 16. 34 22. 16 140 nm 1. 8 15. 6 21. 85 180 nm 1. 8 15. 22 21. 52

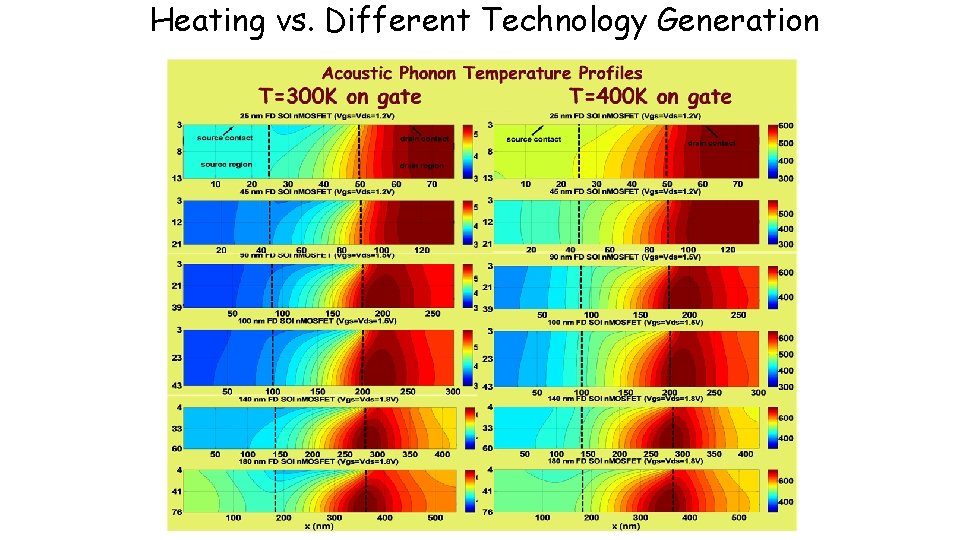
Heating vs. Different Technology Generation