Sts Cyril and Methodius University Skopje FACULTY OF

Sts. Cyril and Methodius University - Skopje FACULTY OF ELECTRICAL ENGINEERING AND INFORMATION TECHNOLOGIIES Semiconductor Device Modeling Lecture 5. Drift-Diffusion Equations NUMERICAL SOLUTION 1. Gummel’s Iteration Method 2. Newton’s Method 3. Time-Dependent Simulation 4. Scharfetter-Gummel Approximation prepared by Katerina Raleva and Dragica Vasileska Knowledge Alliance 562206 -EPP-1 -2015 -1 -BG-EPPKA 2 -KA Micro-Electronics Cloud Alliance (MECA)

Drift Diffusion Equations Poisson Equation Continuity Equations Current Density Equations

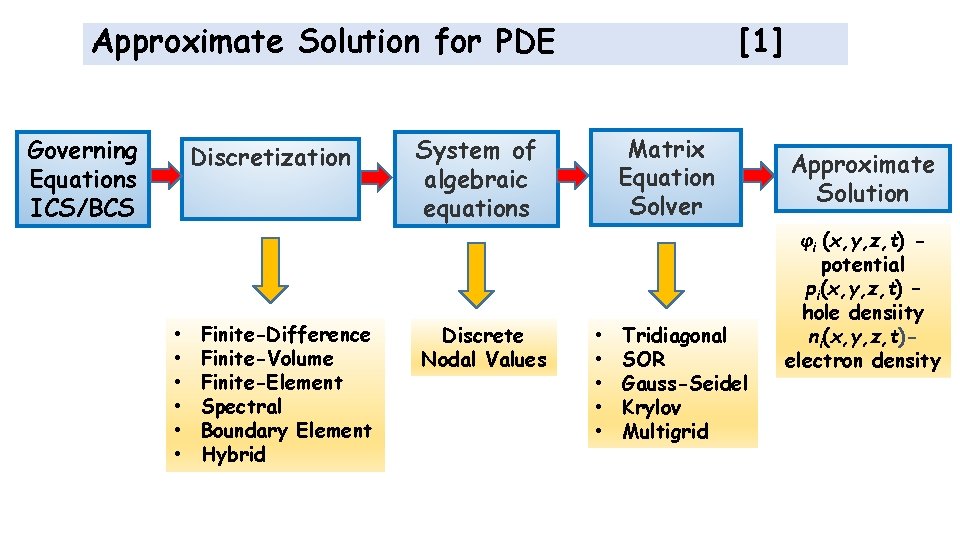
Approximate Solution for PDE Governing Equations ICS/BCS Discretization • • • Finite-Difference Finite-Volume Finite-Element Spectral Boundary Element Hybrid [1] Matrix Equation Solver System of algebraic equations Discrete Nodal Values • • • Tridiagonal SOR Gauss-Seidel Krylov Multigrid Approximate Solution φi (x, y, z, t) potential pi(x, y, z, t) – hole densiity ni(x, y, z, t)electron density

Approximate Solution for PDE – Discretization 1 2 3 Finite differences Finite volumes Finite elements [2] - time-dependent PDEs - Maxwell’s equations robust, simple concept, easy to parallelize, regular grids, explicit method - time-dependent PDEs robust, simple concept, irregular grids, explicit method - static and time-dependent PDEs - all problems implicit approach, matrix inversion, well founded, irregular grids, more complex algorithms, engineering problems

Approximate Solution for PDE – Discretization Finite Difference Method Common definitions of the derivative of f(x): These are all correct definitions in the limit dx 0. But we want dx to remain FINITE [3]

Approximate Solution for PDE – Discretization Finite Difference Method The equivalent approximations of the derivatives are: forward difference backward difference centered difference [4]

Approximate Solution for PDE – Discretization Finite Difference Method [5] How good are the FD approximations? Taylor series are expansions of a function f(x) for some finite distance dx to f(x+dx): What happens, if we use this expression for ? . . . that leads to :

Approximate Solution for PDE – Discretization Finite Difference Method [6] - Taylor Series (with forward formulation) The error of the first derivative using the forward formulation is of order dx.

Approximate Solution for PDE – Discretization Finite Difference Method [7] - Taylor Series (with centered formulation) . . . with the centered formulation we get: The error of the first derivative using the centered approximation is of order dx 2. This is an important results: it DOES matter which formulation we use. The centered scheme is more accurate! accurate

Approximate Solution for PDE – Discretization Finite Difference Method Second Derivative According to the well-known expansion, and Upon adding these expansions, [8]

Approximate Solution for PDE – Discretization Finite Difference Method [9] Second Derivative (cont’d) where O( x)4 is the error introduced by truncating the series. We say that this error is of the order ( x)4 or simply O( x)4. Therefore, O( x)4 represents terms that are not greater than ( x)4. Assuming that these terms are negligible,

Approximate Solution for PDE – Discretization Finite Difference Method FIRST DERIVATIVE SECOND DERIVATIVE Summary of Results [10]

Approximate Solution for PDE – Discretization Finite Difference Method - APPLICATION Application of Finite Difference Method to the Solution of: - 1 D Poisson Equation - 1 D Continuity Equation [11]

Approximate Solution for PDE – Poisson Equation How to solve it? STEP 1: LINEARIZATION STEP 2: DISCRETIZATION STEP 3: STEP 4: One has to apply proper boundary conditions: -Dirichlet vs Neumann -Treatment of the Ohmic Contacts Needs to be solved numerically: -Direct Methods -Iterative Methods for Solution of Sparse Matrix Problem

Approximate Solution for PDE – Poisson Equation [1] STEP 1: Linearization of the Poisson Equation The 1 D Poisson equation is of the form:

Approximate Solution for PDE – Poisson Equation [2] STEP 1: Linearization of the Poisson Equation (cont’d) [1] What are we solving for? Ec EF Ei Ev

Approximate Solution for PDE – Poisson Equation [3] STEP 1: Linearization of the Poisson Equation (cont’d) [3] Define: φnew => φold + d

Approximate Solution for PDE – Poisson Equation [4] STEP 1: Linearization of the Poisson Equation (cont’d) [4] Renormalized Form: LD=sqrt(qni/εVT)

Approximate Solution for PDE – Poisson Equation [5] STEP 2: Discretization of the linearized Poisson Equation Finite Difference Representation Equilibrium: n and p calculated using appropriate transport kernel. Non-Equilibrium: (In DD model n and p are solutions of the corresponding continuity equations).

Approximate Solution for PDE – Poisson Equation [6] STEP 3: Boundary Conditions for the Poisson Equation • Dirichlet Boundary Conditions at the Ohmic Contacts • Neumann Boundary Conditions at the artificial boundaries

Approximate Solution for PDE – Poisson Equation [7] STEP 3: Boundary Conditions for the Poisson Equation (cont’d) [1] Dirichlet Boundary Conditions at the Ohmic Contacts • a 5 = 0 • b 5 = 1 • c 5 = 0 • f 5 = build-in + Vapplied

Approximate Solution for PDE – Poisson Equation [8] STEP 3: Boundary Conditions for the Poisson Equation (cont’d) [1] Neumann Boundary Conditions at Artificial Boundaries • a 0 = 0 • c 0 = 2 c 0

Approximate Solution for PDE – Poisson Equation [9] 1 D, Finite-Difference Discretization of the Poisson Equation - Example The resultant finite difference equations can be represented in a matrix form A∙u=f, where: A=

Approximate Solution for PDE – Poisson Equation [10] 2 D, Finite-Difference Discretization of the Poisson Equation - Example In 2 D, finite-difference discretization of the Poisson equation leads to a FIVE POINT STENCIL:

Approximate Solution for PDE – Poisson Equation [11] 2 D, Finite-Difference Discretization of the Poisson Equation – Example (cont’d)

Approximate Solution for PDE – Continuity Equations • Have to be discretized properly • Have to apply proper boundary conditions • Have to be solved numerically using: • Direct methods • Iterative methods for sparse matrices

Scharfetter - Gummel Discretization of the Continuity Equation Assumptions: • Electron density varies exponentially between node points • Proper calculation of the Bernoulli function is essential function Ber = berfun(x) flag_sum = 0; if(x>1 e-10) Ber = x*exp(-x)/(1 -exp(-x)); elseif(x < abs(x) > 1 e-10) Ber = x/(exp(x)-1); elseif(x == 0) Ber = 1; else temp_term = 1; sum = temp_term; i = 0; while(~flag_sum) i = i + 1; temp_term = temp_term*x/(i+1); if( abs(temp_term) < 1 e-14) flag_sum = 1; else sum = sum + temp_term; end Ber = 1/sum; end

Sharfetter - Gummel Discretized Continuity Equations

Approximate Solution for PDE – Continuity Equations Boundary Conditions for the Charge Density • At the ohmic contacts, charge neutrality is assumed at the boundaries: p - n + ND – NA = 0 and np = ni 2 • an 5 = ap 5 = 0 • bn 5 = bp 5 = 1 • cn 5 = cp 5 = 0 • Gn 5 = n 0, Gp 5 = p 0

Components of numerical methods (Solution of linear equation systems, introduction) • The result of the discretization using either Finite-Difference or Finite-Volume, is a system of algebraic equations, which are linear or non-linear • For non-linear case, the system must be solved using iterative methods, i. e. initial guess iterate converged results obtained. • The matrices derived from partial differential equations are always sparse with the non-zero elements of the matrices lie on a small number of well-defined diagonals.

LU Decomposition Method

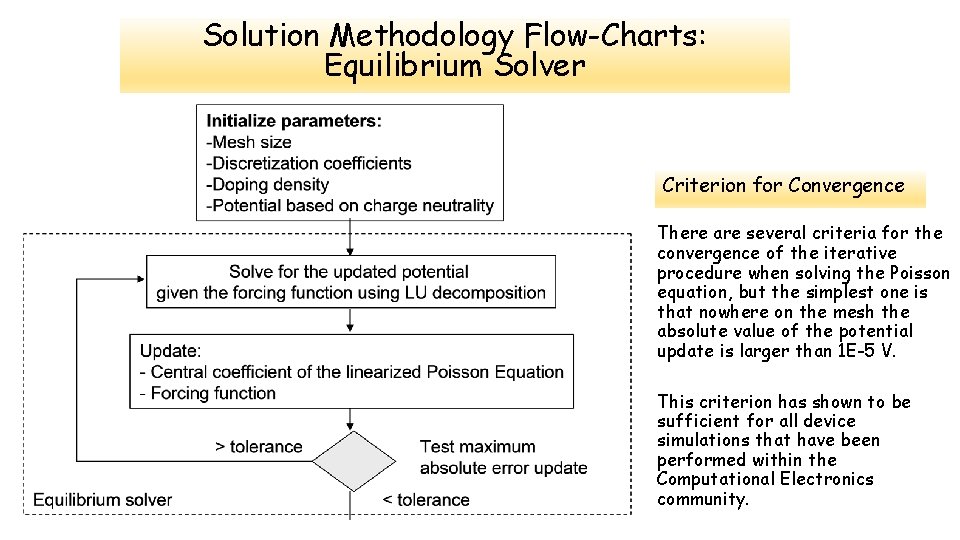
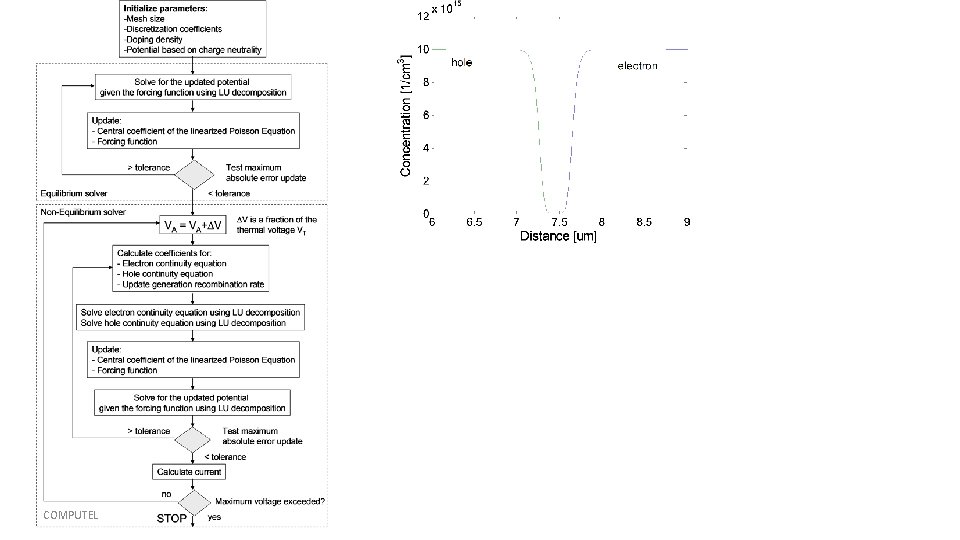
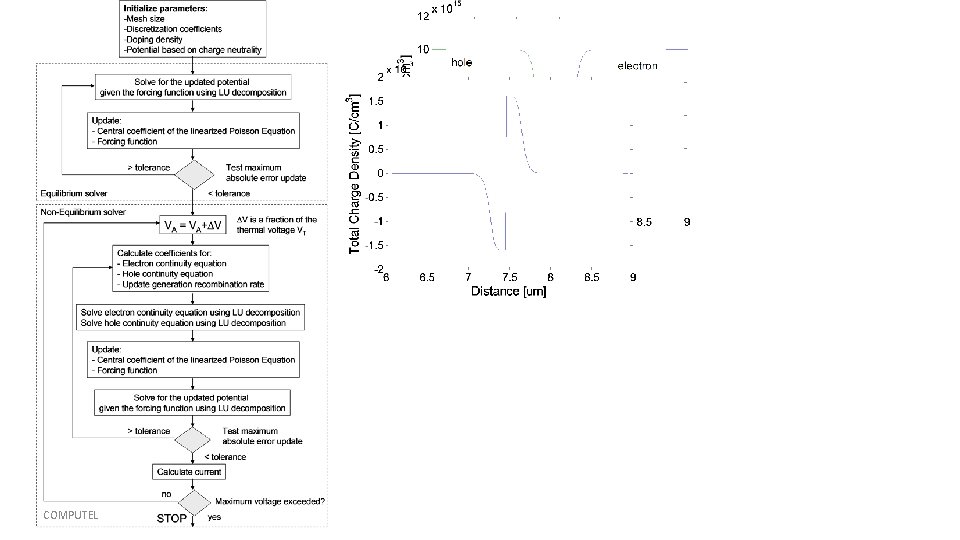
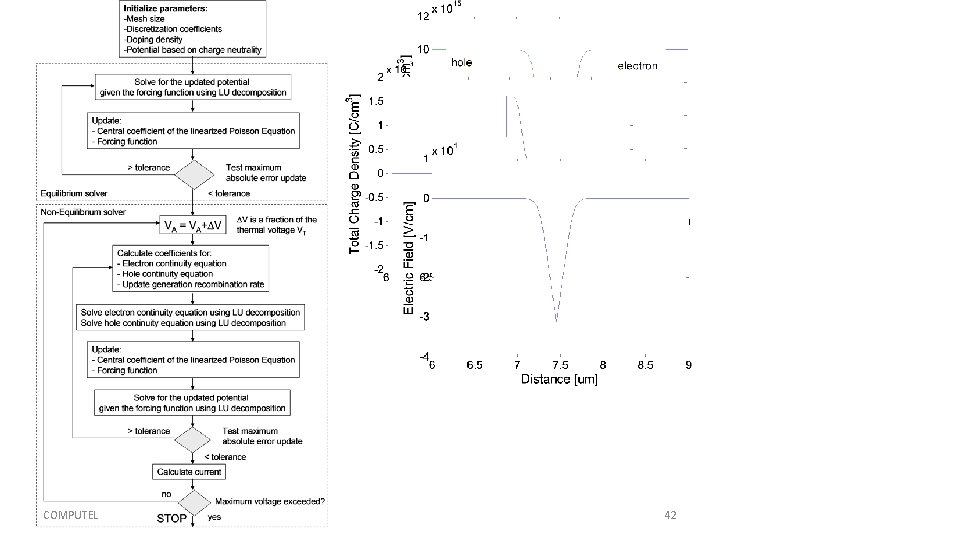
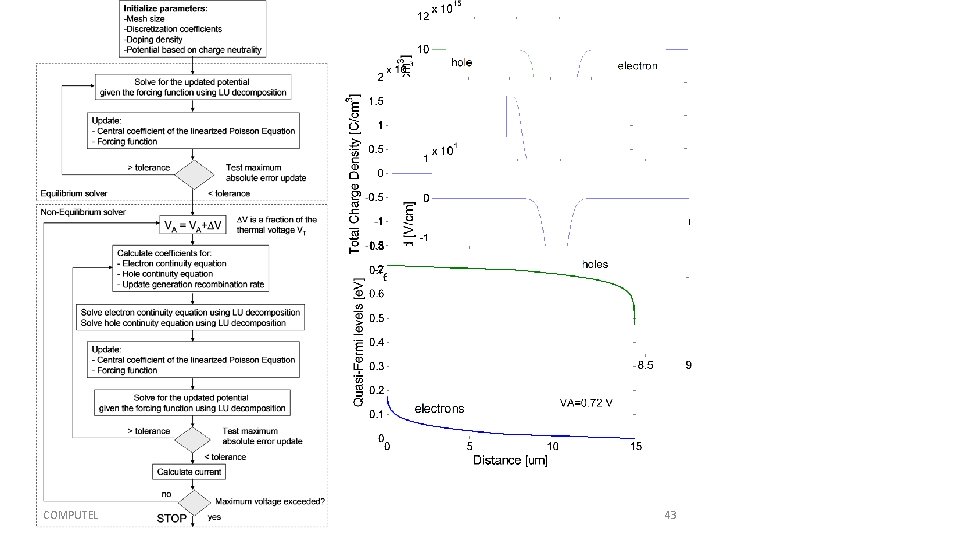
Solution Methodology Flow-Charts: Equilibrium Solver Criterion for Convergence There are several criteria for the convergence of the iterative procedure when solving the Poisson equation, but the simplest one is that nowhere on the mesh the absolute value of the potential update is larger than 1 E-5 V. This criterion has shown to be sufficient for all device simulations that have been performed within the Computational Electronics community.

Solving the Coupled Set of Equations • Gummel’s Scheme • Solves the constitutive equations in a sequential manner. • Good for small coupling between the equations – low bias conditions. • Densities in the generation/recombination processes included in the model are updated after one Gummel cycle is complete which comprises one solution of the Poisson and one solution of the electron and hole continuity equations in a sequential manner.

Solving the Coupled Set of Equations (cont’d) • Newton Method • Solves all constituent equations simultaneously • Must be used when the equation set is strongly coupled • Gummel-Newton method - sometimes is the strategy to go • When convergence is poor, it is useful to get a good initial guess for the Newton solver by performing several Gummel cycles

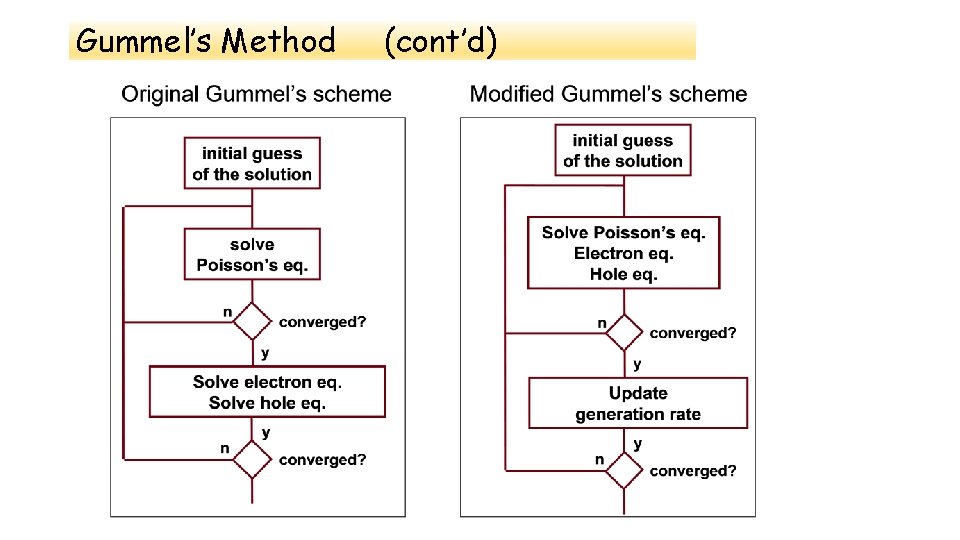
Gummel’s Method Gummel’s relaxation method, which solves the equations with the decoupled procedure, is used in the case of weak coupling: • Low current densities (leakage currents, subthreshold regime), where the concentration dependent diffusion term in the current continuity equation is dominant. • The electric field strength is lower than the avalanche threshold, so that the generation term is independent of V. • The mobility is nearly independent of E. The computational cost of the Gummel’s iteration is one matrix solution for each carrier type plus one iterative solution for the linearization of the Poisson Equation.

Gummel’s Method (cont’d)

Newton’s Method • The three equations that constitute the DD model, written in residual form are: • Starting from an initial guess, the corrections are calculated by solving:

Newton’s Method (cont’d)

Solution Methodology Flow-Charts: Non-Equilibrium solver

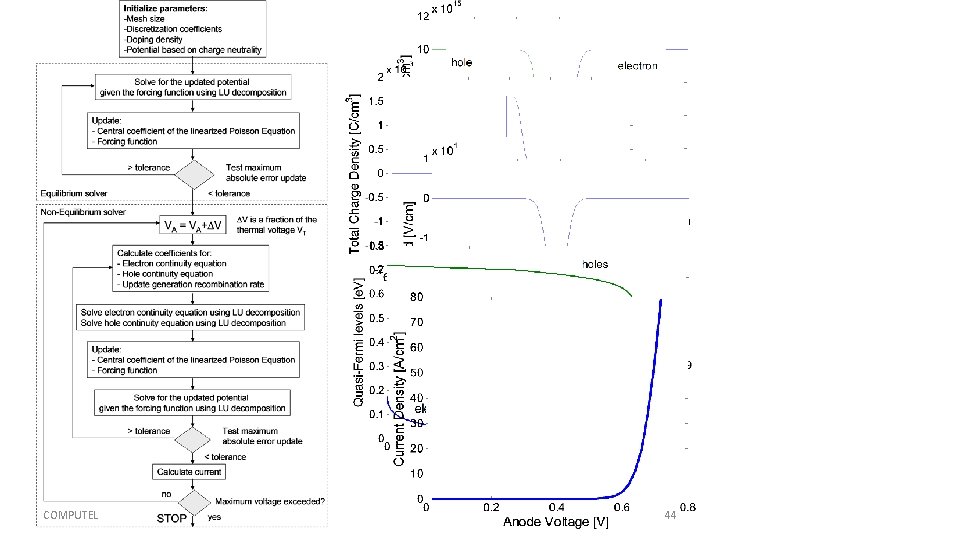
COMPUTEL

COMPUTEL

COMPUTEL 42

COMPUTEL 43

COMPUTEL 44

In which devices Drift-Diffusion Model can be used? • DD Model is good for devices operated at relatively small biases (up to velocity saturation in the channel). Solar cells, long channel MOSFETs, low-power devices • DD Model fails in nanoscale and high-power devices in which velocity overshoot plays significant role: Nano-transistors in which ballistic transport dominates the device behavior, high power devices