Sts Cyril and Methodius University Faculty of Natural

Sts Cyril and Methodius University Faculty of Natural Sciences and Mathematics Institute of Physics P. O. Box 162, 1000 Skopje, Macedonia DESYNCHRONIZATION OF SYSTEMS OF HINDMARSH-ROSE OSCILLATORS BY VARIABLE TIME-DELAY FEEDBACK A. Gjurchinovski 1, V. Urumov 1 and Z. Vasilkoski 2 1 Institute of Physics, Sts Cyril and Methodius University, Skopje, Macedonia 2 Northeastern University, Boston, USA E-Mail: urumov@pmf. ukim. mk International Conference in Memory of Academician Matey Mateev – Sofia , 2011

CONTENTS I. Introduction 1. - Time-delay feedback control 2. - Variable-delay feedback control II. Stability of fixed points, periodic orbits - Ordinary differential equations - Delay-differential equations - Fractional-order differential equations III. Desynchronisation in systems of coupled oscillators IV. Conclusions

INTRODUCTION Time-delayed feedback control - generalizations • • Pyragas 1992 – Feedback proportional to the distance between the current state and the state one period in the past (TDAS) Socolar, Sukow, Gauthier 1994 – Improvement of the Pyragas scheme by using information from many previous states of the system – commensurate delays (ETDAS) Schuster, Stemmler 1997 – Variable gain Ahlborn, Parlitz 2004 – Multiple delay feedback with incommensurate delays (MDFC) Distributed delays (electrical engineering) Variable delays (mechanical engineering) Rosenblum, Pikovsky 2004 – Desynchronization of systems of oscillators with constant delay feedback E. Schoell and H. G. Schuster, eds. , Handbook of chaos control 2 ed. (Wiley-VCH, Weinheim, 2008)

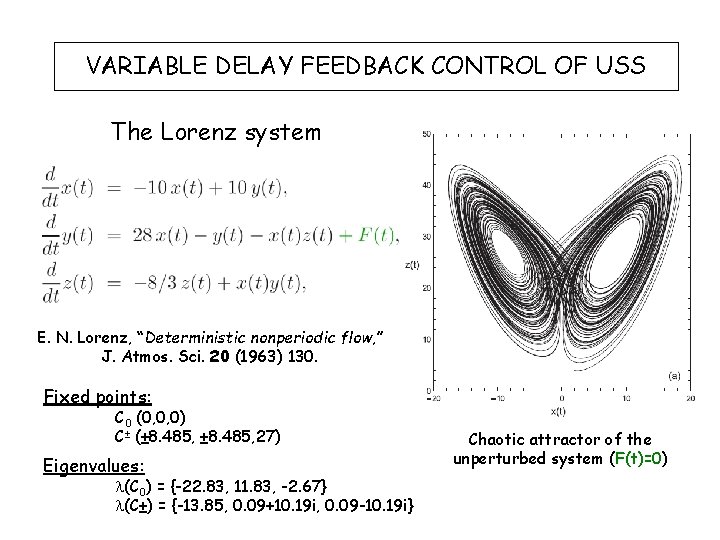
VARIABLE DELAY FEEDBACK CONTROL OF USS The Lorenz system E. N. Lorenz, “Deterministic nonperiodic flow, ” J. Atmos. Sci. 20 (1963) 130. Fixed points: C 0 (0, 0, 0) C± (± 8. 485, 27) Eigenvalues: l(C 0) = {-22. 83, 11. 83, -2. 67} l(C±) = {-13. 85, 0. 09+10. 19 i, 0. 09 -10. 19 i} Chaotic attractor of the unperturbed system (F(t)=0)

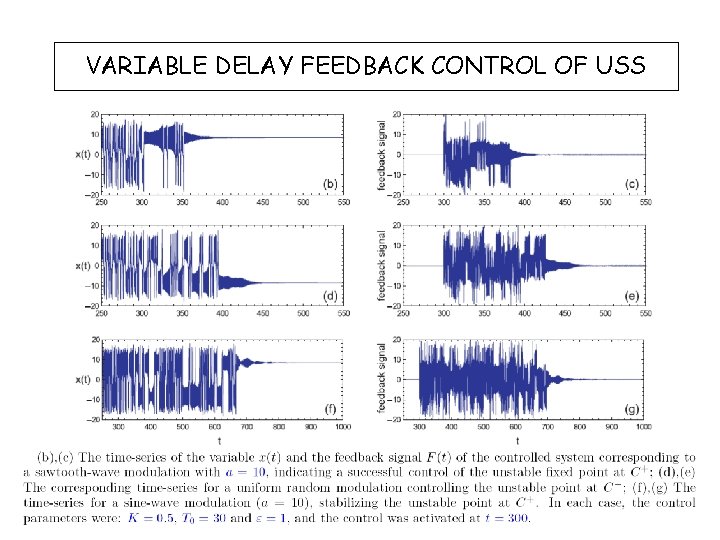
VARIABLE DELAY FEEDBACK CONTROL OF USS Pyragas control force: - noninvasive for USS and periodic orbits VDFC force: - piezoelements, noise - saw tooth wave: - random wave: - sine wave: A. Gjurchinovski and V. Urumov – Europhys. Lett. 84, 40013 (2008)

VARIABLE DELAY FEEDBACK CONTROL OF USS

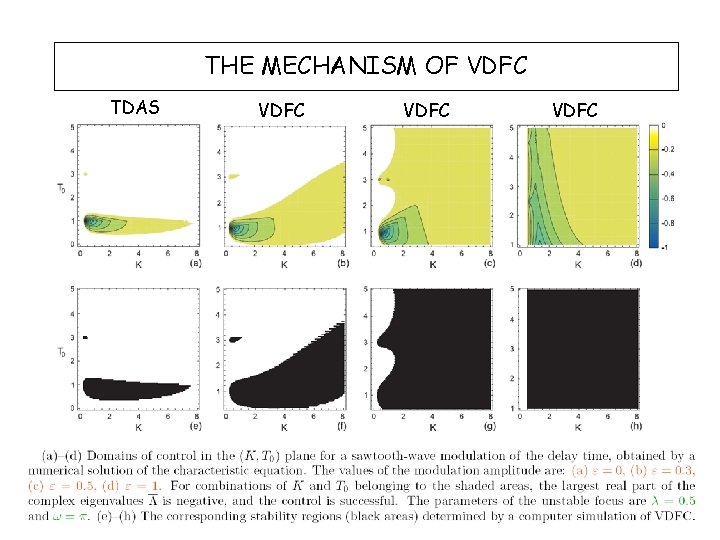
THE MECHANISM OF VDFC TDAS VDFC

STABILITY ANALYSIS - RDDE Retarded delay-differential equations Controlled RDDE system: u(t) – Pyragas-type feedback force with a variable time delay K T 2 f – feedback gain (strength of the feedback) – nominal delay value – periodic function with zero mean – amplitude of the modulation – frequency of the modulation A. Gjurchinovski, V. Urumov – Physical Review E 81, 016209 (2010)

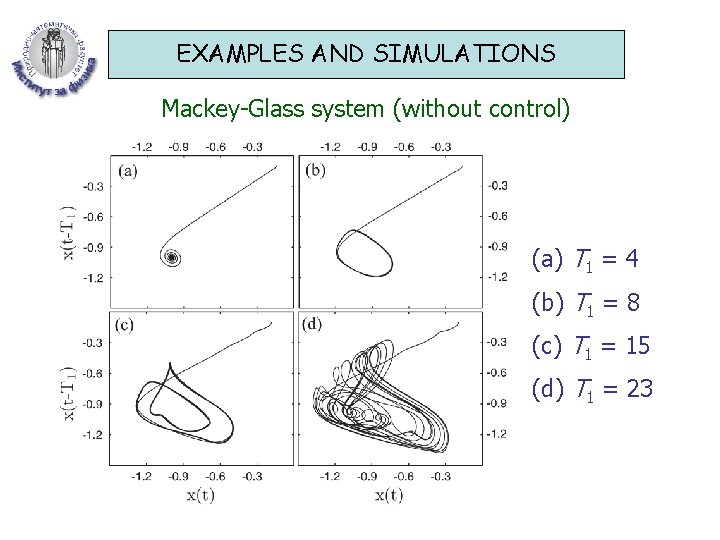
EXAMPLES AND SIMULATIONS Mackey-Glass system • A model for regeneration of blood cells in patients with leukemia M. C. Mackey and L. Glass, Science 197, 28 (1977). • M-G system under variable-delay feedback control: • For the typical values a = 0. 2, b = 0. 1 and c = 10, the fixed points of the freerunning system are: • • • x 1 = 0 – unstable for any T 1, cannot be stabilized by VDFC x 2 = +1 – stable for T 1 [0, 4. 7082) x 3 = -1 – stable for T 1 [0, 4. 7082)

EXAMPLES AND SIMULATIONS Mackey-Glass system (without control) (a) T 1 = 4 (b) T 1 = 8 (c) T 1 = 15 (d) T 1 = 23

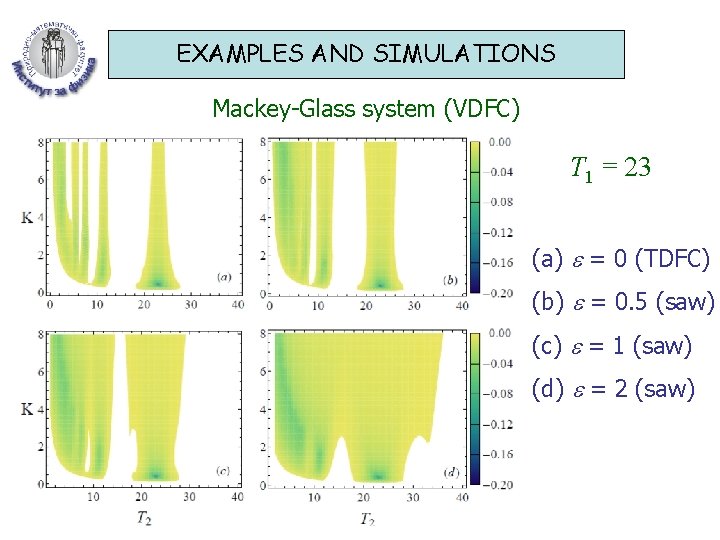
EXAMPLES AND SIMULATIONS Mackey-Glass system (VDFC) T 1 = 23 (a) = 0 (TDFC) (b) = 0. 5 (saw) (c) = 1 (saw) (d) = 2 (saw)

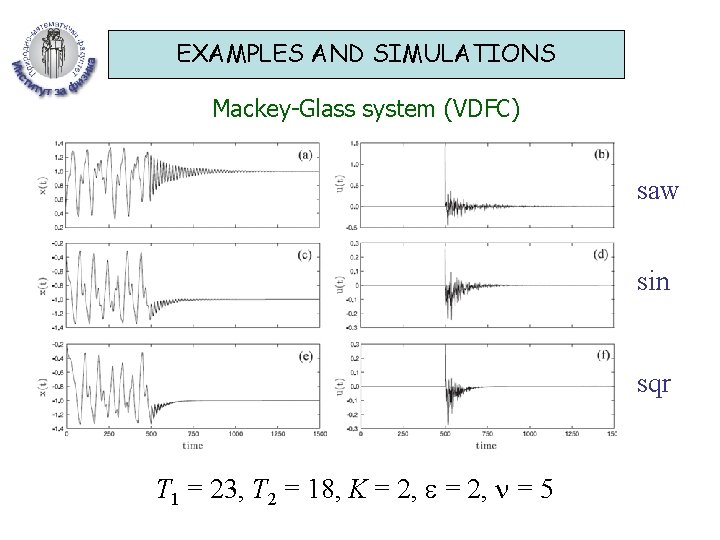
EXAMPLES AND SIMULATIONS Mackey-Glass system (VDFC) saw sin sqr T 1 = 23, T 2 = 18, K = 2, = 5

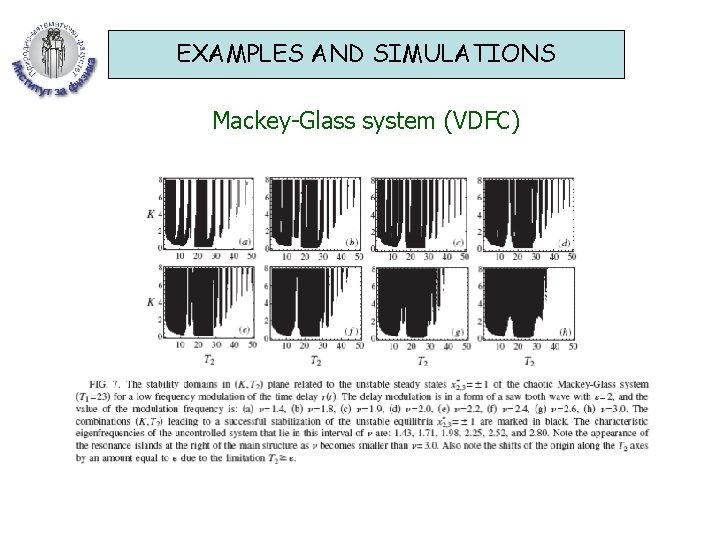
EXAMPLES AND SIMULATIONS Mackey-Glass system (VDFC)

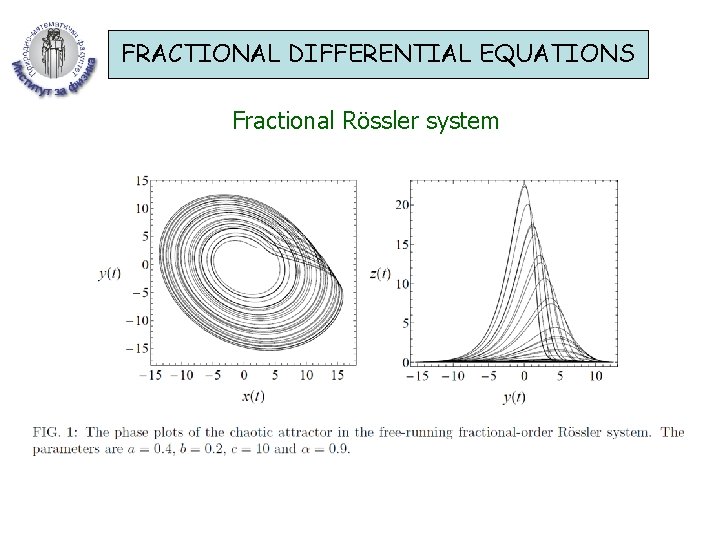
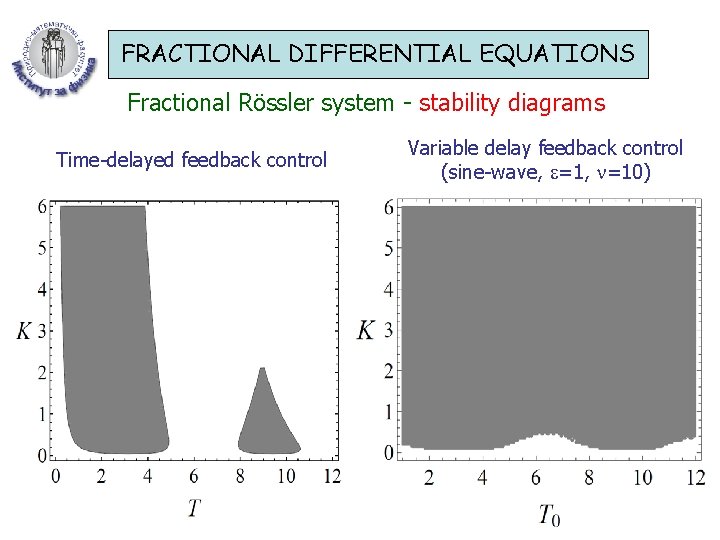
FRACTIONAL DIFFERENTIAL EQUATIONS Fractional Rössler system Caputo fractional-order derivative: A. Gjurchinovski, T. Sandev and V. Urumov – J. Phys. A 43, 445102 (2010)

FRACTIONAL DIFFERENTIAL EQUATIONS Fractional Rössler system

FRACTIONAL DIFFERENTIAL EQUATIONS Fractional Rössler system - stability diagrams Time-delayed feedback control Variable delay feedback control (sine-wave, =10)

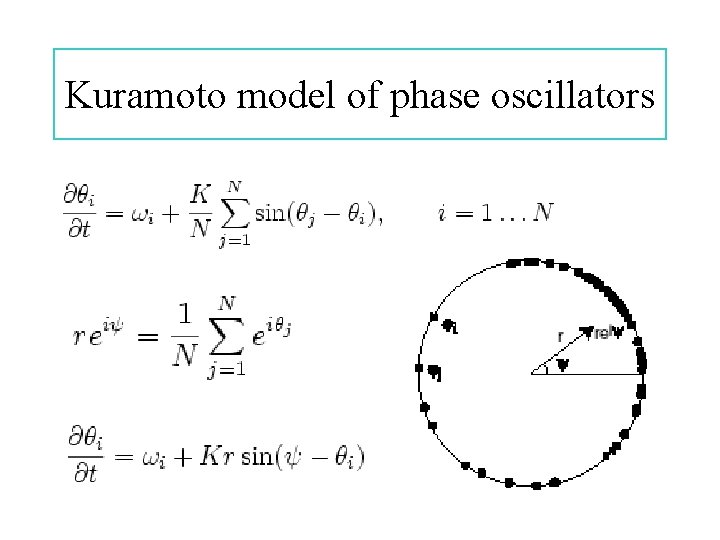
Kuramoto model of phase oscillators

Solution for the Kuramoto model (1975) solutions i

DEEP BRAIN STIMULATION • Delay - deliberately introduced to control pathological synchrony manifested in some diseases • Delay - due to signal propagation • Delay – due to self-feedback loop of neurovascular coupling in the brain

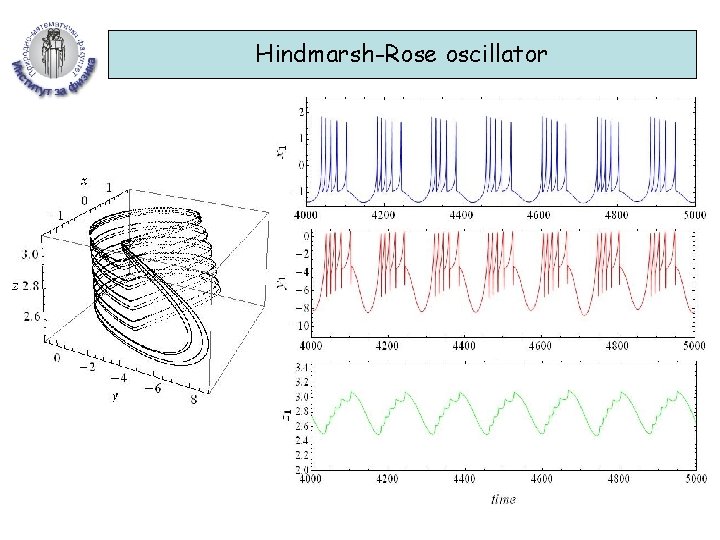
Hindmarsh-Rose oscillator

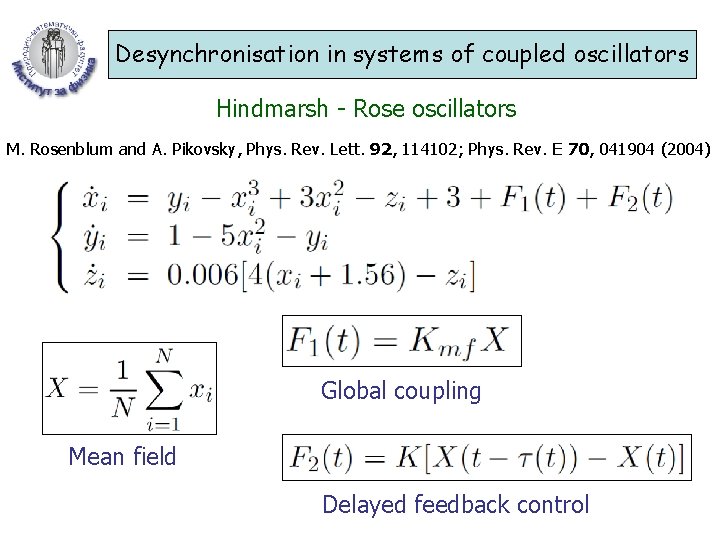
Desynchronisation in systems of coupled oscillators Hindmarsh - Rose oscillators M. Rosenblum and A. Pikovsky, Phys. Rev. Lett. 92, 114102; Phys. Rev. E 70, 041904 (2004) Global coupling Mean field Delayed feedback control

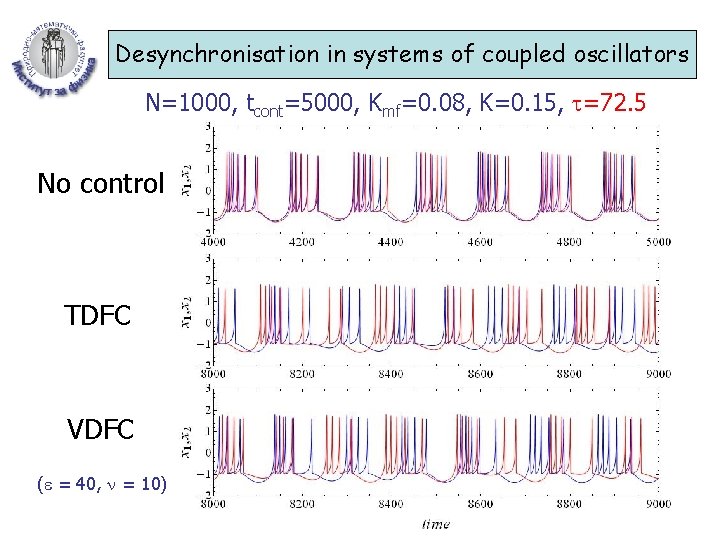
Desynchronisation in systems of coupled oscillators N=1000, tcont=5000, Kmf=0. 08, K=0. 15, =72. 5 No control TDFC VDFC ( = 40, = 10)

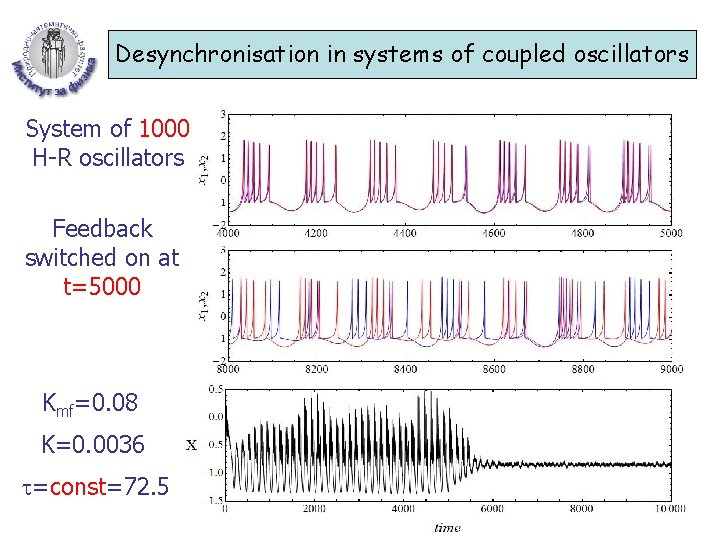
Desynchronisation in systems of coupled oscillators System of 1000 H-R oscillators Feedback switched on at t=5000 Kmf=0. 08 K=0. 0036 =const=72. 5

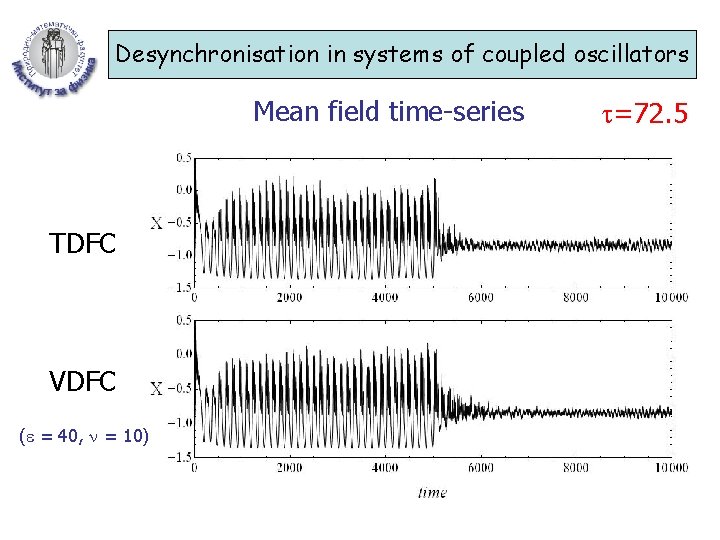
Desynchronisation in systems of coupled oscillators Mean field time-series TDFC VDFC ( = 40, = 10) =72. 5

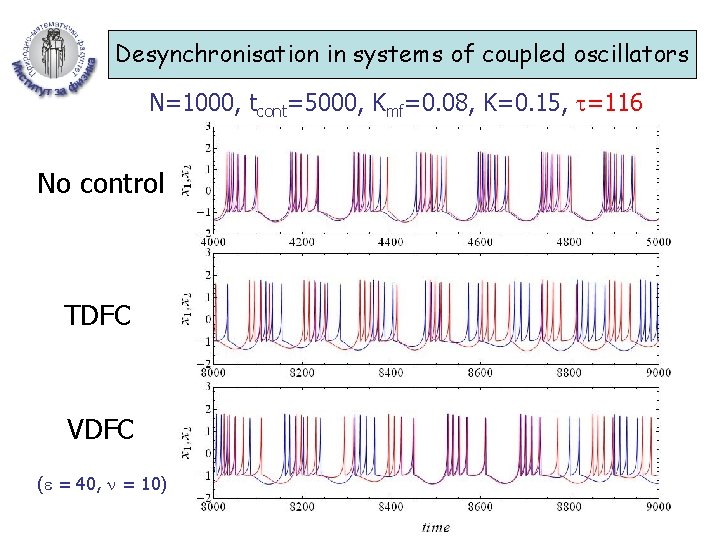
Desynchronisation in systems of coupled oscillators N=1000, tcont=5000, Kmf=0. 08, K=0. 15, =116 No control TDFC VDFC ( = 40, = 10)

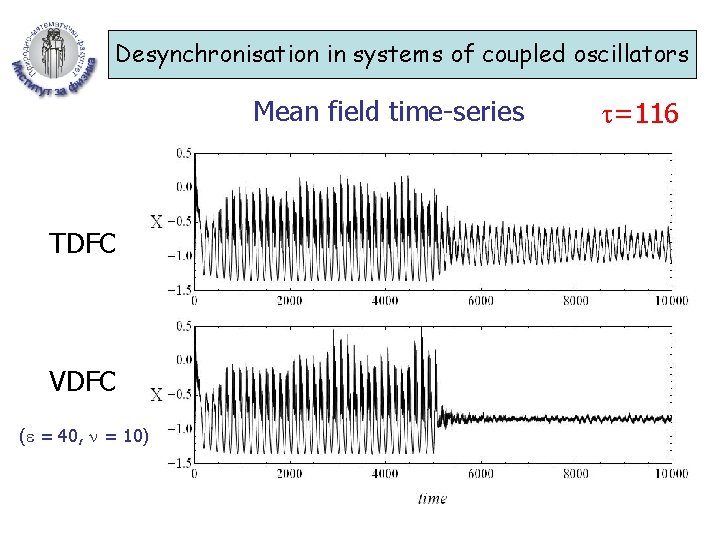
Desynchronisation in systems of coupled oscillators Mean field time-series TDFC VDFC ( = 40, = 10) =116

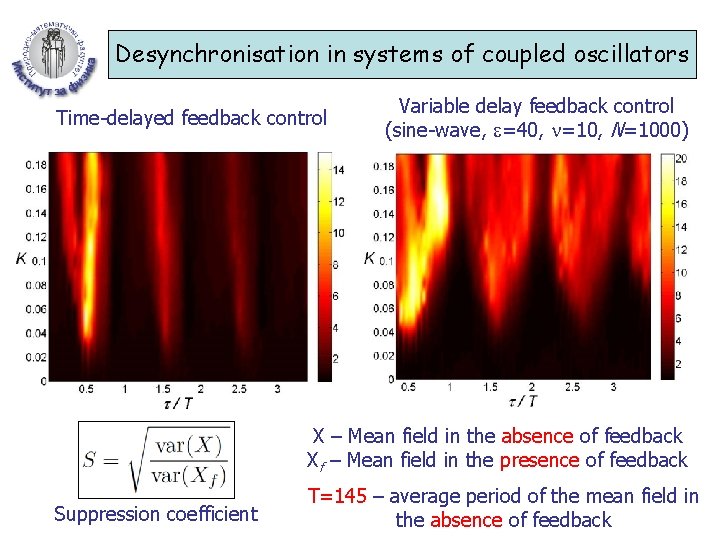
Desynchronisation in systems of coupled oscillators Time-delayed feedback control Variable delay feedback control (sine-wave, =40, =10, N=1000) X – Mean field in the absence of feedback Xf – Mean field in the presence of feedback Suppression coefficient T=145 – average period of the mean field in the absence of feedback

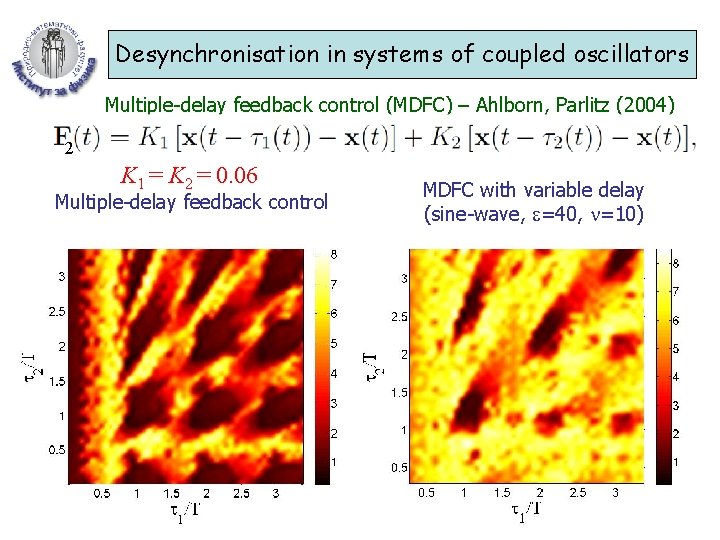
Desynchronisation in systems of coupled oscillators Multiple-delay feedback control (MDFC) – Ahlborn, Parlitz (2004) 2 K 1 = K 2 = 0. 06 Multiple-delay feedback control MDFC with variable delay (sine-wave, =40, =10)

CONCLUSIONS AND FUTURE PROSPECTS • Enlarged domain for stabilization of unstable steady states in systems of ordinary/delay/fractional differential equations in comparison with Pyragas method and its generalizations • Agreement between theory and simulations for large frequencies in the delay modulation • Variable delay feedback control provides increased robustness in achieving desynchronization in wider domain of parameter space in system of coupled Hindmarsh-Rose oscillators interacting through their mean field • The influence of variable-delay feedback in other systems (neutral DDE, PDE, networks, different oscillators, …) • Experimental verification