Sts Cyril and Methodius University Skopje FACULTY OF

Sts. Cyril and Methodius University - Skopje FACULTY OF ELECTRICAL ENGINEERING AND INFORMATION TECHNOLOGIIES Semiconductor Device Modeling Lecture 3. BOLTZMANN TRANSPORT EQUATION (BTE) 1. Introduction to BTE 2. Scattering Processes 3. Relaxation-Time Approximation (RTA) 4. Solving BTE in the RTA prepared by Katerina Raleva and Dragica Vasileska Knowledge Alliance 562206 -EPP-1 -2015 -1 -BG-EPPKA 2 -KA Micro-Electronics Cloud Alliance (MECA)

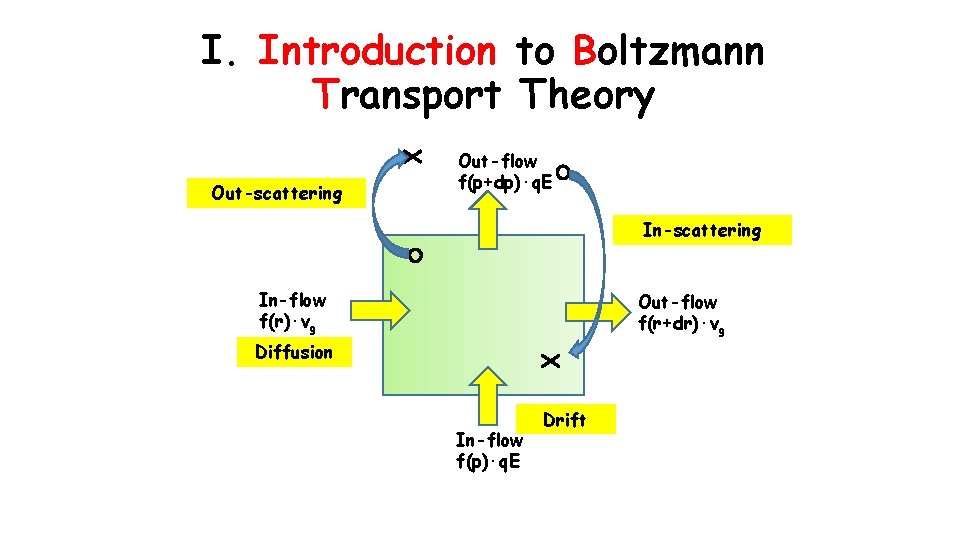
I. Introduction to Boltzmann Transport Theory Out-scattering Out-flow f(p+dp)∙q. E In-scattering In-flow f(r)∙vg Out-flow f(r+dr)∙vg Diffusion In-flow f(p)∙q. E Drift

Derivation of Boltzmann Transport Equation (BTE) [1] Kinetic theory: theory We need to derive an equation for the single particle distribution function f(v, r, t) (classical) which gives the probability of finding a particle with velocity between v and v+dv and in the region r to r+dr • We assume that v and r are given simultaneously which neglects quantum mechanical nature of particles. • f(v, r, t) allows us to calculate ensemble averages over velocity and space (particle density, current density, energy density, etc. ):

Derivation of Boltzmann Transport Equation (BTE) [2] • For this to give the proper average, f is normalized as follows: • To derive an equation of motion for f(v, r, t), it is somewhat easier to consider the particle density: where • The density n(v, r, t) should satisfy a continuity equation in the 6 D phase space defined by: x, y, z, vx, vy, vz -> independent variables

Derivation of Boltzmann Transport Equation (BTE) [3] • Consider a hyper-volume in phase space j(r, v, t) is the flux density j(r, v, t) ds is flux through hypersurface ds V S • Consider the particle balance through the hyper-volume V Time rate of change of # particles in V Leakage through S Time rate of change due to collisions Time rate of change due to G-R mechanisms

Derivation of Boltzmann Transport Equation (BTE) [4] • The flux density is written in terms of the time derivatives of the ‘position’ variables in 6 D: • Applying the divergence theorem in 6 D: where the divergence of j is:

Derivation of Boltzmann Transport Equation (BTE) [5] which is written more compactly as: • Particle balance is therefore: Normalizing, we get the classical form of the Boltzmann transport equation: First two terms on the rhs are the streaming terms

Derivation of Boltzmann Transport Equation (BTE) [6] • For Bloch electrons in a semiconductor, we could have considered a 6 D space x, y, z, kx, ky, kz where k is the wavevector and • The semi-classical BTE for transport of Bloch electrons is therefore:

Derivation of Boltzmann Transport Equation (BTE) [7] The semi-classical BTE for transport of Bloch electrons: p Out-flow f(p+dp)∙q. E Out-scattering In-scattering p+dp BTE is nothing more than a detailed balance of particle flow, or continuity equation, in 6 D phase space. In-flow f(r)∙vg Out-flow f(r+dr)∙vg Diffusion p In-flow f(p)∙q. E r Drift r r+dr

Boltzmann Transport Equation with Collision Integral [1] Assume instantaneous, single collisions which are independent of the driving force and take particles from k to k (out-scattering) or from k to k (in-scattering). Out-scattering In-scattering

Boltzmann Transport Equation with Collision Integral [2] (A) Out-Scattering the transition rate per particle from k to k Distribution function is: Take limit as t 0: where the last term in brackets accounts for the Pauli exclusions principle (degeneracy of the final state after scattering).

Boltzmann Transport Equation with Collision Integral [3] (B) In Scattering By an analogous argument, the rate of change of the distribution function due to in-scattering is: Total rate of change of f (r, k, t) around k is a sum over all possible initial and final states k : In-scattering Out-scattering

Boltzmann Transport Equation with Collision Integral [4] The sum over final states k may be converted to an integral due to the small volume of k-space associated with each state: The BTE becomes:

II. Scattering Processes [1] Free carriers (electrons and holes) interact with the crystal and with each other through a variety of scattering processes which relax the energy and momentum of the particle.

Scattering Processes [2] What contributes to ? The transition rate from initial state k to a final state k’ for a given scattering mechanism is given by Fermi’s Golden rule

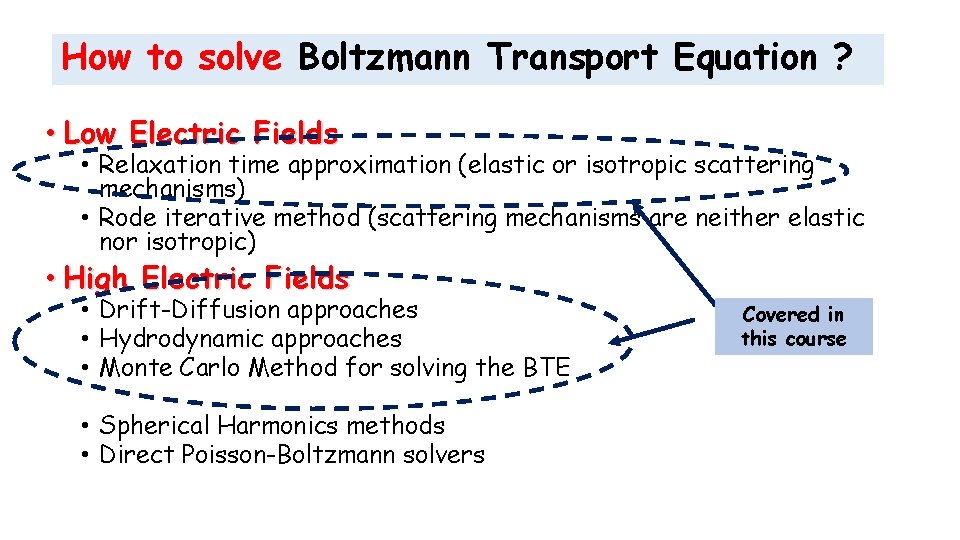
How to solve Boltzmann Transport Equation ? • Low Electric Fields • Relaxation time approximation (elastic or isotropic scattering mechanisms) • Rode iterative method (scattering mechanisms are neither elastic nor isotropic) • High Electric Fields • Drift-Diffusion approaches • Hydrodynamic approaches • Monte Carlo Method for solving the BTE • Spherical Harmonics methods • Direct Poisson-Boltzmann solvers Covered in this course

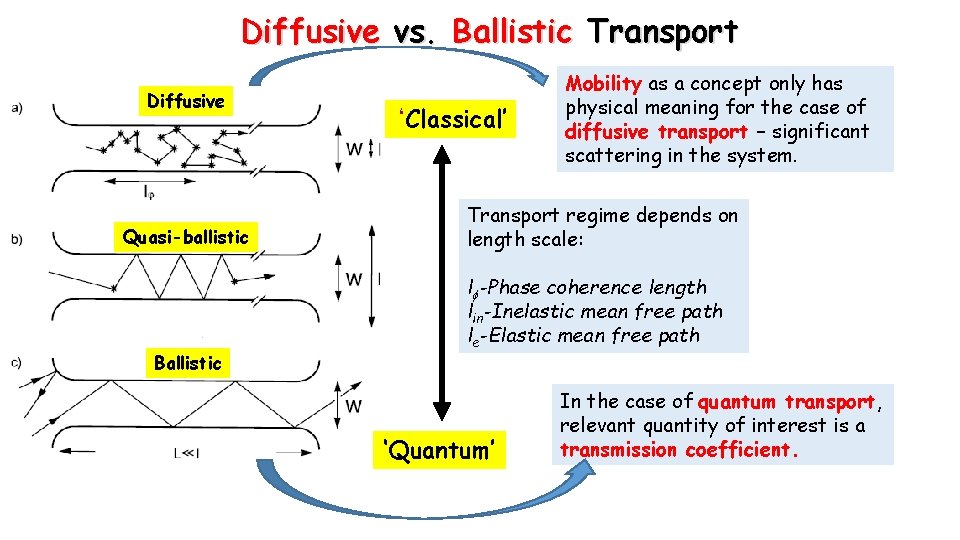
Diffusive vs. Ballistic Transport Diffusive Quasi-ballistic Ballistic ‘Classical’ Mobility as a concept only has physical meaning for the case of diffusive transport – significant scattering in the system. Transport regime depends on length scale: l -Phase coherence length lin-Inelastic mean free path le-Elastic mean free path ‘Quantum’ In the case of quantum transport, relevant quantity of interest is a transmission coefficient.

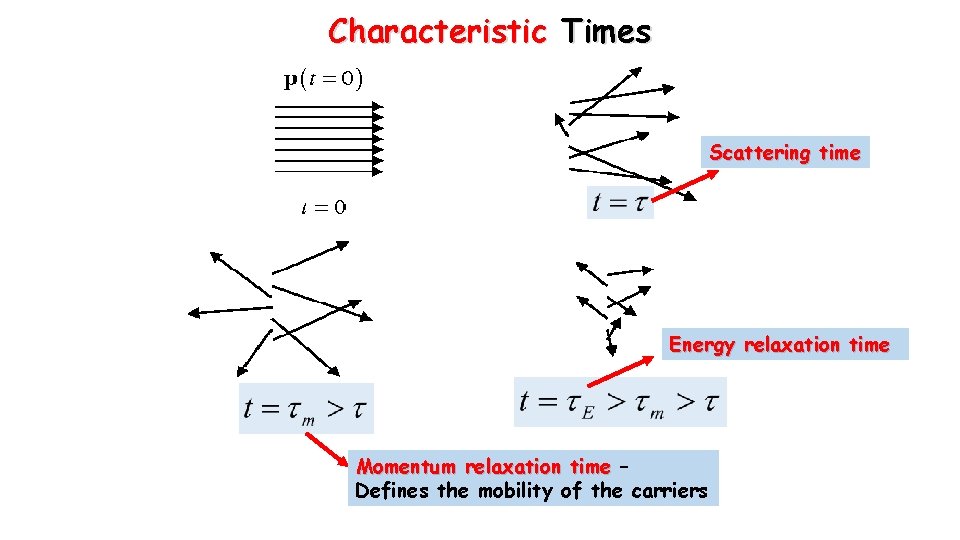
Characteristic Times Scattering time Energy relaxation time Momentum relaxation time – Defines the mobility of the carriers

III. Relaxation-Time Approximation (RTA) Most conventional device simulations are based on approximate models for transport which derived from the BTE, coupled to Poisson’s equation for self-consistency. In the simplest approach, the relaxation-time approximation is invoked, where the total distribution function is split into a symmetric term in terms of momentum (which is generally large) and an asymmetric term in the momentum (which is small):

RTA – Simplification of Collision Integral [1] For non-degenerate semiconductors, (1 -f) ≈ 1, the collision integral may be written: We now, consider two cases: (1) Equilibrium conditions when f. A=0 (2)Non-equilibrium conditions when f. A≠ 0

RTA – Simplification of Collision Integral [2] (2) Non-equilibrium conditions: (1) Equilibrium conditions: Case 2 Case 1

RTA – Plausible Form for the Distribution Function [3] a characteristic time that describes how the distribution function relaxes to its equilibrium form (independent of distribution function and applied electric field – Important restriction for the RTA to be valid) At low fields: At high fields:

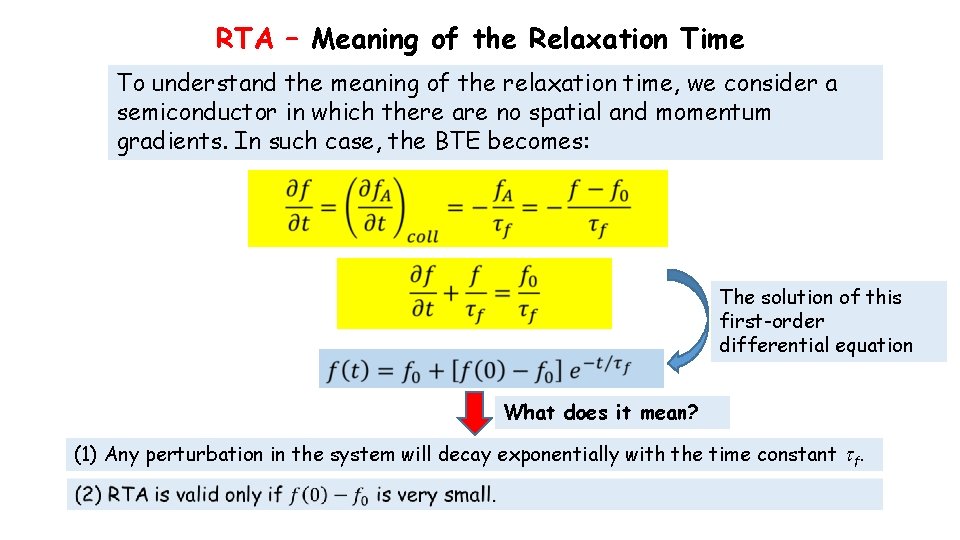
RTA – Meaning of the Relaxation Time To understand the meaning of the relaxation time, we consider a semiconductor in which there are no spatial and momentum gradients. In such case, the BTE becomes: The solution of this first-order differential equation What does it mean? (1) Any perturbation in the system will decay exponentially with the time constant tf.

IV. Solving BTE in the Relaxation-Time Approximation

Solving BTE in the RTA – Simplification [1] For parabolic bands and choosing the coordinate system such that the electric field is along z-axis, one can expand the distribution function into Legendre polynomials. For sufficiently low field, only the lowest order term is important, so that: the angle between the applied electric field (along the symmetry axis) and the momentum of carriers

Solving BTE in the RTA – Simplification [2] For parabolic bands and choosing the coordinate system such that the electric field is along z-axis, one can expand the distribution function into Legendre polynomials. For sufficiently low field, only the lowest order term is important, so that: the angle between the applied electric field (along the symmetry axis) and the momentum of carriers Substituting the results on the LHS of the BTE and using parabolic dispersion relation gives:

Solving BTE in the RTA – Collision Integral [3] We now consider the collision integral of the RHS of the BTE. Substituting the first order approximation for f(p) gives:

Solving BTE in the RTA – Choice of Coordinate System [4] To simplify the previous result, we consider the following coordinate system: Within this coordinate system, we have:

Solving BTE in the RTA – Collision Integral [5] The integration over j will make this term vanish, so we can write: To summarize: Next: Let’s consider two cases for the collision integral: (1) Elastic Scattering Process and (2) Isotropic Scattering Process

Solving BTE in the RTA – Elastic Scattering [6] Conclusion: When the scattering is elastic, the characteristic time tf equals the momentum relaxation time.

Solving BTE in the RTA – Isotropic Scattering [7] In the case of isotropic scattering process S(k, k’) does not depend upon a, so the second term in the square brackets averages to zero: Conclusion: When the scattering is isotropic, the characteristic time tf equals the scattering time or the average time between collision events.

Solving BTE in the RTA – Low-field Distribution Function [8] Summary: Under low-field conditions, when the scattering process is either elastic or isotropic, the collision term can be represented as – f. A/tf(k), where in general tf(k) is the momentum relaxation time that depends only of the nature of scattering process. 1 The BTE under this assumption 2 The distribution function is thus equal to: 3

Solving BTE in the RTA – Low-field Distribution Function [9] This term resembles the linear term in the Taylor series expansion of f(k). Conclusion: The displaced Maxwellian is a good representation of the distribution function under low-field conditions.