SP 225 Lecture 10 The Central Limit Theorem

  • Slides: 24
Download presentation
SP 225 Lecture 10 The Central Limit Theorem

SP 225 Lecture 10 The Central Limit Theorem

Differences Between Statistics and Parameters Sample: 3 Randomly Selected People Population: All People Parameter:

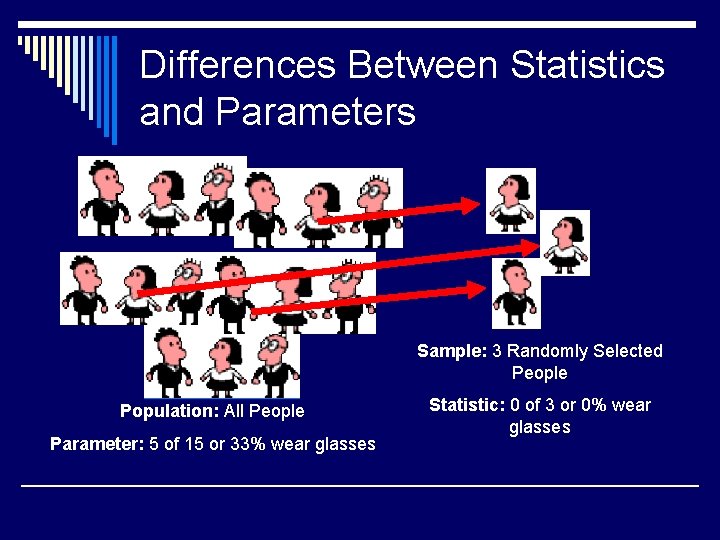
Differences Between Statistics and Parameters Sample: 3 Randomly Selected People Population: All People Parameter: 5 of 15 or 33% wear glasses Statistic: 0 of 3 or 0% wear glasses

Methods to for Better Samples o Random sampling makes samples representative o Book term:

Methods to for Better Samples o Random sampling makes samples representative o Book term: probability sample o EPSEM (Equal probability of selectino method)

EPSEM Technique o Begin with a list of all population members o Generate random

EPSEM Technique o Begin with a list of all population members o Generate random numbers to identify members of the list to be selected in the sample o Do everything possible to get selected members to participate in the survey

Sampling Distributions o The shape, measure of center and measure of variation associated with

Sampling Distributions o The shape, measure of center and measure of variation associated with many sample statistics o Unique and different from the population distribution

Three Separate Distributions o Sample distribution n Empirical and known n Intended to help

Three Separate Distributions o Sample distribution n Empirical and known n Intended to help learn about the population o Population distribution n Empirical and unknown n Properties estimated using statistics o Sampling distribution n Theoretical or non-empirical n Properties well-known and based on probabilities

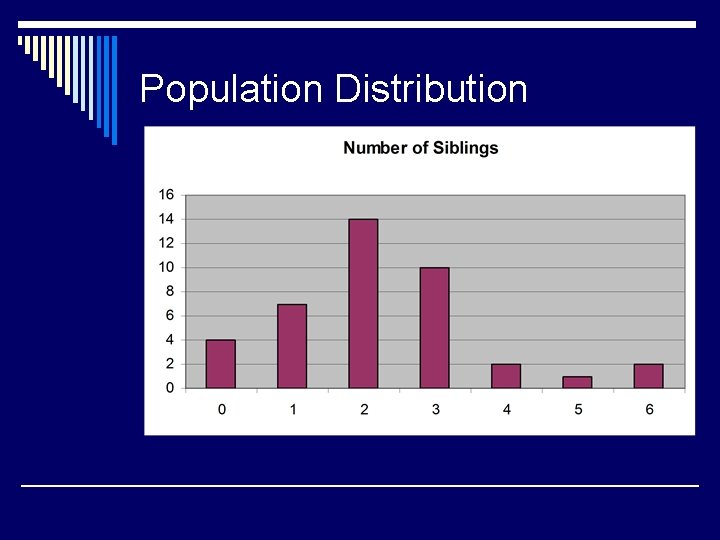
Population Distribution

Population Distribution

Population Distribution

Population Distribution

Sample Distribution

Sample Distribution

Sampling Distribution of Mean

Sampling Distribution of Mean

Central Limit Theorem o For normally distributed populations o If repeated samples of size

Central Limit Theorem o For normally distributed populations o If repeated samples of size N are drawn from a normal population with mean µ and standard deviation σ, then the sampling distribution σ of sample means will be normal with a mean of µ and a standard deviation of σ/√N

Central Limit Theorem o For any population o If repeated samples of size N

Central Limit Theorem o For any population o If repeated samples of size N are drawn from a normal population with mean µ and standard deviation , then, as N becomes large, the sampling distribution σ of sample means will be normal with a mean of µ and a standard deviation of σ/√N

The Probability Distribution o We can calculate probabilities for sample means using the sampling

The Probability Distribution o We can calculate probabilities for sample means using the sampling distribution for sample means o Similar to calculating probabilities for an individual using a population distribution o Use standard deviation of the sampling distribution instead of sampling distribution of the population

Empirical Rule for Data with a Bell -Shaped Distribution (3)

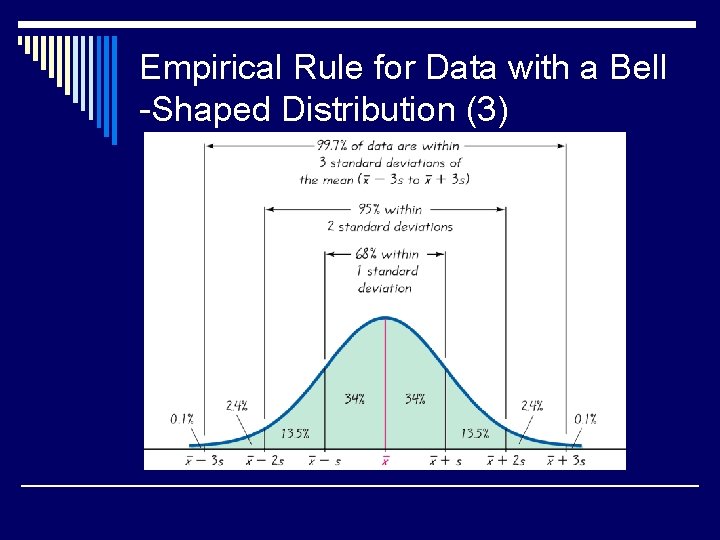
Empirical Rule for Data with a Bell -Shaped Distribution (3)

Example Problem (1) o The average GPA at a particular school is m=2. 89

Example Problem (1) o The average GPA at a particular school is m=2. 89 with a standard deviation s=0. 63. A random sample of 25 students is collected. Find the probability that the average GPA for this sample is greater than 3. 0.

Example Problem (2) The time it takes students in a cooking school to learn

Example Problem (2) The time it takes students in a cooking school to learn to prepare seafood gumbo is a random variable with a normal distribution where the average is 3. 2 hours with a standard deviation of 1. 8 hours. n Find the probability that the average time it will take a class of 36 students to learn to prepare seafood gumbo is less than 3. 4 hours. n Find the probability that it takes one student between 3 and 4 hours to learn to prepare seafood gumbo.

Confidence Interval o Mathematical statement that says that the parameter lies within a certain

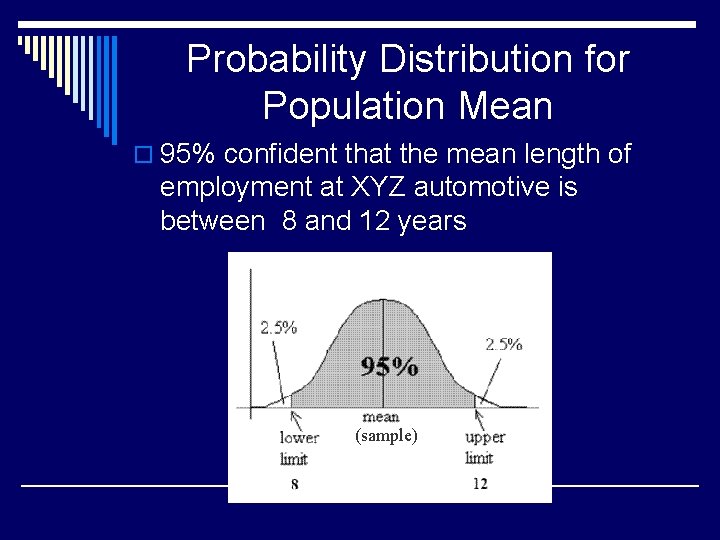
Confidence Interval o Mathematical statement that says that the parameter lies within a certain range of values o The average employee of XYZ Automotive has been employed between 8 and 12 years o 95% confident that the mean length of employment at XYZ automotive is between 8 and 12 years

Probability Distribution for Population Mean o 95% confident that the mean length of employment

Probability Distribution for Population Mean o 95% confident that the mean length of employment at XYZ automotive is between 8 and 12 years (sample)

Confidence Level o Percent of confidence intervals that contain the population mean over the

Confidence Level o Percent of confidence intervals that contain the population mean over the long run o Probability this confidence interval contains the population mean o 95% confident that the mean length of employment at XYZ automotive is between 8 and 12 years o 99% confident that the mean length of employment at XYZ automotive is between 8 and 12 years

Confidence Interval Formula

Confidence Interval Formula

Confidence Interval Estimate

Confidence Interval Estimate

Confidence Interval Example o A random sample of 100 television programs contained an average

Confidence Interval Example o A random sample of 100 television programs contained an average of 2. 37 acts of physical violence per program. The standard deviation of the number of acts of violence on television is 3. At the 99% level, what is your estimate of the mean number of acts of violence for all television programs?

Alpha o Percent of confidence intervals that DO NOT contain the population mean over

Alpha o Percent of confidence intervals that DO NOT contain the population mean over the long run o Probability this confidence interval DOES NOT contain the population mean o Complement of confidence level

Efficiency o Extent to which the confidence interval clusters around the mean o Width

Efficiency o Extent to which the confidence interval clusters around the mean o Width of the confidence interval o Determined by population standard deviation and sample size

Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The central limit theorem andCentral Limit Theorem The central limit theorem and
Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The theorem states that theCentral Limit Theorem The theorem states that the
LIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSILIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSI
Limit Sets Limit Sets Defined Limit Sets groupsLimit Sets Limit Sets Defined Limit Sets groups
LIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsiLIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsi
Limit MATHEMATICS LIMIT CRASH COURSE Limit of aLimit MATHEMATICS LIMIT CRASH COURSE Limit of a
limit Limit f limit f 0limit f xlimit Limit f limit f 0limit f x
Central Limit Theorem l Sampling Distributions l CentralCentral Limit Theorem l Sampling Distributions l Central
Ch 7 Central Limit Theorem Use the CentralCh 7 Central Limit Theorem Use the Central
The Central Limit Theorem for Proportions Lecture 26The Central Limit Theorem for Proportions Lecture 26
Lecture 5 slides on Central Limit Theorem StratifiedLecture 5 slides on Central Limit Theorem Stratified
SHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean TheoremSHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
VARIGNONS THEOREM What is Varigons Theorem The theoremVARIGNONS THEOREM What is Varigons Theorem The theorem
Thvenins Theorem Thevenins Theorem Thevenins theorem simplifies theThvenins Theorem Thevenins Theorem Thevenins theorem simplifies the
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is
Bayes Theorem Basics Total probability Theorem Bayes TheoremBayes Theorem Basics Total probability Theorem Bayes Theorem
BINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIALBINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIAL
CENTRAL LIMIT THEOREM p p p specifies aCENTRAL LIMIT THEOREM p p p specifies a
1162014 7 3 B The Central Limit Theorem1162014 7 3 B The Central Limit Theorem
Who is the Central Limit Theorem Michael SchneierWho is the Central Limit Theorem Michael Schneier