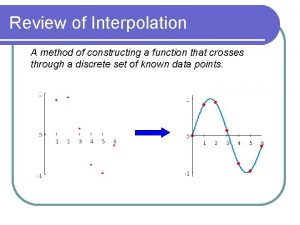
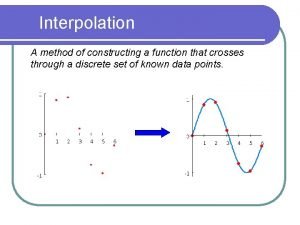
Review of Interpolation A method of constructing a

















- Slides: 25

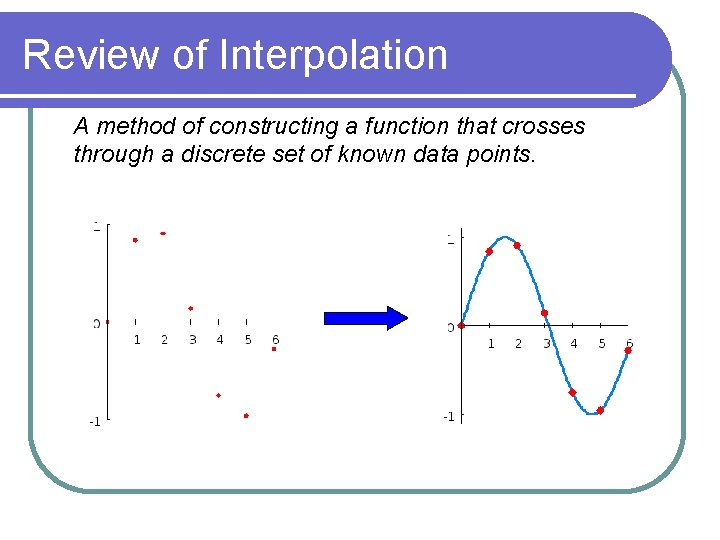
Review of Interpolation A method of constructing a function that crosses through a discrete set of known data points. .

Spline (general case) Given n+1 distinct knots xi such that: with n+1 knot values yi find a spline function with each Si(x) a polynomial of degree at most n.

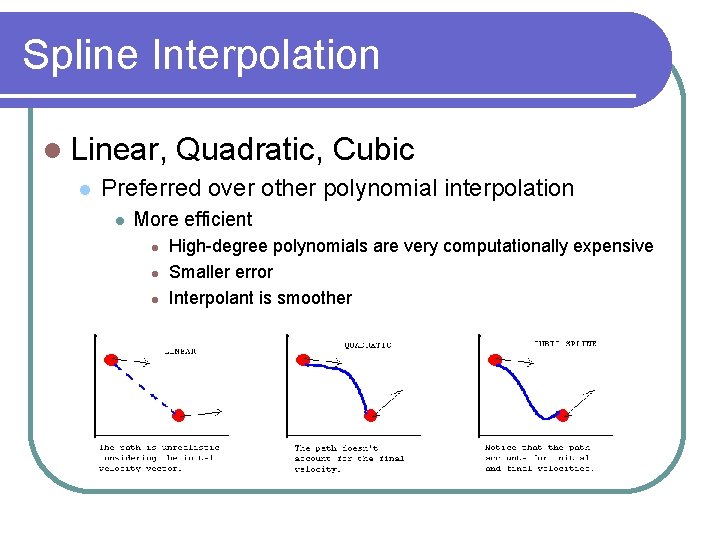
Spline Interpolation Linear, Quadratic, Cubic Preferred over other polynomial interpolation More efficient High-degree polynomials are very computationally expensive Smaller error Interpolant is smoother

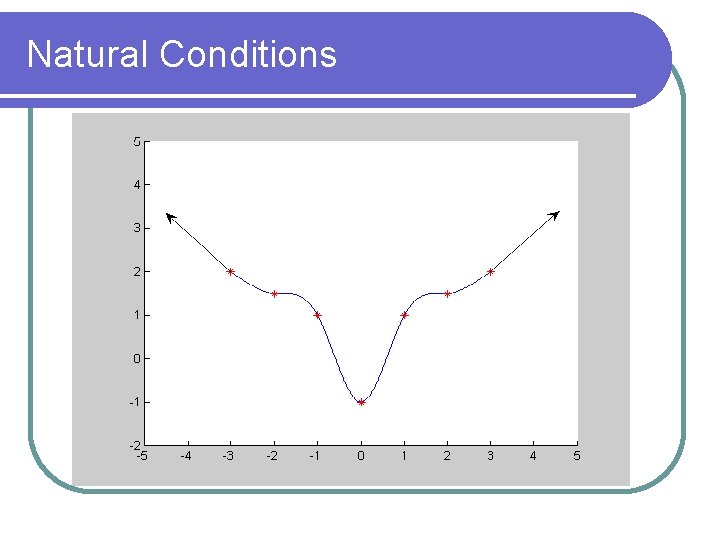
Natural Cubic Spline Interpolation Si(x) 4 Coefficients with n subintervals = 4 n equations There are 4 n-2 conditions = aix 3 + bix 2 + cix + di Interpolation conditions Continuity conditions Natural Conditions S’’(x 0) = 0 S’’(xn) = 0

Natural Conditions

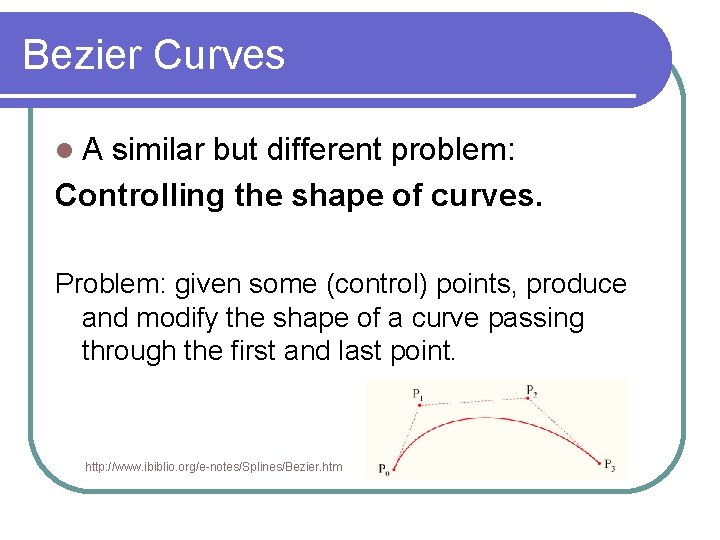
Bezier Curves A similar but different problem: Controlling the shape of curves. Problem: given some (control) points, produce and modify the shape of a curve passing through the first and last point. http: //www. ibiblio. org/e-notes/Splines/Bezier. htm

Bezier Curves Idea: Build functions that are combinations of some basic and simpler functions. Basic functions: B-splines Bernstein polynomials

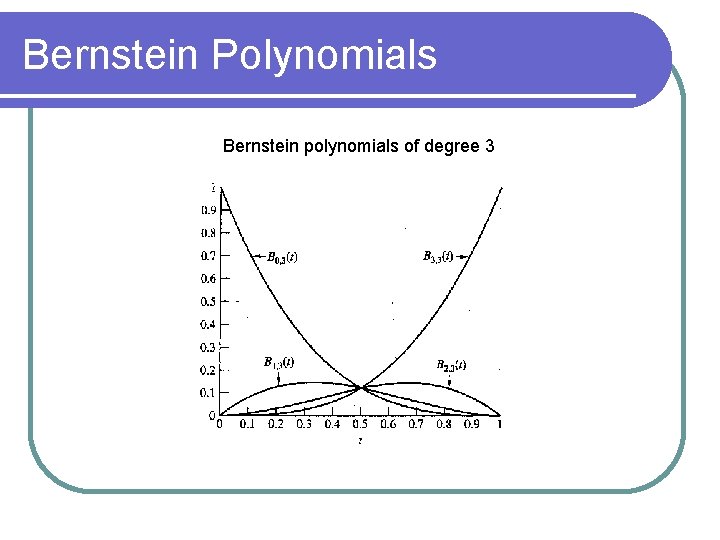
Bernstein Polynomials Bernstein polynomials of degree n are defined by: For v = 0, 1, 2, …, n, In general there are N+1 Bernstein Polynomials of degree N. For example, the Bernstein Polynomials of degrees 1, 2, and 3 are: 1. B 0, 1(t) = 1 -t, B 1, 1(t) = t; 2. B 0, 2(t) = (1 -t)2, B 1, 2(t) = 2 t(1 -t), B 2, 2(t) = t 2; 3. B 0, 3(t) = (1 -t)3, B 1, 3(t) = 3 t(1 -t)2, B 2, 3(t)=3 t 2(1 -t), B 3, 3(t) = t 3;

Deriving the Basis Polynomials Write 1 = t + (1 -t) and raise 1 to the third power for cubic splines (2 for quadratic, 4 for quartic, etc…) 1^3 = (t + (1 -t))^3 = t^3 + 3 t^2(1 -t) + 3 t(1 -t)^2 + (1 -t)^3 The basis functions are the four terms: B 0(t) = (1 -t)^3 B 1(t) = 3 t(1 -t)^2 B 2(t) = 3 t^2(1 -t) B 3(t) = t^3

Bernstein Polynomials Bernstein polynomials of degree 3

Using the Basis Functions To use the Bernstein basis functions to make a spline we need 4 “control” points for a cubic. (3 for quadratic, 5 for quartic, etc…) Let (x 0, y 0), (x 1, y 1), (x 2, y 2), (x 3, y 3) be the “control”points The x and y coordinates of the cubic Bezier spline are given by: x(t) = x 0 B 0(t) + x 1 B 1(t) +x 2 B 2(t) + x 3 B 3(t) y(t) = y 0 B 0(t) + y 1 B 1(t) + y 2 B 2(t) + y 3 B 3(t) Where 0<= t <= 1.

Bernstein Polynomials Given a set of control points {Pi}Ni=0, where Pi = (xi, yi). A Bezier curve of degree N is: P(t) = N i=0 Pi. Bi, N(t), Where Bi, N(t), for I = 0, 1, …, N, are the Bernstein polynomials of degree N. P(t) is the Bezier curve Since Pi = (xi, yi) x(t) = Ni=0 xi. Bi, N(t) and y(t) = Ni=0 yi. Bi, N(t) The spline goes through (x 0, y 0) and (x 3, y 3) The tangent at those points is the line connecting (x 0, y 0) to (x 1, y 1) and (x 3, y 3) to (x 2, y 2). The positions of (x 1, y 1) and (x 2, y 2) determine the shape of the curve.

Bernstein Polynomials Example Find the Bezier curve which has the control points (2, 2), (1, 1. 5), (3. 5, 0), (4, 1). Substituting the x- and y-coordinates of the control points and N=3 into the x(t) and y(t) formulas on the previous slide yields x(t) = 2 B 0, 3(t) + 1 B 1, 3(t) + 3. 5 B 2, 3(t) + 4 B 3, 3(t) y(t) = 2 B 0, 3(t) + 1. 5 B 1, 3(t) + 0 B 2, 3(t) + 1 B 3, 3(t)

Bernstein Polynomials Example Substitute the Bernstein polynomials of degree three into these formulas to get x(t) = 2(1 – t)3 + 3 t(1 – t)2 + 10. 5 t 2(1 – t) + 4 t 3 y(t) = 2(1 -t)3 + 4. 5 t(1 – t)2 + t 3 Simplify these formulas to yield the parametric equation: P(t) = (2 – 3 t + 10. 5 t 2 – 5. 5 t 3, 2 – 1. 5 t – 3 t 2 + 3. 5 t 3) where 0 < t < 1 P(t) is the Bezier curve http: //www. cs. brown. edu/exploratories/free. Software/repository/edu/brown/cs/exploratories/applets/bezier. Splines/bezier_splines_java_browser. html

Composite Bezier Curves In practice, shapes are often constructed of multiple Bezier curves combined together. Allows for flexibility in constructing shapes. (Consecutive Bezier curves need not join smoothly. )

Composite Bezier Curves Linking curves: Example: Find the composite Bezier curve for the four sets of control points: {(-9, 0), (-8, 1), (-8, 2. 5), (-4, 2. 5)}, {(-4, 2. 5), (-3, 3. 5), (-1, 4), (0, 4)} {(0, 4), (2, 4), (3, 4), (5, 2)}, {(5, 2), (6, 2), (20, 3), (18, 0)}

Composite Bezier Curves Use the same process as earlier to yield these four parametric equations: P 1(t) = (-9 + 3 t - 3 t 2 + 5 t 3, 3 t + 1. 5 t 2 - 2 t 3) P 2(t) = (-4 + 3 t 2 - 2 t 3, 2. 5 + 3 t - 1. 5 t 2) P 3(t) = (6 t - 3 t 2 + 2 t 3, 4 - 2 t 3) P 4(t) = (5 + 3 t + 39 t 2 - 29 t 3, 2 + 3 t 2 - 5 t 3)

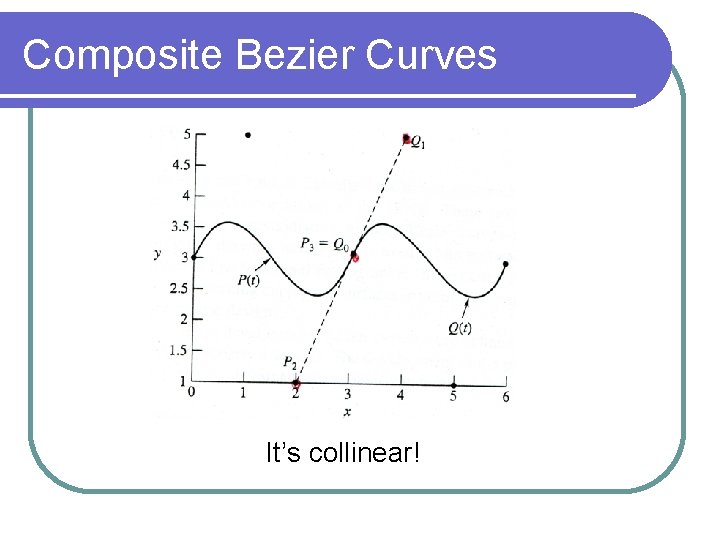
Composite Bezier Curves Linking Curves Smoothly To have two Bezier curves P(t) and Q(t) meet smoothly would require: PN = Q 0 P’(PN) = Q’(Q 0) It is sufficient to require that the control points PN-1, PN = Q 0, and Q 1 be collinear.

Composite Bezier Curves Example of collinear control points: {(0, 3), (1, 5), (2, 1), (3, 3)} and {(3, 3), (4, 5), (5, 1), (6, 3)} P(t) = (3 t, 3 + 6 t - 18 t 2 + 12 t 3) Q(t) = (3 + 3 t, 3 + 6 t – 18 t 2 + 12 t 3) and P’(t) = (3, 6 – 36 t + 36 t 2) Q’(t) = (3, 6 – 36 t + 36 t 2) Substituting t = 1 and t = 0 into P’(t) and Q’(t), yields P’(1) = (3, 6) = Q’(0)

Composite Bezier Curves It’s collinear!

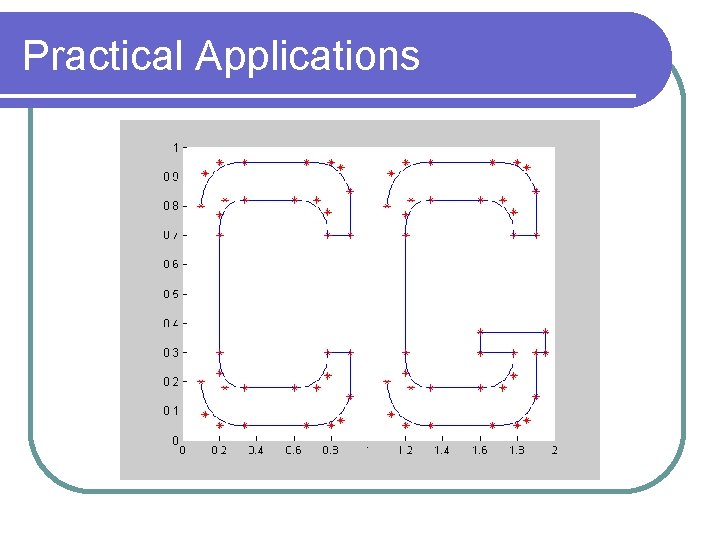
Practical Applications

Practical Applications • • • • • 0. 900 0. 850 0. 900 0. 700 0. 900 0. 850 0. 930 0. 800 0. 950 0. 666 0. 950 0. 333 0. 050 0. 666 0. 050 0. 100 0. 800 0. 120 0. 910 0. 200 0. 950 0. 333 0. 950 0. 100 0. 800 0. 100 0. 200 0. 120 0. 090 0. 200 0. 050 0. 333 0. 950 0. 666 0. 950 0. 900 0. 150 0. 850 0. 070 0. 800 0. 050 0. 666 0. 050 0. 900 0. 150 0. 900 0. 300 0. 900 0. 700 0. 780 0. 720 0. 820 0. 600 0. 820 0. 900 0. 300 0. 780 0. 220 0. 720 0. 180 0. 600 0. 180 0. 200 0. 700 0. 200 0. 300 0. 600 0. 820 0. 333 0. 820 0. 600 0. 180 0. 333 0. 180 0. 230 0. 180 0. 200 0. 230 0. 200 0. 333 0. 820 0. 230 0. 820 0. 200 0. 770 0. 200 0. 700 • • • • • • 1. 900 0. 850 1. 900 0. 700 1. 900 0. 850 1. 850 0. 930 1. 800 0. 950 1. 666 0. 950 1. 333 0. 050 1. 666 0. 050 1. 100 0. 800 1. 120 0. 910 1. 200 0. 950 1. 333 0. 950 1. 100 0. 800 1. 100 0. 200 1. 120 0. 090 1. 200 0. 050 1. 333 0. 950 1. 666 0. 950 1. 900 0. 150 1. 850 0. 070 1. 800 0. 050 1. 666 0. 050 1. 900 0. 150 1. 900 0. 300 1. 900 0. 700 1. 780 0. 780 1. 720 0. 820 1. 600 0. 820 1. 780 0. 300 1. 780 0. 220 1. 720 0. 180 1. 600 0. 180 1. 200 0. 700 1. 200 0. 300 1. 600 0. 820 1. 333 0. 820 1. 600 0. 180 1. 333 0. 180 1. 230 0. 180 1. 200 0. 230 1. 200 0. 300 1. 333 0. 820 1. 230 0. 820 1. 200 0. 770 1. 200 0. 700 1. 780 0. 300 1. 600 0. 370 1. 950 0. 300 1. 900 0. 300

Practical Applications

Practical Applications 4. 35 0. 00 4. 35 0. 19 3. 53 0. 23 3. 39 0. 36 3. 39 1. 09 3. 39 1. 08 3. 39 6. 20 3. 93 6. 20 5. 07 6. 20 5. 29 6. 02 5. 52 4. 92 5. 76 4. 92 5. 70 6. 62 0. 30 6. 62 0. 24 4. 92 0. 30 6. 62 0. 48 4. 92 0. 24 4. 92 2. 07 6. 20 0. 93 6. 20 0. 71 6. 02 0. 48 4. 92 2. 61 6. 20 2. 07 6. 20 2. 61 1. 09 2. 61 1. 08 2. 61 6. 20 1. 65 0. 19 2. 47 0. 23 2. 61 0. 36 2. 61 1. 09 1. 65 0. 00 1. 65 0. 19 1. 65 0. 00 4. 35 0. 00

Bézier surfaces in computer graphics
 Spline interpolation vs polynomial interpolation
Spline interpolation vs polynomial interpolation Types of isometric projection
Types of isometric projection Value number method for constructing dag
Value number method for constructing dag Graphical method shear moment diagrams
Graphical method shear moment diagrams Interpolation method example
Interpolation method example Interpolasi data
Interpolasi data Linear interpolation formula
Linear interpolation formula Direct method interpolation
Direct method interpolation Direct interpolation method
Direct interpolation method Interpolation quadratic
Interpolation quadratic Lagrange
Lagrange Parabolic interpolation example
Parabolic interpolation example Introduction of symposium
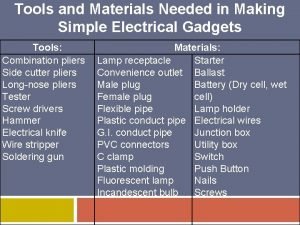
Introduction of symposium Materials and tools in making electrical gadgets
Materials and tools in making electrical gadgets Rules for constructing variable names in c
Rules for constructing variable names in c If ywz yxw what is true about xwz xwz is an obtuse angle
If ywz yxw what is true about xwz xwz is an obtuse angle Forming equations worksheet
Forming equations worksheet Constructing parallel lines
Constructing parallel lines Constructing perpendicular lines
Constructing perpendicular lines Constructing triangles worksheet
Constructing triangles worksheet Building pay structures
Building pay structures Architecture is the art and science of designing buildings
Architecture is the art and science of designing buildings What is square root spiral class 9
What is square root spiral class 9 Constructing bisectors
Constructing bisectors Interger constant
Interger constant How to construct a regular hexagon inscribed in a circle
How to construct a regular hexagon inscribed in a circle