DAY 37 CONSTRUCTING PERPENDICULAR LINES INTRODUCTION Two lines

DAY 37 – CONSTRUCTING PERPENDICULAR LINES

INTRODUCTION Two lines which intersect making a right angle are said to be perpendicular. In this lesson, we are going to learn various methods that we can use to construct lines intersecting at the right angle.

VOCABULARY Line segment This is a section of a line between two points. Perpendicular lines Are two lines which intersect making a right angle

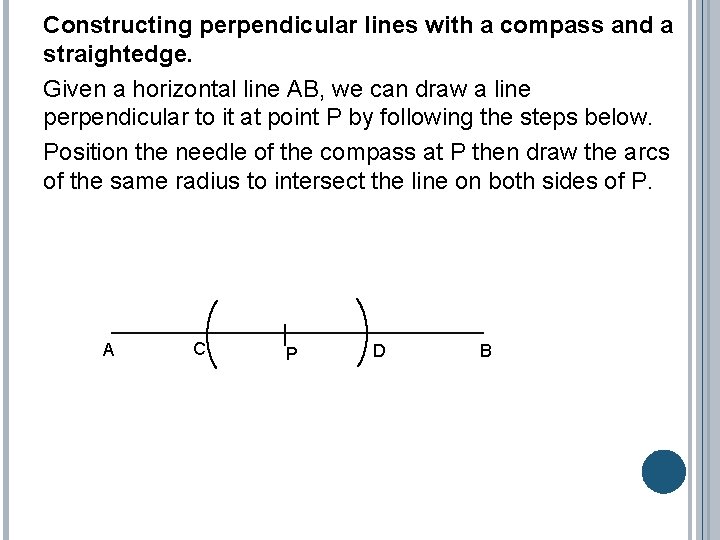
Constructing perpendicular lines with a compass and a straightedge. Given a horizontal line AB, we can draw a line perpendicular to it at point P by following the steps below. Position the needle of the compass at P then draw the arcs of the same radius to intersect the line on both sides of P. A C P D B

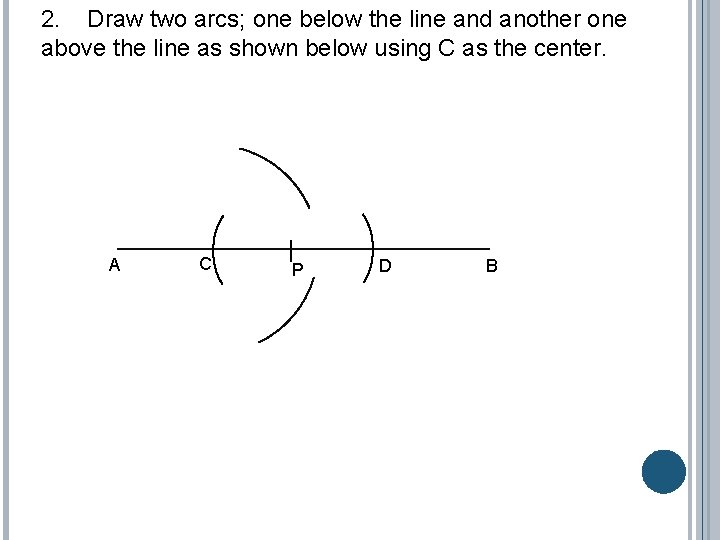
2. Draw two arcs; one below the line and another one above the line as shown below using C as the center. A C P D B

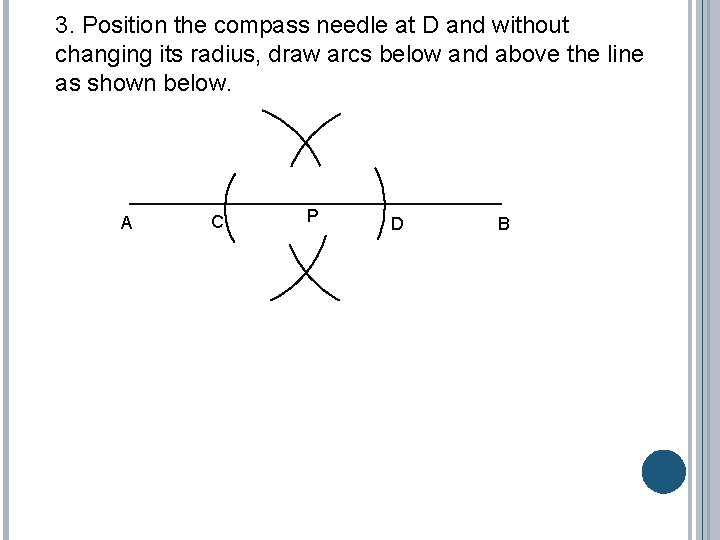
3. Position the compass needle at D and without changing its radius, draw arcs below and above the line as shown below. A C P D B

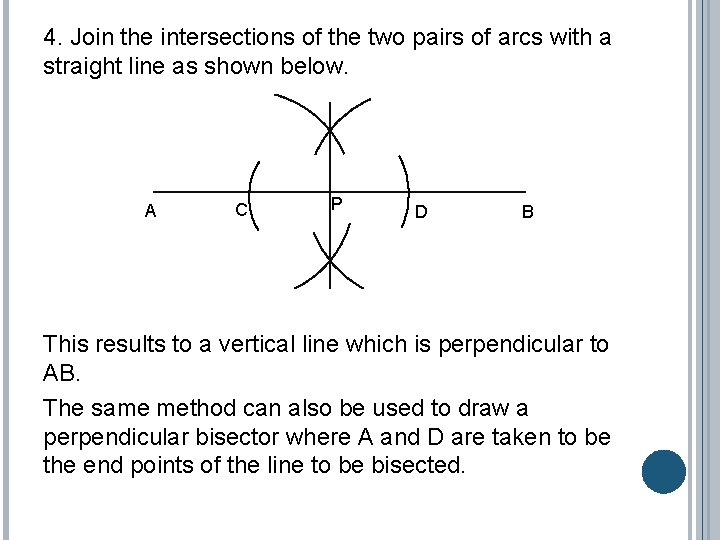
4. Join the intersections of the two pairs of arcs with a straight line as shown below. A C P D B This results to a vertical line which is perpendicular to AB. The same method can also be used to draw a perpendicular bisector where A and D are taken to be the end points of the line to be bisected.

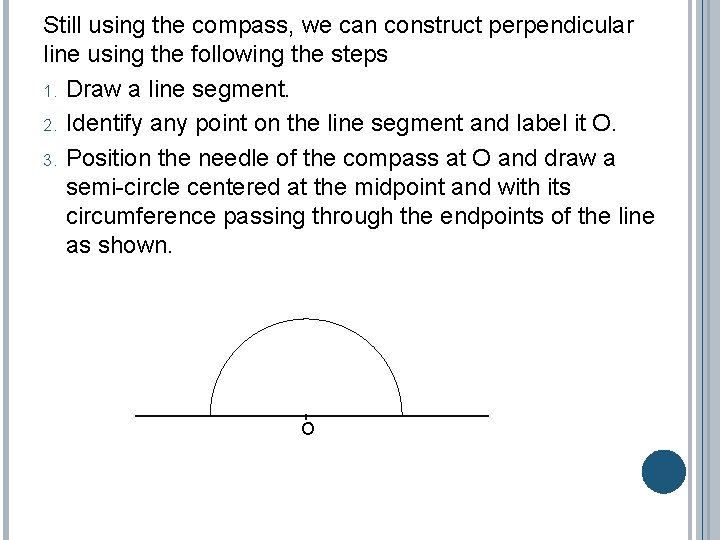
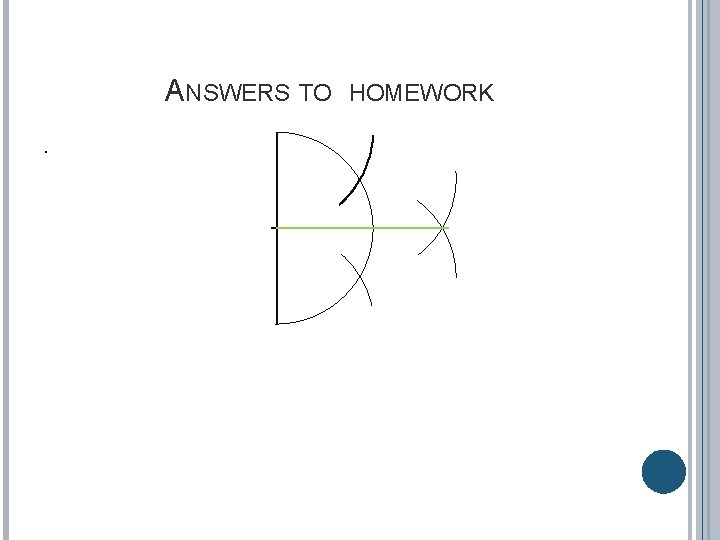
Still using the compass, we can construct perpendicular line using the following the steps 1. Draw a line segment. 2. Identify any point on the line segment and label it O. 3. Position the needle of the compass at O and draw a semi-circle centered at the midpoint and with its circumference passing through the endpoints of the line as shown. O

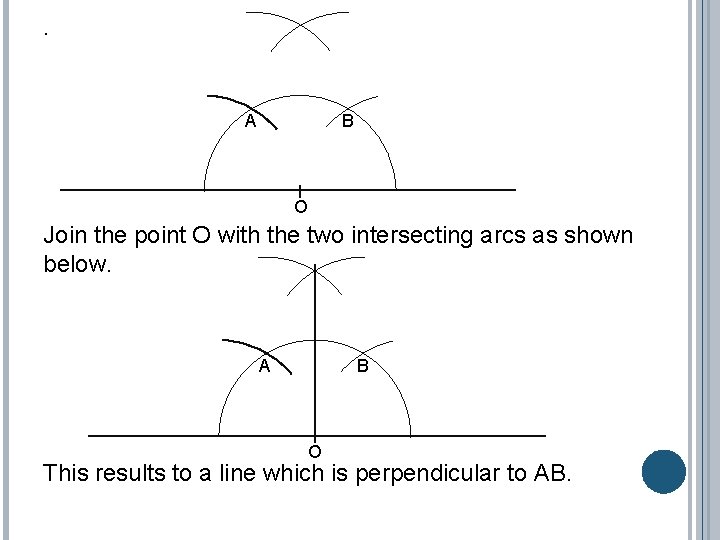
4. Without changing the radius of the compass, position the needle of the compass on one end and draw an arc that intersects the semi-circle. Label it as A. 5. Using the same compass radius, position the compass needle on the other end of the semicircle and draw an arc that intersects the semi-circle. Label it B. A B O 6. Using the same compass radius, position the compass needle at A and draw an arc above it. 7. Using the same compass radius, position the compass needle at B and draw an above B.

. A B O Join the point O with the two intersecting arcs as shown below. A B O This results to a line which is perpendicular to AB.

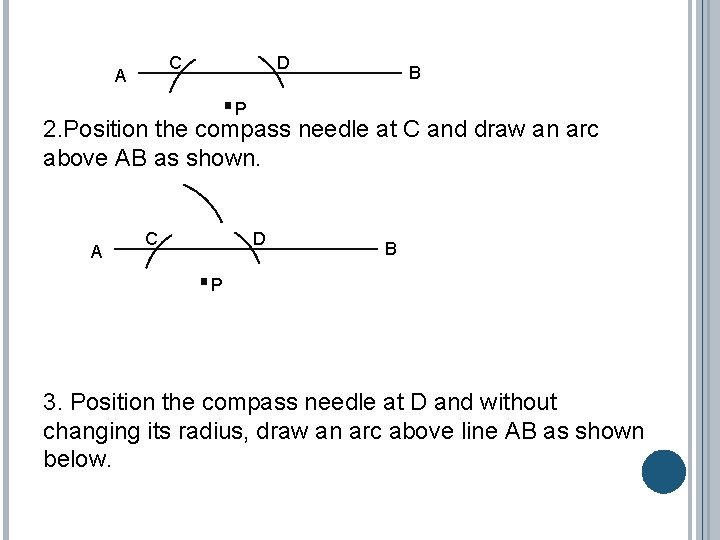
Constructing a perpendicular line through a given point. Sometimes we might be required to construct a perpendicular line to given line segment through a given point. For instance, we may be required to construct a line perpendicular to line AB through point P. B A P To this, we follow the steps below. 1. Position the needle of the compass at P then draw the arcs of the same radius to intersect the line on both sides of P. Label them C and D respectively.

C A D B P 2. Position the compass needle at C and draw an arc above AB as shown. A C D B P 3. Position the compass needle at D and without changing its radius, draw an arc above line AB as shown below.

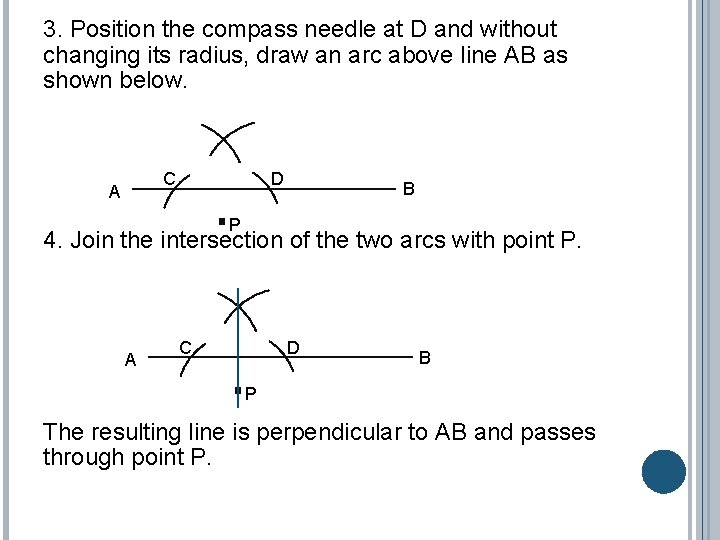
3. Position the compass needle at D and without changing its radius, draw an arc above line AB as shown below. C A D B P 4. Join the intersection of the two arcs with point P. A D C B P The resulting line is perpendicular to AB and passes through point P.

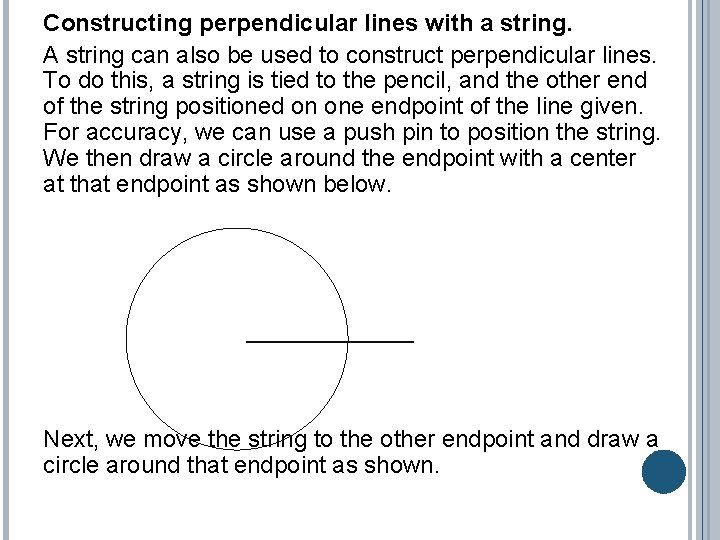
Constructing perpendicular lines with a string. A string can also be used to construct perpendicular lines. To do this, a string is tied to the pencil, and the other end of the string positioned on one endpoint of the line given. For accuracy, we can use a push pin to position the string. We then draw a circle around the endpoint with a center at that endpoint as shown below. 0 Next, we move the string to the other endpoint and draw a circle around that endpoint as shown.

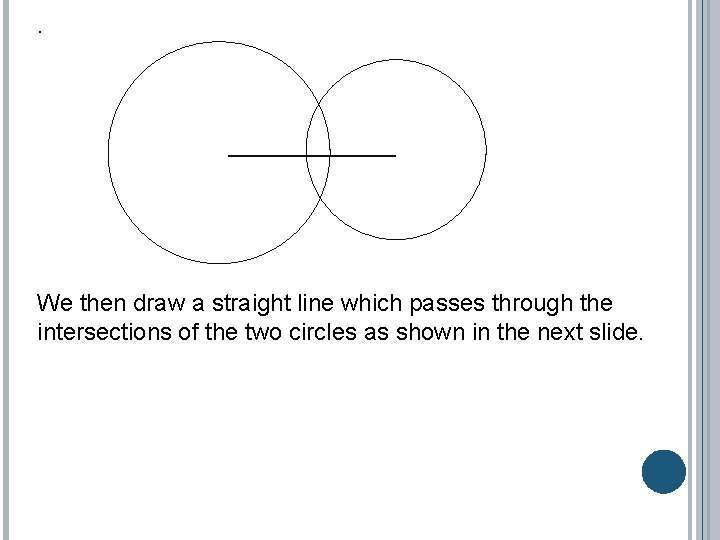
. 0 We then draw a straight line which passes through the intersections of the two circles as shown in the next slide.

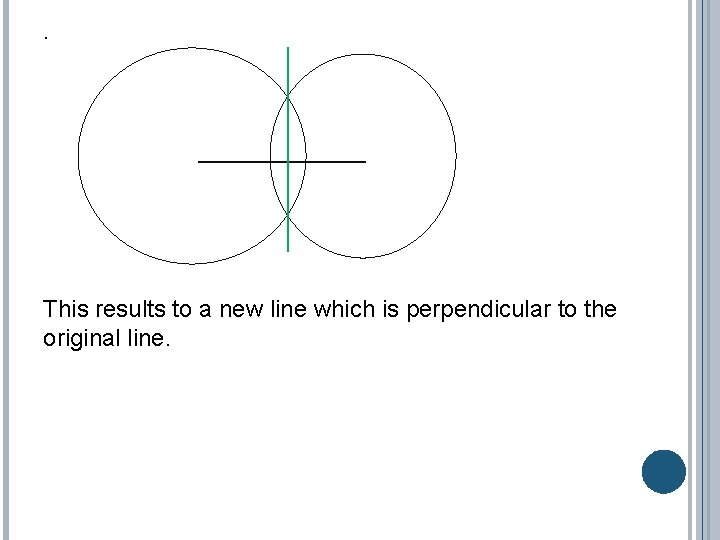
. 0 This results to a new line which is perpendicular to the original line.

Constructing perpendicular lines with a reflective device e. g. , plane mirror To do this, we follow the following steps. 1. Draw the line segment 2. Place the mirror vertically and crossing the line segment. 3. Adjust the mirror until the reflection of the line segment appears as a continuation of the line segment. 4. Hold the mirror in that position and then draw a straight line using the mirror as the straight edge. The resulting line is perpendicular to the line segment.

Constructing perpendicular lines by paper folding We first draw a line segment on a translucent paper then we fold the paper across the line segment such the endpoints of the line segment coincide. This folding creates a crease across the line segment. Draw a line along the crease created. This results in a perpendicular line passing through the midpoint of the original line segment.

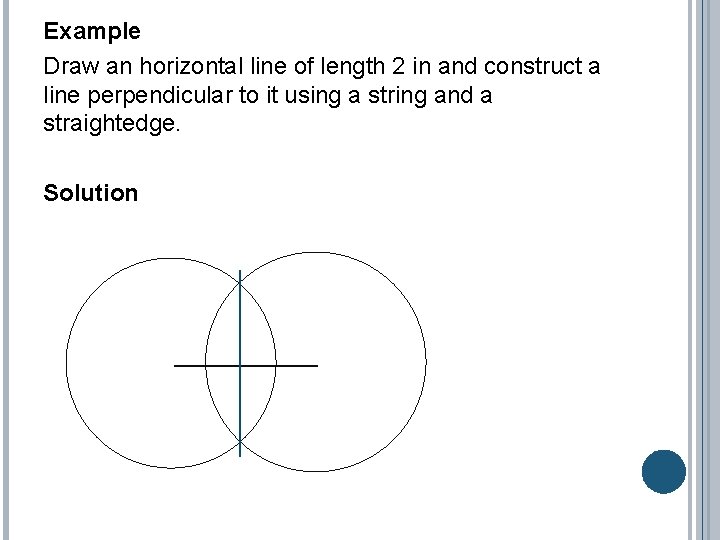
Example Draw an horizontal line of length 2 in and construct a line perpendicular to it using a string and a straightedge. Solution 0

HOMEWORK Using a compass and a straightedge construct a line which is perpendicular to the line given below.

ANSWERS TO. HOMEWORK

THE END