Interpolation Einleitung Geometrische Interpolation Polynominterpolation SplineInterpolation Inverse Distance

Interpolation • Einleitung • Geometrische Interpolation – Polynominterpolation – Spline-Interpolation – Inverse Distance Weighted Methode • Statistische Interpolation – Interpolation nach kleinsten Quadraten – Kovarianzfunktionen Ausgleichungsrechnung II Gerhard Navratil

Einleitung • Beschreibung flächenhafter Phänomene: Wert an jedem Punkt soll bestimmt sein • Geodäsie: Stützstellen gemessen • Zwischen Stützstellen: Schätzen der Werte = Interpolation • Außerhalb der Stützstellen: Extrapolation • Prädiktion: Interpolation oder Extrapolation Ausgleichungsrechnung II Gerhard Navratil

Beispiele • 2 x Höhenraster gemessen ohne Vermarkung – Vergleich der Epochen? • Mathematiker Abraham de Moivre: Prädiktion seines Todeszeitpunktes (Anwachsen des Schlafbedürfnisses) • Schriftsteller Mark Twain: Mississippi hat innerhalb von 176 Jahren Länge verkürzt vor 1 Mio Jahre 2 Mio km lang, in 650 Jahren 3 km lang Ausgleichungsrechnung II Gerhard Navratil

Problem der Interpolation • Messwerte an bekannten Punkten gegeben: Stützwerte an Stützstellen • Dimension der Stützstellen beliebig • Stützwerte und Stützstellen ergeben mathematische Funktion vom Grad 1+Dimension der Stützstellen • Dimension des Modells kleiner als der Dimension des Punkthaufens Ausgleichungsrechnung II Gerhard Navratil

Mathematische Beschreibung • Gesucht: Kontinuierlicher Verlauf einer diskret gegebenen Funktion • Häufig folgende Bedingungen – Räumlich nahe beieinander liegende Werte haben eine größere Ähnlichkeit als weit voneinander entfernte – An Stützstellen Interpolationswert = Stützwert (wenn nicht eingehalten: Approximation – z. B. kleinste Quadrate) Ausgleichungsrechnung II Gerhard Navratil

Unterscheidung • Geometrische Verfahren oder Interpolationsverfahren im engeren Sinn • Statistische Verfahren oder Prädiktionsverfahren Ausgleichungsrechnung II Gerhard Navratil

Geometrische Interpolation Ausgangslage: Funktion f(x) gegeben durch • n+1 diskrete Stützstellen x 0 < x 1 < … < xn • Stützwerte y 0 < y 1 < … < yn • Gesucht: Wert der Funktion an einer beliebigen Stelle x mit x 0 < xn Ausgleichungsrechnung II Gerhard Navratil

Polynominterpolation • Annahme eines Polynoms n-ten Grades • Zur Lösung unterschiedlichste Algorithmen in der Literatur • Problem: Starkes Ausschwingen • Reduktion: Nicht alle Stützstellen verwendet – Extremfall lineare Interpolation Ausgleichungsrechnung II Gerhard Navratil

Spline-Interpolation (1) • Gesucht: Glatte Kurve durch alle Stützstellen, möglichst stetig • Lösung: Dünne Latten (Straklatten) aus dem Schiffsbau – Latte minimiert die Biegeenergie • Vereinfachte physikalische Annahmen: Ausgleichungsrechnung II Gerhard Navratil

Spline-Interpolation (2) s(x) ist Variationsaufgabe unter folgenden Nebenbedingungen • s(x) muss Interpolationseigenschaft s(xi)=yi erfüllen • s(x) soll an inneren Stützstellen mindestens einmal stetig differenzierbar sein • Zwischen den Stützstellen mindestens 4 x stetig differenzierbar • s(x) soll minimieren Ausgleichungsrechnung II Gerhard Navratil

Spline-Interpolation (3) Lösung nach klassischer Variationsrechnung Ergebnis hat folgende Eigenschaften: • s(x) ist in jedem Teilintervall ein kubisches Polynom • 1. und 2. Ableitung von s(x) an inneren Stützstellen stetig • 2. Ableitung von s(x) verschwindet bei x 0, xn (natürliche Bedingung natürliche kubische Spline-Funktion) Ausgleichungsrechnung II Gerhard Navratil

Spline-Interpolation (4) Verallgemeinerung: Erhöhung der Ableitungen unter den Variationsintegral samt Anpassung der Nebenbedingungen Lösung der Variationsaufgabe • s(x) muss Interpolationseigenschaft s(xi)=yi erfüllen • s(x) soll an inneren Stützstellen mindestens (p-1) mal stetig differenzierbar sein • Zwischen den Stützstellen mindestens 2 p mal stetig differenzierbar • s(x) soll minimieren Ausgleichungsrechnung II Gerhard Navratil

Ausgleichungsrechnung II Gerhard Navratil

Berechnung kubische Spline (1) • Kubisches Polynom als Lösung für Intervall • Für Werte an Intervallenden: Ausgleichungsrechnung II Gerhard Navratil

Berechnung kubische Spline (2) Umschreiben der Gleichungen ergibt: Ausgleichungsrechnung II Gerhard Navratil

Berechnung kubische Spline (3) • Polynome berechenbar, wenn neben Stützwerten auch die 2. Ableitungen bekannt • Festgelegt sind nun – Interpolationseigenschaft – Stetigkeit der Funktion • Es fehlt: Stetigkeit an inneren Stützstellen Ausgleichungsrechnung II Gerhard Navratil

Berechnung kubische Spline (4) • Für erste Ableitung am Ende des Intervalls ergibt sich • Nach Substitution von i durch i-1 erhalten wir • Bedingung führt zu • oder Ausgleichungsrechnung II Gerhard Navratil

Berechnung kubische Spline (5) • Bedingung muss an allen inneren Stützstellen (1 … n-1) erfüllt sein • Also: n-1 lineare Gleichungen für n-1 Unbekannte (2. Ableitungen) Ausgleichungsrechnung II Gerhard Navratil

Beispiel mit n=5 (1) • Oder Ay´´- l=0 • Bei natürlicher Spline: y 0´´= y 5´´=0 Ausgleichungsrechnung II Gerhard Navratil

Beispiel mit n=5 (2) • Unter Annahme von äquidistanten Stützstellen vereinfacht sich das System zu Ausgleichungsrechnung II Gerhard Navratil

Rechenweg • Bestimmen der Intervalllängen • Gleichungssystem für 2. Ableitungen aufstellen • Auflösen 2. Ableitungen • Parameter der kubischen Polynome bestimmen Ausgleichungsrechnung II Gerhard Navratil

Allgemeine kubische Spline • Natürliche Randbedingungen durch andere Bedingungen ersetzt – 2. Ableitungen an Endpunkten ≠ 0 (s. o. ) – 2. Ableitung an Endpunkten Vielfaches der 2. Ableitung der benachbarten Stützpunkte – Vorgabe der 1. Ableitung • Leicht geänderte Systeme Ausgleichungsrechnung II Gerhard Navratil

Periodische Kubische Spline (1) • Interpolierende setzt sich außerhalb des Intervalls periodisch fort mit Periode T • Somit • Es muss für glatten Kurvenverlauf gelten Ausgleichungsrechnung II Gerhard Navratil

Periodische Kubische Spline (2) • Somit Ausgleichungsrechnung II Gerhard Navratil

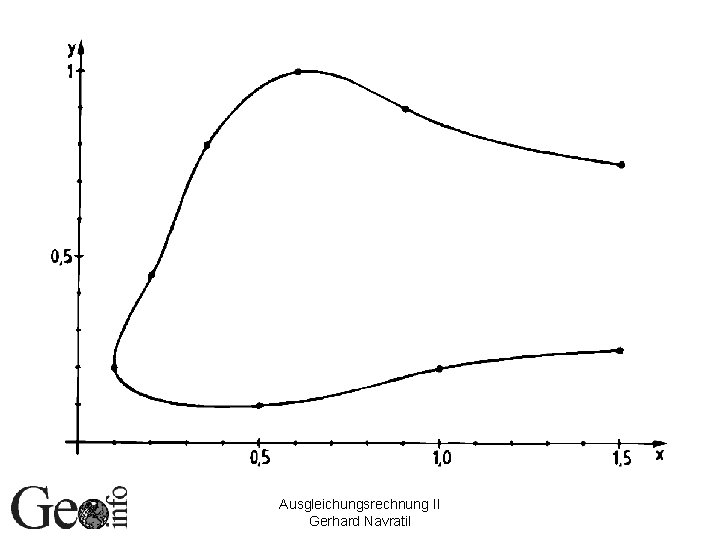
Glatte 2 D-Kurvendarstellung (1) • Gegeben (n+1) Punkte in der Ebene • Gesucht: möglichst glatte Kurve durch die Punkte • Lösung: Kurve in Parameterdarstellung • Parameter t: Kurvenlänge Ausgleichungsrechnung II Gerhard Navratil

Glatte 2 D-Kurvendarstellung (2) • Parameterwerte t 0, …, tn entsprechen den Punkten: zunehmende Wertefolge • Funktionen (tk, xk) und (tk, yk) – zugehörige Splines werden bestimmt mit k = 0 … n • Optimaler Parameter: Kurvenlänge – ist aber am Anfang nicht bekannt Distanzen aufeinander folgender Punkte Ausgleichungsrechnung II Gerhard Navratil

Ausgleichungsrechnung II Gerhard Navratil

Inverse Distance Weighted (1) • Spline: Rein mathematische Interpolation • Nun: Räumliches Problem • Ausgangspunkt: An verschiedenen Stellen Beobachtungen • Wir wollen: Aussagen über den Verlauf des Phänomens über die gesamte Fläche • z. B. Inverse Distance Weighted oder Shepard-Methode Ausgleichungsrechnung II Gerhard Navratil

Inverse Distance Weighted (2) • Schätzung eines Messwertes • di: Abstand Interpolationspunkt – Stützpunkt, also Gewicht umgekehrt proportional zu Distanz • Anzahl berücksichtigter Stützwerte ist individuell festzulegen (abhängig vom Abstand) Ausgleichungsrechnung II Gerhard Navratil

Statistische Interpolationsverfahren • Stützwerte in der Regeln physikalische Größen: Signale • Prädiktion: Beschreibung des Signalverlaufes aus einigen Signalen • Statistische Verfahren: Losgelöst von geometrischen Vorstellungen (rein stochastisch) • Kovarianzfunktion zwischen Signalen ist entscheidend • Weitere Annahme: Feld homogen und isotrop Ausgleichungsrechnung II Gerhard Navratil

Interpolation nach kleinsten Quadraten (1) • Gegeben: Korrelierte Beobachtungen l an Positionen x, Kovarianzmatrix C • Gesucht: Lokaler Wert lp and Position xp • Annahme: Wert über Linearkombination bestimmbar, also lp=a. Tl • Koeffizienten a noch zu bestimmen • Einführung eines fiktiven Messwertes gibt Ausgleichungsrechnung II Gerhard Navratil

Interpolation nach kleinsten Quadraten (2) • Für fiktiven Wert Varianz Cpp und Kovarianz clp führt zu • Fehlerfortpflanzungsgesetz liefert • Nach Moritz: Koeffizienten so bestimmen, dass Varianz von d ein Minimum wird, also Ausgleichungsrechnung II Gerhard Navratil

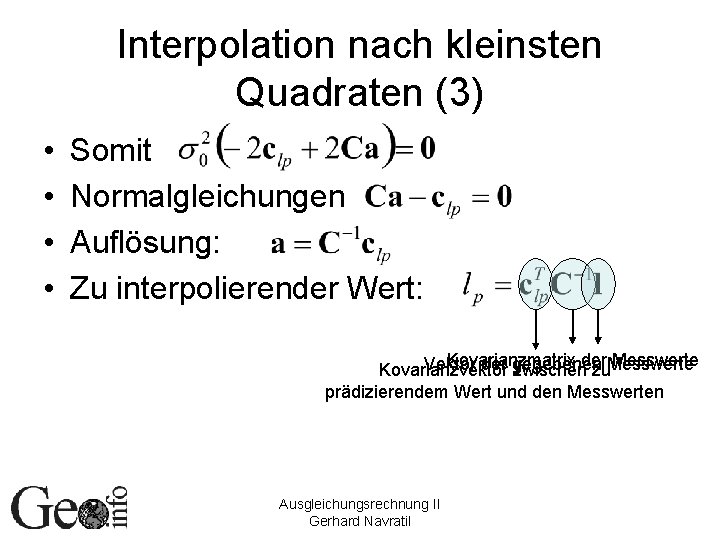
Interpolation nach kleinsten Quadraten (3) • • Somit Normalgleichungen Auflösung: Zu interpolierender Wert: Kovarianzmatrix der Messwerte Vektor der gegebenen Kovarianzvektor zwischen zu. Messwerte prädizierendem Wert und den Messwerten Ausgleichungsrechnung II Gerhard Navratil

Interpolation nach kleinsten Quadraten (4) • Elemente der Kovarianzmatrizen mit Hilfe eine Kovarianzfunktion C(s) bestimmt • C(s) basiert meist auf Abstand der Punkte, nicht auf Lage oder Richtung (homogen, isotrop) • Gleichzeitige Prädiktion mehrerer Werte führt zu Ausgleichungsrechnung II Gerhard Navratil

Interpolation nach kleinsten Quadraten (5) • Prädiktionsvarianz erhält man aus • Geodätische Anwendungen – Interpolation von Schwereanomalien – Interpolation/Transformation in Photogrammetrie und Landesvermessung Ausgleichungsrechnung II Gerhard Navratil

Kovarianzfunktionen (1) • Notwendig für Prädiktion nach kleinsten Quadraten • Beschreiben die Struktur des Feldes • Können aus umfangreichem Datenmaterial ermittelt werden (Varianz aller Daten, Kovarianzen bis zu bestimmtem Abstand, dann Funktion durchlegen) Ausgleichungsrechnung II Gerhard Navratil

Kovarianzfunktionen (2) Im allgemeinen sind folgende Eigenschaften gegeben: • Maximum im Nullpunkt • Zunehmender Abstand abnehmender Wert • Geht gegen 0 für s ∞ Ausgleichungsrechnung II Gerhard Navratil

Kovarianzfunktionen (3) • Manchmal auch mathematische Funktion direkt angegeben (wenn darauf geschlossen werden kann) • Häufig verwendet – Gauß‘sche Glockenkurve – Modell von Hirvonen Ausgleichungsrechnung II Gerhard Navratil