Revenue Optimization in Multi Dimensional Settings Constantinos Daskalakis

Revenue Optimization in Multi. Dimensional Settings Constantinos Daskalakis EECS, MIT Reference: http: //arxiv. org/abs/1207. 5518

► ► Revenue-optimization, so far Jason’s talk: § Bayesian mechanism design: Auction design in presence of stochastic information about the bidders. § Analysis tools: Bayes-Nash equilibrium. § Single-dimensional setting: 1 type of item, many bidders, constraints on who can be given an item simultaneously. § [Myerson’ 81]: Revenue-optimal auction in all single-dimensional settings. ► In fact, a reduction from auction- design to algorithm- design: Revenue optimization reduces to (virtual) welfare optimization. Tim’s talk: § Single-dimensional settings are not only optimally solvable, but also amenable to simple approximations. § “Exist constant-factor approximations which use little information about the bidders. ”

Beyond Single-Dimensional Settings online marketplaces - heterogeneous items - complicated allocation constraints sponsored search online inventory allocation spectrum auctions

Multi-dimensional Auction Setting 1 1 … … j i … … m n - Bidders have values on items and bundles of items. - Bidder’s valuation (or type) encodes that information. revenue/social welfare/other objective

Example Valuations - Example 1: Additive bidder - described by vector of values - their valuation is: (one value per item) - Example 2: Single-minded combinatorial bidder - described by the subset of items they desire S, and their value v - their valuation is: è For simplicity, throughout talk assume bidders are additive.

Multi-dimensional Auction Setting 1 … … j i - … … m revenue/social welfare/other objective 1 n universe of possible valuations for bidder i Bidders have values on items and bundles of items. Bidder’s valuation (or type) encodes that information. additive bidder: Bidders’ types (t 1, …, tm) come from known product distribution .

Multi-dimensional Auction Setting 1 … … j i - … … m revenue/social welfare/other objective 1 n universe of possible valuations for bidder i Bidders have values on items and bundles of items. Bidder’s valuation (or type) encodes that information. additive bidder: Bidders’ types (t 1, …, tm) come from known product distribution - Auctioneer will decide some allocation A [m] x [n], and charge prices. - There are (possibly combinatorial) constraints on what allocations are allowed. .

Example 1: selling paintings 1 1 … … j i … … m n - Items are paintings. - No painting should be given to more than one bidder - so:

Example 2: selling houses 1 1 … … j i - … … m n Items are houses. No house should be given to more than one bidder. No bidder should receive more than one house. so:

Example 3: selling doctor appointments 1 1 … … i j … … m n - Items are slots with doctors in a hospital. - No slot should be given to more than one bidder. - No bidder should get more than one slot with same doctor, or overlapping slots with different doctors.

Example 4: building bridges 1 … i … m - Items are possible locations for building a bridge L = {l 1, l 2, …, ln}. - If a location is given to one bidder, it is given to all bidders (as every bidder will use a bridge if it is built). - so:

Multi-dimensional Auction Setting revenue/social welfare/other objective 1 1 … … j i … … m n universe of possible valuations for bidder i - Bidders have values on items and bundles of items. - Bidder’s valuation (or type) encodes that information. - Bidders’ types (t 1, …, tm) come from known product distribution . - Auctioneer will decide some allocation A [m] x [n], and charge prices. - There are (possibly combinatorial) constraints on what allocations are allowed. - INPUT: m, n, T 1, …, Tm , , and some access to .

Auction in Action 1 1 expected welfare: … … i expected revenue: - chosen j by auction - Commits to an auction design, specifying allowed over bidders’ types t 1(i) , …, tm, the bidder actions, (ii)the allocation price rule; randomness in the auction, and (iii)the bidders’ - in Asks bidders play the auction; strategies Bayes Nashtoequilibrium - Implements the allocation and price n rule specified by the auction; - Goal: Optimize revenue/welfare. payment made by bidder i to the auctioneer Uses as input: the auction specification, her own type, and her beliefs about over bidders’ types t 1, …, tm, the types of the other bidders; randomness in the auction, and the bidders’ Chooses how to play; strategies in Bayesbundle Nash equilibrium Goal: optimize her own utility (= value for allocated – price charged). Each Bidder: - … … m outcome in Auctioneer:

background welfare vs revenue optimization in multidimensional settings

Welfare-Optimization ► [Vickrey-Clarke-Groves]: Mechanism design for welfare-optimization is no harder than algorithm design for welfare-optimization. ► the VCG auction (as a reduction): § bidders are asked to report their types: t 1, t 2, …, tm ; § the mechanism chooses the allocation ► obtained ; via a call to a welfare optimization algorithm § bidders are charged so that: reported types = true types. ► truthfulness-inducing payments can be computed via calls to a welfare optimization algorithm (e. g. Clarke pivot payments) Corollary: the only bottleneck to tractable welfare-optimizing mechanisms is whethere is a computationally efficient algorithm for the underlying welfare optimization problem. ► Approximation preserving mechanism-to-algorithm reduction ? ► § yes! [Hartline-Lucier’ 10, Hartline-Kleinberg-Malekian’ 11, Bei-Huang’ 11] § Spoiler Alert: Nicole will present these results.

Revenue-Optimization ► [Myerson ’ 81]: In all single-dimensional (i. e. single-item / single-item multi-unit) settings, mechanism design for revenue optimization reduces to algorithm design for welfare optimization. ► Myerson’s auction (as a reduction): § bidders are asked to report their types ; § reported types are transformed to virtual-types ; § the virtual-welfare maximizing allocation is chosen; ► this is a call to a welfare optimization algorithm § and prices are charged to make sure bidders report truthfully. ► truthfulness-inducing payments can be computed via calls to a welfare optimization algorithm Corollary: If the underlying welfare-maximization problem is tractable, then so is the revenue-optimal auction. ► Unanswered: Beyond single-item settings? Robustness to approximation; ► ► Myerson’s proof is “mystical; ” result comes mysteriously out of algebra…

Multi-Dimensional Auction Phenomena optimal mechanism: sell item for 1/2 expected revenue: 1/4 optimal mechanism ? idea 1: run n different auctions as above … … additive expected revenue: n/4 idea 2: offer the grand bundle of all the items at price expected revenue: moral of the story: bundling helps

Multi-Dimensional Auction Phenomena (2) [Thanassoulis’ 04]: - optimal deterministic mechanism: post price of $5. 097 on each item expected revenue: $5. 05 unit demand - a better randomized mechanism additionally sell for $5. 057 the lottery (1/2, 1/2) expected revenue: $5. 06 moral of the story: randomization helps [Briest-Chawla-Kleinberg-Weinberg’ 10]: gap may be arbitrarily high in general [Chawla-Malec-Sivan’ 10]: for independent values, unit-demand bidders, gap is at most a factor of 34.

Multi-dimensional Mechanisms (known results prior to FOCS’ 12) ► Large body of work in Economics: multi- to single§ [Mc. Afee-Mc. Millan’ 88], [Wilson’ 93], [Armstrong’ 96], [Rochet-Chone’ 98], dimensional reduction [Armstrong’ 99], [Zheng’ 00], [Basov’ 01], [Kazumori’ 01], [Thanassoulis’ 04], [Vincent-Manelli’ 06], [Vincent-Manelli’ 07], … § Progress sporadic. ► Recently (2007 -today), algorithmic tools enabled progress. § constant-factor approximations (limited settings) ► [Chawla-Hartline-Kleinberg ’ 07], [Chawla et al’ 10], [Bhattacharya et al’ 10], [Alaei’ 11], [Hart-Nisan ’ 12], [Kleinberg-Weinberg ’ 12], [Alaei et al’ 12] § exact solutions (limited settings) ► [Cai-D ’ 11], [D-Weinberg ’ 12], [Cai-D-Weinberg ’ 12 a], [Alaei al ’ 12], multitoetsingle[Cai-Huang’ 13] § “limited settings”: ► additive bidder reductions bidders and no allocation constraints ► unit-demand bidders and matroid constraints on who can be served

Setting paintings Previous Results OPT: [Cai-D-Weinberg STOC’ 12] (matroid) houses (matching) doctor appointments (downwards-closed) APPX: [A, BGGM, CHMS, KW] OPT: OPEN APPX: OPEN bridges OPT: OPEN

Challenge ► Revenue optimization in general multi-item settings. § ideally: (i) unified solution for all settings § (ii) Robustness of solutions to approximation, complexity.

A General Solution ► A generic reduction: § Mech. for Revenue Optimization Alg. for Welfare Optimization ► [Cai-D-Weinberg FOCS’ 12]: Suppose that: § bidder types are independent; § [the number of bidders m, items n, and the set-system allocations are unrestricted. ] of feasible then the revenue-optimal auction can be computed with queries to a welfare-optimization algorithm A for. ► The optimal auction has the following form: ► § § § bidders are asked to report their types; reported types are transformed into virtual types via bidder-specific functions; the virtual-welfare optimizing allocation in is chosen with a call to A; prices are charged to enforce truth-telling in Nash equilibrium. in Myerson’s theorem: virtual function = deterministic, closed-form here, randomized, computed during execution of Ellipsoid.

A General Solution ► A generic reduction: § Mech. for Revenue Optimization Alg. for Welfare Optimization ► [Cai-D-Weinberg FOCS’ 12]: Suppose that: § bidder types are independent; § [the number of bidders m, items n, and the set-system allocations are unrestricted. ] of feasible then the revenue-optimal auction can be computed with queries to a welfare-optimization algorithm A for. ► The optimal auction is a virtual welfare maximizer. ► Corollary: If the underlying welfare-maximization problem for is tractable (ignoring incentives), then so is the revenue-optimal auction. ►

Today’s menu General Auction Setting Background on Optimal MD Challenge, General Result Some Technical Ideas Combinatorial Optimization Viewpoint

Specifying an auction (explicit but expensive) ► via the ex-post allocation & price rule: : probability distribution over feasible sets from which allocation is chosen when bidders’ types are : price that bidder i pays under type profile ► ► ► description size: feasibility trivial to check (in fact hardwired into A) Folklore: can write LP on A and P to find a revenue-optimal auction why? expected revenue is linear in P, truthfulness constraints linear in A, P trouble: exponentially many variables § solving LP takes exponential time § solution is bad: “laundry-list” auction

Specifying an auction (lossy and still expensive) ► via the ex-post allocation probabilities: : marginal probability that item j is allocated to bidder i when bidders’ types are : price that bidder i pays when bidders’ types are description size still prohibitive: ► and feasibility is hard to check now efficiently: ► 1. is there a distribution over feasible allocations with these marginals, in view of the possibly combinatorial constraints on feasible allocations given by ? 2. bright exception: for simple allocation constraints, e. g. matching constraints, checking feasibility is easy using the Birkhoff-von Neumann theorem. ► can’t write LP anymore and, even if I could, its solution would be useless.

the reduced form of an auction ► a. k. a. the interim allocation & price rule : : marginal allocation probability of item j to bidder i when his type is ti (over the randomness in the other bidders’ types, and the randomness in mechanism) : expected price paid by bidder i when his type is ti (over the other bidders’ types, and the randomness in the mechanism) description size: ; ► c. f. description complexity of ex-post allocation rule ; ► feasibility hard to check: 1. Can the per-bidder marginal probabilities be reconciled? 2. …in a way that also respects the allocation constraints given by ? i. e. when can interim probabilities be converted to a feasible mechanism? ► wishful thinking: what if we could check feasibility efficiently? ►

Mechanism Design with the Reduced Form Variables: expected value of bidder i of type for being given (additivity of bidders) the reduced form of sought auction Constraints: Bayesian Nash Equilibrium: Objective: - the expected revenue - Need: (i) Separation oracle for feasible reduced forms - (ii) Efficient map from feasible reduced form to mechanism (optimal feasible reduced form is useless in itself)

feasibility of reduced forms

Feasibility of Interim Rules (example) easy setting: single item, two bidders with types uniformly distributed in T 1={A, B} and T 2={C, D} respectively ► allocation constraints = item cannot be given to more than one bidder ► Question: Are the following interim allocation probabilities feasible? ► bidder 1 ½ A ½ B so i ib s a e nf le ! C ½ bidder 2 D ½ whenever types are A, C: A needs to get item whenever types are A, D: A needs to get item type A satiated whenever types are B, C: C needs to get item type C satiated whenever types are B, D: B needs to get item with prob. 0. 4 and D needs to get item with prob. 0. 8

Feasibility of Interim Rules - Single-item reduced forms: - [Border ’ 91, Border ’ 07, CKM ’ 11]: Necessary and sufficient conditions. - linear constraints OR separation oracle w/ runtime - [Cai-D-Weinberg’ 12, Alaei et al ’ 12]: SO w/ runtime . . - Any hope for multi-item reduced forms, w/ arbitrary allocation constraints - [Cai-D-Weinberg FOCS’ 12 ]: Given black-box access to max-welfare algorithm for can decide feasibility of reduced-forms efficiently. Moreover, given feasible reduced form can efficiently find a mechanism with this reduced form. - the combinatorial optimization perspective - geometric view: ?

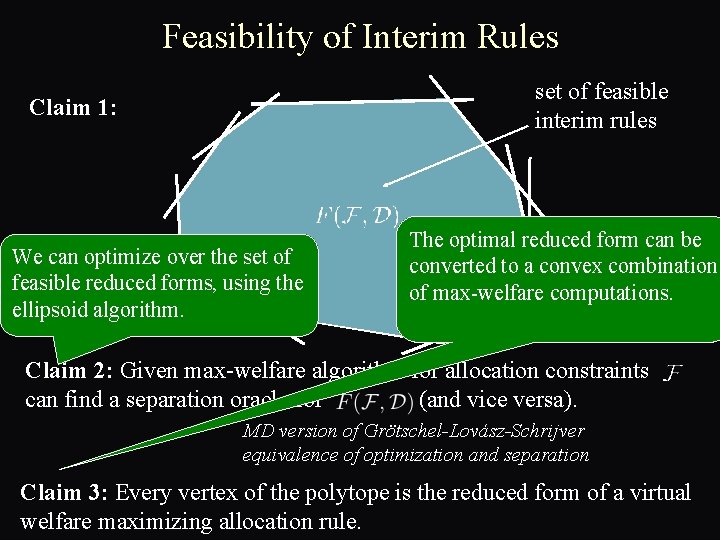
Feasibility of Interim Rules Claim 1: set of feasible interim rules Claim 2: Given max-welfare algorithm for allocation constraints can find a separation oracle for (and vice versa). MD version of Grötschel-Lovász-Schrijver equivalence of optimization and separation Claim 3: Every vertex of the polytope is the reduced form of a virtual welfare maximizing allocation rule.

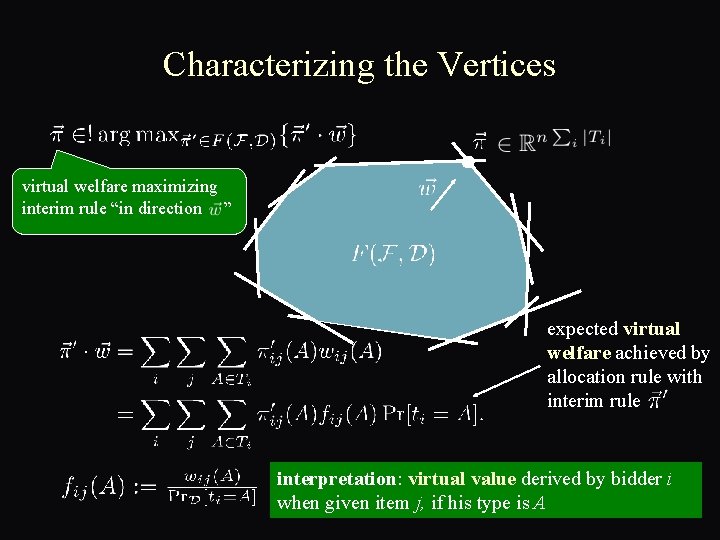
Characterizing the Vertices

Characterizing the Vertices virtual welfare maximizing interim rule “in direction ” expected virtual welfare achieved by allocation rule with interim rule interpretation: virtual value derived by bidder i when given item j, if his type is A

Characterizing the Vertices A virtual VCG allocation rule is defined by virtual functions , where , for all i. virtual welfare maximizing It takes a type-vector t 1, t 2, interim ruleas “ininput direction ” …, tm - transforms it into the virtual type-vector - then optimizes welfare using virtual types instead of true ones Q: OK understood what corner does, but what mechanism has this A: The VCG mechanism w/ virtual functions f 1, …, fm interpretation: virtual value derived by bidder i when given item j, if his type is A ?

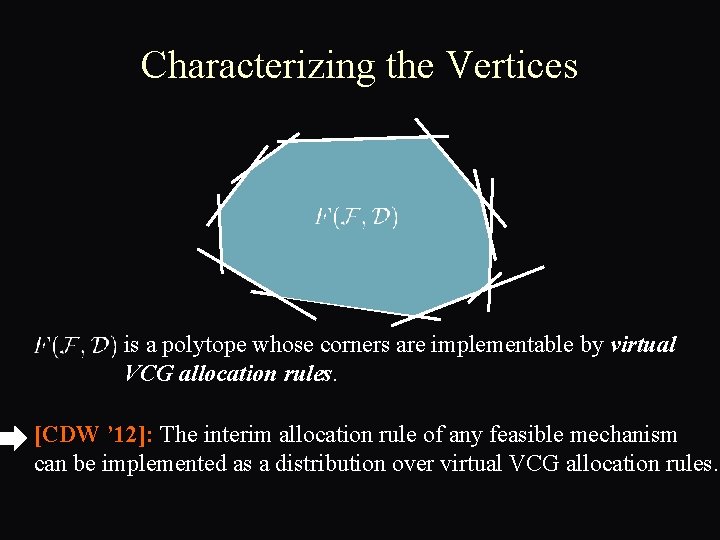
Characterizing the Vertices is a polytope whose corners are implementable by virtual VCG allocation rules. [CDW ’ 12]: The interim allocation rule of any feasible mechanism can be implemented as a distribution over virtual VCG allocation rules.

Feasibility of Interim Rules set of feasible interim rules Claim 1: We can optimize over the set of feasible reduced forms, using the ellipsoid algorithm. The optimal reduced form can be converted to a convex combination of max-welfare computations. Claim 2: Given max-welfare algorithm for allocation constraints can find a separation oracle for (and vice versa). MD version of Grötschel-Lovász-Schrijver equivalence of optimization and separation Claim 3: Every vertex of the polytope is the reduced form of a virtual welfare maximizing allocation rule.

Reality Check ► Connection to Grötschel-Lovász-Schrijver § Wishful thinking: given algorithm for welfare optimization under allocation constraints , can get linear optimization algorithm for. § Reality: Can’t do this efficiently; but can get additive-approx FPTAS. § Trouble: GLS requires exact linear optimization, and its extensions multiplicative approximations. § Solution: Specialized for MD. § Our result provides an extension of GLS to additive approximation algorithms, exploiting the structure of. ► End product: FPRAS § OPT-ε revenue, in time poly(1/ε). § [This still happens at BNE and not ε-BNE]

De-mystifying Myerson ► Unexpected properties of Myerson’s optimal single-item auction: § the auction is deterministic (no internal coin-flips) ; § while it is optimal among all auctions, it is itself a Dominant Strategy Truthful auction. ► Through our combinatorial optimization perspective we can easily show that § for all single-dimensional settings; and § for all objective functions that are linear in the interim rule (e. g. welfare, revenue, linear combinations thereof) the optimal auction is deterministic, DST, and a virtual welfare maximizer. ► Why? The optimal solution of the LP must be a corner. (No regularity assumption or ironing is needed for the argument. )

Summary ► Welfare optimization is a well-understood problem: § the VCG auction provides a reduction from mechanism to algorithm design ► The same is not true for revenue: § Myerson’s auction optimizes revenue in single-dimensional settings; § but multi-item settings are not well understood. ► I showed a general result providing the natural generalization of Myerson’s theorem to all multi-item settings. § “The revenue optimal auction is a virtual-welfare maximizer; which can be computed with polynomially many queries to a welfare-maximizing algorithm. ” ► Techniques: geometry, ellipsoid algorithm; § can optimize over reduced forms using welfare algorithm as a separation oracle.

Further Results/Open Problems ► Approximation Preserving reduction? § Given a-approximation for welfare, can obtain a-approximation for revenue? § Yes [Cai-D-Weinberg SODA’ 13]; § Complication: Can’t get separation oracle for polytope of reduced forms from approximation algorithm for welfare. size of support of bidder i’s type-distribution ► Implicit type-distributions? § our running-time is polynomial in ; § but suppose type-distribution is given implicitly ► e. g. consider additive bidder whose value for item j is uniform in {aj, bj} independently of other items § Q: can running time be improved for such implicit disn’s? § [D-Deckelbaum-Tzamos]: Problem is #P-hard even when there is a single additive bidder whose values are independent, rational, of support two. § But FPTAS still not precluded.

Further Results/Open Problems ► Nature of Virtual Functions § § ► both Myerson’s auction and its generalization are virtual welfare maximizers; Myerson provided a closed formula for each bidder’s virtual function; in the generalized auction, the virtual functions are computed by an algorithm; any structure for simple multi-item settings? Value Oracle Model? § in our work valuations in support are described explicitly; § what if valuations are implicit? ► i. e. given S, a circuit outputs value of bidder for subset S of items § Problem is NP-hard in general [Dobzinski-Fu-Kleinberg’ 11] § but what if valuations have structure? Thanks for listening