Part 1 Optimal MultiItem Auctions Constantinos Daskalakis EECS

Part 1: Optimal Multi-Item Auctions Constantinos Daskalakis EECS, MIT Reference: Yang Cai, Constantinos Daskalakis and Matt Weinberg: An Algorithmic Characterization of Multi-Dimensional Mechanisms, STOC 2012. http: //eccc. hpi-web. de/report/2011/172/

selling items Auctions spectrum allocation sponsored search § Motivating Question for Parts 1&2: Of all possible auctions, which one optimizes the auctioneer’s revenue? § We really mean “of all: ” want to choose the best among all possible protocols setting up a bidder interaction, in the end of which an allocation of items and pricing is decided.

Single-Item Auctions Optimal Auction? [Myerson’ 81]: The optimal single-bidder auction prices item at [Myerson’ 81]: Single item, multiple bidders whose values are i. i. d. from F: optimal auction is second price auction with reserve r(F). *

Myerson’s Auction [1981] 1 … i independent bidders … m [Myerson’ 81]: The optimal auction is a virtual welfare maximizer: 1. Collects bids b 1, …, bm from bidders 2. For all i: (i’s “ironed virtual bid”) 3. Allocates item to bidder with highest positive (if any) 4. Bidders are priced according to the “payment identity, ” ensuring that it’s in their best interest to report.

Beyond Single-Item Auctions? ► Large body of work in Economics: § e. g. [Laffont-Maskin-Rochet’ 87], [Mc. Afee-Mc. Millan’ 88], [Wilson’ 93], [Armstrong’ 96], [Rochet-Chone’ 98], [Armstrong’ 99], [Zheng’ 00], [Basov’ 01], [Kazumori’ 01], [Thanassoulis’ 04], [Vincent-Manelli ’ 06, ’ 07], [Figalli-Kim. Mc. Cann’ 10], [Pavlov’ 11], [Hart-Nisan’ 12], … ► Progress slow. No general approach. ► Challenge already with 1 bidder, 2 independent items. ? ? ? 1 2

Example 1: Two IID Uniform Items Obvious approach: - run Myerson for each item separately - price each item at 1 - each bought with probability 1 - expected revenue: 2 1 = 2 Optimal auction: - expected revenue: 3 ¾ = 2. 25 $3 The optimal mechanism need not sell items separately. Bundling items increases revenue.

Example 2: Two ID Uniform Items Optimal auction: $4 This item with probability ½ $2. 50 - expected revenue: $2. 625 The optimal mechanism may not only bundle items, but also use randomization.

Beyond Single-Item Auctions? ► Large body of work in Economics: § e. g. [Laffont-Maskin-Rochet’ 87], [Mc. Afee-Mc. Millan’ 88], [Wilson’ 93], [Armstrong’ 96], [Rochet-Chone’ 98], [Armstrong’ 99], [Zheng’ 00], [Basov’ 01], [Kazumori’ 01], [Thanassoulis’ 04], [Vincent-Manelli ’ 06, ’ 07], [Figalli-Kim. Mc. Cann’ 10], [Pavlov’ 11], [Hart-Nisan’ 12], … ► Progress slow. No general approach. ► Challenge already with 1 bidder, 2 independent items. ► Recent algorithmic work: Constant Factor Approximations ► [Chawla-Hartline-Kleinberg ’ 07], [Chawla et al’ 10], [Bhattacharya et al’ 10], [Alaei’ 11], [Hart-Nisan ’ 12], [Kleinberg-Weinberg ’ 12]

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Multi-item Auctions Computational Remarks

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Multi-item Auctions Computational Remarks

Multi-item Auctions 1 1 … … j i … … m maximize revenue n - Bidders are additive (for Part 1) - each bidder i is characterized by some vector - his value for subset S of items is: - Bayesian assumption: bidder types (t 1, …, tm) drawn from product distn’ ’ s are known is supported on set Ti which is assumed finite - INPUT: m, n, T 1, …, Tm , - GOAL: Find auction optimizing revenue.

Auction in Action 1 1 … … j i Auctioneer: … … - Commits to an auction design, specifying possible bidder actions, the allocation and the price rule - Asks bidders to choose actions expected revenue: m n - Implements the promised allocation payment and price rule made by bidder to the auctioneer - Goal: i. Optimize revenue over bidder types t 1, …, tm, the randomness in the auction (if any), and Each Bidder i: the her randomness - Uses as input: the auction specification, own typeinti the andbidders’ strategic behavior given their types - Chooses action - Goal: optimize her own utility Bayesian Nash Equilibrium

► Simplification: Direct Auctions Focus on Direct Auctions (wlog) § huge universe of possible auctions: what bidders can do, and how to allocate items and charge bidders when they do it § The direct revelation principle: “Any auction has an equivalent one where the bidders are only asked to report their type to the auctioneer, and it is best for them to truthfully report it. Such auctions are called direct. ” § equivalent ? ► point-wise w. r. t. : the two auctions result in the same allocation, the same the auction’s ex-post payments, and the same called bidder utilities § upshot: allocation and price rule ► mechanism design reduces to computing functions: : probability (over randomness in auction) that item j is allocated to bidder i when the reported types by bidders are : expected price that bidder i pays when reports are

Finding Optimal Direct Auction ► Find ► Such that: ► 1. Feasible: 2. It is in every bidder’s “best interest” to truthfully report his type. ► Captured by Bayesian Incentive Compatibility (BIC) constraint: § for all i, and types : 3. The expected revenue is maximized Actually an LP, but of the “laundry-list” kind… § number of variables: vs input size

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Multi-item Auctions Computational Remarks

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Multi-item Auctions Computational Remarks

the interim rule of an auction ► a. k. a. the reduced form : : probability item j is allocated to bidder i conditioning on his type being ti (over the randomness in the other bidders’ types, and the randomness in the auction) : expected price paid by bidder i conditioning on his type being ti ► Example: Suppose 1 item, 2 bidders bidder 1 ½ A C ½ ½ B D ½ bidder 2 Consider auction that allocates item preferring A to C to B to D, and charges $2 dollars to whoever gets the item. ► Then ►

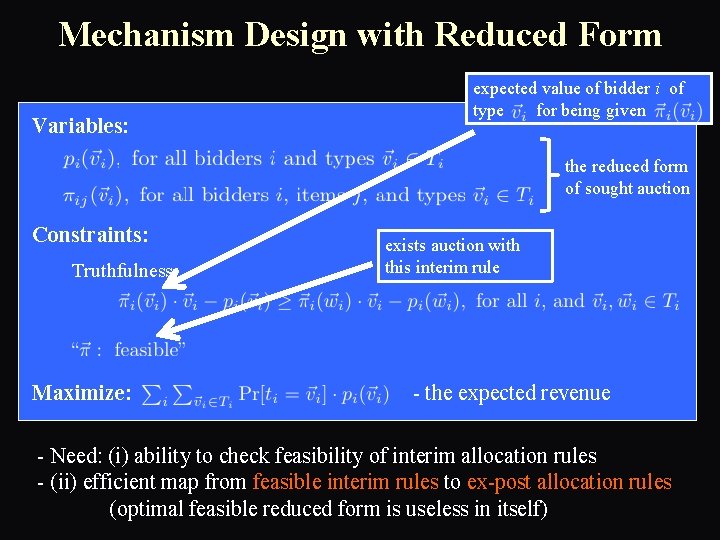
Mechanism Design with Reduced Form Variables: expected value of bidder i of type for being given the reduced form of sought auction Constraints: Truthfulness: Maximize: exists auction with this interim rule - the expected revenue - Need: (i) ability to check feasibility of interim allocation rules - (ii) efficient map from feasible interim rules to ex-post allocation rules (optimal feasible reduced form is useless in itself)

Feasibility of Reduced Forms (example) easy setting: single item, two bidders with types uniformly distributed in T 1={A, B, C} and T 2={D, E, F} respectively ► Question: Is the following interim allocation rule feasible? ► bidder 1 ⅓ A ⅓ B ⅓ ! e l b si a fe n i o s C ( A, D/E/F) A wins. (B/C, D) D wins. D ⅓ E ⅓ F ⅓ ✔ ✔ (B, F) B wins. (C, E) E wins. (B, E) B needs to win w. p. ½, E needs to win w. p. ⅔ bidder 2

Feasibility of Reduced Forms ► ► ► [Border ’ 91, Border ’ 07, Che-Kim-Mierendorff ’ 11]: Exist linear constraints characterizing feasibility of single-item reduced forms. Problem: Single-item, and exponentially many inequalities. [Cai-Daskalakis-Weinberg’ 12]: -many inequalities suffice. ([Alaei et al’ 12]: polynomial-time algorithm for feasibility) Still only single-item reduced forms.

Feasibility of Multi-Item Reduced Forms ► Can view ► Denote feasible interim allocation rules by ► How does look geometrically?

Feasibility of Multi-Item Reduced Forms Claim 1: ► set of feasible interim allocation rules Proof: Easy. § If feasible, exists (ex-post) allocation rule M with interim rule. § M is a distribution over deterministic feasible allocation rules, of which there is a finite number. So: , where is deterministic. § Easy to see: § So

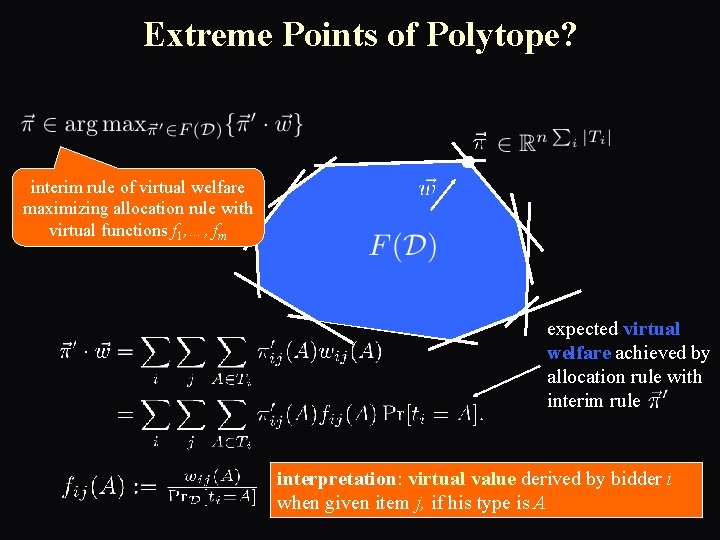
Extreme Points of Polytope?

Extreme Points of Polytope? interim rule of virtual welfare maximizing allocation rule with virtual functions f 1, …, fm expected virtual welfare achieved by allocation rule with interim rule interpretation: virtual value derived by bidder i when given item j, if his type is A

Feasibility of Multi-Item Reduced Forms Claim 1: set of feasible interim allocation rules Any interim rule is implementable by a convex combination of (i. e randomization over) virtual-welfare maximizers. Claim 2: Every vertex of the polytope is the interim rule of a virtual welfare maximizing allocation rule for some virtual functions f 1, …, fm.

An Example 1 item, 2 bidders, each with uniform type in {A, B} ► consider following (somewhat funky) allocation rule M: ► § If types are equal, give item to bidder 1 § Otherwise, give item to bidder 2 Can M be implemented as a distribution over virtual-welfare maximizing allocation rules? ► A: No ► § Proof: Suppose M was distn’ over virtual welfare max. alloc. rules. § If reported types are (t 1=A, t 2=A), or (t 1=B, t 2=B) then bidder 1 gets the item with probability 1. § So all virtual welfare maximizing allocation rules in the support of the distn’ have virtual value functions f 1 and f 2 satisfying: ► f 1(A)>f 2(A) and f 1(B)>f 2(B). (*) ► f 2(A)>f 1(B) and f 2(B)>f 1(A). (**) can’t hold § Likewise, all virtual rules in the support need to satisfy: simultaneously

An Example 1 item, 2 bidders, each with uniform type in {A, B} ► consider following (somewhat funky) allocation rule M: ► § If types are equal, give item to bidder 1 § Otherwise, give item to bidder 2 ► ► ► Can M be implemented as a distribution over virtual-welfare maximizing allocation rules? A: No OK, what’s the interim rule of M? A: Can this be implemented as a distribution over virtual-welfare maximizing allocation rules? A: yes, use the following distn’ over virtual functions f 1, f 2: § f 1(A)=f 1(B)=1, f 2(A)=f 2(B)=0, w/ prob. ½ § f 1(A)=f 1(B)=0, f 2(A)=f 2(B)=1, w/ prob. ½

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Optimal Multi-item Auctions Computational Remarks

Mechanism Design with Reduced Form Variables: the reduced form of sought auction Constraints: Truthfulness: Maximize: - the expected revenue Two auctions with same interim allocation rule have same revenue

Characterization of Optimal Multi -Item Auctions ► [Cai-Daskalakis-Weinberg’ 12]: For every multi-item auction, there exists an auction with the same interim rule, which is a distribution over virtual welfare maximizers. ► Corollary: Optimal multi-item auction has the following structure: Bidders submit types (t 1, …, tm) to auctioneer. ► Auctioneer samples virtual transformations f 1, …, fm ► Auctioneer computes virtual types ► Virtual welfare maximizing allocation is chosen. ► § Namely, each item is given to bidder with highest virtual value for that item (if positive) ► Prices are charged to ensure truthfulness

Characterization of Optimal Multi -Item Auctions Bidders submit types (t 1, …, tm) to auctioneer. ► Auctioneer samples virtual transformations f 1, …, fm ► Auctioneer computes virtual types ► Virtual welfare maximizing allocation is chosen. ► § Namely, each item is given to bidder with highest virtual value for that item (if positive) ► Prices are charged to ensure truthfulness ► Exact same structure as Myerson ►in Myerson’s theorem: virtual function = deterministic ►here, randomized (and they must be)

The Menu Motivation Multi-Item Auction Setting Auctions from Linear Programs -the interim allocation rule Characterization of Optimal Multi-item Auctions Computational Remarks

Mechanism Design with Reduced Form Variables: the reduced form of sought auction Constraints: Truthfulness: Maximize: - the expected revenue - To solve need: (i) ability to check feasibility of interim allocation rules - (ii) efficient map from feasible interim rules to ex-post allocation rules (optimal feasible reduced form is useless in itself)

Poly-time Feasibility and Implementation Need separation oracle for: [Grötschel-Lovász-Schrijver ’ 80/Papadimitriou-Karp’ 80]: Linear Optimization Separation What this means for us is: suffices to be able to find in polynomial-time, the extreme interim allocation rule in an arbitrary direction. ✔ But we know that is virtual welfare maximizer for some f 1, f 2, …, fm Hence: Can be found in polynomial time.

Mechanism Design with Reduced Form Variables: the reduced form of sought auction Constraints: Truthfulness: Maximize: - the expected revenue - To solve need: (i) ability to check feasibility of interim allocation rules ✔ - (ii) efficient map from feasible interim rules to ex-post allocation rules ✔ (optimal feasible reduced form is useless in itself)

Summary Compared to Single-Item auctions, optimal multi-item auctions: § have richer structure § are computationally more challenging ► Understanding Interim allocation rule allowed us to characterize the structure of optimal multi-item auctions for additive bidders: § “The revenue optimal auction is a virtual-welfare maximizer. ” § Difference to Myerson: virtual transformation randomized. ► Finding Optimal Auction: polynomial-time solvable ► ► Up next: § Yang: Beyond additive bidders/trivial allocation constraints § Matt: Beyond revenue objective