Optimal Auctions Through Deep Learning Paul Dtting Zhe

Optimal Auctions Through Deep Learning Paul Dütting, Zhe Feng, Harikrishna Narasimhan, David C. Parkes Presented by Efrat Vinker

Agenda • Introduction • The Regret. Net Framework • • The Learning Problem Optimization - Augmented Lagrangian Solver Neural Network Architecture Evaluation • The Rochet. Net Framework • The characterization of Rochet for a single bidder problem • Neural Network Architecture • Evaluation • Summary

Introduction • Goal: • Approach: Designing an incentive compatible auction that maximizes expected revenue Multi-layer neural networks to encode auction mechanism, with bidder valuations being the input and allocation and payment decisions being the output • Regret. Net • Rochet. Net (Characterization-Based Approach)

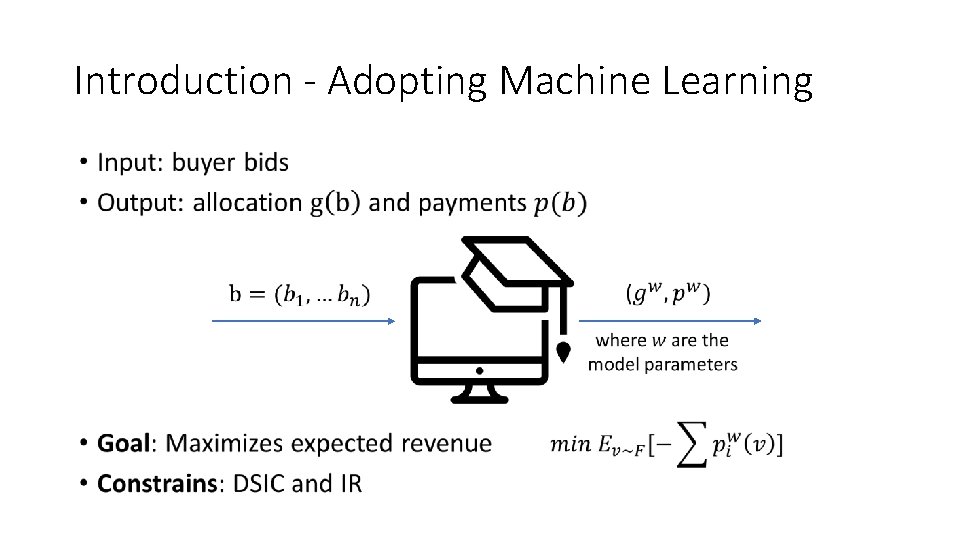
Introduction - Adopting Machine Learning •

Introduction •

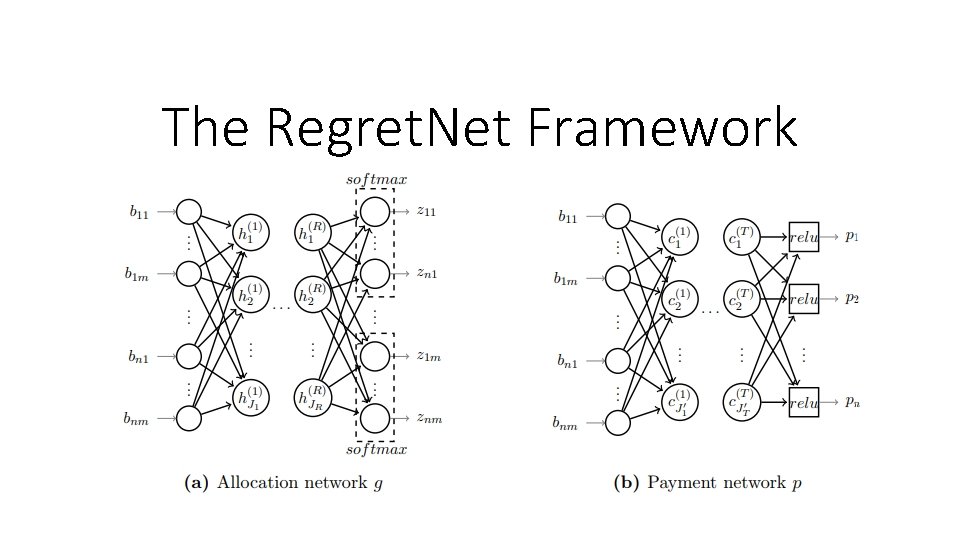
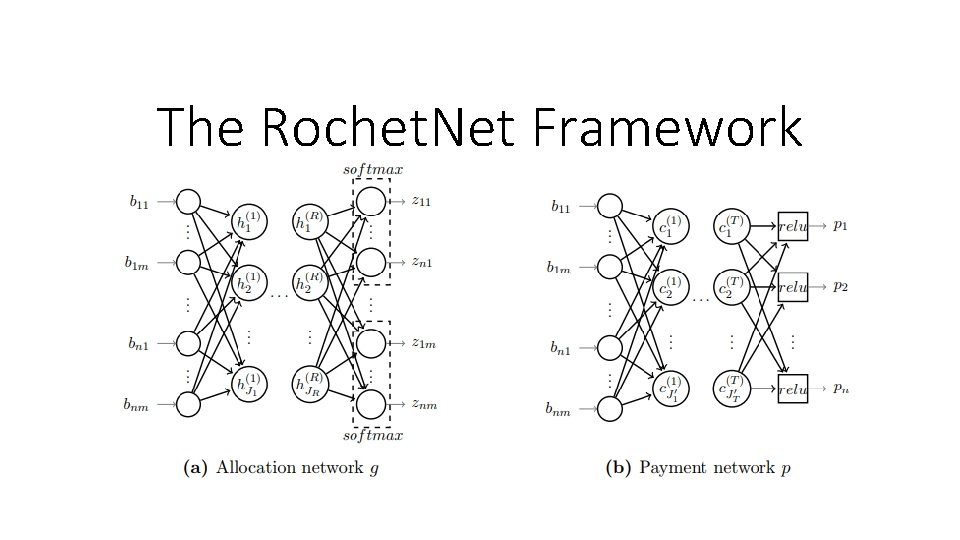
The Regret. Net Framework

Formulating Constraints for DSIC and IR •

Formulating Constraints for DSIC and IR •

Formulating Constraints for DSIC and IR • The learning problem: • Re-formulate the learning problem:

Formulating Constraints for DSIC and IR •

Formulating Constraints for DSIC and IR

Augmented Lagrangian Method • Consider an optimization problem with s equality constraints: • The Augmented Lagrangian method formulates an unconstrained objective, involving the Lagrangian for the problem, augmented with additional quadratic penalty terms that penalize violations in the equality constraints:

Augmented Lagrangian Method •

Augmented Lagrangian Method • The gradient is pushed through the loss function as well as an empirical measure of regret

Recap • The Regret. Net Framework: • The learning problem • The Augmented Lagrangian solver

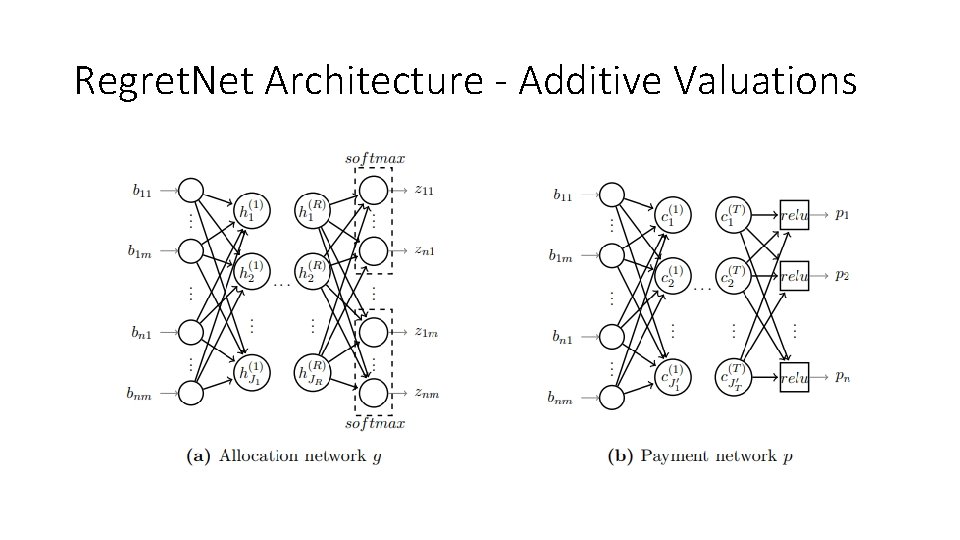
The Regret. Net Architecture let's look deeper !

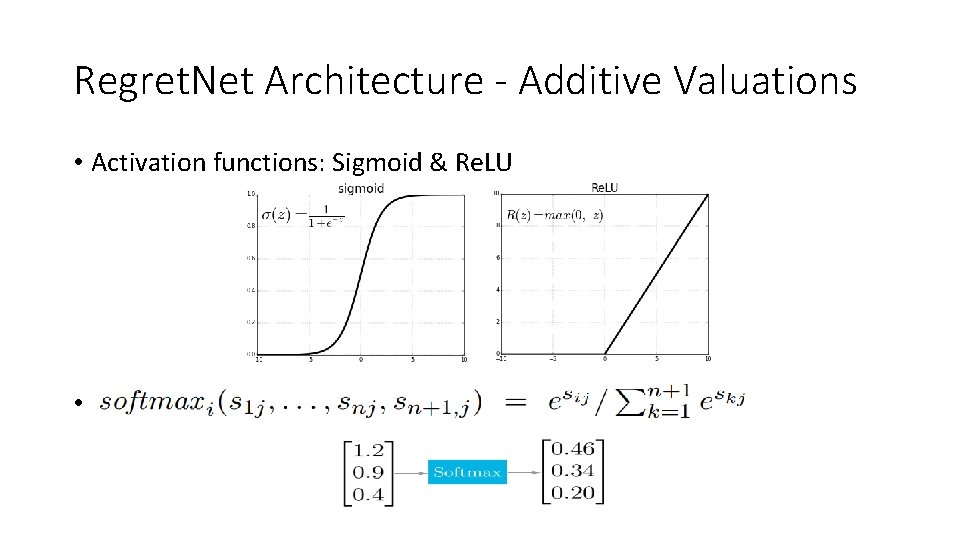
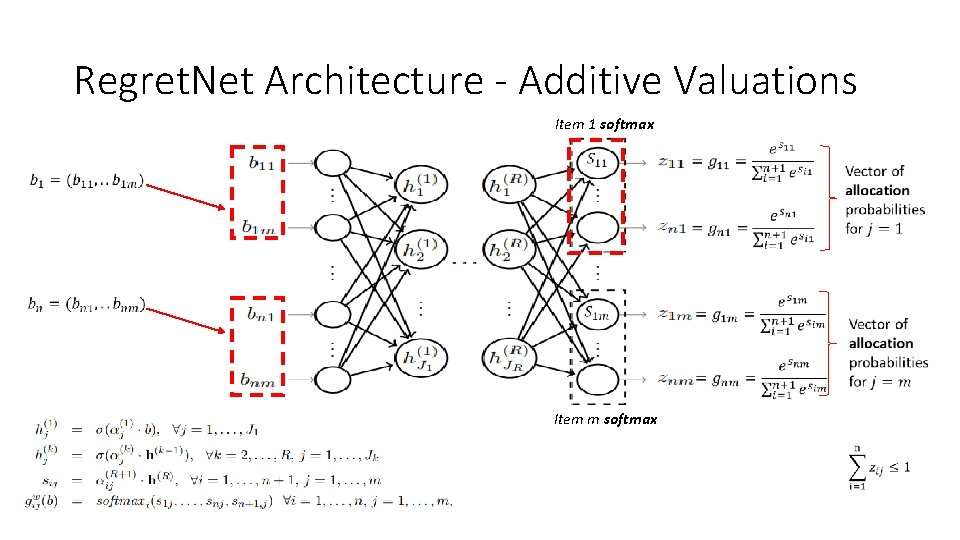
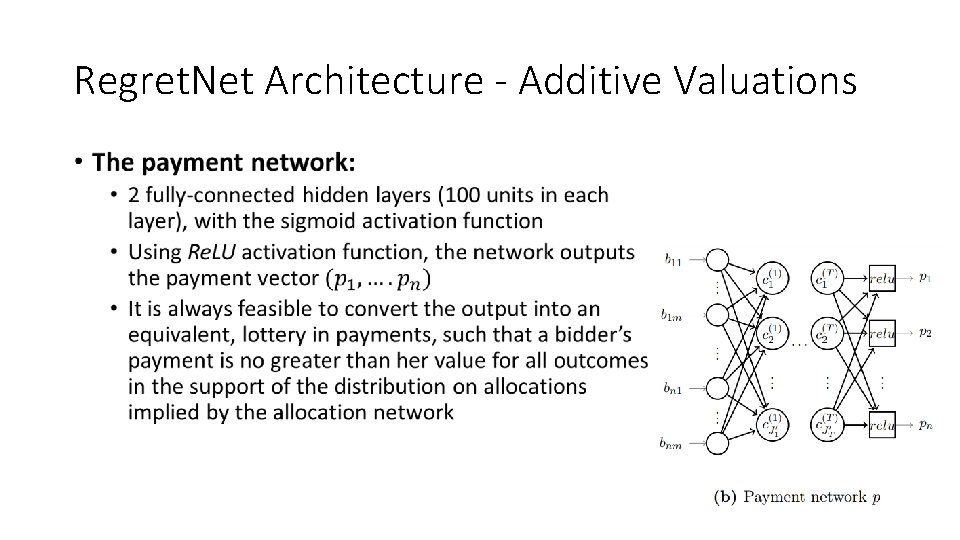
Regret. Net Architecture - Additive Valuations • Activation functions: Sigmoid & Re. LU •

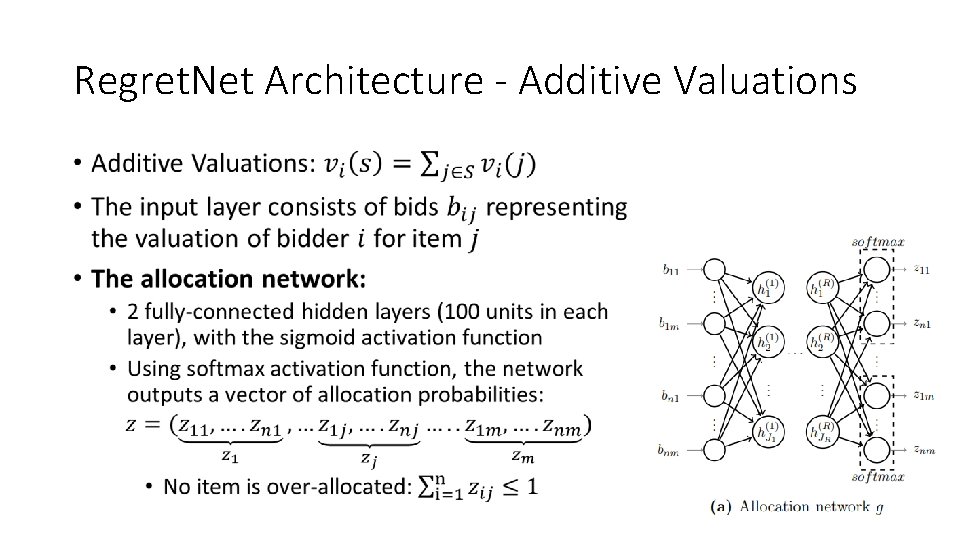
Regret. Net Architecture - Additive Valuations •

Regret. Net Architecture - Additive Valuations Item 1 softmax Item m softmax

Regret. Net Architecture - Additive Valuations •

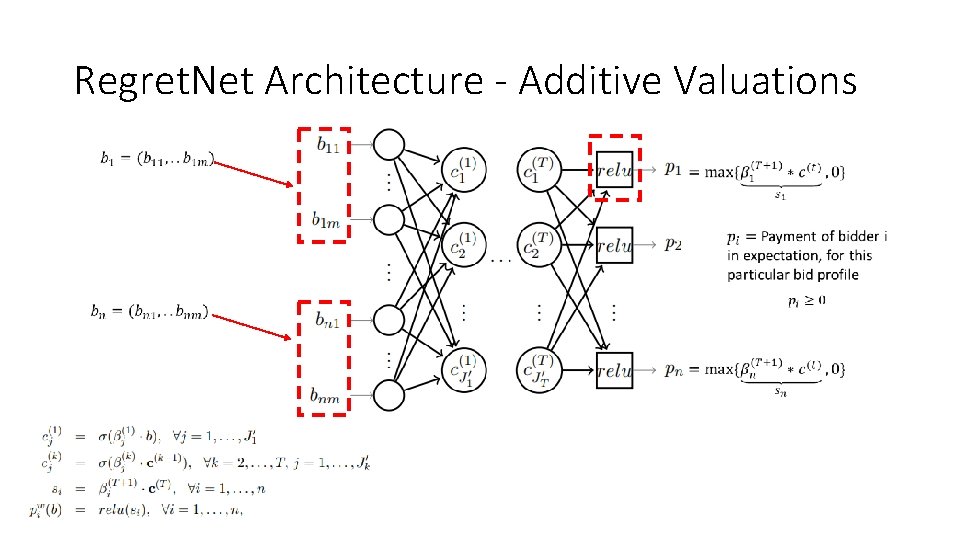
Regret. Net Architecture - Additive Valuations

Regret. Net Architecture - Additive Valuations

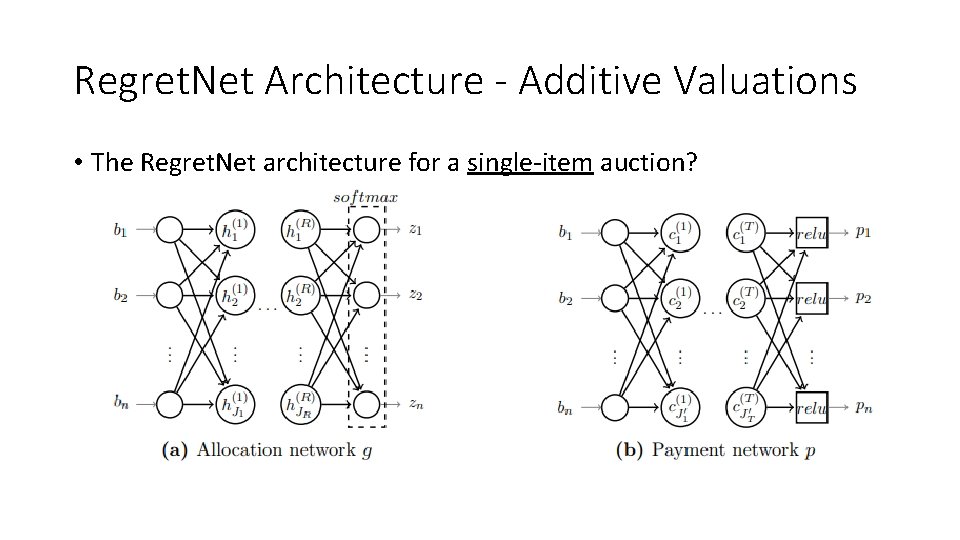
Regret. Net Architecture - Additive Valuations • The Regret. Net architecture for a single-item auction?

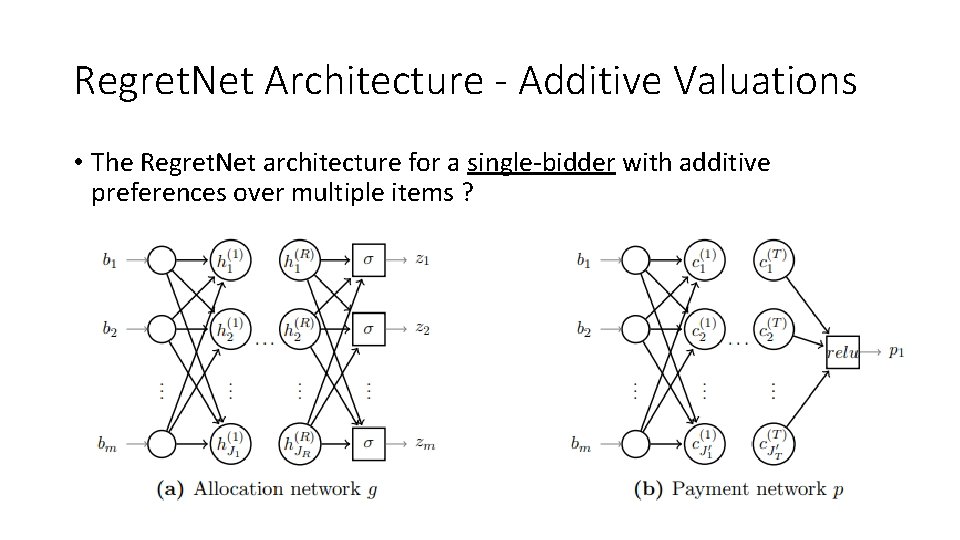
Regret. Net Architecture - Additive Valuations • The Regret. Net architecture for a single-bidder with additive preferences over multiple items ?

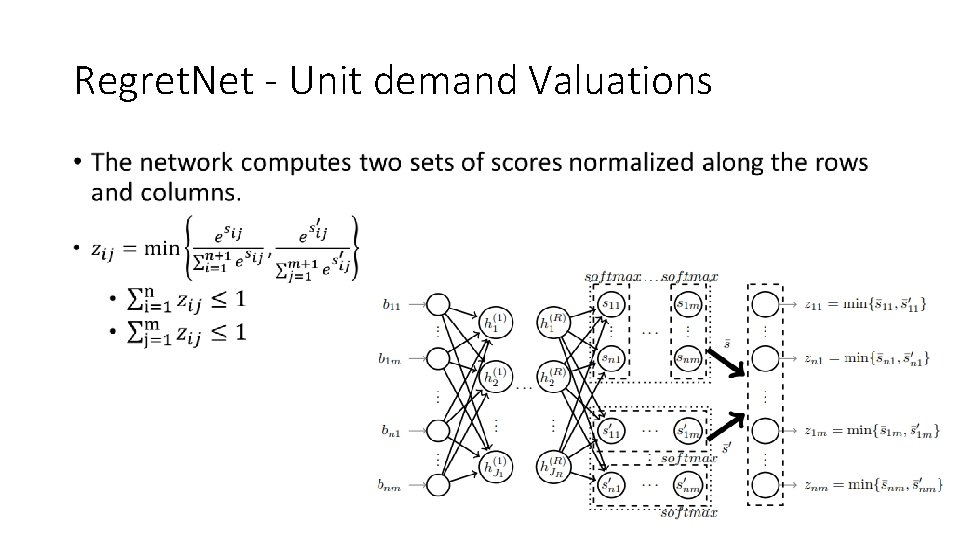
Regret. Net - Unit demand Valuations •

Regret. Net - Unit demand Valuations •

Regret. Net – Combinatorial Valuations •

Regret. Net – Combinatorial Valuations •

Recap • The Regret. Net Framework: • The learning problem • The Augmented Lagrangian solver • Regret. Net Architecture: • Additive Valuations • Unit demand Valuations • Combinatorial Valuations - if time permits

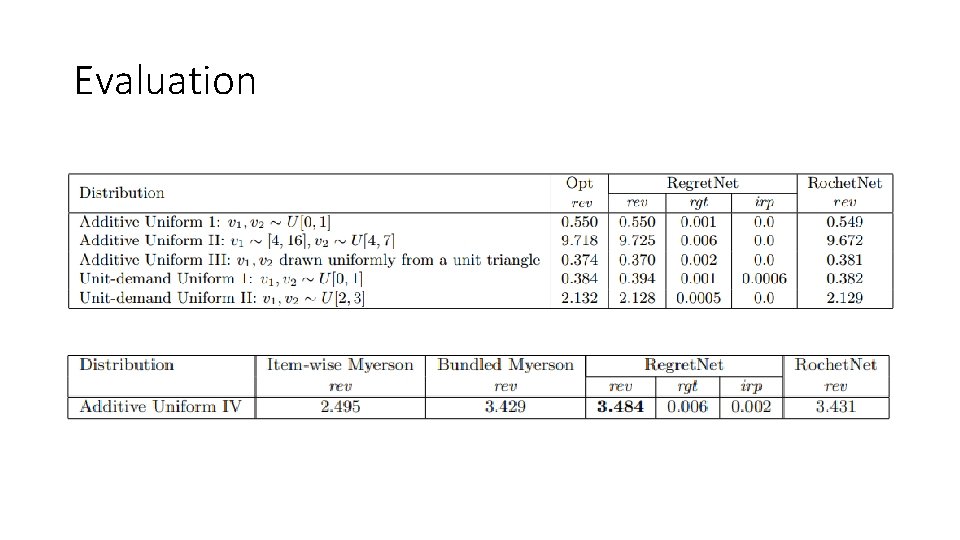
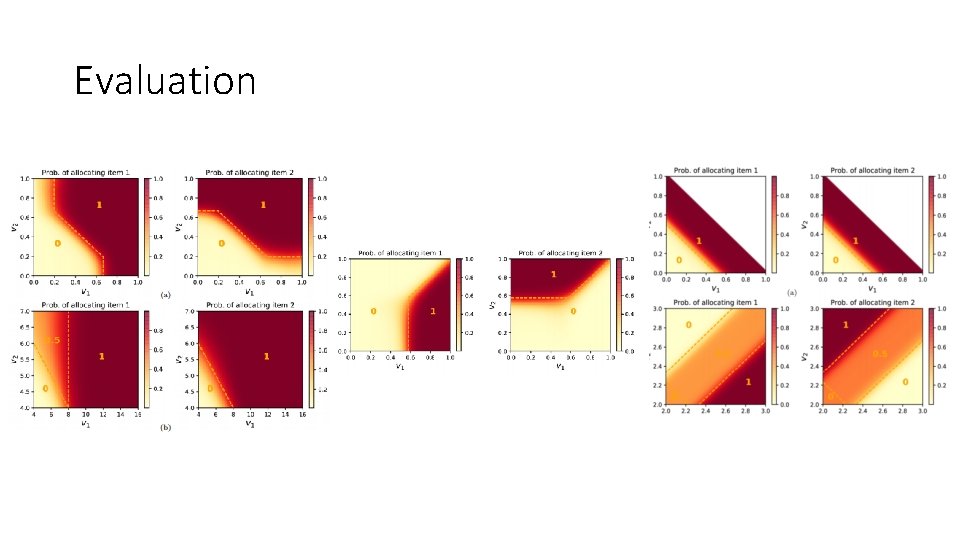
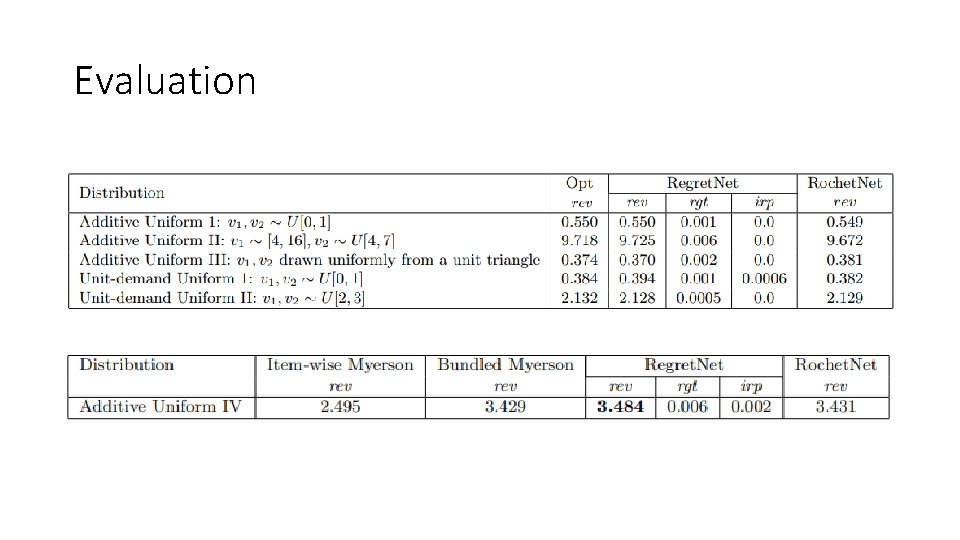
Evaluation

Evaluation

Evaluation

The Rochet. Net Framework

The Rochet. Net Framework • Achieves DSIC by hard-coding known characterization results into the network architecture • Use neural networks to search over a specific class of fully-DSIC mechanisms that are known to contain the optimal auction • Setting: single bidder • (-) Less general, as a result of its appeal to characterization results • (+) A tool to test conjectures about the structure of optimal auctions in poorly-understood settings

The Rochet. Net Framework •

The Rochet. Net Framework •

The Rochet. Net Framework •

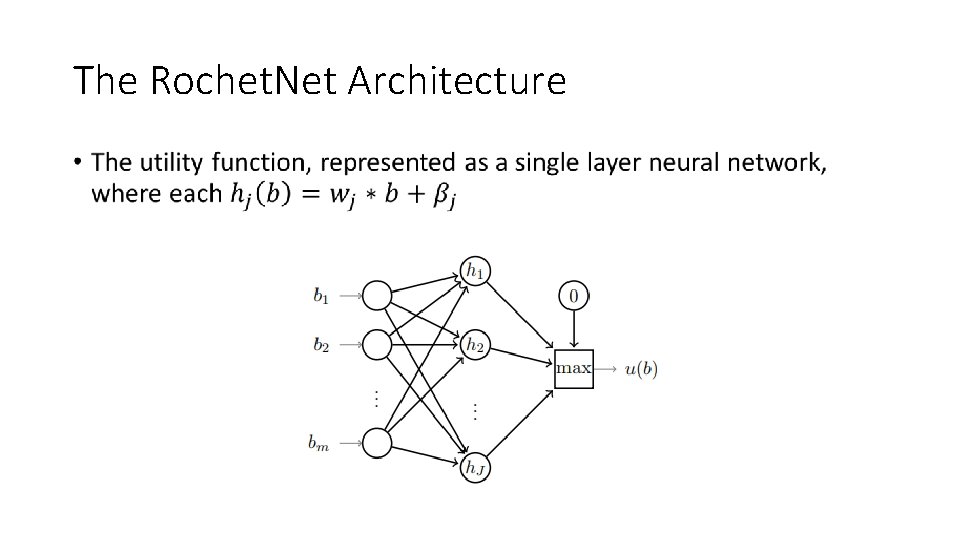
The Rochet. Net Architecture •

The Rochet. Net Architecture •

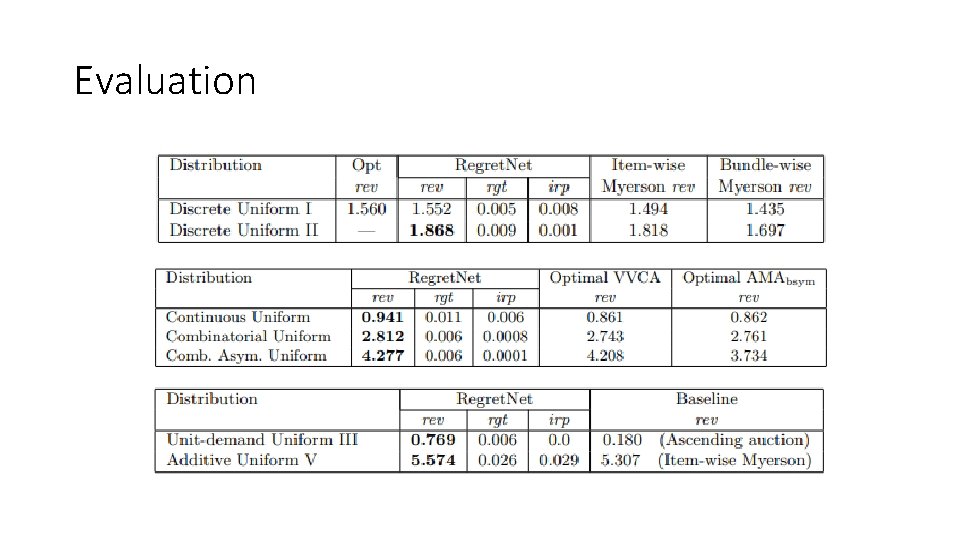
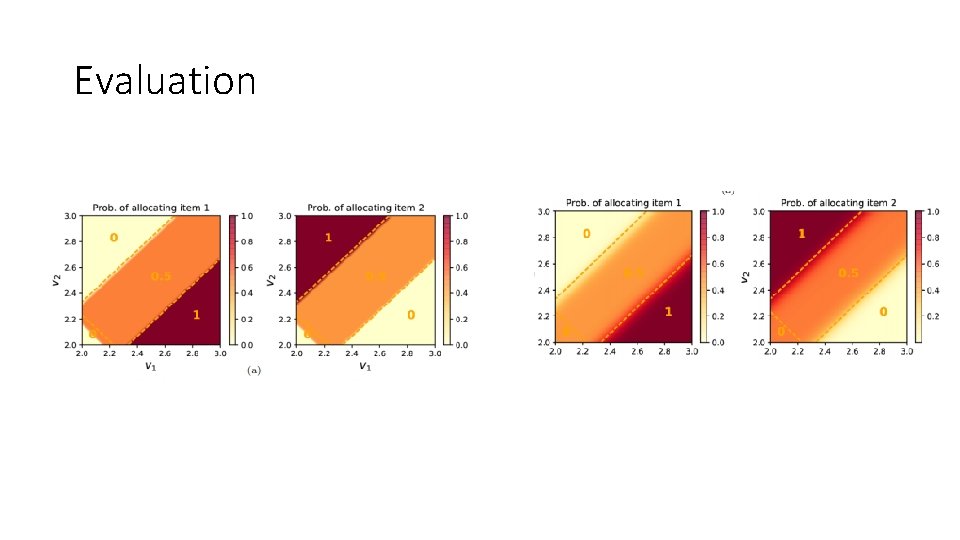
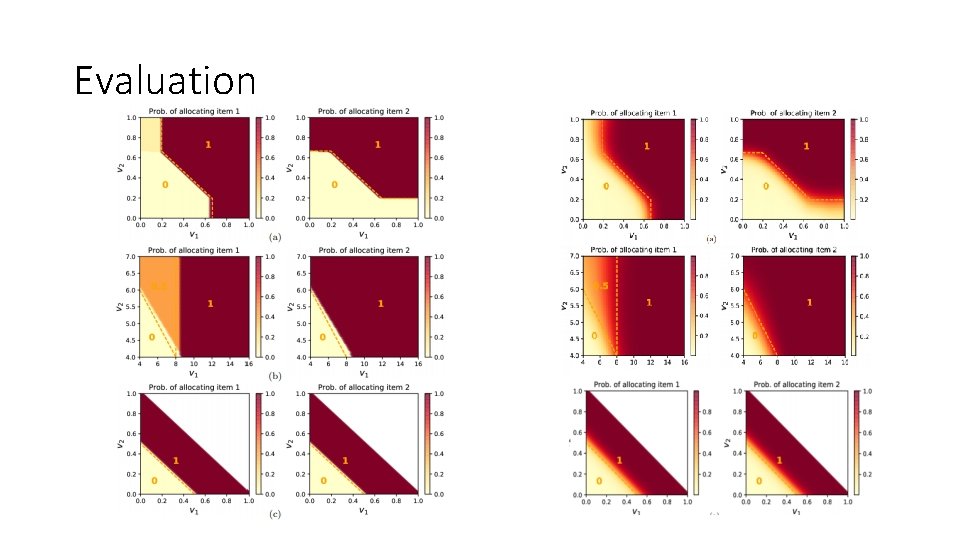
Evaluation

Evaluation

Evaluation

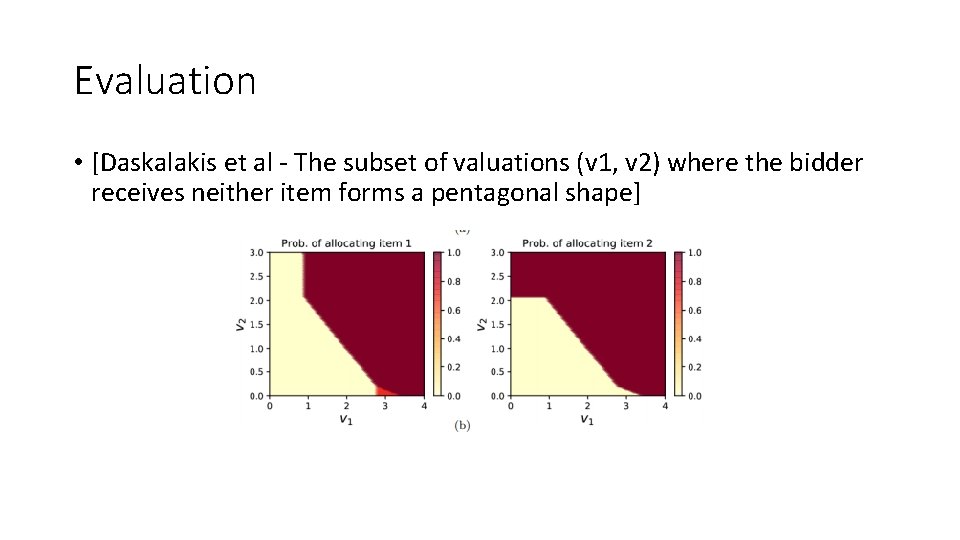
Evaluation • [Daskalakis et al - The subset of valuations (v 1, v 2) where the bidder receives neither item forms a pentagonal shape]

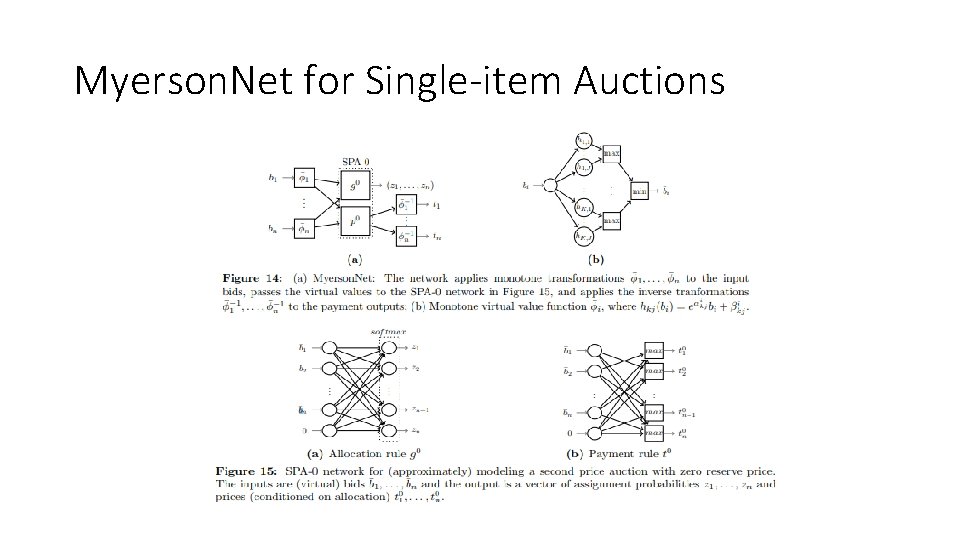
Myerson. Net for Single-item Auctions

Summary • The Regret. Net Framework: • • Formulating constraints for DSIC and IR Augmented Lagrangian Solver Different architecture for each valuation type Network output: allocation and payment • The Rochet. Net Framework: • Single bidder • Achieves DSIC by hard-coding known characterization results into the network architecture • Search over a specific class of DSIC mechanisms that are known to contain the optimal auction

Summary • The work demonstrates the potential of applying deep learning in the context of economic design • The approach is capable of recovering essentially all analytical solutions for multiitem settings that have been obtained over the past 30 -40 years by finding auctions with almost optimal revenue and vanishingly small regret that match the allocation and payment rules of theoretically optimal auctions to surprising accuracy. • The approach finds high-revenue auctions with negligibly small regret in settings in which the optimal auction is unknown (the combinatorial settings), matching or outperforming state-of-the-art computational results [Sandholm and Likhodedov, 2015]. • The approach learns auctions for larger settings, such as a 5 bidder, 10 items setting, where optimal auctions have been to hard to design, and finds low regret auctions that yield higher revenue than strong baselines