Multiitem auctions with identical items limited supply M

Multi-item auctions with identical items • limited supply: M items (M smaller than number of bidders, n). • Three possible bidder types: – Unit-demand bidders – Decreasing marginal values – General valuations – We only consider private values • We will see both strategic considerations and computational considerations.

Unit demand bidders • Each bidder desires one item. • Two popular “sealed-bid” auction formats: – Uniform-price auctions: The M highest bidders win, each pays the M+1 highest bid. – Discriminatory auctions: The M highest bidders win, each pays her bid. • Two equivalent “open-cry” auctions: – Ascending price (English): The price ascends until M bidders remain. – Descending price (Dutch): The price descends until M bidders accept. • Similarly to the single-item case, uniform-price is equivalent to English, and Discriminatory price is equivalent to Dutch.

Efficiency and Revenue in Unit-Demand • Uniform-price is in fact a VCG mechanism (check at home). Therefore: – Truth-telling is a dominant strategy – The resulting allocation is efficient • Discriminatory-price with symmetric bidders has a symmetric efficient equilibrium (similar analysis to the first-price auction). • The revenue equivalence theorem and the optimal auction analysis can be extended to unit-demand bidders: – Any two auctions with the same outcome in equilibrium raise the same revenue (e. g. unifrom-price and discriminator-price). – The optimal auction is to sell the M items to the M bidders with the highest marginal valuations.

Example “Real” Applications • Government securities were sold by the US government using discriminatory auctions, until 1992. • From 1992, some securities (e. g. 2 -years and 5 -years) are being sold using a uniform-price auction. • In the UK, electricity generators bid to sell their output on a daily basis. Until 2000 the auctions were uniform-price, and after that they switched to discriminatory price

Decreasing Marginal Valuations • Each player has a marginal valuation function vi: {1, …, M}-> R – The value of receiving q items is vi(1)+…+vi(q) • Marginal decreasing means: vi(q+1) < vi(q) for any 1<q<M • Implication: Every bidder submits many bids • Example for the uniform-price auction with two items: Red is player 1 17 Black is player 2 15 14 Result: the red player wins two items 7 and pays 2· 14=28 => utility=4 6 Observation: if the red player only bids 17 then he will win one item and will pay price=6, increasing his utility!

Conclusions and remarks • It is no longer true that the dominant strategy of a player in the uniform-price auction is to bid truthfully. – Therefore uniform-price in this case is different than VCG. • As we saw, it is beneficial for the players to decrease their stated values for the items. This phenomena is termed “demand reduction”. • There are no dominant strategies. However, the uniform-price auction is known to have a pure strategy equilibrium, in which: – “demand reduction” occurs. – the result is inefficient. • It is also possible to show that every equilibrium of the discriminatory auction is inefficient.

VCG • VCG continues of-course to have dominant strategies and an efficient outcome. • The VCG price for this case: suppose player i won q items, and let x 1, …, xq be the q highest non-winning bids of the other players. Then player i pays x 1+…+xq. – Recall that in general the price is -Σj≠i vi(a) + Σj≠i vi(b), where a is the allocation chosen when i participates and b is the allocation chosen when i does not participate. • In the previous example (2 -item auction), 17 15 Result: the red player wins two items 14 and pays 14+6=20 => utility=12 7 6

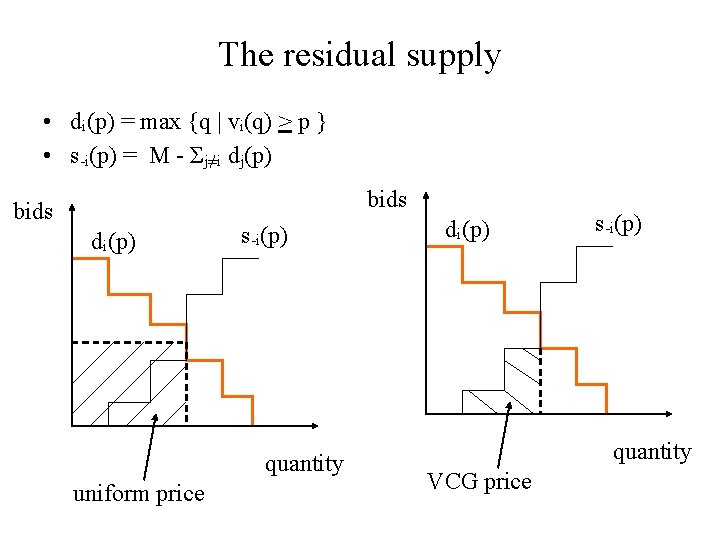
The residual supply • di(p) = max {q | vi(q) > p } • s-i(p) = M - Σj≠i dj(p) bids di(p) s-i(p) quantity uniform price di(p) s-i(p) quantity VCG price

The Ausubel auction • An ascending auction that is equivalent to VCG: – We start with a very low price (at this point s-i(p)=0). – The price is raised until, for at least one player i, s-i(p)>0. – Every player i gets s-i(p) units, for a price-per-unit p. – Continue in the same manner. • The residual supply of i increases exactly at the marginal value of some other player, i’, for one of his units (say q). This means that this other player i’ will win at most q-1 units. • Therefore, player’s price exactly equals the marginal value of the others for the units he got. • As a result, truthfulness is an ex-post equilibrium in this auction.

Example • 1’s bid: 17, 15, 7. 2’s bid: 14, 6. • While price < 6, the demand of both players is at least two, so the residual supply < 0. • At a price=6, 2’s demand decreases to 1. Therefore 1’s residual supply is 1, so he gets one unit. • At price=14, 2’s demand decreases to 0, and 1 gets another unit.

General valuations (with complementarities) • In general, marginal valuations may increase. For example v(1)=0, v(2)=100 represents a situation where the player must get two units in order to obtain any value from the items. – Let Vi(q) denote the total value of player i for q items. We still assume that Vi(q) < Vi(q+1) (“free disposal”). • In this case, the discriminatory-price and the uniform-price have no real meaning. • VCG, again, has dominant strategies, and reaches the efficient outcome. However, no “natural” way of representing VCG or its price is known. We simply use the general mechanism.

Computational issues • How do we compute the optimal allocation? • Solve with dynamic programming: – O(i, q) = the optimal welfare for players 1, …, i, obtained with q items. – O(i, q)=maxq’<q { O(i-1, q’) + Vi(q-q’) } • We need at most (an order of) M operations to compute every O(i, q), and so in total we need an order of n·M 2 operations to compute O(n, M), which is what we need. • Sometimes M is extremely large (tens of thousands of items), and we want faster algorithms. It is known that it is impossible to achieve the exact optimum in a faster way, but can we design truthful approximation auctions?

Truthful approximations • To achieve truthfulness with the VCG method, we must choose the alternative with the maximal welfare. But we can restrict the alternatives as we wish! • A faster VCG mechanism: – Bundle the items in n 2 bundles of size b = M/n 2 , and one “remainder” bundle of size r such that M=b·n 2 + r. – Allocate items only in bundles, i. e. each player can receive a multiple of b items, or the entire set of items. – Ask the players for their values of all these possible n 2+1 bundles, and find the allocation with maximal welfare among all these allocations.

Example • n=2, M=100. The values are: – Player 1: v 1(12)=10, v 1(64)=23, v 1(80)=30, and all the rest are the minimal possible. – Player 2: v 2(26)=15, v 2(36)=20, v 2(40)=22, and all the rest are the minimal possible. • players can get only multiples of M/n 2=25. Therefore we ask each player for his value for 25 items, 50 items, 75 items, and 100 items. Some of the alternatives we can choose: – 0 for player 1 and 100 for player 2 (total value of 0+30=30) – 25 for player 1 and 75 for player 2 (total value of 10+22=32) – 75 for player 1 and 25 for player 2 (total value of 23+0=23) • We cannot choose 64 for player 1 and 36 for player 2 (total value of 23+20=43). • We choose 25 for player 1 and 75 for player 2 (total value 32).

Properties Claim: We can find the optimal allocation (among all possible allocations) with order of n 5 operations. Proof: with dynamic programming, very similar to before.

Properties Claim: We can find the optimal allocation (among all possible allocations) with order of n 5 operations. Proof: with dynamic programming, very similar to before. Claim: The obtained allocation, a, has total welfare at least half of the optimal welfare, o (i. e. Σj vj(o) < 2 Σj vj(a) ).

Properties Claim: We can find the optimal allocation (among all possible allocations) with order of n 5 operations. Proof: with dynamic programming, very similar to before. Claim: The obtained allocation, a, has total welfare at least half of the optimal welfare, o (i. e. Σj vj(o) < 2 Σj vj(a) ). Proof: Let i be a player with oi > M/n. Case 1: vi(oi) > Σj≠i vj(oj). Then Σj vj(o) < 2 vi(M) < 2 Σj vj(a).

Properties Claim: We can find the optimal allocation (among all possible allocations) with order of n 5 operations. Proof: with dynamic programming, very similar to before. Claim: The obtained allocation, a, has total welfare at least half of the optimal welfare, o (i. e. Σj vj(o) < 2 Σj vj(a) ). Proof: Let i be a player with oi > M/n. Case 1: vi(oi) > Σj≠i vj(oj). Then Σj vj(o) < 2 vi(M) < 2 Σj vj(a). Case 2: vi(oi) < Σj≠i vj(oj). Consider the allocation d in which player i gets nothing and every j ≠ i gets oj rounded up to the next multiple of b. We added at most nb items and removed at least M/n items, and so, since nb < M/n, the allocation d is valid. We get: Σj vj(o) < 2 Σj≠i vj(oj) < 2 Σj vj(d) < 2 Σj vj(a).

Conclusion • There exists a computationally-efficient truthful multi-unit auction that always obtains at least half of the optimal welfare. • Main open question: what about the revenue? – (Nothing is currently known about the revenue!)