QUADRATIC EQUATIONS QUADRATIC EQUATIONS CONCEPT OF COMMON ROOTS

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS CONCEPT OF COMMON ROOTS

QUADRATIC EQUATIONS Proof Necessity Let be a common root of the given equations then

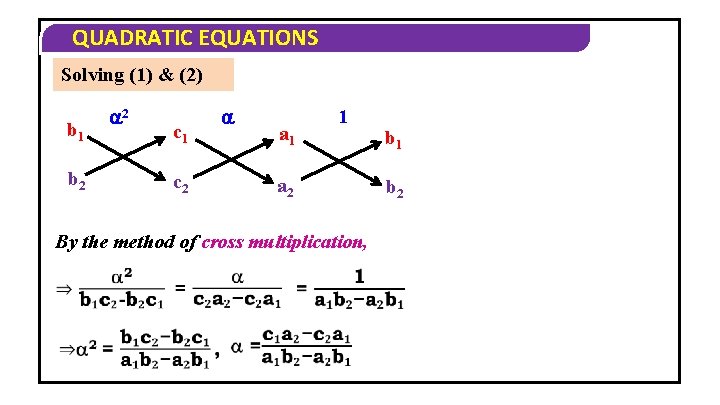
QUADRATIC EQUATIONS Solving (1) & (2) b 1 b 2 2 c 1 c 2 a 1 1 a 2 By the method of cross multiplication, b 1 b 2

QUADRATIC EQUATIONS Sufficiency Suppose that Case (i) a 1 b 2 – a 2 b 1=0 then c 1 a 2 -c 2 a 1=0 (from 5)

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS Case (ii)

QUADRATIC EQUATIONS =0 i. e. , a 1 2+b 1 +c 1=0 similarly we can prove that a 2 2+b 2 +c 2=0. Thus, ‘ ’ is a common root of the given equations

QUADRATIC EQUATIONS 1) If x 2+4 ax+3=0 and 2 x 2+3 ax-9=0 have a common root, then find the values of ‘a’ and the common roots. Solution a =1, b 1=4 a, c 1=3, Here 1 a 2=2, b 2=3 a, c 2=-9 are substitute in the condition

QUADRATIC EQUATIONS i. e. , 225 = (-5 a)(-45 a) i. e. , a 2=1 So, a= 1 If a=-1, the common root = 3, If a=1, the common root = -3

QUADRATIC EQUATIONS APPLICATIONS RELATED TO Q. E.

QUADRATIC EQUATIONS REDUCIBLE TO QUADRATIC EQUATIONS Here is an explanation with some illustrations how to solve some equations which are reducible to quadratic equations by suitable substitutions.

QUADRATIC EQUATIONS 1) Solve 71+x+71 -x-50 = 0 Solution By factorization On taking 7 x=t, this equation becomes 7 t 2 -50 t+7=0 i. e. , (7 t-1) (t-7) = 0

QUADRATIC EQUATIONS Bases are equal. On equating the powers we get x = -1 or x = 1 The solution set of the given equation is {-1, 1}

QUADRATIC EQUATIONS Solution By factorization 2 t 2 -5 t+2=0 2 t 2 -4 t-t+2=0

QUADRATIC EQUATIONS 4 x = x-3 (or) x = 4 x-12 x = -1 (or) x = 4 It can be verified that x=-1 and x=4 satisfies the given equation The solution set of the given equation is {-1, 4}

QUADRATIC EQUATIONS Solution 2 t 2 -7 t+5=0 (2 t-5)(t-1)=0 By factorization

QUADRATIC EQUATIONS 2 x 2 -5 x+2=0 (or) x 2 -x+1=0 ∵ i 2=-1

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 4) Solve 2 x 4+x 3 -11 x 2+x+2=0 Solution Since x=0 is not a solution of the given equation On dividing the given equation by x 2, we get

QUADRATIC EQUATIONS 2(y 2 -2)+y-11 = 0 2 y 2+y-15=0 (2 y-5)(y+3)=0

QUADRATIC EQUATIONS 2 x 2 -5 x+2=0 (or) x 2+3 x+1=0

QUADRATIC EQUATIONS 5) Prove that there is a unique pair of consecutive odd positive integers such that the sum of their squares is 290 and find it. Solution Since two consecutive odd integers differ by 2, we have to prove that there is unique positive odd integer x, such that x 2+(x+2)2=290 (1) 2 x 2+4 x-286=0 x 2+2 x-143=0

QUADRATIC EQUATIONS x 2+13 x-11 x-143 = 0 (x+13)(x-11) = 0 x = -13 (or) � x=11 Given that the number is odd positive integer. � Hence ‘ 11’ is the only positive odd integer satisfying equation (1) Now (x, x+2) = (11, 13) is the unique pair of integers which satisfies the given condition

QUADRATIC EQUATIONS 6) Find the number which exceeds its positive square root by 12 Solution Let ‘x’ be any such number Squaring on both sides, we get (x-12)2 = x x 2 -24 x+144 = x

QUADRATIC EQUATIONS x 2 -25 x+144 = 0 (x-16)(x-9) = 0 x = 16 and x = 9 are roots of above equation But x=9 does not satisfy the equation (1) while x=16 satisfies (1) Required number is 16.

QUADRATIC EQUATIONS 7) The cost of a piece of cable wire is Rs. 35/-. If the length of the piece of wire is 4 meters more each meter costs Rs. 1/- less, the cost would remain unchanged. Find the length of the wire. Solution Let the length of the piece of wire be ‘l ’ meters and the cost of each meter be Rs. x/-, then l. x=35 (1)

QUADRATIC EQUATIONS Given the length of the piece of wire is 4 meters more each meter costs Rs. 1/- less (l+4)(x-1) = 35 lx-l+4 x-4 = 35 35 -l+4 x-4 = 35 4 x=l+4 From eq(1) lx = 35

QUADRATIC EQUATIONS Substitute ‘x’ in (1), we get l 2+4 l-140=0 (l+14)(l-10)=0 l = -14 (or) l =10 Since the length cannot be negative, l =10 meters

QUADRATIC EQUATIONS 8) If x 1, x 2 are the roots of ax 2+bx+c=0 then find the value of (ax 1+b)2+(ax +b)-2 2 Solution x 1 is the root of ax 2+bx+c=0 x 1(ax 1+b) = -c ax 12+bx 1+c=0

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 9(i) If , are the roots of ax 2+bx+c=0 find the quadratic equation whose roots are p , p Solution p pβ

QUADRATIC EQUATIONS The equation whose roots are P and P is x 2 -(P +P )x+(P ) = 0

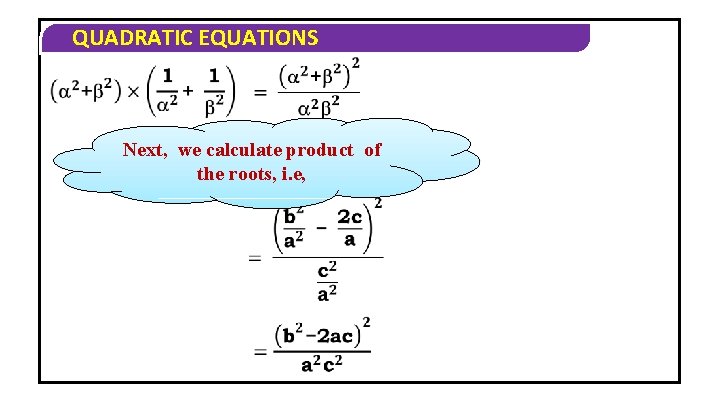
QUADRATIC EQUATIONS 9(ii) If , are the roots of ax 2+bx+c=0 find the quadratic equation whose roots are 2+ 2, -2+ -2 Solution Firstly we calculate sum of the roots, i. e,

QUADRATIC EQUATIONS Next, we calculate product of the roots, i. e,

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 10) Find the quadratic equation for which the sum of the roots is 1 and the sum of the squares of the roots is 13. Solution Let and be the roots of the required equation, then + =1 2+ 2 =13 = -6

QUADRATIC EQUATIONS Required equation =

QUADRATIC EQUATIONS 11) Find the condition that one root of ax 2+bx+c=0 may be n times the other root. Solution Let and n be the roots of given equation, then Substituting (1) in (2) we get

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 12) If the equation x 2+ax+b=0 and x 2+cx+d=0 have a common root and the first equation has equal roots then prove that 2(b+d)=ac Solution Let be a common root of x 2+ax+b=0 and x 2+cx+d=0 then 2+a +b=0 (1) 2+c +d=0 (2) But first equation has equal roots

QUADRATIC EQUATIONS Then + = -a 2+c +d=0 (2) from eq (2) 2 (b+d) = ac

QUADRATIC EQUATIONS Thank you…