PT symmetry and supersymmetry June 23 2004 XI




















































![Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> = Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> =](https://slidetodoc.com/presentation_image/e49f5286f1b9cb5b3238c462cde0c883/image-53.jpg)
![Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> = Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> =](https://slidetodoc.com/presentation_image/e49f5286f1b9cb5b3238c462cde0c883/image-54.jpg)








- Slides: 62

PT symmetry and supersymmetry June 23, 2004 XI SYMPHYS, Prague

PT symmetry and supersymmetry Parallels between the concepts of symmetry, supersymmetry and (recently introduced) PT symmetry June 23, 2004 XI SYMPHYS, Prague

PT symmetry and supersymmetry Parallels between the concepts of symmetry, supersymmetry and (recently introduced) PT symmetry reviewed and discussed by M. Znojil [XI SYMPHYS, Prague, June 21 – 24, 2004] June 23, 2004 XI SYMPHYS, Prague

Collaborations: • B. Bagchi (India) • E. Caliceti (Italy) • F. Cannata (Italy) • F. Gemperle (Czechia) • V. Gerdt (Russia) • V. Jakubsky (Czechia) • G. Levai (Hungary) • O. Mustafa (Turkey) • C. Quesne (Belgium) • P. Roy (India) • R. Roychoudhury (India) • M. Tater (Czechia) • A. Ventura (Italy) • D. Yanovich (Russia) June 23, 2004 XI SYMPHYS, Prague

Also referring to the talks by: • F. Ardalan • N. Belaloui • J. M. Cervero • F. Gieres • P. Mathieu • A. Mostafazadeh • A. Nikitin • G. Pogosyan • F. Toppan June 23, 2004 XI SYMPHYS, Prague

TABLE OF CONTENTS I. ZOO OF SYMMETRIES II. ZOO ANIMALS IN PAIRS III. SUSY PLUS PT-SYMMETRY IV. RELATIVISTIC KINEMATICS V. CONCLUSIONS June 23, 2004 XI SYMPHYS, Prague

I. The concept of symmetries (A) ORIGINS: LIE ALGEBRAS: bound – states: subspace with a symmetry, P |y(z)> = z |y(z)> + Schroedigner equation, H |y(z)> = E(z) |y(z)> = vanishing commutator: H P = P H for illustration: parity P admissible z = +1 or -1 doubly-indexed spectrum: June 23, 2004 XI SYMPHYS, Prague n = 0, 1, . . .

I. The concept of symmetries (A) ORIGINS: LIE ALGEBRAS: bound – states: subspace with a symmetry, P |y(z)> = z |y(z)> + Schroedigner equation, H |y(z)> = E(z) |y(z)> = vanishing commutator: H P = P H for illustration: parity P admissible z = +1 or -1 doubly-indexed spectrum: June 23, 2004 XI SYMPHYS, Prague n = 0, 1, . . .

Symmetries APPLICATIONS ctd: beyond parity: crystallographic studies and the like, H = atomic, nuclear, . . . physics z = angular momenta etc y = field theory, particle physics etc: symmetries = Lie groups June 23, 2004 XI SYMPHYS, Prague

Symmetries (B) AN ALTERNATIVE IDEA: SUPERSYMMETRY: cf. the graded Lie algebra sl(1|1): three ‘graded’ generators: H plus Q and P ‘fermionic’ PP=QQ=0, plus a new compatibility: H P - P H = H Q - Q H = 0 while P Q + Q P = H June 23, 2004 XI SYMPHYS, Prague

Symmetries SUPERSYMMETRY and sl(1|1) ctd. specific representation of operators: SUSY QM: H = direct sum of the ‘left’ and ‘right’ H(L, R) Q (lower, a) and P (upper, c) are nilpotent, D=2 a = upper (annih. ), c = lower (creation), D=oo related representation of |y(z)>: two components in |y(z)>: z=(f, b), f = 0 or 1 conventional HO: f=1 if |b> = down, f=0 if up June 23, 2004 XI SYMPHYS, Prague

Symmetries SUPERSYMMETRY and sl(1|1) ctd. specific representation of operators: SUSY QM: H = direct sum of the ‘left’ and ‘right’ H(L, R) Q (lower, a) and P (upper, c) are nilpotent, D=2 a = upper (annih. ), c = lower (creation), D=oo related representation of |y(z)>: two components in |y(z)>: z=(f, b), f = 0 or 1 conventional HO: f=1 if |b> = down, f=0 if up June 23, 2004 XI SYMPHYS, Prague

Symmetries SUPERSYMMETRY, sl(1|1), 2 x 2 operators and 2 -D |y(f, b)> ctd. • solvable HO, field theory (Fock space): • non-vanishing Q |y(0, b)> = z |y(1, b-1)> non-vanishing • P |y(1, b)> = z’ |y(0, b+1)> applications beyond HO: two Schroedigner equations and a partnership E(L, R) partners H -> shape invariance, exact solvability June 23, 2004 XI SYMPHYS, Prague

Symmetries SUPERSYMMETRY, sl(1|1), 2 x 2 operators and 2 -D |y(f, b)> ctd. • solvable HO, field theory (Fock space): • non-vanishing Q |y(0, b)> = z |y(1, b-1)> non-vanishing • P |y(1, b)> = z’ |y(0, b+1)> applications beyond HO: two Schroedigner equations and a partnership E(L, R) partners H -> shape invariance, exact solvability June 23, 2004 XI SYMPHYS, Prague

Symmetries (C) Introduction of the third class of antilinear, so called PT - SYMMETRIES • a prelude: a return to time-reversal T-symmetry review QM note that T-operation coincides with h. c. -operation • pre-history: BW (‘ 68): natural complexification of perturbations CGM (‘ 80): real energies for imaginary cubic AHO B (‘ 92): numerical experiments with V(x) = i x^3 BG (‘ 93): real spectra at quartic repulsion V=-x^4 June 23, 2004 XI SYMPHYS, Prague

Symmetries (C) Introduction of the third class of antilinear, so called PT - SYMMETRIES • a prelude: a return to time-reversal T-symmetry review QM note that T-operation coincides with h. c. -operation • pre-history: BW (‘ 68): natural complexification of perturbations CGM (‘ 80): real energies for imaginary cubic AHO B (‘ 92): numerical experiments with V(x) = i x^3 BG (‘ 93): real spectra at quartic repulsion V=-x^4 June 23, 2004 XI SYMPHYS, Prague

Symmetries, use of PT symmetry: NON-HERMITIAN QUANTUM THEORIES: • idea: Hermiticity violated in pert. theory, in phenomenology (condensed matter, biology) etc. • the first implementations of PT symmetry: BM (‘ 97): delta-expansions (in field theory) BB (‘ 98): WKB (in quantum mechanics) CJT (‘ 98): exact (Bessel functions) FGRZ (‘ 98): perturbations (of imaginary cubic) BB (‘ 98): QES quartic June 23, 2004 XI SYMPHYS, Prague

Symmetries A RETURN TO CLASSICS: • representations: Wigner in 1960’s (+rediscoveries) • fights for an acceptance in physics: indefinite metric in 1940’s (Dirac etc) Gupta and Bleuler and their elimination trick relativistic QM and 2 x 2 KG equation: FV (‘ 58) field-models of Lie, Wick and Nishijima MHD: U. G. , cosmology: A. M. exceptional points (BW singularities, measured !) June 23, 2004 XI SYMPHYS, Prague

Symmetries PT - SYMMETRY’s SUMMARY: • an agreement on its consistency in physics: quasi-parity: Z (‘ 99), BQZ (‘ 01) the existence of the metric eta plus: M (‘ 02) CPT symmetric formulation: BBJ (‘ 02) • a steady development of mathematics: proofs [DDT (‘ 02), S (‘ 03)] quasi-Hermiticity [SGH (‘ 92) + re-discoveries] systematics and classifications: ES, QES. . . manybody, multidimensional (Calogero, Henon-Heiles) June 23, 2004 XI SYMPHYS, Prague

Symmetries PT - SYMMETRY’s SUMMARY: • an agreement on its consistency in physics: quasi-parity: Z (‘ 99), BQZ (‘ 01) the existence of the metric eta plus: M (‘ 02) CPT symmetric formulation: BBJ (‘ 02) • a steady development of mathematics: proofs [DDT (‘ 02), S (‘ 03)] quasi-Hermiticity [SGH (‘ 92) + re-discoveries] systematics and classifications: ES, QES. . . manybody, multidimensional (Calogero, Henon-Heiles) June 23, 2004 XI SYMPHYS, Prague

June 23, 2004 XI SYMPHYS, Prague

June 23, 2004 XI SYMPHYS, Prague

II. An interplay of symmetries (an exhaustive list of the three possibilities) - 1 (A-B) interface between LIE and SUPER - SYMMETRY will be skipped here: just a few remarks: • typical for field theory: multiplets, standard model • absence of SUSY partners in experiments • methodical laboratory: Witten’s SUSY QM June 23, 2004 XI SYMPHYS, Prague

An interplay of symmetries (a systematic review) - 2 (A-C) interface between LIE and PT - SYMMETRY will be skipped here: just a few remarks: • typical for solvable models: sl(2, 2) [BQ (‘ 92)] • new models, new Hermitian limits [ZT (‘ 91)] • methodical innovations: new boundary conditions • an efficient regularization of singularities June 23, 2004 XI SYMPHYS, Prague

An interplay of symmetries (a systematic review) - 3 (B-C) interface between SUSY and PT - SYMMETRY a core of our message - key points: • new classes of representations • efficient regularization recipes • explicit constructions • new models June 23, 2004 XI SYMPHYS, Prague

III. Interplay between PT and SUSY Harmonic oscillators are, after PT symmetrization, numbered by (non-integer) parameter g or a = |g|: = 1/2 in Hermitian case sign-parameter q (= +1 or -1) added q = -1 (fixed) in Hermitian case • energies E = 4 n+2 -2 a q Laguerre-polynomial wavefunctions exceptional points = unavoided level crossings • June 23, 2004 XI SYMPHYS, Prague

PT and SUSY representations: SUSY HO example: • initial superpotential W(g) • partners: H(L)= H(a)-2 g-2, • H(R)= H(b)-2 g, a = |g|, b = |g+1|, • hierarchy E (+, a) < E (+, b) < E (-, a) < E (-, b), ground E(L)=min(0, -4 g) (right: deg. and neg. ) the first excited R-state: E=min(4, -4 g) the 2 nd excited: max(0, -4 g) (right: nedeg. 0) June 23, 2004 XI SYMPHYS, Prague

PT and SUSY representations: SUSY HO example: • initial superpotential W(g) • partners: H(L)= H(a)-2 g-2, • H(R)= H(b)-2 g, a = |g|, b = |g+1|, • hierarchy E (+, a) < E (+, b) < E (-, a) < E (-, b), ground E(L)=min(0, -4 g) (right: deg. and neg. ) the first excited R-state: E=min(4, -4 g) the 2 nd excited: max(0, -4 g) (right: nedeg. 0) June 23, 2004 XI SYMPHYS, Prague

PT and SUSY - representations SUSY action: A(g) |y(g, n+1)> = c |y(g+1, n)> A(g) |y(-g, n)> = d(g) |y(-g-1, n)> C(g) |y(g+1, n)> = c |y(g, n+1)> C(g) |y(-g-1, n)> = d(g) |y(-g, n)> June 23, 2004 XI SYMPHYS, Prague

PT and SUSY regularizations: • SUSY failure Jevicki-Rodrigues g=1/2 paradox: E(L)=(-2, 0, 2, 4, …) E(R)=(4, 8, 12, …) • Das-Pernice resolution: delta-function in the origin and shift +2 • PT analytic resolution: E(R)=(-2, 2, 4, 6, …) June 23, 2004 XI SYMPHYS, Prague

PT and SUSY regularizations: • SUSY failure Jevicki-Rodrigues g=1/2 paradox: E(L)=(-2, 0, 2, 4, …) E(R)=(4, 8, 12, …) • Das-Pernice resolution: delta-function in the origin and shift +2 • PT analytic resolution: E(R)=(-2, 2, 4, 6, …) June 23, 2004 XI SYMPHYS, Prague

PT and SUSY regularizations: • SUSY failure Jevicki-Rodrigues g=1/2 paradox: E(L)=(-2, 0, 2, 4, …) E(R)=(4, 8, 12, …) • Das-Pernice resolution: delta-function in the origin and shift +2 • PT analytic resolution: E(R)=(-2, 2, 4, 6, …) June 23, 2004 XI SYMPHYS, Prague

PT and SUSY interpretations • singular HO in a new picture: 1. define the second-order operators: A(g -1) x A(-g) = A(a) C(g) x C(-g -1) = C(a) 2. derive q-dependent creation/annihilation: A(a) |y(g, n+1)> = f(g) |y(g, n)> C(a) |y(g, n)> = f(g) |y(g, n+1)> June 23, 2004 XI SYMPHYS, Prague

PT and SUSY interpretations • singular HO in a new picture: 1. define the second-order operators: A(g -1) x A(-g) = A(a) C(g) x C(-g -1) = C(a) 2. derive q-dependent creation/annihilation: A(a) |y(g, n+1)> = f(g) |y(g, n)> C(a) |y(g, n)> = f(g) |y(g, n+1)> June 23, 2004 XI SYMPHYS, Prague

PT and SUSY SSUSY representation: 4. close the Lie algebra sl(2, R): 8 H(a) = A(a) C(a) - C(a) A(a) 4 A(a) = A(a) H(a) - H(a) A(a) 4 C(a) = H(a) C(a) - C(a) H(a) 5. get the new H(L) = [H(a) - 2]^2 - 4 a^2 and the new H(R) = [H(a) + 2]^2 - 4 a^2 June 23, 2004 XI SYMPHYS, Prague

PT and SUSY SSUSY representation: 4. close the Lie algebra sl(2, R): 8 H(a) = A(a) C(a) - C(a) A(a) 4 A(a) = A(a) H(a) - H(a) A(a) 4 C(a) = H(a) C(a) - C(a) H(a) 5. get the new H(L) = [H(a) - 2]^2 - 4 a^2 and the new H(R) = [H(a) + 2]^2 - 4 a^2 June 23, 2004 XI SYMPHYS, Prague

PT and SUSY plans for the nearest future: 6. weaken PT symmetry to CPT symmetry P -> P(gen) = C P, (PT broken: KM ‘ 91 etc) C -> any differential operator (A ‘ 92, KS ‘ 04) re-install SUSY (CCZV ‘ 04) June 23, 2004 XI SYMPHYS, Prague

IV. Prominent application: Klein-Gordon field HAMILTONIANS? FESHBACH - VILLARS! (two-by-two matrices - cf. Mostafazadeh on Monday) June 23, 2004 XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS HAMILTONIANS (two-by-two matrices) POTENTIALS? SIMPLE MODELS m=m(x, E) (exactly solvable examples) interpretation: transitions to lower energies (energy-dependence!) meaning: non-Hermitian D admitted June 23, 2004 XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS SCALAR POTENTIALS m=m(x, E) equation: -y‘‘=Dy and abbreviations iy‘=u, y=v re-written iu‘=Dv, iv‘=u, i. e. , two-dimensional i Y‘=H Y or | u‘ | i | | = | v‘ | June 23, 2004 |0 D| |u| | |I 0| |v| XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS SCALAR POTENTIALS m=m(x, E) SURPRIZE: PT-SYMMETRY!. i. e. , two-dimensional PT-symmetry rule s. T H = H s. T where the ‘metric‘ is anti-Hermitian, s = June 23, 2004 | 0 I| | -I 0 | XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS PT-SYMMETRY. energy-representation | u| |0 D| |u| E | | = | | | v| |I 0| |v| and solution (Dv=Eu, u = Ev, Du = E^2 u): | u| | | = | v| June 23, 2004 |Eu| | E | | | = | |. u | | 1 | XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS PT-SYMMETRY. D-spectrum positive (Du = E^2 u), H-spectrum in the positive/negative pairs, with remarkable wavefunctions, | Eu| | | , | u | June 23, 2004 | -Eu| | u | XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS NEW REQUIREMENT - SUPERSYMMETRY, formed by L + R direct sum: G= | H(L) 0 | | | = PQ+QP | 0 H(R) | where | 0 0 | Q= | |, | A 0 | June 23, 2004 | 0 C | P = | | | 0 0 | XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS CONSEQUENCES OF PT-SUPERSYMMETRY. submatrices A and C are two-by-two: | a 0 | A= | |, | 0 b | | 0 g | C = | | | d 0 | SUSY requires that g b = D(L), a g = D(R), and d a = I , b d = I. June 23, 2004 XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS PT-SUPERSYMMETRY. the first two rules = non-relativistic SUSY: g b = D(L), a g = D(R), i. e. , annihilation and creation, respectively: | a 0 | AC = | | | 0 b | x | 0 g | | d 0 | the latter two conditions must be weakened, d a = I , b d = P = I - |0> <0| June 23, 2004 XI SYMPHYS, Prague

Klein Gordon FESHBACH - VILLARS PT-SUPERSYMMETRY. the first two rules = non-relativistic SUSY: g b = D(L), a g = D(R), i. e. , annihilation and creation, respectively: | a 0 | AC = | | | 0 b | x | 0 g | | d 0 | the latter two conditions must be weakened, d a = I , b d = P = I - |0> <0| June 23, 2004 XI SYMPHYS, Prague

Klein Gordon PT-SUPERSYMMETRY. We may emphasize: there are three levels of Hilbert spaces: 1. D=1 level of action of D(L) and D(R), plus their 2 -component direct sum: 2. D=2 level of action of H(L) and H(R), plus their 4 -component direct sum: 3. D=4 SUSY level of the action of G , on all of them we have kets |u(D)> i. e. , 1. right eigenstates u = |u(1)> of D, 2. FV 2 -component right eigenstates of H 3. SUSY 4 -component right eigenstates of G and PT, non-conjugate bras June 23, 2004 XI SYMPHYS, Prague <<u(D)|.

Klein Gordon PT-SUPERSYMMETRY. We may emphasize: there are three levels of Hilbert spaces: 1. D=1 level of action of D(L) and D(R), plus their 2 -component direct sum: 2. D=2 level of action of H(L) and H(R), plus their 4 -component direct sum: 3. D=4 SUSY level of the action of G , on all of them we have kets |u(D)> i. e. , 1. right eigenstates u = |u(1)> of D, 2. FV 2 -component right eigenstates of H 3. SUSY 4 -component right eigenstates of G and PT, non-conjugate bras June 23, 2004 XI SYMPHYS, Prague <<u(D)|.

Klein Gordon PT-SUPERSYMMETRY. We may emphasize: there are three levels of Hilbert spaces: 1. D=1 level of action of D(L) and D(R), plus their 2 -component direct sum: 2. D=2 level of action of H(L) and H(R), plus their 4 -component direct sum: 3. D=4 SUSY level of the action of G , on all of them we have kets |u(D)> i. e. , 1. right eigenstates u = |u(1)> of D, 2. FV 2 -component right eigenstates of H 3. SUSY 4 -component right eigenstates of G and PT, non-conjugate bras June 23, 2004 XI SYMPHYS, Prague <<u(D)|.

Klein Gordon PT-SUPERSYMMETRY. In all these three cases, the action of G(D) may be both right and left: , G(D) |u(D)> = E(D) |u(D)> <<u(D)| G(D) = <<u(D)| . E(D) As long as h. c. (G) = h G 1/h , we may assume Im E = 0 and get quasi-parities, |u(D, m)>> = q(D, m). [h |u(D, m)>]. Insertions give relations between q(1, m), q(2, m) and q(3, m). June 23, 2004 XI SYMPHYS, Prague

Klein Gordon PT-SUPERSYMMETRY. In all these three cases, the action of G(D) may be both right and left: , G(D) |u(D)> = E(D) |u(D)> <<u(D)| G(D) = <<u(D)| . E(D) As long as h. c. (G) = h G 1/h , we may assume Im E = 0 and get quasi-parities, |u(D, m)>> = q(D, m). [h |u(D, m)>]. Insertions give relations between q(1, m), q(2, m) and q(3, m). June 23, 2004 XI SYMPHYS, Prague
![Klein Gordon PTSUPERSYMMETRY biorthogonality Em En uD m uD n Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> =](https://slidetodoc.com/presentation_image/e49f5286f1b9cb5b3238c462cde0c883/image-53.jpg)
Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> = 0, • overlaps << u(D, m)| u(D, n)> = 1/R(m) d(m, a), • completeness S | u(D, m)> 1/R(m) << u(D, m)| = 1 SE level (where E = positive) : D=1, m = 0, 1, . . . …, on the KG level (non-zero E): D=2, sign E = t = +1 and -1 on the SUSY level: D=4, L and R, bosons - fermions June 23, 2004 XI SYMPHYS, Prague
![Klein Gordon PTSUPERSYMMETRY biorthogonality Em En uD m uD n Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> =](https://slidetodoc.com/presentation_image/e49f5286f1b9cb5b3238c462cde0c883/image-54.jpg)
Klein Gordon PT-SUPERSYMMETRY. • bi-orthogonality [E(m) - E(n)] << u(D, m)| u(D, n)> = 0, • overlaps << u(D, m)| u(D, n)> = 1/R(m) d(m, a), • completeness S | u(D, m)> 1/R(m) << u(D, m)| = 1 SE level (where E = positive) : D=1, m = 0, 1, . . . …, on the KG level (non-zero E): D=2, sign E = t = +1 and -1 on the SUSY level: D=4, L and R, bosons - fermions June 23, 2004 XI SYMPHYS, Prague

Klein Gordon PT-SUPERSYMMETRY IN MARTRIX FORM: . sl(1|1) generated by three 4 x 4 items: 1. KG-super-Hamiltonian | | | G = | | June 23, 2004 0 D(L) 0 P 0 0 0 | | 0 D(R) | | I 0 | XI SYMPHYS, Prague

Klein Gordon PT-SUPERSYMMETRY MATRICES: . 2. KG-boson-annihilation supercharge | | | Q = | | June 23, 2004 0 0 0 0 a 0 0 b 0 0 XI SYMPHYS, Prague | | | |

Klein Gordon PT-SUPERSYMMETRY MATRICES: . 3. its boson-creation partner | | | P = | | June 23, 2004 0 0 0 g 0 0 d 0 0 0 0 0 XI SYMPHYS, Prague | | | |

Klein Gordon PT-SUPERSYMMETRY SUMMARY: There exists a remarkable physical interpretation of the exceptional E=0 ground-state. Due to our transition to relativistic kinematics, it becomes unstable against decay! OPEN QUESTION: DOES THIS EXPLAIN THE EXPERIMENTALLY OBSERVED ABSENCE OF SUSY PARTNERS IN PARTICLE PHYSICS? June 23, 2004 XI SYMPHYS, Prague

V. Summary • new ideas in SUSY: natural -> auxiliary metric P in Hilbert space Jordan blocks -> unavoided crossings of levels quasi-parity -> C PT symmetry -> probability • PT models in physics: Winternitzian and Calogerian models anew: non-equivalent Hermitian limits new types of tunnelling parallels between pseudo- and Hermitian SUSY June 23, 2004 XI SYMPHYS, Prague

V. Summary • new ideas in SUSY: natural -> auxiliary metric P in Hilbert space Jordan blocks -> unavoided crossings of levels quasi-parity -> C PT symmetry -> probability • PT models in physics: Winternitzian and Calogerian models anew: non-equivalent Hermitian limits new types of tunnelling parallels between pseudo- and Hermitian SUSY June 23, 2004 XI SYMPHYS, Prague

V. Summary • new ideas in SUSY: natural -> auxiliary metric P in Hilbert space Jordan blocks -> unavoided crossings of levels quasi-parity -> C PT symmetry -> probability • PT models in physics: Winternitzian and Calogerian models anew: non-equivalent Hermitian limits new types of tunnelling parallels between pseudo- and Hermitian SUSY June 23, 2004 XI SYMPHYS, Prague

V. Summary • new ideas in SUSY: natural -> auxiliary metric P in Hilbert space Jordan blocks -> unavoided crossings of levels quasi-parity -> C PT symmetry -> probability • PT models in physics: Winternitzian and Calogerian models anew: non-equivalent Hermitian limits new types of tunnelling parallels between pseudo- and Hermitian SUSY June 23, 2004 XI SYMPHYS, Prague
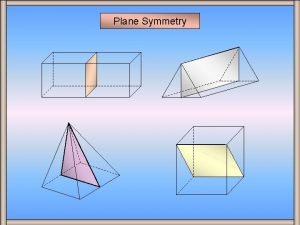
 Supersymmetry
Supersymmetry Supersymmetry
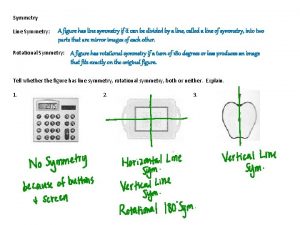
Supersymmetry Order of rotational symmetry
Order of rotational symmetry Symmetric in respect to the origin
Symmetric in respect to the origin 30 days has september april june and november
30 days has september april june and november March april may june july
March april may june july Guidance and counseling act of 2004
Guidance and counseling act of 2004 Spanish flacs exam 2018 answers
Spanish flacs exam 2018 answers June 2007 physics regents answers
June 2007 physics regents answers June 2005 calendar
June 2005 calendar Mitsl
Mitsl Good morning 1 june
Good morning 1 june What does lottery in june corn be heavy soon mean
What does lottery in june corn be heavy soon mean June 2010 chemistry regents
June 2010 chemistry regents Welcome june blessings
Welcome june blessings June 2021 english language paper 1
June 2021 english language paper 1 Life orientation grade 7 june exam
Life orientation grade 7 june exam Good morning welcome june
Good morning welcome june June 21 2019 geometry regents answers
June 21 2019 geometry regents answers Flacs checkpoint b spanish exam june 2015 answers
Flacs checkpoint b spanish exam june 2015 answers Cxc results 2018
Cxc results 2018 Britney spears real name
Britney spears real name When was lenore hetrick born
When was lenore hetrick born June cheetah wegener
June cheetah wegener Foreshadowing in the lottery
Foreshadowing in the lottery June canavan foundation
June canavan foundation Definition of vocabulary
Definition of vocabulary 19.06.2008 nasa
19.06.2008 nasa January 2018 regents chemistry
January 2018 regents chemistry New irpwm june 2020
New irpwm june 2020 June 20 2008
June 20 2008 A german cartoon published in 1919
A german cartoon published in 1919 June's journey
June's journey Good morning please
Good morning please Flacs b exam
Flacs b exam Summary period: june 2021 poem
Summary period: june 2021 poem Battle of midway june 1942
Battle of midway june 1942 Book a common noun
Book a common noun Drink before june 2012
Drink before june 2012 June too soon july stand by
June too soon july stand by Vfpms
Vfpms Rizal hereditary influence
Rizal hereditary influence June 22 to july 22
June 22 to july 22 June 6th 1944
June 6th 1944 Workshop expectations
Workshop expectations 1215 king
1215 king June preschool newsletter
June preschool newsletter June 23
June 23 Dr june carroll
Dr june carroll Tsc timetable
Tsc timetable June safety tips
June safety tips June 23
June 23 January 2012 chemistry regents
January 2012 chemistry regents John 20 21 22
John 20 21 22 Holy june
Holy june Companies in june
Companies in june 1 june children's day
1 june children's day Head start of greater dallas
Head start of greater dallas Dr june james
Dr june james June holley
June holley Milton glaser biography
Milton glaser biography June ward
June ward 2019 june calendar
2019 june calendar