8 1 Ratio and Proportion Slide 1 ObjectivesAssignment

8. 1 Ratio and Proportion Slide #1

Objectives/Assignment o o Find and simplify the ratio of two numbers. Use proportions to solve real-life problems, such as computing the width of a painting. Slide #2

Computing Ratios o If a and b are two quantities that are measured in the same units, then the ratio of a to be is a/b. The ratio of a to be can also be written as a: b. Because a ratio is a quotient, its denominator cannot be zero. Ratios are usually expressed in simplified form. For instance, the ratio of 6: 8 is usually simplified to 3: 4. (You divided by 2) Slide #3

Ex. 1: Simplifying Ratios o a. Simplify the ratios: 12 cm b. 6 ft 4 cm 18 ft Slide #4 c. 9 in. 18 in.

Ex. 1: Simplifying Ratios o a. Simplify the ratios: 12 cm b. 6 ft 4 m 18 in Solution: To simplify the ratios with unlike units, convert to like units so that the units divide out. Then simplify the fraction, if possible. Slide #5

Ex. 1: Simplifying Ratios o a. Simplify the ratios: 12 cm 4 m 4∙ 100 cm 12 400 Slide #6 3 100

Ex. 1: Simplifying Ratios o Simplify the ratios: b. 6 ft 18 in 6 ft 6∙ 12 in 18 in. 72 in. 18 in. Slide #7 4 1 4

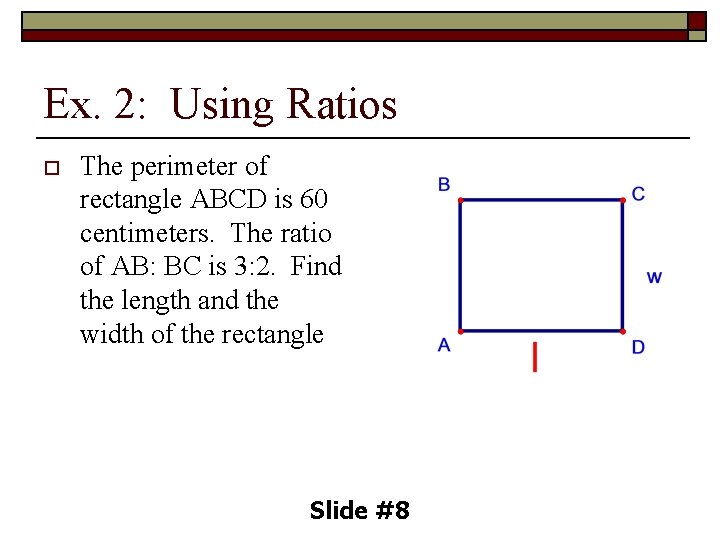
Ex. 2: Using Ratios o The perimeter of rectangle ABCD is 60 centimeters. The ratio of AB: BC is 3: 2. Find the length and the width of the rectangle Slide #8

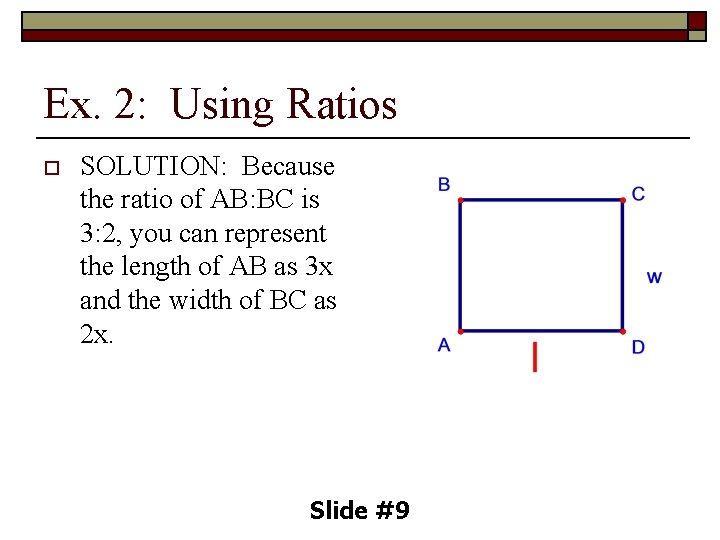
Ex. 2: Using Ratios o SOLUTION: Because the ratio of AB: BC is 3: 2, you can represent the length of AB as 3 x and the width of BC as 2 x. Slide #9

Solution: Statement 2 l + 2 w = P 2(3 x) + 2(2 x) = 60 6 x + 4 x = 60 10 x = 60 x=6 Reason Formula for perimeter of a rectangle Substitute l, w and P Multiply Combine like terms Divide each side by 10 So, ABCD has a length of 18 centimeters and a width of 12 cm. Slide #10

Ex. 3: Using Extended Ratios o o The measures of the angles in ∆JKL are in the extended ratio 1: 2: 3. Find the measures of the angles. Begin by sketching a triangle. Then use the extended ratio of 1: 2: 3 to label the measures of the angles as x°, 2 x°, and 3 x°. Slide #11 2 x° x° 3 x°

Solution: Statement x°+ 2 x°+ 3 x° = 180° 6 x = 180 x = 30 Reason Triangle Sum Theorem Combine like terms Divide each side by 6 So, the angle measures are 30°, 2(30°) = 60°, and 3(30°) = 90°. Slide #12

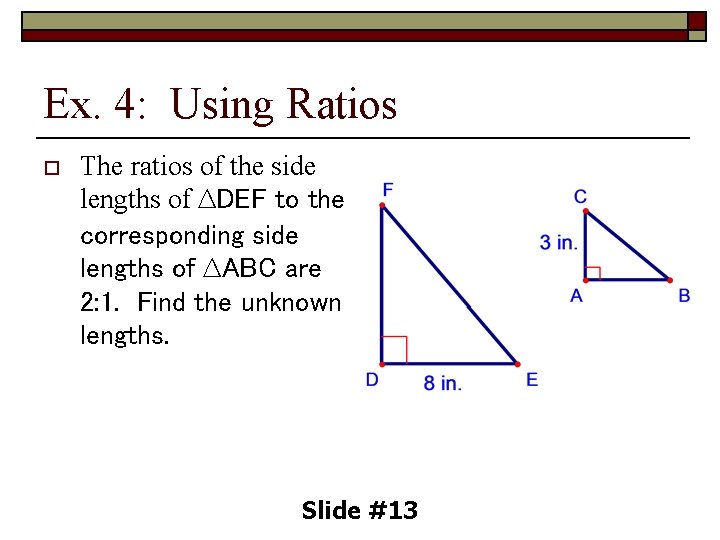
Ex. 4: Using Ratios o The ratios of the side lengths of ∆DEF to the corresponding side lengths of ∆ABC are 2: 1. Find the unknown lengths. Slide #13

Ex. 4: Using Ratios o SOLUTION: n n DE is twice AB and DE = 8, so AB = ½(8) = 4 Use the Pythagorean Theorem to determine what side BC is. DF is twice AC and AC = 3, so DF = 2(3) = 6 EF is twice BC and BC = 5, so EF = 2(5) or 10 4 in a 2 + b 2 = c 2 32 + 42 = c 2 9 + 16 = c 2 25 = c 2 5=c Slide #14

Using Proportions o An equation that equates two ratios is called a proportion. For instance, if the ratio of a/b is equal to the ratio c/d; then the following proportion can be written: Means Extremes = The numbers a and d are the extremes of the proportions. The numbers b and c are the means of the proportion. Slide #15

Properties of proportions 1. CROSS PRODUCT PROPERTY. The product of the extremes equals the product of the means. If = , then ad = bc Slide #16

Properties of proportions 2. RECIPROCAL PROPERTY. If two ratios are equal, then their reciprocals are also equal. = , then b = a To solve the proportion, you find the If value of the variable. Slide #17

Ex. 5: Solving Proportions 4 x 4 = Write the original proportion. 5 7 7 = 5 28 x = 5 4 Reciprocal prop. Multiply each side by 4 Simplify. Slide #18

Ex. 5: Solving Proportions 3 2 = y+2 y 3 y = 2(y+2) 3 y = 2 y+4 y = 4 Write the original proportion. Cross Product prop. Distributive Property Subtract 2 y from each side. Slide #19