Proof of the middle levels conjecture Torsten Mtze

Proof of the middle levels conjecture Torsten Mütze

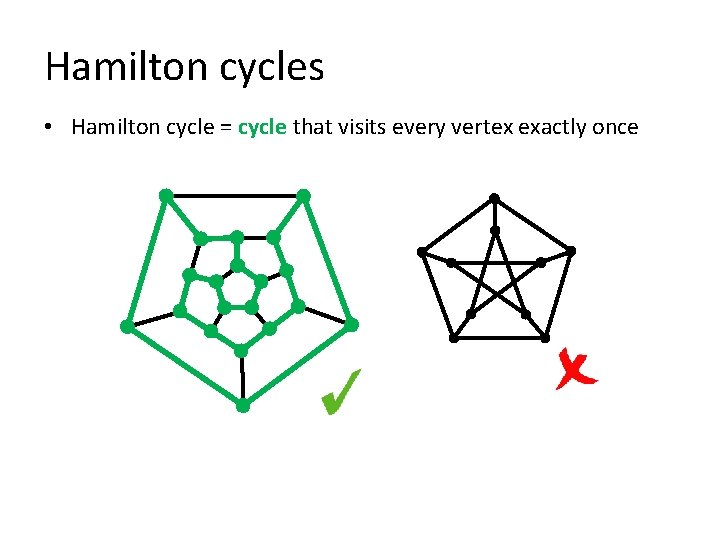
Hamilton cycles • Hamilton cycle = cycle that visits every vertex exactly once

Hamilton cycles • Problem: Given a graph, does it have a Hamilton cycle? • fundamental problem with many applications (special case of travelling salesman problem) • computational point of view: • no efficient algorithm known (NP-complete [Karp 72]), i. e. brute-force approach essentially best possible • what about particular families of graphs?

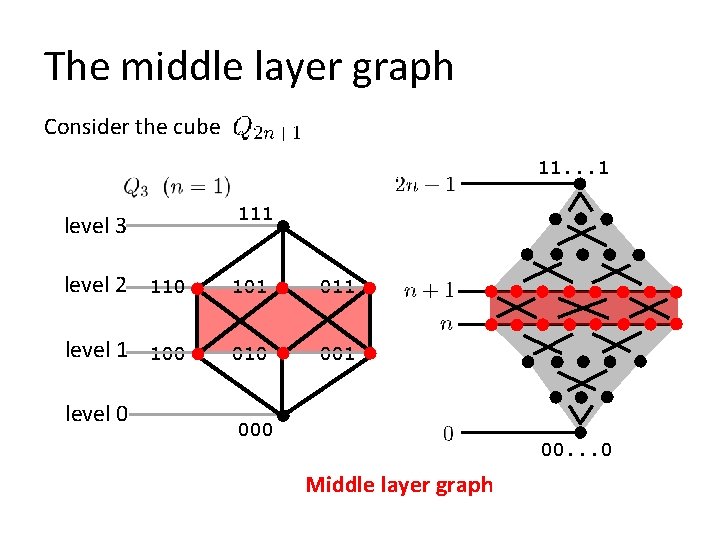
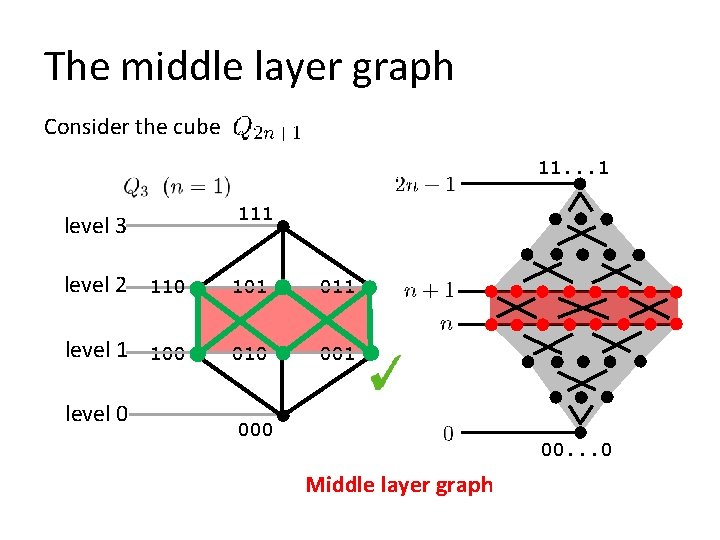
The middle layer graph Consider the cube 11. . . 1 level 3 111 level 2 110 101 011 level 1 100 010 001 level 0 00. . . 0 Middle layer graph

The middle layer graph Consider the cube 11. . . 1 level 3 111 level 2 110 101 011 level 1 100 010 001 level 0 00. . . 0 Middle layer graph

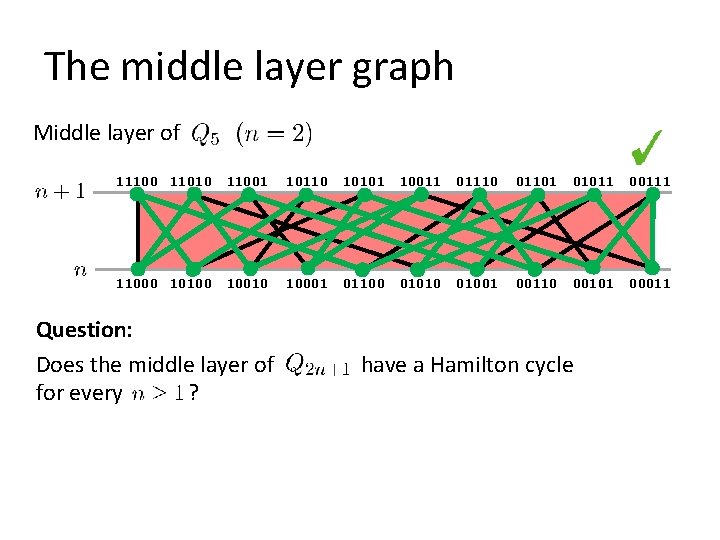
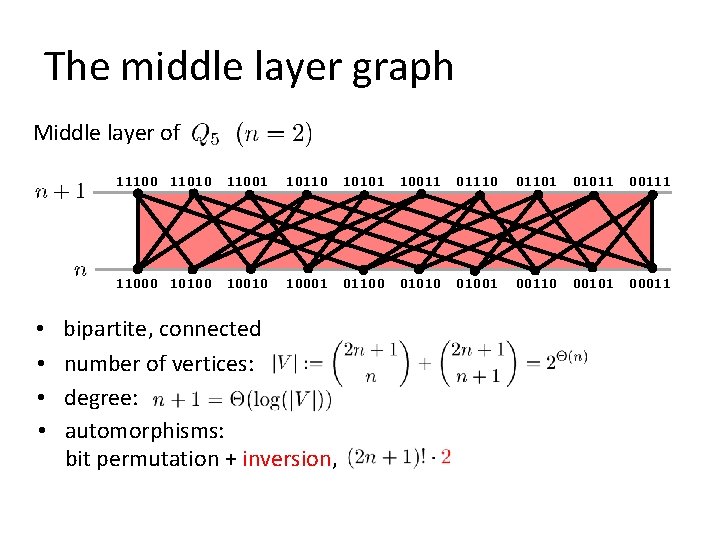
The middle layer graph Middle layer of 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 Question: Does the middle layer of for every ? have a Hamilton cycle

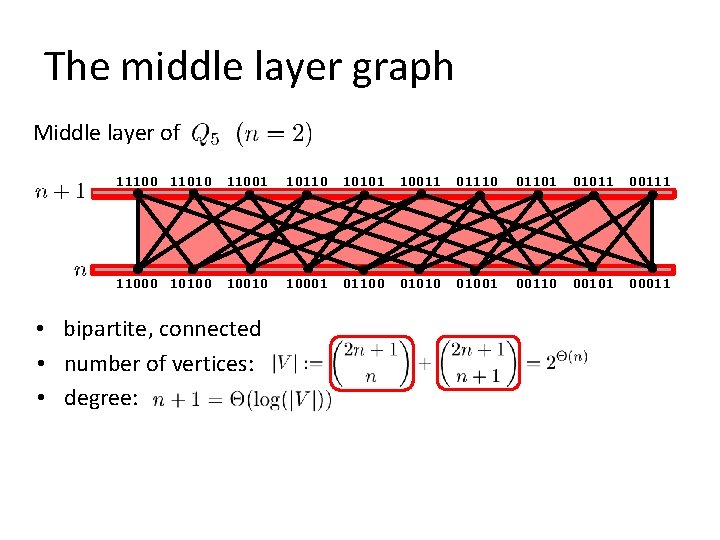
The middle layer graph Middle layer of 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 • bipartite, connected • number of vertices: • degree:

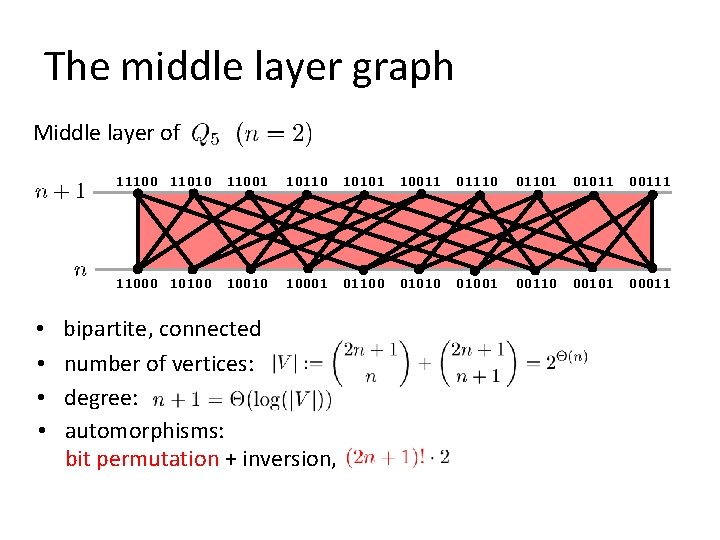
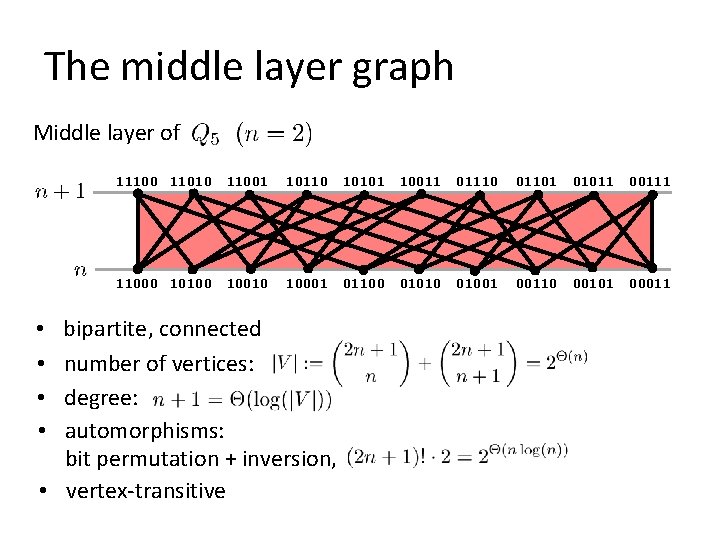
The middle layer graph Middle layer of • • 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 bipartite, connected number of vertices: degree: automorphisms: bit permutation + inversion,

The middle layer graph Middle layer of • • 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 bipartite, connected number of vertices: degree: automorphisms: bit permutation + inversion,

The middle layer graph Middle layer of 11100 11010 11001 10110 10101 10011 01110 01101 01011 00111 11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 bipartite, connected number of vertices: degree: automorphisms: bit permutation + inversion, • vertex-transitive • •

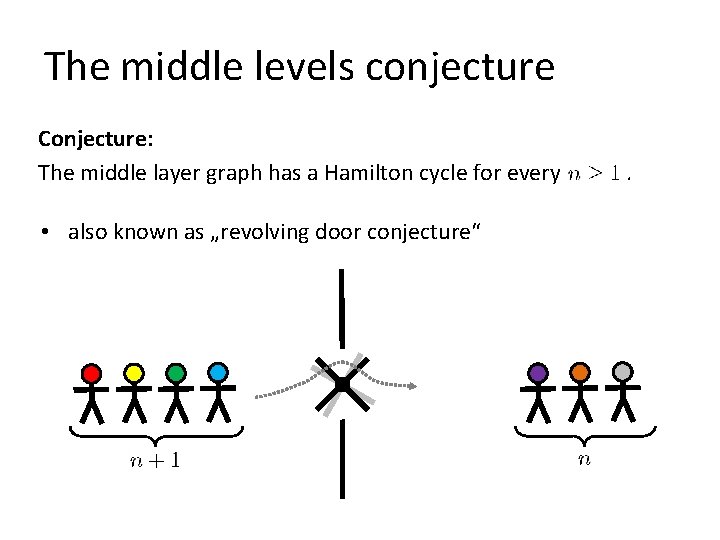
The middle levels conjecture Conjecture: The middle layer graph has a Hamilton cycle for every • also known as „revolving door conjecture“ .

The middle levels conjecture Conjecture: The middle layer graph has a Hamilton cycle for every . • probably first mentioned in [Havel 83], [Buck, Wiedemann 84] • also (mis)attributed to Dejter, Erdős, Trotter [Kierstead, Trotter 88] and various others • exercise (!!!) in [Knuth 05]

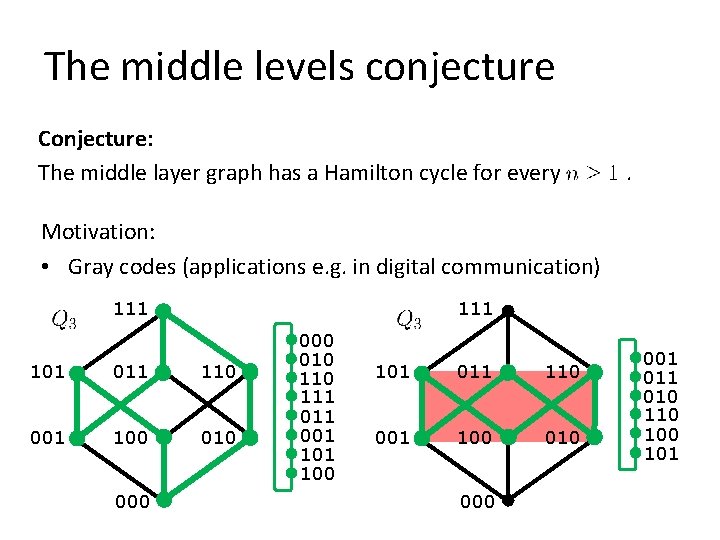
The middle levels conjecture Conjecture: The middle layer graph has a Hamilton cycle for every . Motivation: • Gray codes (applications e. g. in digital communication) 111 101 011 110 001 100 010 000 010 111 001 100 101 011 110 001 100 010 001 010 110 101

The middle levels conjecture Conjecture: The middle layer graph has a Hamilton cycle for every . Motivation: • Conjecture [Lovász 70]: Every connected vertex-transitive graph has a Hamilton cycle (apart from five exceptions).

History of the conjecture Numerical evidence: The conjecture holds for all [Moews, Reid 99], [Shields, Savage 09], [Shimada, Amano 11]

History of the conjecture Asymptotic results: The middle layer graph has a cycle of length • [Savage 93] • [Felsner, Trotter 95] • [Savage, Winkler 95] • [Johnson 04]

History of the conjecture Other relaxations and partial results: [Kierstead, Trotter 88] [Duffus, Sands, Woodrow 88] [Dejter, Cordova, Quintana 88] [Duffus, Kierstead, Snevily 94] [Hurlbert 94] [Horák, Kaiser, Rosenfeld, Ryjácek 05] [Gregor, Škrekovski 10] …

Our results Theorem 1: The middle layer graph has a Hamilton cycle for every Theorem 2: The middle layer graph has . different Hamilton cycles. Remarks: number of automorphisms is only , so Theorem 2 is not an immediate consequence of Theorem 1

Our results Theorem 1: The middle layer graph has a Hamilton cycle for every Theorem 2: The middle layer graph has . different Hamilton cycles. Remarks: number of Hamilton cycles is at most so Theorem 2 is best possible ,

Our results Theorem 1: The middle layer graph has a Hamilton cycle for every Theorem 2: The middle layer graph has . different Hamilton cycles. Remarks: proof is constructive algorithm to compute the cycle (inefficient) [M. , Nummenpalo 15+]: algorithm to compute next cycle vertex in time on average

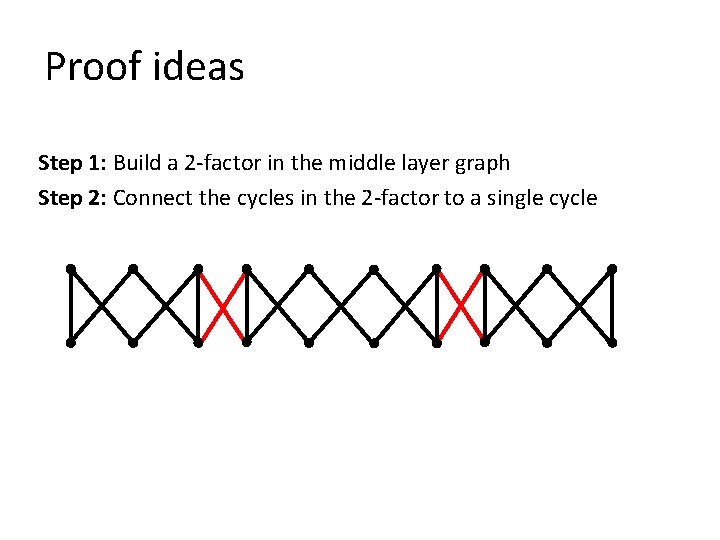
Proof ideas Step 1: Build a 2 -factor in the middle layer graph Step 2: Connect the cycles in the 2 -factor to a single cycle

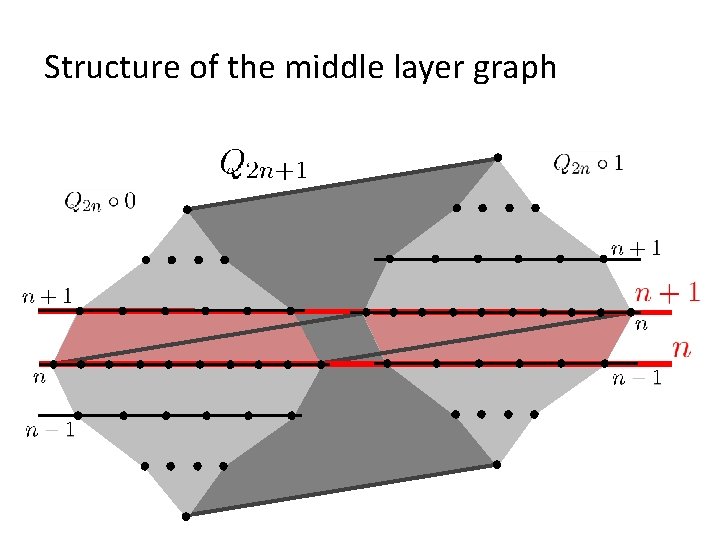
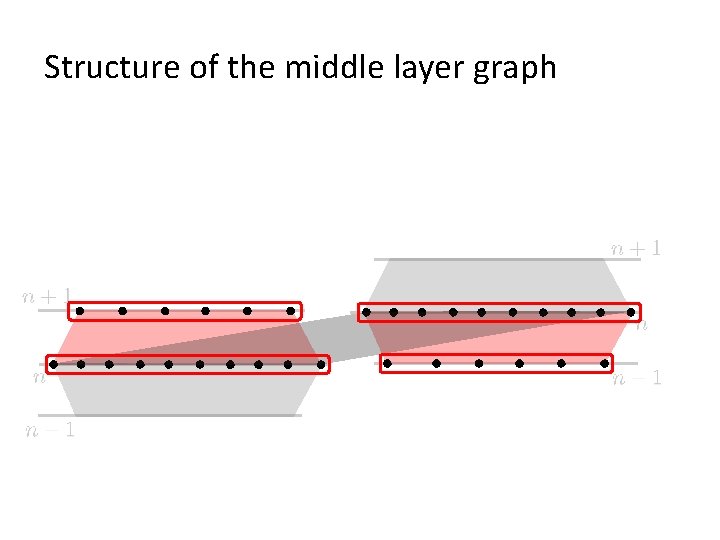
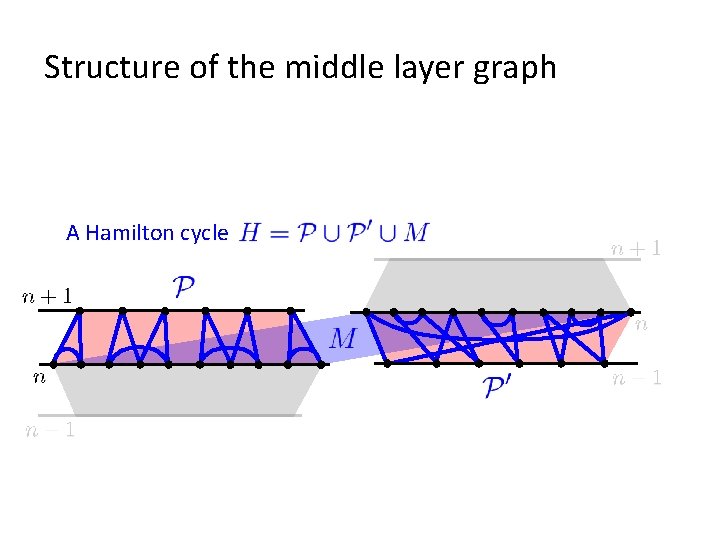
Structure of the middle layer graph

Structure of the middle layer graph

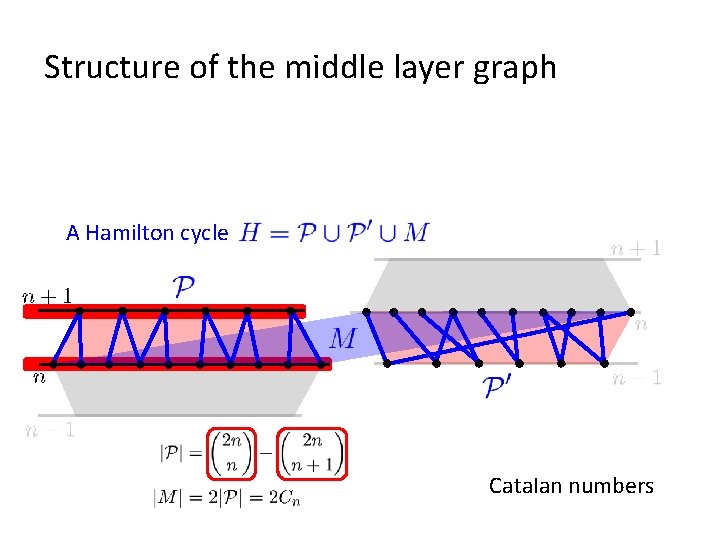
Structure of the middle layer graph A Hamilton cycle Catalan numbers

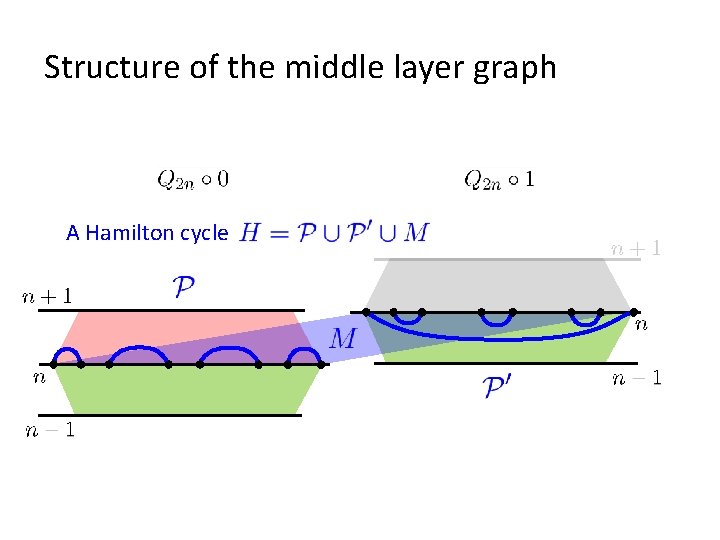
Structure of the middle layer graph A Hamilton cycle

Structure of the middle layer graph A Hamilton cycle

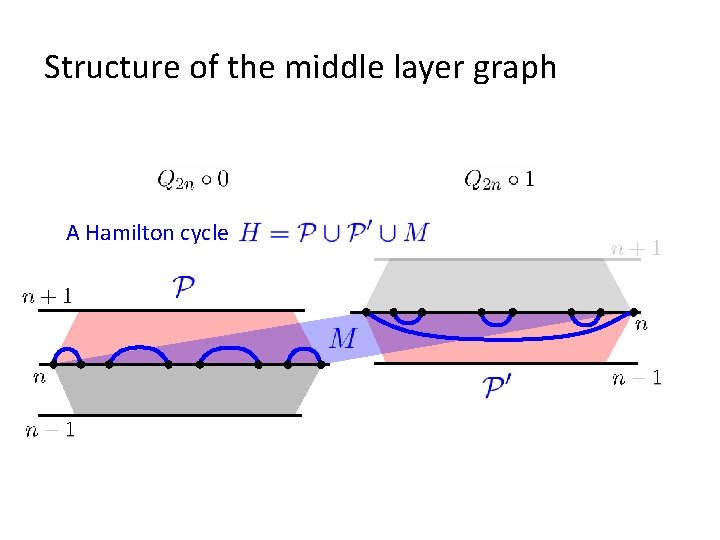
Structure of the middle layer graph A Hamilton cycle

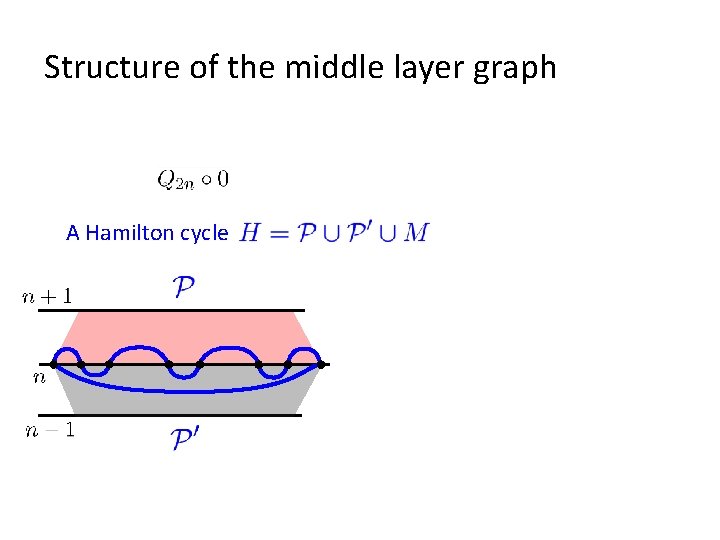
Structure of the middle layer graph A Hamilton cycle

Step 1: Build a 2 -factor Construction from [M. , Weber 12] ? ? ? isomorphism (bit permutation + inversion)

Step 1: Build a 2 -factor Construction from [M. , Weber 12] 2 -factor isomorphism (bit permutation + inversion)

Step 1: Build a 2 -factor Construction from [M. , Weber 12] • parametrizing yields different 2 -factors • essentially one can be analyzed: = plane trees with edges 2 -factor Fundamental problem: varying changes globally

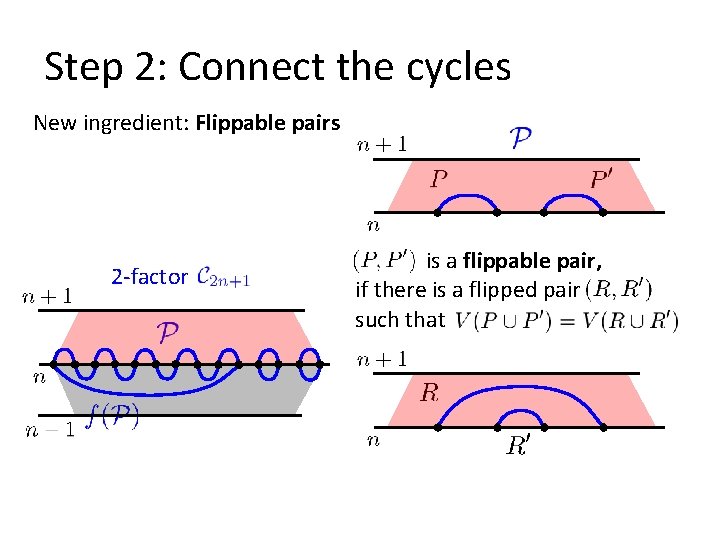
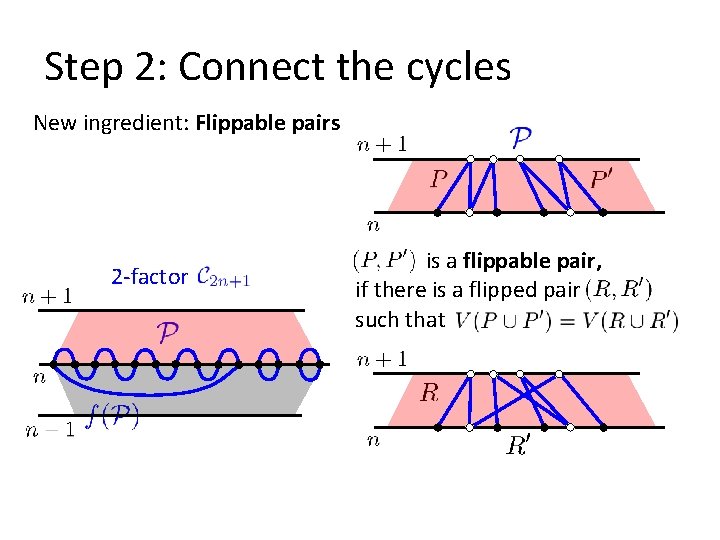
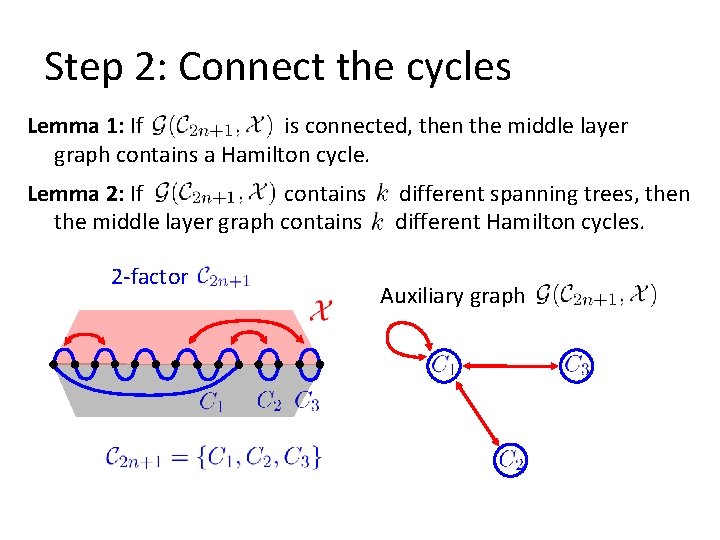
Step 2: Connect the cycles New ingredient: Flippable pairs 2 -factor is a flippable pair, if there is a flipped pair such that

Step 2: Connect the cycles New ingredient: Flippable pairs 2 -factor is a flippable pair, if there is a flipped pair such that

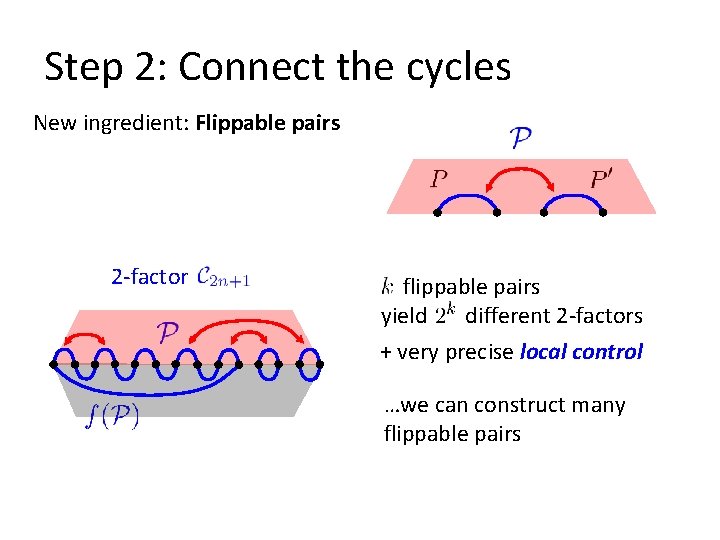
Step 2: Connect the cycles New ingredient: Flippable pairs 2 -factor flippable pairs yield different 2 -factors + very precise local control …we can construct many flippable pairs

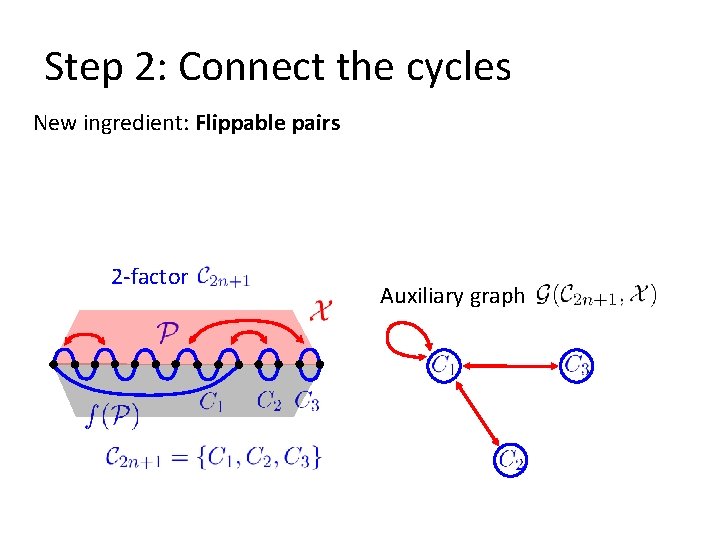
Step 2: Connect the cycles New ingredient: Flippable pairs 2 -factor Auxiliary graph

Step 2: Connect the cycles Lemma 1: If is connected, then the middle layer graph contains a Hamilton cycle. Lemma 2: If contains the middle layer graph contains 2 -factor different spanning trees, then different Hamilton cycles. Auxiliary graph

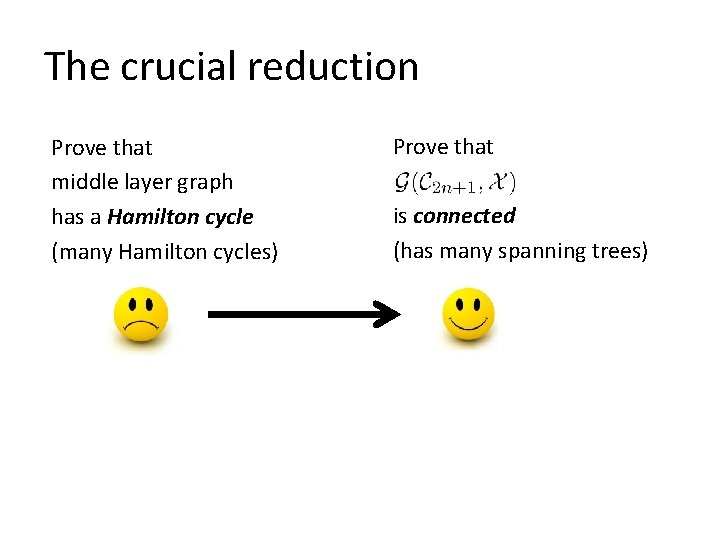
The crucial reduction Prove that middle layer graph has a Hamilton cycle (many Hamilton cycles) Prove that is connected (has many spanning trees)

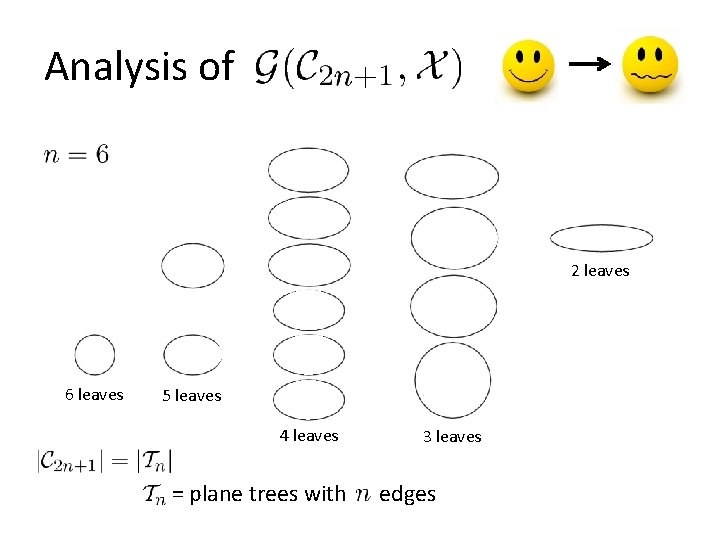
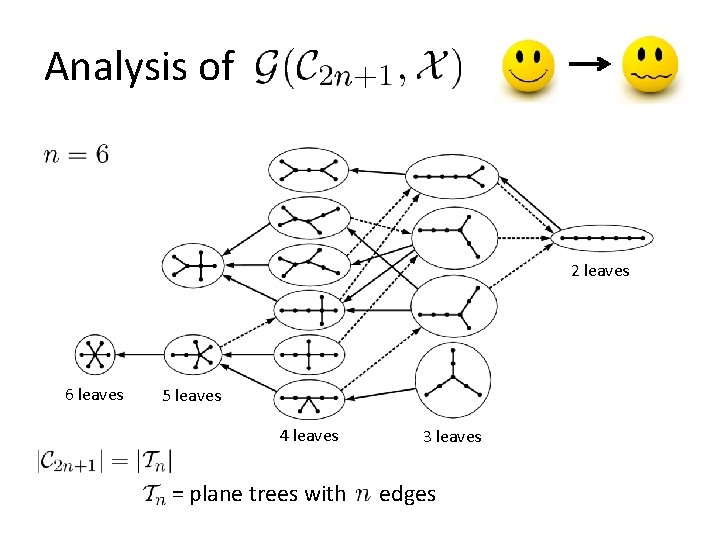
Analysis of 2 leaves 6 leaves 5 leaves 4 leaves = plane trees with 3 leaves edges

Analysis of 2 leaves 6 leaves 5 leaves 4 leaves = plane trees with 3 leaves edges

Thank you!