On symmetric chains and Hamilton cycles Torsten Mtze

On symmetric chains and Hamilton cycles Torsten Mütze (based on joint work with Karl Däubel, Sven Jäger, Petr Gregor, Joe Sawada, Manfred Scheucher, and Kaja Wille)

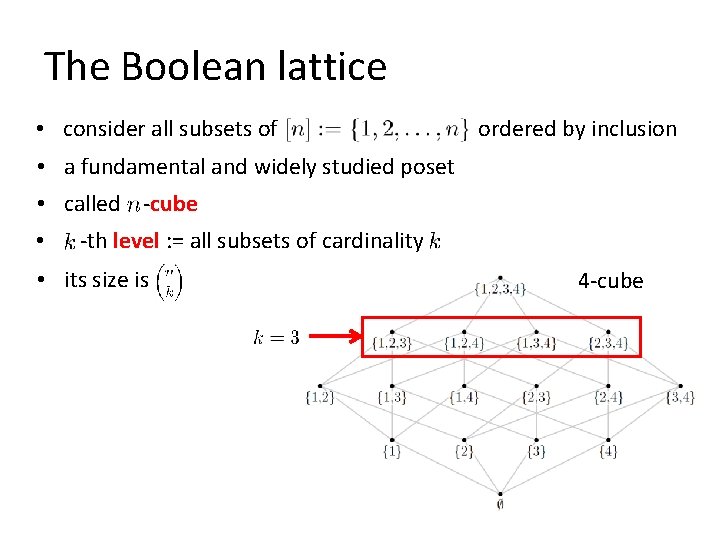
The Boolean lattice • consider all subsets of ordered by inclusion • a fundamental and widely studied poset • called -cube • -th level : = all subsets of cardinality • its size is 4 -cube

The Boolean lattice • consider all subsets of ordered by inclusion • a fundamental and widely studied poset • called -cube • -th level : = all subsets of cardinality • its size is middle level(s) even odd

Chain decompositions Theorem [Sperner 28]: The width (=size of a maximum antichain) of the -cube is given by the size of its middle level(s). Theorem [Dilworth 50]: Any poset can be decomposed into many chains. chain decomposition 4 -cube

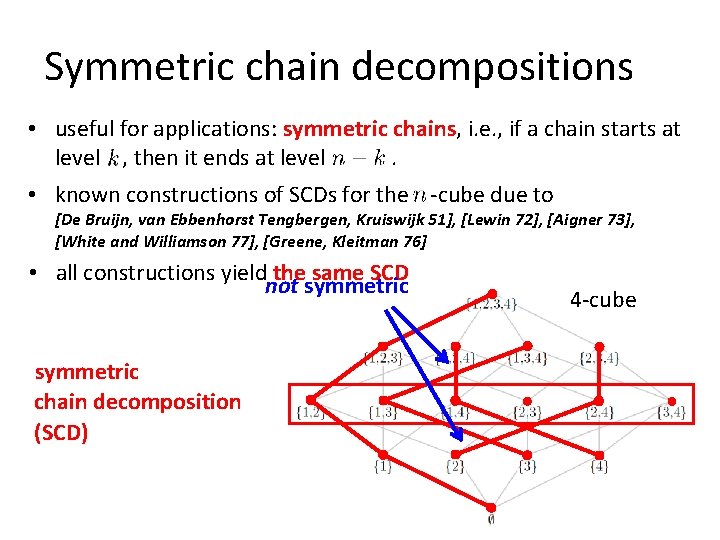
Symmetric chain decompositions • useful for applications: symmetric chains, i. e. , if a chain starts at level , then it ends at level. • known constructions of SCDs for the -cube due to [De Bruijn, van Ebbenhorst Tengbergen, Kruiswijk 51], [Lewin 72], [Aigner 73], [White and Williamson 77], [Greene, Kleitman 76] • all constructions yield the same SCD not symmetric chain decomposition (SCD) 4 -cube

Parenthesis matching • useful for applications: symmetric chains, i. e. , if a chain starts at level , then it ends at level. • known constructions of SCDs for the -cube due to [De Bruijn, van Ebbenhorst Tengbergen, Kruiswijk 51], [Lewin 72], [Aigner 73], [White and Williamson 77], [Greene, Kleitman 76] • all constructions yield the same SCD • ‚parenthesis matching‘ description by [Greene, Kleitman 76] 1001110110 1001110100 100100 0001100100

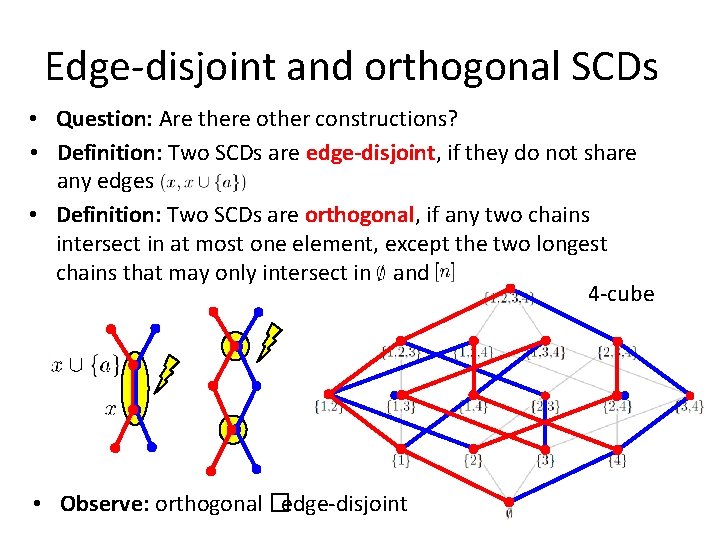
Edge-disjoint and orthogonal SCDs • Question: Are there other constructions? • Definition: Two SCDs are edge-disjoint, if they do not share any edges • Definition: Two SCDs are orthogonal, if any two chains intersect in at most one element, except the two longest chains that may only intersect in and 4 -cube • Observe: orthogonal �edge-disjoint

Edge-disjoint and orthogonal SCDs • Question: How many pairwise edge-disjoint/orthogonal SCDs can we hope for? even • is an upper bound: every SCD uses exactly one of those edges • Conjecture [Shearer, Kleitman 79]: The -cube has pairwise orthogonal SCDs. • Theorem [Shearer, Kleitman 79]: The standard construction and its complements are two orthogonal SCDs. • Theorem [Spink 17]: The -cube has three pairwise orthogonal SCDs for.

Our results Theorem 1: The -cube has four pw. orthogonal SCDs for . Theorem 2: The -cube has five pw. edge-disjoint SCDs for . Proof of Theorem 2: • Product lemma: If the -cube and -cube have edge-disjoint SCDs each, then the -cube has edge-disjoint SCDs. • find five edge-disjoint SCDs for dimensions • Fact: If and are coprime, then every negative integer multiple of and is a non- computer search in the necklace poset Proof of Theorem 1: • similar, but more complicated product lemma due to [Spink 17] • find four orthogonal SCDs for dimensions and

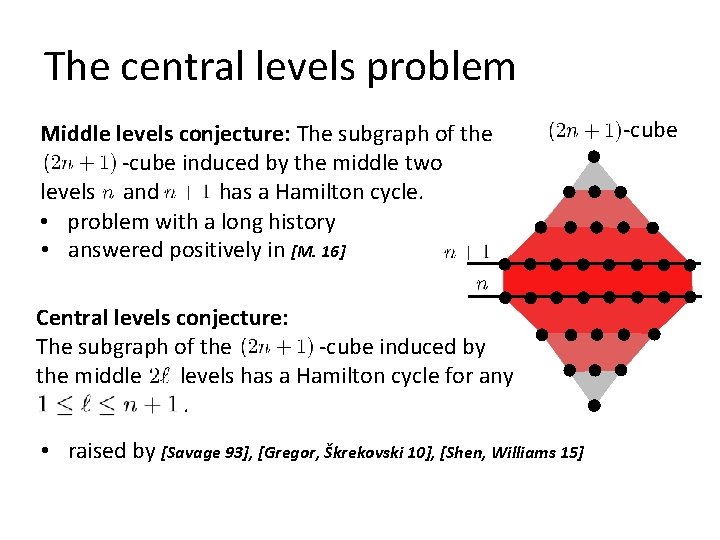
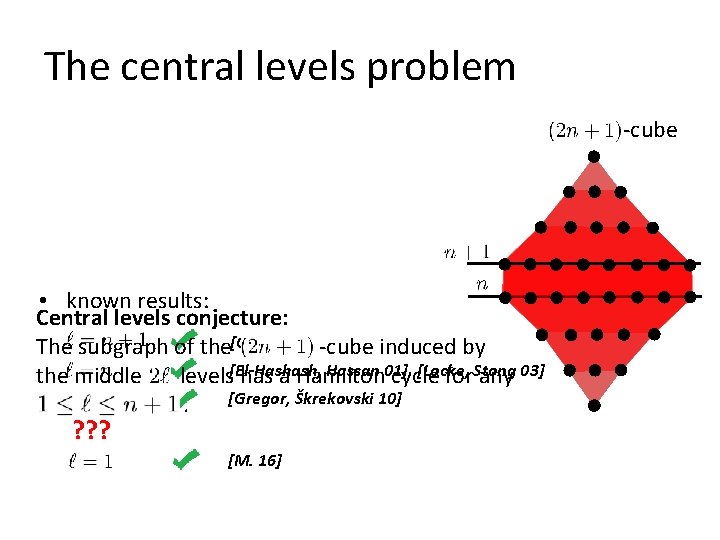
The central levels problem Middle levels conjecture: The subgraph of the -cube induced by the middle two levels and has a Hamilton cycle. • problem with a long history • answered positively in [M. 16] Central levels conjecture: The subgraph of the -cube induced by the middle levels has a Hamilton cycle for any. • raised by [Savage 93], [Gregor, Škrekovski 10], [Shen, Williams 15] -cube

The central levels problem -cube • known results: Central levels conjecture: The subgraph of the[Gray 53] -cube induced by Hassan 01], [Locke, the middle levels[El-Hashash, has a Hamilton cycle for. Stong any 03] [Gregor, Škrekovski 10]. ? ? ? [M. 16]

Our results Theorem 3: The -cube has a Hamilton cycle through the middle four levels ( ) for all. Theorem 4: The -cube has a cycle factor through the middle for all and. spanning collection of disjoint cycles levels

The central levels problem Theorem Proof: 4: The -cube has a cycle factor through the middle. SCDslevels • consider two edge-disjoint for all and • as the. dimension is odd, all chains have odd length, even after restricting to middle levels • taking every second edge yields two edge-disjoint perfect matchings • their union is a cycle factor

Open problems • Conjecture [Shearer, Kleitman 79]: The -cube has pairwise orthogonal SCDs. known: four • we conjecture that the disjoint SCDs. -cube has pairwise edgeknown: five • central levels problem: Can the cycles in the factor be joined to a single Hamilton cycle? first open case: Structure of the cycle factor? middle six levels • efficient algorithms to generate those cycles • exploit new SCD constructions in other applications (Venn diagrams etc. )

Thank you!