Explicit matchings in the middle levels graph Torsten

Explicit matchings in the middle levels graph Torsten Mütze

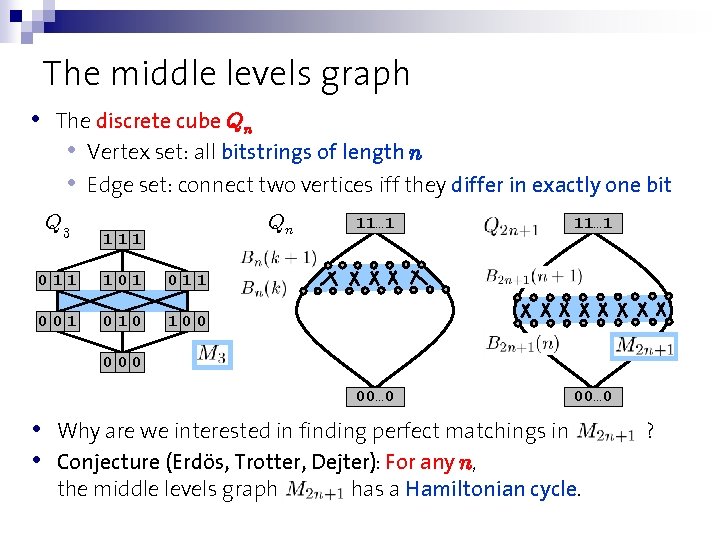
The middle levels graph • The discrete cube Qn • Vertex set: all bitstrings of length n • Edge set: connect two vertices iff they differ in exactly one bit Q 3 Qn 111 011 101 011 001 010 100 11… 1 00… 0 000 • • Why are we interested in finding perfect matchings in Conjecture (Erdös, Trotter, Dejter): For any n, the middle levels graph has a Hamiltonian cycle. ?

What is known about the conjecture • Computer experiments for small n: The conjecture holds for all [Shields, Savage ‘ 06] • The number of vertices of is huge: • General results: For any n, the graph has a cycle containing at least a … • … 0. 893 -fraction of all vertices [Savage, Winkler ‘ 95] • … (1 -o(1))-fraction of all vertices [Johnson ‘ 04] One possible approach: 011 101 011 • Any Hamiltonian cycle in is the 001 010 100 union of two perfect matchings • Find large families of perfect matchings in and try to combine two of them • This talk: review and compare several known constructions

Perfect matchings exist • • is bipartite and (n+1)-regular By Hall‘s theorem a perfect matching in exists, even a 1 -factorization into n+1 disjoint perfect matchings 11100 11010 11000 10100 n n+1 110010 10101 10011 01110 01101 01011 00111 10001 01100 01010 01001 00110 00101 00011

Perfect matchings exist • • is bipartite and (n+1)-regular By Hall‘s theorem a perfect matching in exists, even a 1 -factorization into n+1 disjoint perfect matchings 11100 11010 11000 10100 110010 10101 10011 01110 01101 01011 00111 10001 01100 01010 n n+1 • Show me an ‚explicit‘ matching! 01001 00110 00101 00011

Construction 1 • An inductive construction due to [Greene, Kleitman ’ 76], [de Bruijn, Tengbergen, Kruyswijk ’ 51]: 11… 1 • It yields something much stronger, a symmetric chain decomposition of Qn • For odd n, the chains induce a perfect matching in the middle levels graph 00… 0 11 10 01 00 Qn

Construction 1 • An inductive construction due to [Greene, Kleitman ’ 76], [de Bruijn, Tengbergen, Kruyswijk ’ 51]: 11… 1 • It yields something much stronger, a symmetric chain decomposition of Qn • For odd n, the chains induce a perfect matching in the middle levels graph 00… 0 11 10 01 00 Qn

Construction 1 • An inductive construction due to [Greene, Kleitman ’ 76], [de Bruijn, Tengbergen, Kruyswijk ’ 51]: 11… 1 • It yields something much stronger, a symmetric chain decomposition of Qn • For odd n, the chains induce a perfect matching in the middle levels graph 00… 0 11 10 01 00 • Disadvantage: need to know previous construction steps Qn

Construction 2 • A greedy construction due to [Aigner ’ 73]: • In each layer sort vertices lexicographically: x < y if first at first position where they differ xi=1 and yi=0 • Go through vertices in and greedily match them to first unmatched vertex in (if possible) 1100 0000 • • 1000 1010 1110 0100 1001 1101 0010 0110 1011 0001 0111 Qn 1111 0011 Need to prove that this always yields a maximum matching (i. e. a perfect matching in the middle levels graph) Disadvantage: need to know previously matched vertices

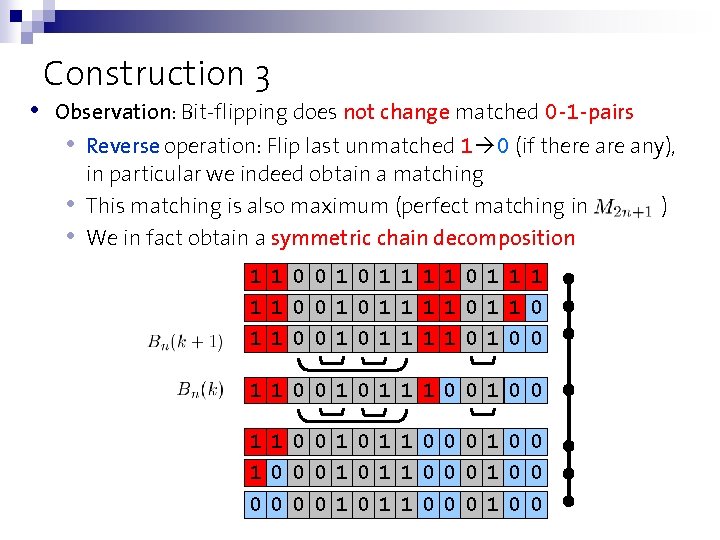
• Construction 3 An explicit construction due to [Aigner ’ 73], [Greene, Kleitman ’ 76]: • Repeatedly match closest 0 - and 1 -digits • Flip first unmatched 0 1 (if there any) 11001011110100 11001011100100

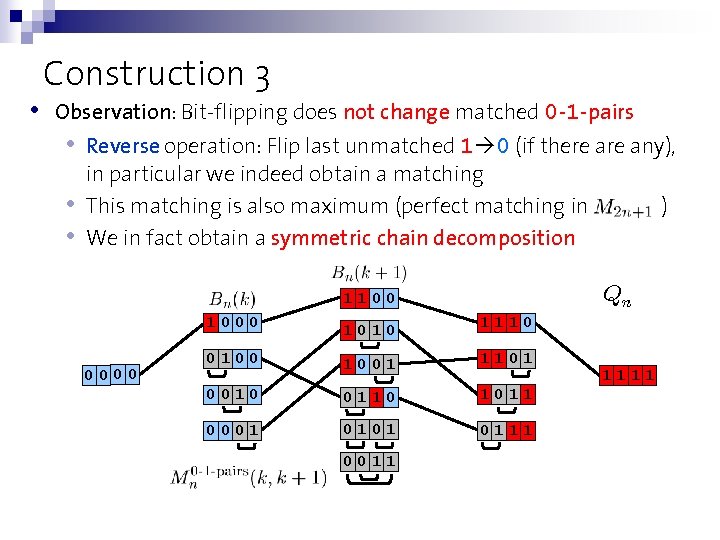
• Construction 3 Observation: Bit-flipping does not change matched 0 -1 -pairs • Reverse operation: Flip last unmatched 1 0 (if there any), • • in particular we indeed obtain a matching This matching is also maximum (perfect matching in We in fact obtain a symmetric chain decomposition 11001011110110 11001011110100 11001011100100 11001011000100 10001011000100 00001011000100 )

• Construction 3 Observation: Bit-flipping does not change matched 0 -1 -pairs • Reverse operation: Flip last unmatched 1 0 (if there any), • • in particular we indeed obtain a matching This matching is also maximum (perfect matching in We in fact obtain a symmetric chain decomposition Qn 1100 0000 1010 1110 0100 1001 1101 0010 0110 1011 0001 0111 0011 ) 1111

Equivalence of the constructions • Theorem: All 3 constructions yield the same matchings (and SCDs): Construction 1: inductive SCD • Construction 2: greedy matching Construction 3: explicit 0 -1 -pairs approach Depending on the context, each of the descriptions has its merits

How to obtain more matchings • So far we have found only one explicit matching in the middle levels graph • • How to obtain more? Idea: Apply automorphisms of • So how many different matchings do we get? : bit permutations + bit inversion many different matchings, called lexicographic matchings Bit inversion does not produce any new matchings Cyclic bit shifts yield the same matching

Do they yield a Hamiltonian cycle? • • • Theorem ([Duffus, Sands, Woodrow ’ 88]): For , no two lexicographic matchings form a Hamiltonian cycle in. Not true for the trivial case (2 lexicographic matchings): 011 101 011 001 010 100 Larger families of explicit matchings?

• Lexical Matchings Superset of the lexicographic matchings 110010100 [Kierstead, Trotter ‘ 88] u(x) : = number of upsteps below the x-axis 4 i-lexical matching : = for each flip the bit for which u(x)=i 110010100 1 110010100 2 The i-lexical 110010100 matchings, i=0, 1, …, n, 3 form a 1 -factorization of 110010100 0

• Lexical Matchings Superset of the lexicographic matchings 110010100 [Kierstead, Trotter ‘ 88] u(x) : = number of upsteps below the x-axis 2 110011100 Other potential partners for y: 010011100 1 100011100 3 110001100 0 11000 4 i-lexical matching : = for each flip the bit for which u(x)=i by the same argument as before So we indeed get a matching

• [Kierstead, Trotter ‘ 88] Lexical Matchings Superset of the lexicographic matchings: 0 -lexical matching = lexicographic matching • Behavior under automorphisms of the middle levels graph: 0 -lexical matching different matchings (the lexicographic matchings) 1 -lexical matching another different matchings n/2 -lexical matching another different matchings n-lexical matching • No new matchings many different matchings, called lexical matchings Do two of them form a Hamiltonian cycle? n=1, 2, 3: yes, n=4: no, n>4: not known

• • Outlook Modular matchings [Duffus, Kierstead, Snevily ‘ 94] defined via an algebraic construction Similarly large class like the lexical matchings, distinct from the lexical matchings Similar behavior under automorphisms of the middle levels graph Do two of them form a Hamiltonian cycle? Not known.

Thank you! Questions?