Vertex Covers and Matchings Given an undirected graph

Vertex Covers and Matchings • Given an undirected graph G=(V, E), – a vertex cover of G is a subset of the vertices C such that for every edge (i, j) in E i is in C and/or j is in C. -a matching in G is a subset of the edges M such that no two edges in M share the same vertex.

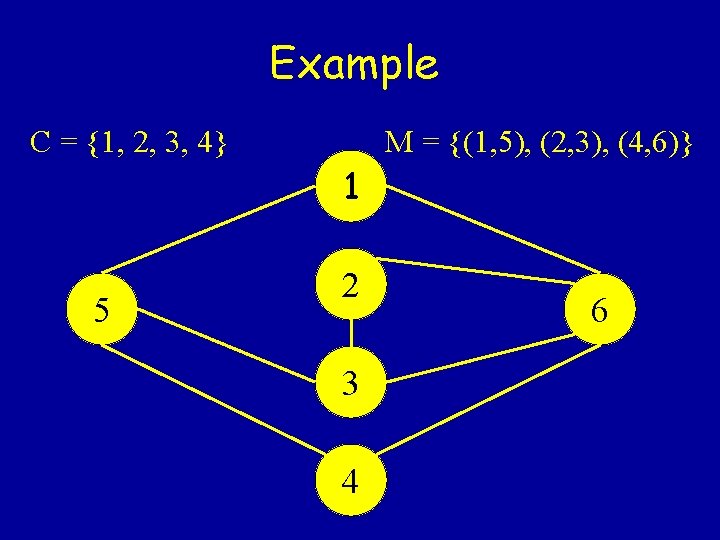
Example C = {1, 2, 3, 4} M = {(1, 5), (2, 3), (4, 6)} 1 5 2 3 4 6

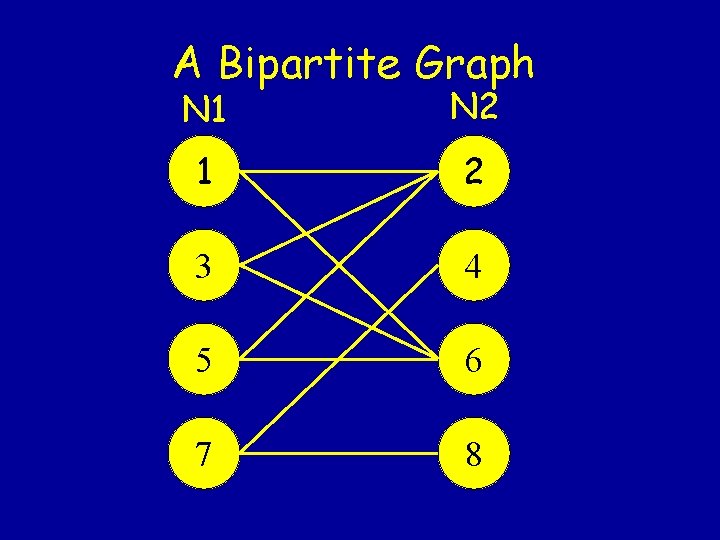
Maximum Cardinality Matching • Find the largest matching in a given graph G. • Tricky (put polynomial) in general, but “easy” in a bipartite graph. – A bipartite network has two sets of nodes N 1 and N 2 such that all edges have one endpoint in N 1 and the other in N 2.

A Bipartite Graph N 1 N 2 1 2 3 4 5 6 7 8

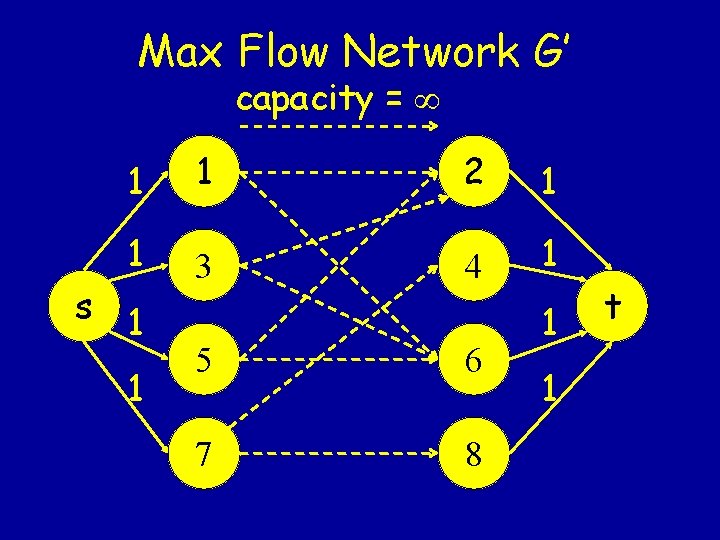
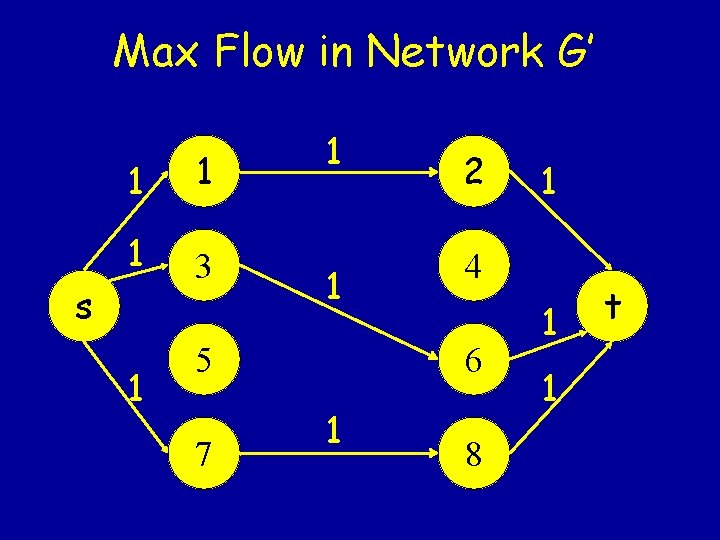
Max Flow Network G’ capacity = 1 1 2 1 1 3 4 1 s 1 1 5 6 7 8 1 1 t

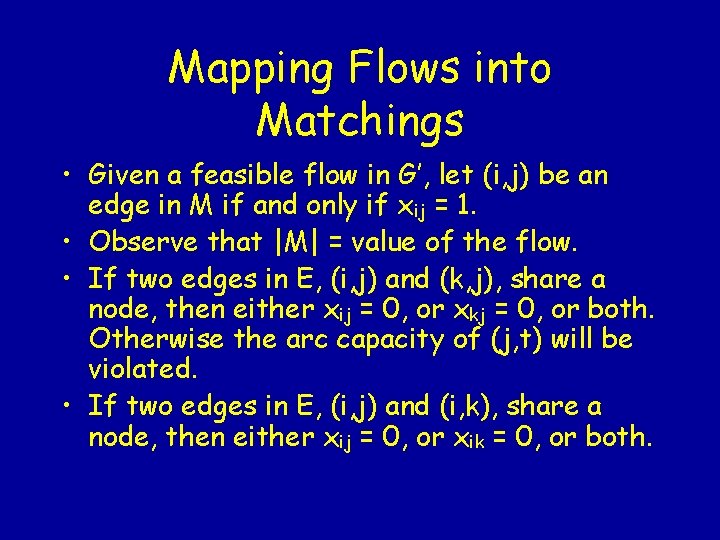
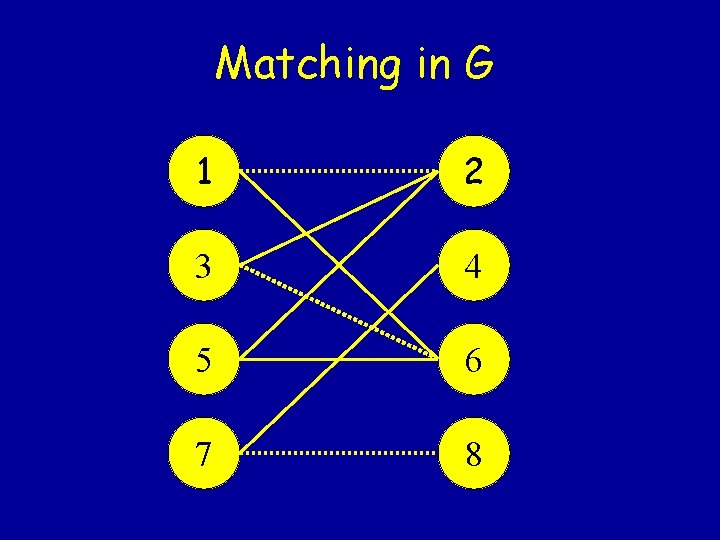
Mapping Flows into Matchings • Given a feasible flow in G’, let (i, j) be an edge in M if and only if xij = 1. • Observe that |M| = value of the flow. • If two edges in E, (i, j) and (k, j), share a node, then either xij = 0, or xkj = 0, or both. Otherwise the arc capacity of (j, t) will be violated. • If two edges in E, (i, j) and (i, k), share a node, then either xij = 0, or xik = 0, or both.

Mapping Matchings into Flows • Start with a zero flow. • If (i, j) is an edge in M, then let xsi=1, xij=1, and xjt=1. • Consider a pair of matched nodes i and j. – The flow x sends exactly one unit of flow to node i on arc (s, i) and exactly one unit of flow into the sink on arc (j, t) – Thus, a matching of size |M| gives a feasible s -t flow of value |M|.

Max Flow in Network G’ 1 1 1 3 s 1 1 1 5 7 2 4 6 1 1 8 1 1 t

Matching in G 1 2 3 4 5 6 7 8

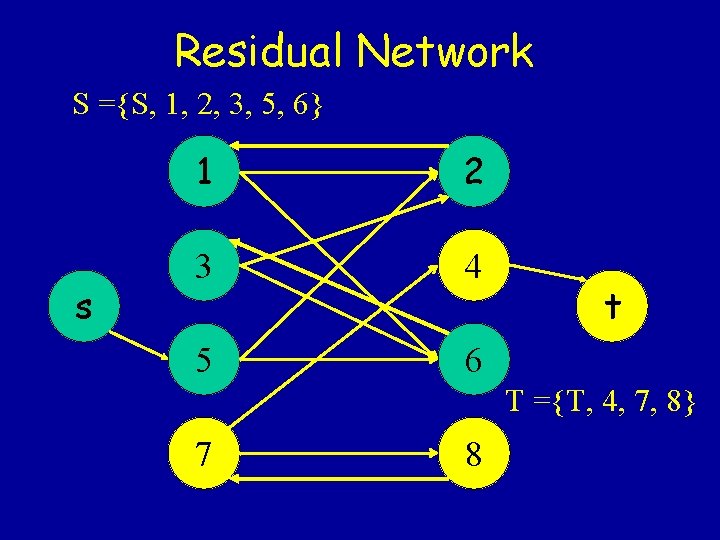
Residual Network S ={S, 1, 2, 3, 5, 6} s 1 2 3 4 5 6 t T ={T, 4, 7, 8} 7 8

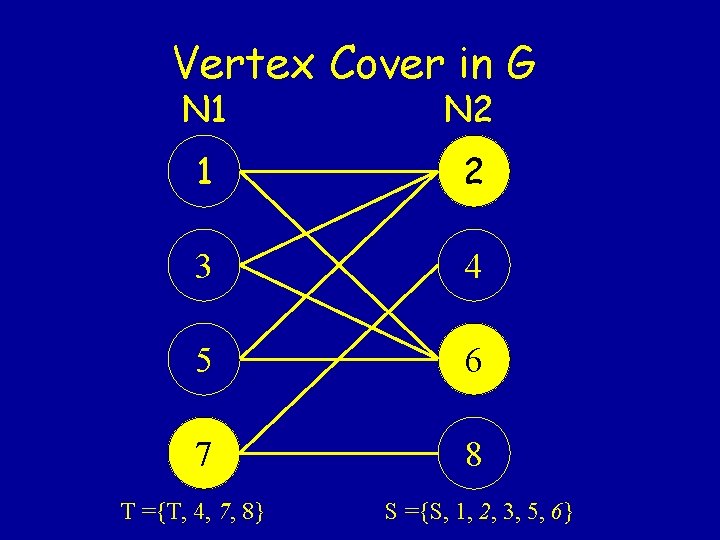
Minimum Cardinality Vertex Covers • Find a vertex cover with a minimum number of nodes. • Hard in general, but polynomial in bipartite graphs. – Solve max flow problem as described earlier and find min cut [S, T]. – C = {i in N 1 T} {i in N 2 S} is a minimum cardinality vertex cover.

Vertex Cover in G N 1 N 2 1 2 3 4 5 6 7 8 T ={T, 4, 7, 8} S ={S, 1, 2, 3, 5, 6}

Correctness of Vertex Cover Result N 1 N 2 j in N 2 S N 1 S s j 1 t 1 N 2 T i i in N 1 T can’t be in min cut

Correctness of Vertex Cover Result • Let [S, T] be a finite cut in G. • Claim: C = {i in N 1 T} {i in N 2 S} is a vertex cover. – Suppose not. – This implies there is some edge (a, b) such that a is in N 1 and S, and b is in N 2 and T. – Since a is in N 1 and b is in N 2 capacity (a, b) = . – But (a, b) goes from s to t. So, u[S, T] = .

Correctness of Vertex Cover Result • The [S, T] be a finite cut in G. • Claim: C = {i in N 1 T} {i in N 2 S} is a vertex cover such that|C|=u[S, T]. • Theorem for Bipartite Graphs: The cardinality of a maximum-size matching is equal to the cardinality of a minimum-size vertex cover.