Practice Quiz next time Geometry Topology One quiz

Practice § Quiz next time – Geometry – Topology § One quiz will not count towards your grade – The one with lowest grade – If you missed a class, you don’t need to make up Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 1

Topology in 1 D § We consider subsets S of the real line, such as • S=[2, 3[, which includes all real numbers x: 2≤x<3 • S=]2, 3], which includes all real numbers x: 2<x≤ 3 • S=[5], which contains only the number 5 • S=[2, 3[ + [5], which includes real numbers x: 2≤x<3 and also the number 5 § The operators complement (!), boundary (. b), interior (. i), exterior (. e), closure (. k), regularization (. r) are relative to the real line § Hence if S=[2, 3[, then S. i=]2, 3[, excluding the value 2. Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 2

Q 1 § S = [2, 3[ + ]3, 4[ + [5], What is S. i (interior)? Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 3

R 1 § S = [2, 3[ + ]3, 4[ + [5], S. i = ]2, 3[ + ]3, 4[ Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 4

Q 2 § S = [2, 3[ + ]3, 4[ + [5], What is S. b (boundary)? Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 5

R 2 § S = [2, 3[ + ]3, 4[ + [5], S. b = [2] + [3] + [4] + [5] Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 6

Q 3 § S = [2, 3[ + ]3, 4[ + [5], What is S. k (closure)? Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 7

R 3 § S = [2, 3[ + ]3, 4[ + [5], S. k = [2, 4] + [5] Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 8

Q 4 § S = [2, 3[ + ]3, 4[ + [5], What is S. r (regularization)? Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 9

R 4 § S = [2, 3[ + ]3, 4[ + [5], S. r = S. i. k = [2, 4] Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 10

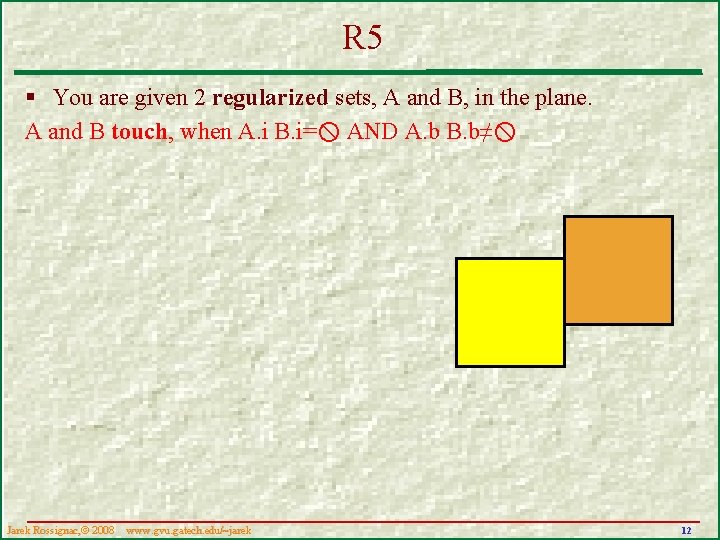
Q 5 § You are given 2 regularized sets, A and B, in the plane. Use. i, . b, . k, . e…, and Boolean operators to express the condition that A and B touch, even though they do not interfere. Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 11

R 5 § You are given 2 regularized sets, A and B, in the plane. A and B touch, when A. i B. i= AND A. b B. b≠ Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 12

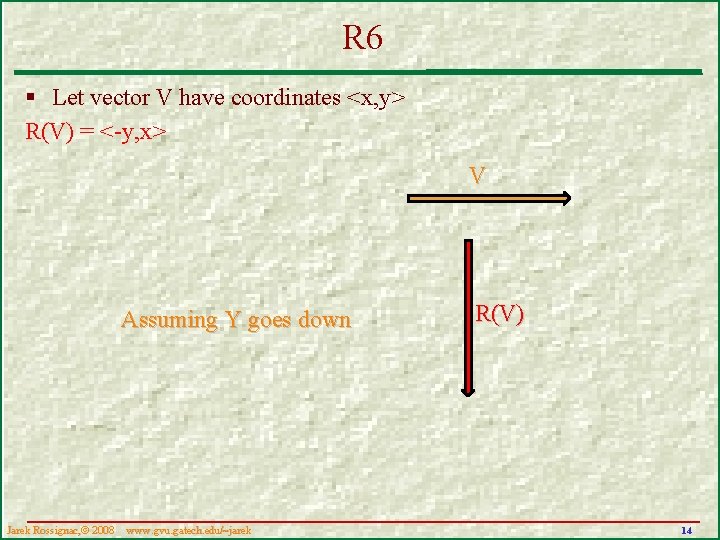
Q 6 § Let vector V have coordinates <x, y> What are the coordinates of R(V)? Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 13

R 6 § Let vector V have coordinates <x, y> R(V) = <-y, x> V Assuming Y goes down Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek R(V) 14

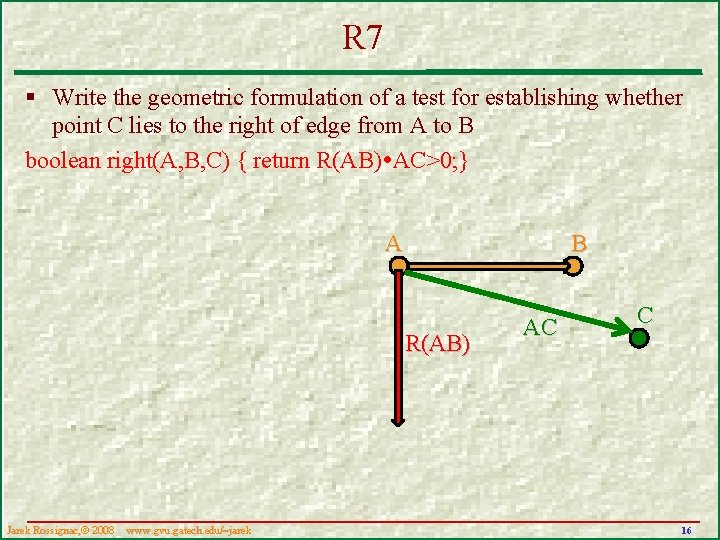
Q 7 § Write the geometric formulation of a test for establishing whether point C lies to the right of edge from A to B boolean right(A, B, C) { return … } A B C Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 15

R 7 § Write the geometric formulation of a test for establishing whether point C lies to the right of edge from A to B boolean right(A, B, C) { return R(AB) AC>0; } A B R(AB) Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek AC C 16

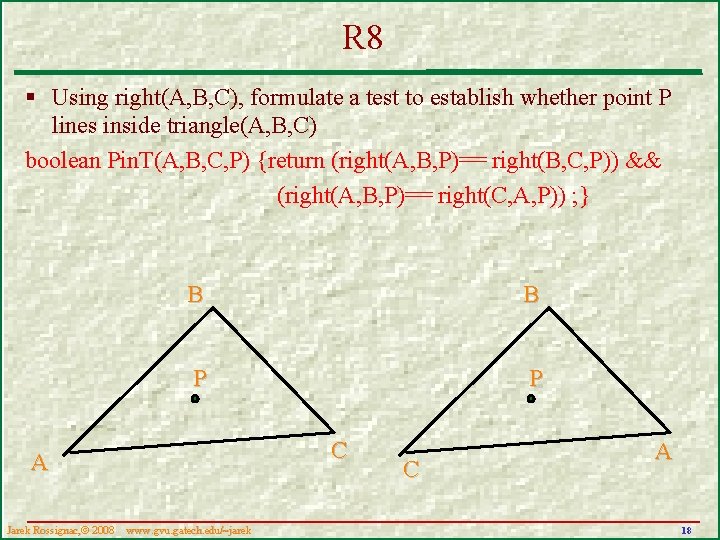
Q 8 § Using right(A, B, C), formulate a test to establish whether point P lines inside triangle(A, B, C) boolean Pin. T(A, B, C, P) {return … ; } B P A Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek C 17

R 8 § Using right(A, B, C), formulate a test to establish whether point P lines inside triangle(A, B, C) boolean Pin. T(A, B, C, P) {return (right(A, B, P)== right(B, C, P)) && (right(A, B, P)== right(C, A, P)) ; } B B P P C A Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek C A 18

Q 9 § Write the geometric formulation of a test to assess whether point C lies in the relative interior of edge (A, B). boolean Pin. E(A, B, C) {return … ; } A B C Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 19

R 9 § Write the geometric formulation of a test to assess whether point C lies in the relative interior of edge (A, B). boolean Pin. E(A, B, C) {return (R(AB) AC==0) && (0 < AB AC) && (AB AC < AB AB) ; } A B C Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 20

Q 10 § Write the geometric formulation of a test to assess whether the closed edges (A, B) and (C, D) are disjoint (no intersection). boolean disjoint. Edges(A, B, C, D) { return …} Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 21

R 10 § Write the geometric formulation of a test to assess whether the closed edges (A, B) and (C, D) are disjoint (no intersection). boolean disjoint. Edges(A, B, C, D) { return (right(A, B, C) == right(A, B, D)) || (right(C, D, A) == right(C, D, A)) } Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 22

Q: Point in polygon test § How to test whether a point Q lies in polygon P? A C Q P B D Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 23

R: Point in polygon test § How to test whether a point Q lies in polygon P? § Construct a ray R from Q that does not hit any vertex § Compute the number x of intersections or R and b. P – One edge at a time, in any order – Works even if P has holes or several components A § Return x %2 == 1 C Q R P B D Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 24

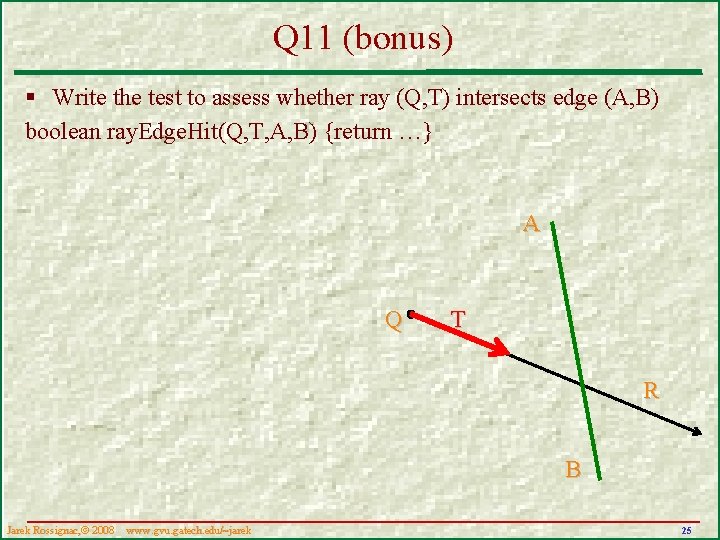
Q 11 (bonus) § Write the test to assess whether ray (Q, T) intersects edge (A, B) boolean ray. Edge. Hit(Q, T, A, B) {return …} A Q T R B Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 25

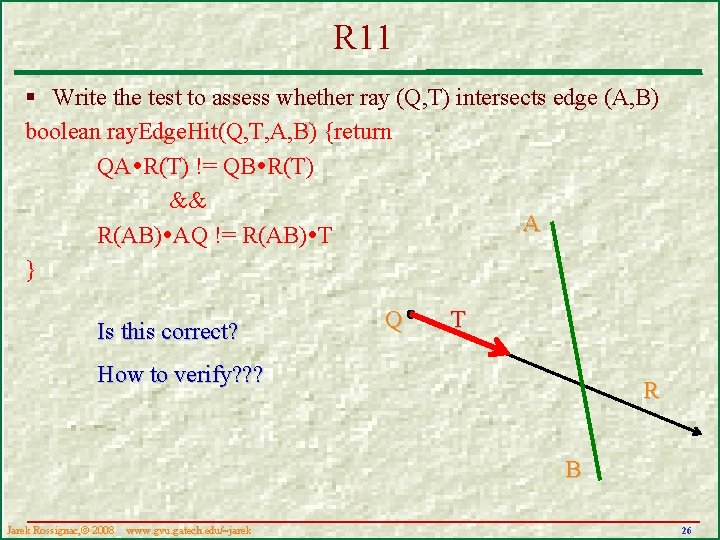
R 11 § Write the test to assess whether ray (Q, T) intersects edge (A, B) boolean ray. Edge. Hit(Q, T, A, B) {return QA R(T) != QB R(T) && A R(AB) AQ != R(AB) T } Is this correct? Q T How to verify? ? ? R B Jarek Rossignac, 2008 www. gvu. . gatech. edu/~jarek 26