Physical Property Analysis Physical Properties A physical property



















- Slides: 19


Physical Property Analysis

Physical Properties A physical property is a property that can be observed or measured without changing the identity of the matter. Examples of Physical Properties: Volume Density Color Surface Area Centroid Moment of Inertia Mass Odor Temperature Melting Point Viscosity Electric Charge

Physical Property Analysis The size, volume, surface area, and other properties associated with a solid model are often part of the design constraints or solution criteria. The following are physical properties presented in typical solid modeling programs: Volume Density Mass Surface Area Center of Gravity Moment of Inertia Product of Inertia Radii of Gyration Principal Axes Principal Moments Length

Physical Properties In this lesson you will investigate the following physical properties: • • Volume Surface Area Density Mass

Volume • Volume is the amount of three-dimensional space occupied by an object or enclosed within a container • Design engineers use volume to determine the amount of material needed to produce a part • Different formulas for different shapes Rectangular Prism V=Hx. Wx. L V = 4” x 8” V = 128 in. 3 4 4 8

Volume in Cubic Units Measure volume using cubic units: It is imperative to keep your units the same when measuring and calculating volume. • • Cubic inches (in. 3) Cubic feet (ft 3) Cubic yards (yds 3) Cubic centimeters (cm 3) • Cubic meters (m 3)

Volume Formulas for Prisms, Cylinders, Pyramids, or Cones If B is the area of the base of a prism, cylinder, pyramid, or cone and H is the height of the solid, then the formula for the volume is V = BH Note: You will need to calculate the area of the shape for the base of the prism. For example: If the solid is a triangular prism, then you will need to calculate the area of the triangle for the base and then calculate the volume.

Area Formulas for Bases of Prisms, Cylinders, and Pyramids Rectangular Prism – base is rectangle, therefore A = length * width or A = lw Cylinder – base is a circle, therefore A = pi * radius of circle squared or A = πr 2 Square Pyramid – base is a square, therefore A = length * width or A = lw or side squared since the sides are the same on a square or A = s 2

Volume of a Cone A Special Case • • A cone is 1/3 of a cylinder The base of a cylinder is a circle The area of a circle is A=πr 2 Therefore, the formula for the volume of a cone is V= 1/3 Ah where A=πr 2 and h is the height of the cone

Density • Density is defined as mass per unit volume. • Density is different for every material and can be found in a machinist handbook.

Mass • Mass is the amount of matter in an object or the quantity of the inertia of the object. • Many materials are purchased by weight; to find weight, you need to know the mass. Polypropylene has a density of. 035 lb/in. 3 and Using the volume from the previous example: V = 128 in. 3 Mass = Volume x Density Mass = 128 in. 3 x. 035 lb/in. 3 Mass = 4. 48 lb

Surface Area • Surface area is the squared dimensions of the exterior surface. • Surface area is important when determining coatings and heat transfer of a part. A= 4 in. x 4 in. = 16 in. 2 B= 4 in. x 8 in. = 32 in. 2 A B C= 4 in. x 8 in. = 32 in. 2 C D= 4 in. x 8 in. = 32 in. 2 D E F E= 4 in. x 8 in. = 32 in. 2 F= 4 in. x 4 in. = 16 in. 2 A + B+ C + D+ E + F = 160 in. 2

To start the Mass Property function, right click the solid model name in the Browser. Pick Properties Mass Property values will be used for predicting material quantity needed for production, finishing, packaging, and shipping.

Additional Physical Properties

Center of Gravity • A 3 D point where the total weight of the body may be considered to be concentrated. • The average location of an object. • If an object rotates when thrown it rotates about its center of gravity. • An object can be balance on a sharp point placed directly beneath its center of gravity

Centroid • A 3 D point defining the geometric center of a solid. • Do not confuse centroid with the center of gravity. – The two only exist at the same 3 D point when the part has uniform geometry and density.

Principal Axes • The lines of intersection created from three mutually perpendicular planes, with the three planes’ point of intersection at the centroid of the part. The X, Y, and Z axes show the principal axes of the ellipsoid.

Sources Brodinski, K. G. (1989). Engineering materials properties and selection. Prentice Hall, Inc. : Englewood Cliffs, NJ. Budinski, K. G. (1992). Engineering materials (4 th Ed. ). Prentice Hall, Inc. : Englewood Cliffs, NJ. Gere, J. M. , & Timoshenko, S. P. (1997). Mechanics of materials. PWS Publishing Company: Boston. Lockhart, S. D. , & Johnson, C. M. (1999). Engineering design communication: Conveying design through graphics (Preliminary Ed. ). Addison Wesley Longman, Inc. : Reading, MA. Madsen, D. A. , Shumaker, T. M. , Turpin, J. L. , & Stark, C. (1994). Engineering design and drawing (2 nd Ed. ). Delmar Publishers Inc. : Albany.
 Physical property and chemical property
Physical property and chemical property Extensive and intensive examples
Extensive and intensive examples Extensive and intensive properties
Extensive and intensive properties Commutative and associative properties
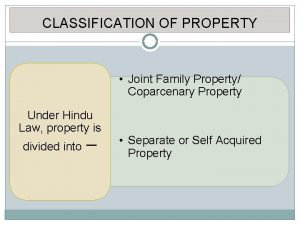
Commutative and associative properties Classification of property under hindu law
Classification of property under hindu law Physical properties of amines
Physical properties of amines Chemical properties of alkenes
Chemical properties of alkenes Physical properties of sulphuric acid
Physical properties of sulphuric acid Physical properties of a solid
Physical properties of a solid A scientist performs an experiment, and an actor performs a
A scientist performs an experiment, and an actor performs a Physical property of starch
Physical property of starch Physical properties of seawater
Physical properties of seawater Thermophysical properties of dental materials
Thermophysical properties of dental materials Lesson outline lesson 2 - physical properties answer key
Lesson outline lesson 2 - physical properties answer key Chemical properties of cardboard
Chemical properties of cardboard Physical changes examples
Physical changes examples What are the physical properties of phosphorus
What are the physical properties of phosphorus Physical properties of paint
Physical properties of paint The physical properties of metals include luster and
The physical properties of metals include luster and Anything defintion
Anything defintion