Parameter Sensitivity in Hydrologic Modeling Tanya Hoogerwerf March

Parameter Sensitivity in Hydrologic Modeling Tanya Hoogerwerf March 7 th, 2002

Outline § Flood discharge calculation overview § Problem statement and research objectives § Case studies § Sensitivity analysis of hydrologic parameters § Conclusions

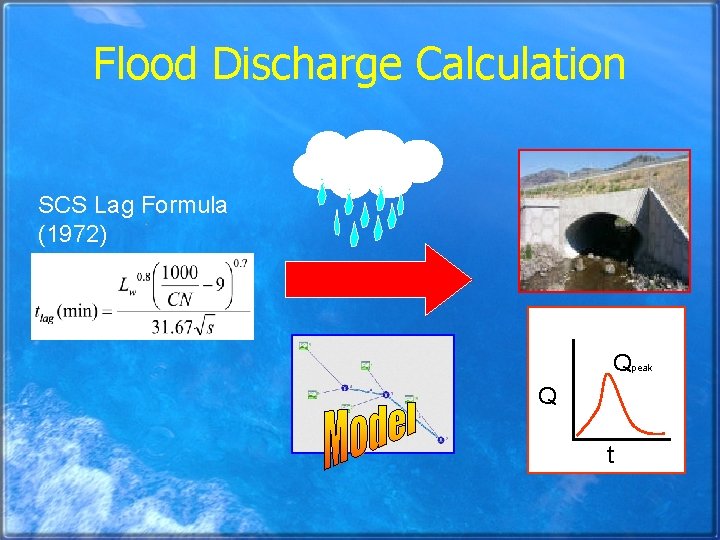
Flood Discharge Calculation

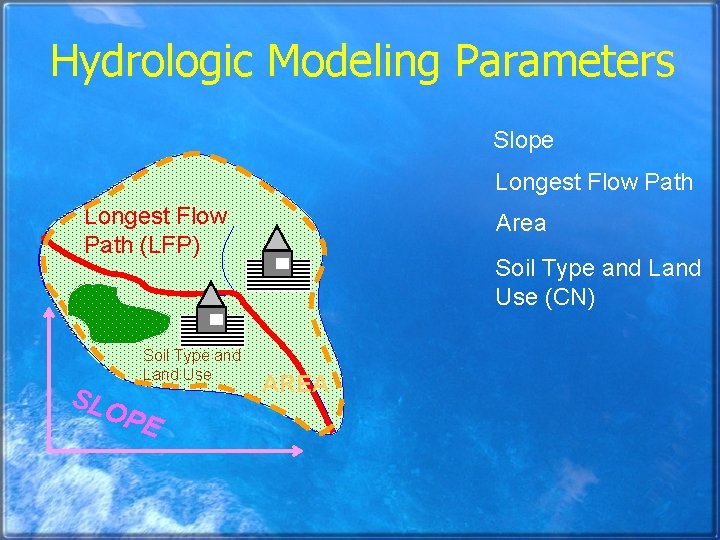
Hydrologic Modeling Parameters Slope Longest Flow Path (LFP) SLO Soil Type and Land Use PE Area Soil Type and Land Use (CN) AREA

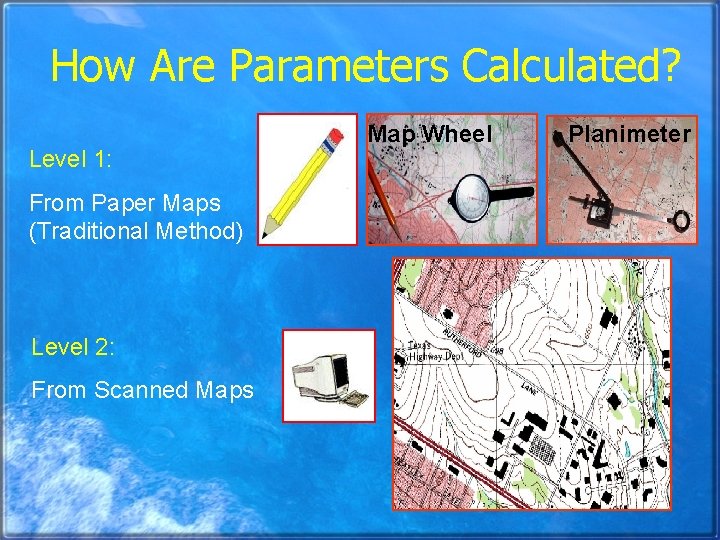
How Are Parameters Calculated? Level 1: From Paper Maps (Traditional Method) Level 2: From Scanned Maps Map Wheel Planimeter

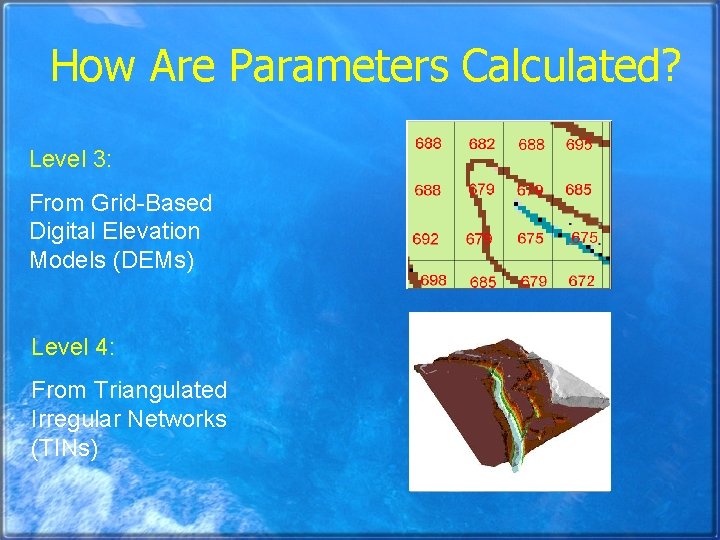
How Are Parameters Calculated? Level 3: From Grid-Based Digital Elevation Models (DEMs) Level 4: From Triangulated Irregular Networks (TINs)

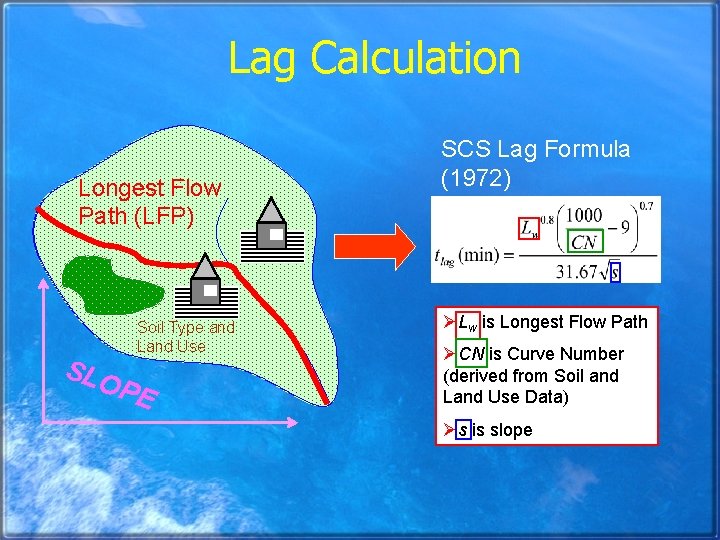
Lag Calculation Longest Flow Path (LFP) SLO Soil Type and Land Use PE SCS Lag Formula (1972) ØLw is Longest Flow Path ØCN is Curve Number (derived from Soil and Land Use Data) Øs is slope

Flood Discharge Calculation SCS Lag Formula (1972) Qpeak Q t

Problem Statement Differences encountered in lag results between traditional methods and automated methods Automated Methods Traditional Methods

Research Objectives § For traditional and automated processes, determine § Sources of error § Range of errors § Significance of errors

Outline § Flood discharge calculation overview § Problem statement and research objectives § Case studies § Sensitivity analysis of hydrologic parameters § Conclusions

What Was Used to Test? § § Set up the four levels of case studies 3 differently sized areas 0. 5 mi 2 1. 6 mi 2 8. 8 mi 2

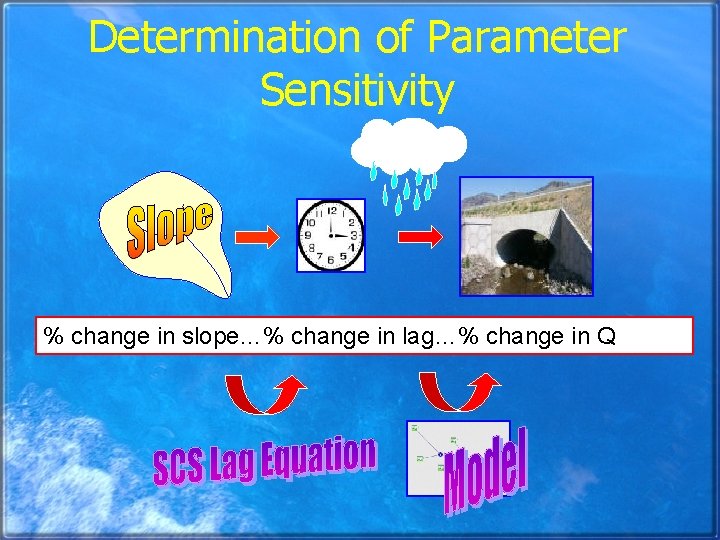
Determination of Parameter Sensitivity % change in slope…% change in lag…% change in Q

Case 1: Measurement From Paper Maps

Case II: On Screen From Raster Maps

Case IIIA: 10 m and 30 m Digital Elevation Models, Using GIS/CRWR-Pre. Pro

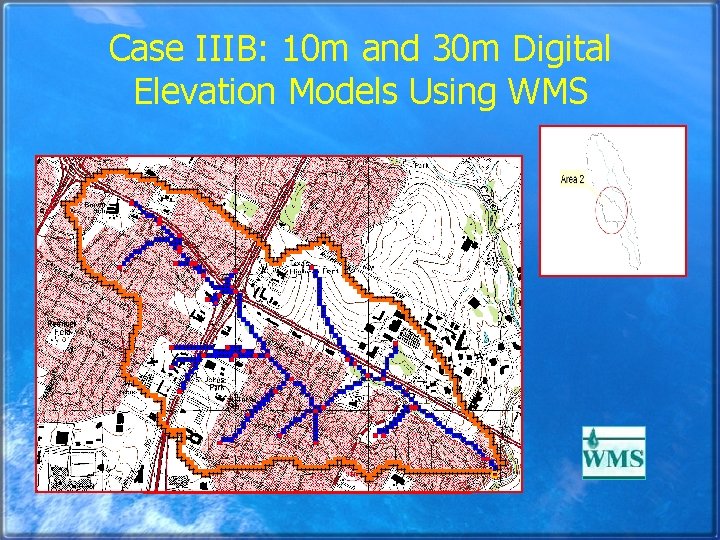
Case IIIB: 10 m and 30 m Digital Elevation Models Using WMS

Case IV: Automated Methods Using WMS and a Triangulated Irregular Network Model (TIN)

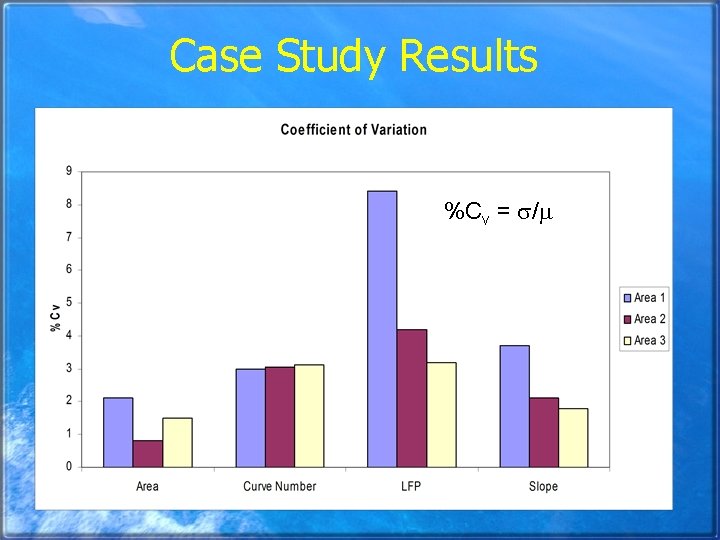
Case Study Results %Cv = /

Outline § Flood discharge calculation overview § Problem statement and research objectives § Case studies § Sensitivity analysis of hydrologic parameters § Conclusions

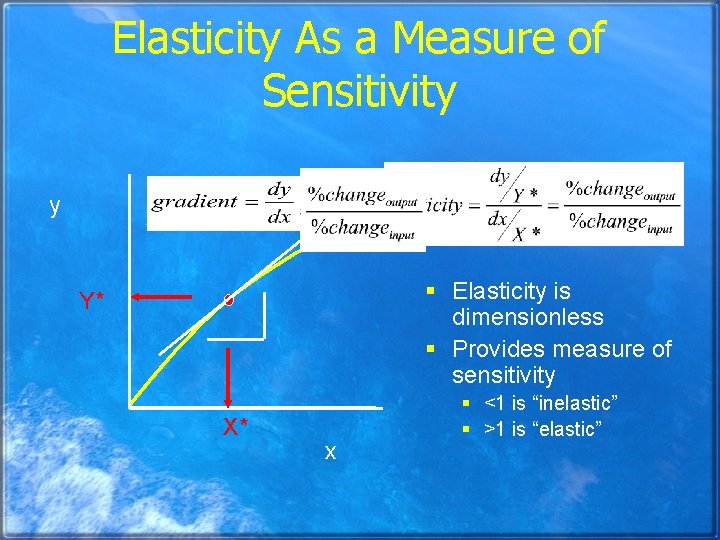
Elasticity As a Measure of Sensitivity y § Elasticity is dimensionless § Provides measure of sensitivity Y* X* x § <1 is “inelastic” § >1 is “elastic”

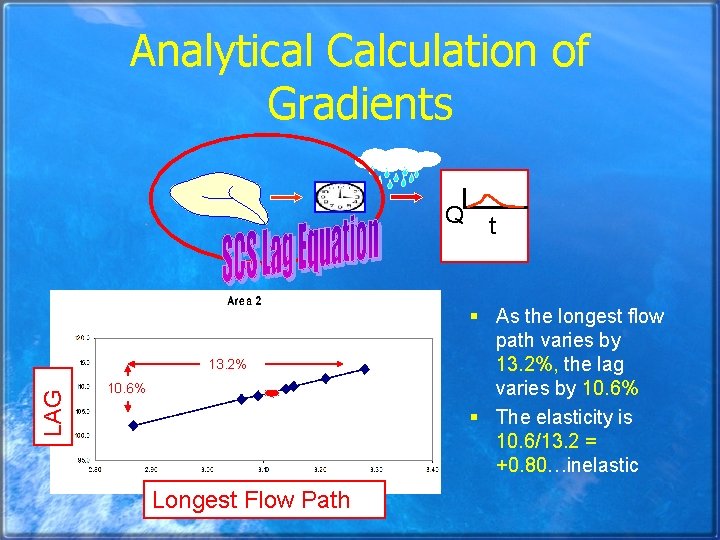
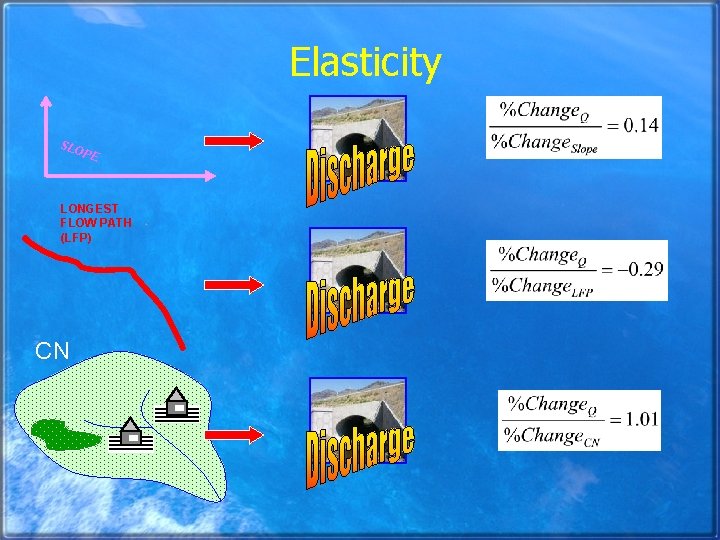
Analytical Calculation of Gradients Q LAG 13. 2% 10. 6% Longest Flow Path t § As the longest flow path varies by 13. 2%, the lag varies by 10. 6% § The elasticity is 10. 6/13. 2 = +0. 80…inelastic

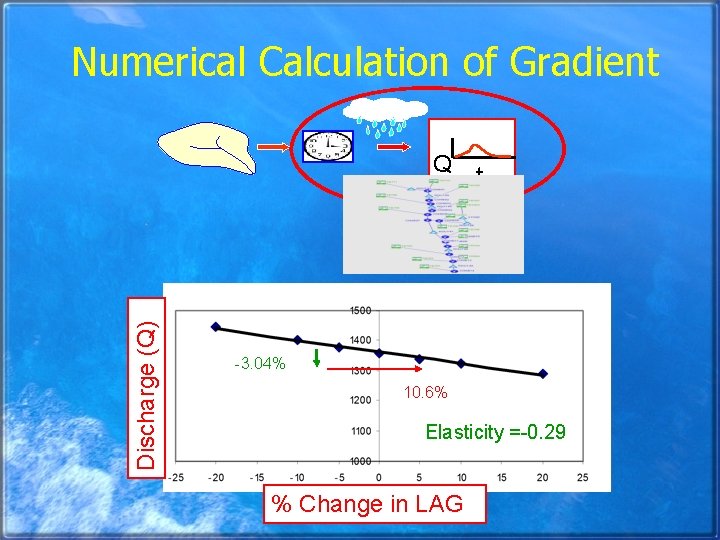
Numerical Calculation of Gradient Discharge (Q) Q t -3. 04% 10. 6% Elasticity =-0. 29 % Change in LAG

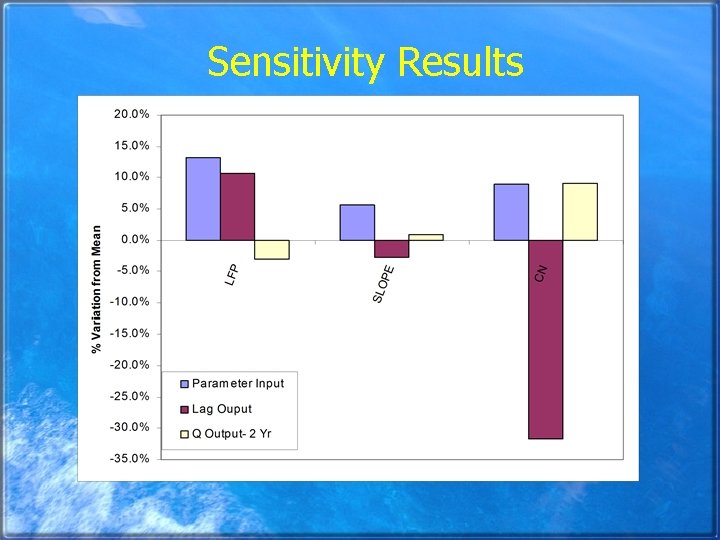
Sensitivity Results % change in parameter…. . % change in lag…. . % change in Q

Elasticity SLO PE LONGEST FLOW PATH (LFP) CN

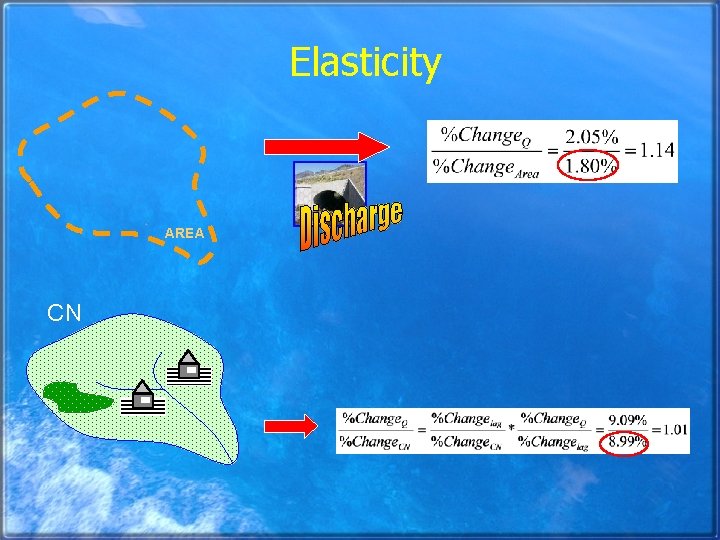
Elasticity AREA CN

Conclusions § Automated methods using grid-based DEMs are less time consuming than traditional methods…USE AUTOMATED METHODS § Slope and longest flow path measurements do not greatly influence discharge § Measurements of area do not vary greatly, spend time/resources obtaining accurate soil and land use data for CN

~Thanks ~ Dr. Maidment David Stolpa Dr. Charbeneau Dr. Barrett Dr. Nelson CRWR Group EWRE Friends Environmental Modeling Systems, Inc.