Ordinary Differential Equations Topic RungeKutta 4 th Order

  • Slides: 13
Download presentation
Ordinary Differential Equations Topic: Runge-Kutta 4 th Order Method A. P. Othman, Ph. D

Ordinary Differential Equations Topic: Runge-Kutta 4 th Order Method A. P. Othman, Ph. D Pusat Pengajian Fizik Gunaan UKM 12/26/2021 http: //numericalmethods. eng. usf. e du 1

Runge-Kutta 4 th Order Method For Runge Kutta 4 th order method is given

Runge-Kutta 4 th Order Method For Runge Kutta 4 th order method is given by where http: //numericalmethods. eng. usf. e du 2

How to write Ordinary Differential Equation How does one write a first order differential

How to write Ordinary Differential Equation How does one write a first order differential equation in the form of Example is rewritten as In this case http: //numericalmethods. eng. usf. e du 3

Example A ball at 1200 K is allowed to cool down in air at

Example A ball at 1200 K is allowed to cool down in air at an ambient temperature of 300 K. Assuming heat is lost only due to radiation, the differential equation for the temperature of the ball is given by Find the temperature at Assume a step size of seconds using Runge-Kutta 4 th order method. seconds. http: //numericalmethods. eng. usf. e du 4

Solution Step 1: http: //numericalmethods. eng. usf. e du 5

Solution Step 1: http: //numericalmethods. eng. usf. e du 5

Solution Cont is the approximate temperature at http: //numericalmethods. eng. usf. e du 6

Solution Cont is the approximate temperature at http: //numericalmethods. eng. usf. e du 6

Solution Cont Step 2: http: //numericalmethods. eng. usf. e du 7

Solution Cont Step 2: http: //numericalmethods. eng. usf. e du 7

Solution Cont is the approximate temperature at = http: //numericalmethods. eng. usf. e du

Solution Cont is the approximate temperature at = http: //numericalmethods. eng. usf. e du 8

Solution Cont The exact solution of the ordinary differential equation is given by the

Solution Cont The exact solution of the ordinary differential equation is given by the solution of a non-linear equation as The solution to this nonlinear equation at t=480 seconds is http: //numericalmethods. eng. usf. e du 9

Comparison with exact results Figure 1. Comparison of Runge-Kutta 4 th order method with

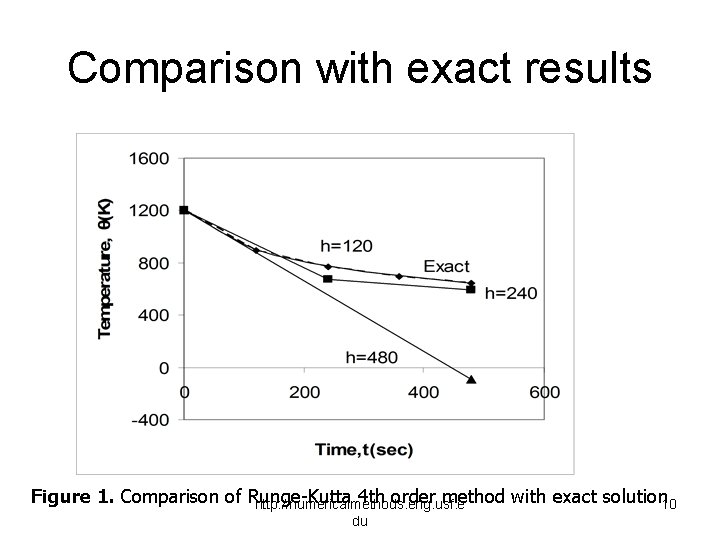
Comparison with exact results Figure 1. Comparison of Runge-Kutta 4 th order method with exact solution 10 http: //numericalmethods. eng. usf. e du

Effect of step size Table 1. Temperature at 480 seconds as a function of

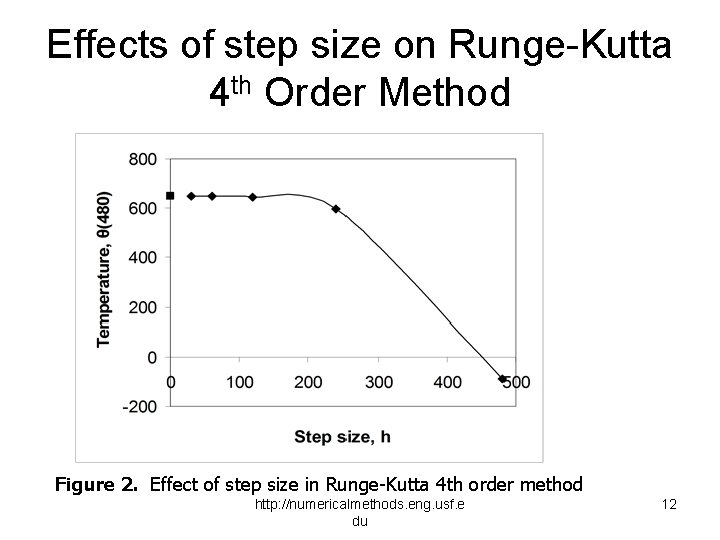
Effect of step size Table 1. Temperature at 480 seconds as a function of step size, h Step 480 240 120 60 30 -90. 278 737. 85 113. 94 594. 91 52. 660 8. 1319 646. 16 1. 4122 0. 21807 647. 54 0. 033626 0. 0051926 647. 57 0. 00086900 0. 00013419 (exact) http: //numericalmethods. eng. usf. e du 11

Effects of step size on Runge-Kutta 4 th Order Method Figure 2. Effect of

Effects of step size on Runge-Kutta 4 th Order Method Figure 2. Effect of step size in Runge-Kutta 4 th order method http: //numericalmethods. eng. usf. e du 12

Comparison of Euler and Runge. Kutta Methods Figure 3. Comparison of http: //numericalmethods. eng.

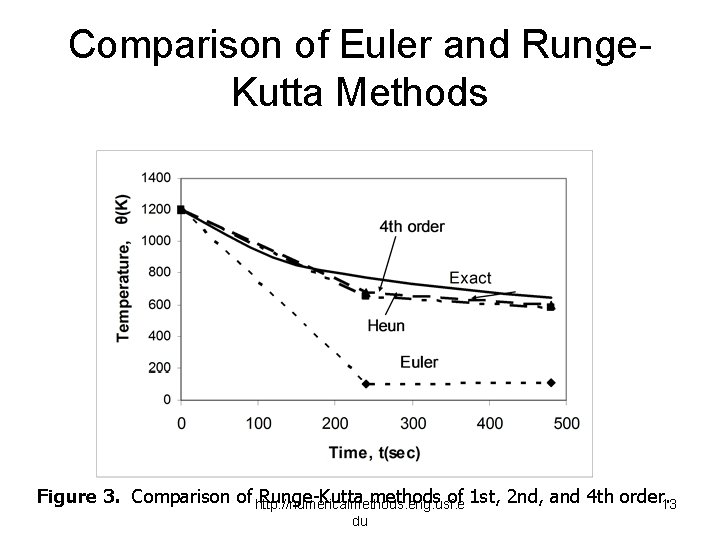
Comparison of Euler and Runge. Kutta Methods Figure 3. Comparison of http: //numericalmethods. eng. usf. e Runge-Kutta methods of 1 st, 2 nd, and 4 th order. 13 du

Differential Equations ordinary differential equations Definition A differentialDifferential Equations ordinary differential equations Definition A differential
RungeKutta 4 th Order Method 1 RungeKutta 4RungeKutta 4 th Order Method 1 RungeKutta 4
Ordinary differential equations II RungeKutta method 2008 AppliedOrdinary differential equations II RungeKutta method 2008 Applied
PART 7 Ordinary Differential Equations ODEs Ordinary DifferentialPART 7 Ordinary Differential Equations ODEs Ordinary Differential
PART 7 Ordinary Differential Equations ODEs Ordinary DifferentialPART 7 Ordinary Differential Equations ODEs Ordinary Differential
Ordinary differential equations ODE An nth order ordinaryOrdinary differential equations ODE An nth order ordinary
Differential Equations Ordinary differential equation ODE Partial differentialDifferential Equations Ordinary differential equation ODE Partial differential
Ordinary Differential Equations and Partial Differential Equations SolutionsOrdinary Differential Equations and Partial Differential Equations Solutions
Ordinary Differential Equations ODEs Differential equations are theOrdinary Differential Equations ODEs Differential equations are the
Differential equations There are ordinary differential equations functionsDifferential equations There are ordinary differential equations functions
Ordinary Differential Equations and Partial Differential Equations SolutionsOrdinary Differential Equations and Partial Differential Equations Solutions
Ordinary Differential Equations ODEs Differential equations are theOrdinary Differential Equations ODEs Differential equations are the