Numerical Methods of Root finding 1 Nonlinear Equations

Numerical Methods of Root finding 1

Nonlinear Equations: Roots – Objective is to find a solution of F(x) = 0 Where F is a polynomial or a transcendental function, given explicitly. – Exact solutions are not possible for most equations. – A number x ± e, ( e > 0 ) is an approximate solution of the equation if there is a solution in the interval [x-e, x+e]. e is the maximum possible error in the approximate solution. – With unlimited resources, it is possible to find an approximate solution with arbitrarily small e. 2

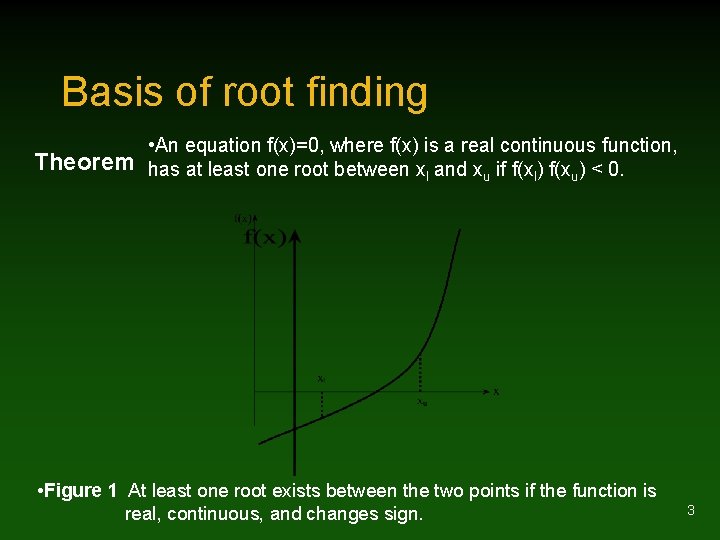
Basis of root finding • An equation f(x)=0, where f(x) is a real continuous function, Theorem has at least one root between xl and xu if f(xl) f(xu) < 0. • Figure 1 At least one root exists between the two points if the function is real, continuous, and changes sign. 3

Bisection Method Let F(x) be a continuous function and let a and b be real numbers such that F(a) and F(b) have opposite signs. Then there is a x* in interval [a, b] such that F(x*) = 0. Then c = (a + b)/2 is an approximate solution with maximum possible error (b – a)/2. If f(c) and f(a) have opposite signs then the solution x* is in the interval [a, c]. Then, again, d = (c + a)/2 is an approximate solution but with max possible error (b – a)/4. Else the solution is in the interval [c, b]. The approximate solution now is (c+b)/2 with max possible error (b-a)/4. Continuing this process n times we can reduce the max possible error to (b-a)/2 n. 4

Algorithm (Bisection Method) 1. Input > 0 , m > 0, x 1 > x 0 so that f(x 0) f(x 1) < 0. Compute f 0 = f(x 0). k = 1 (iteration count) 2. Do { (a) Compute f 2 = f(x 2) = (b) If f 2 f 0 < 0 , set x 1= x 2 otherwise set x 0 = f 2 and f 0 = f 2. (c) Set k = k+1. } 3. While |f 2| > and k m set x = x 2 , the root.

False Position Method (Regula Falsi) Instead of bisecting the interval [x 0, x 1], we choose the point where the straight line through the end points meet the xaxis as x 2 and bracket the root with [x 0, x 2] or [x 2, x 1] depending on the sign of f(x 2).

False Position Method y y=f(x) (x 1, f 1) (x 2, f 2) x 0 x 2 (x 0, f 0) Straight line through (x 0, f 0) , (x 1, f 1) : x 1 x

False Position Method (Algorithm) 1. Choose > 0 (tolerance on |f(x)| ) m > 0 (maximum number of iterations ) k = 1 (iteration count) x 0 , x 1 (so that f 0 , f 1 < 0) 2. { a. Compute f 2 = f(x 2) b. If f 0 f 2 < 0 set x 1 = x 2 , f 0 = f 2 c. k = k+1 } 3. While (|f 2| ) and (k m) 4. x = x 2 , the root.

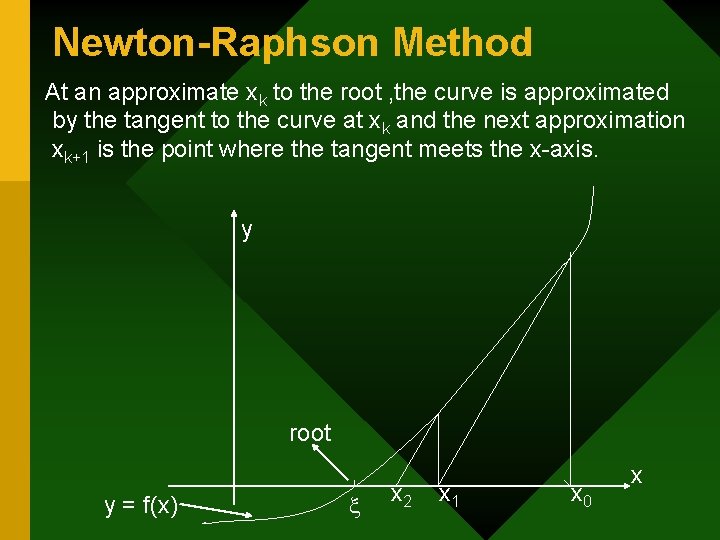
Newton-Raphson Method At an approximate xk to the root , the curve is approximated by the tangent to the curve at xk and the next approximation xk+1 is the point where the tangent meets the x-axis. y root y = f(x) x 2 x 1 x 0 x

Tangent at (xk, fk) : y = f(xk) + f ´(xk)(x-xk) This tangent cuts the x-axis at xk+1 Warning : If f´(xk) is very small , method fails. • Two function Evaluations per iteration

Newton’s Method - Algorithm 1. Choose > 0 (function tolerance |f(x)| < ) m > 0 (Maximum number of iterations) x 0 - initial approximation k - iteration count Compute f(x 0) 2. Do { q = f (x 0) (evaluate derivative at x 0) x 1= x 0 - f 0/q x 0 = x 1 f 0 = f(x 0) k = k+1 } 3. While (|f 0| ) and (k m) 4. x = x 1 the root.

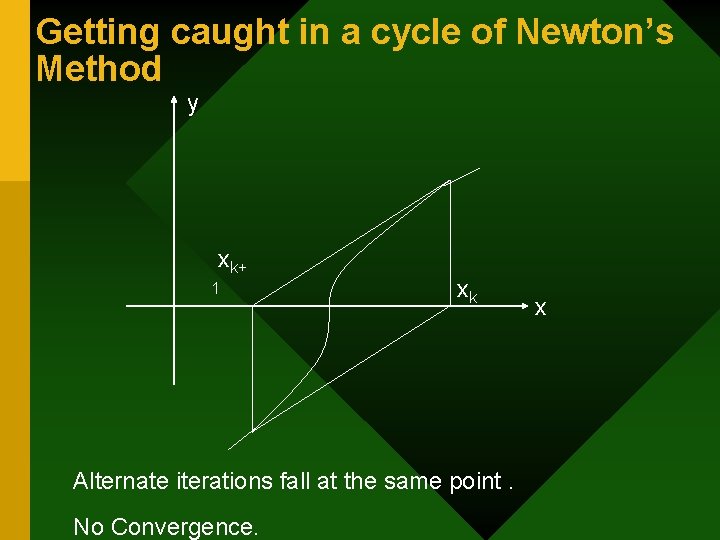
Getting caught in a cycle of Newton’s Method y xk+ 1 xk Alternate iterations fall at the same point. No Convergence. x

Newton’s Method for finding the square root of a number x = a f(x) = x 2 - a 2 = 0 Example : a = 5 , initial approximation x 0 = 2. x 1 = 2. 25 x 2 = 2. 236111111 x 3 = 2. 236067978 x 4 = 2. 236067978

The secant Method • The Newton’s Method requires 2 function evaluations (f, f ). • The Secant Method requires only 1 function evaluation and converges as fast as Newton’s Method at a simple root. • Start with two points x 0, x 1 near the root (no need for bracketing the root as in Bisection Method or Regula Falsi Method). • xk-1 is dropped once xk+1 is obtained.

Secant Method (Geometrical Construction) y y= f(x 1) x 2 x 0 (x 0, f 0) x 1 x (x 1, f 1) • Two initial points x 0, x 1 are chosen • The next approximation x 2 is the point where the straight line joining (x 0, f 0) and (x 1, f 1) meet the x-axis • Take (x 1, x 2) and repeat.

The secant Method (Pseudo Code) 1. Choose > 0 (function tolerance |f(x)| ) m > 0 (Maximum number of iterations) x 0 , x 1 (Two initial points near the root ) f 0 = f(x 0) f 1 = f(x 1) k = 1 (iteration count) 2. Do { x 0 = x 1 f 0 = f 1 x 1= x 2 f 1 = f(x 2) k = k+1 } 3. While (|f 1| ) and (m k)

General remarks on Convergence # The false position method in general converges faster than the bisection method. # The bisection method and the false position method are guaranteed for convergence. # The secant method and the Newton-Raphson method are not guaranteed for convergence.