Root finding Methods Solving NonLinear Equations Root Finding





















































![Muller’s Method 2. The parabola should intersect the three points [xo, f(xo)], [x 1, Muller’s Method 2. The parabola should intersect the three points [xo, f(xo)], [x 1,](https://slidetodoc.com/presentation_image_h/858dc731858224c9c24acf175d00f6a7/image-73.jpg)






- Slides: 80

Root finding Methods Solving Non-Linear Equations (Root Finding)

Root finding Methods • What are root finding methods? • Methods for determining a solution of an equation. • Essentially finding a root of a function, that is, a zero of the function.

Root finding Methods • Where are they used? • Some applications for root finding are: systems of equilibrium, elliptical orbits, the van der Waals equation, and natural frequencies of spring systems.

• The problem of solving non-linear equations or sets of non-linear equations is a common problem in science, applied mathematics.

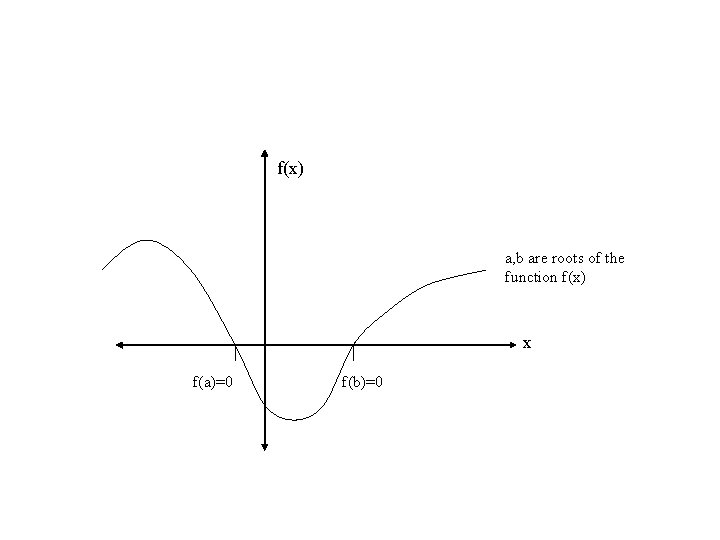
• The problem of solving non-linear equations or sets of non-linear equations is a common problem in science, applied mathematics. • The goal is to solve f(x) = 0 , for the function f(x). • The values of x which make f(x) = 0 are the roots of the equation.

f(x) a, b are roots of the function f(x) x f(a)=0 f(b)=0

• More complicated problems are sets of nonlinear equations. f(x, y, z) = 0 h(x, y, z) = 0 g(x, y, z) = 0

• More complicated problems are sets of nonlinear equations. f(x, y, z) = 0 h(x, y, z) = 0 g(x, y, z) = 0 • For N variables (x, y, z , …), the equations are solvable if there are N linearly independent equations.

• There are many methods for solving non-linear equations. The methods, which will be highlighted have the following properties: 1. the function f(x) is expected to be continuous. If not the method may fail. 2. the use of the algorithm requires that the solution be bounded. 3. once the solution is bounded, it is refined to specified tolerance.

Four such methods are: • Interval Halving (Bisection method) • Regula Falsi (False position) • Secant method • Fixed point iteration • Newton’s method

Bisection Method

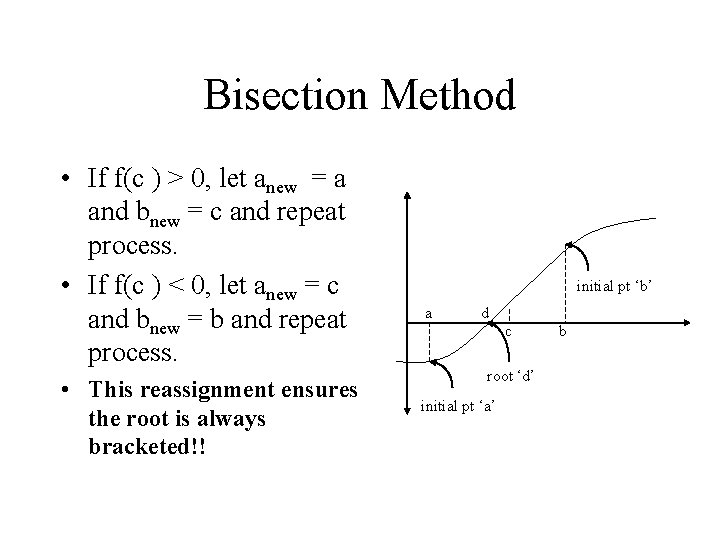
Bisection Method • It is the simplest rootfinding algorithm. • requires previous knowledge of two initial guesses, a and b, so that f(a) and f(b) have opposite signs. initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • Two estimates are chosen so that the solution is bracketed. ie f(a) and f(b) have opposite signs. • In the diagram this f(a) < 0 and f(b) > 0. • The root d lies between a and b! initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • The root d must always be bracketed (be between a and b)! • Iterative method. initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • The interval between a and b is halved by calculating the average of a and b. • The new point c = (a+b)/2. • This produces are two possible intervals: a < x < c and c < x < b. initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • This produces are two possible intervals: a < x < c and c < x < b. • If f(c ) > 0, then x = d must be to the left of c : interval a < x < c. • If f(c ) < 0, then x = d must be to the right of c : interval c < x < b. initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • If f(c ) > 0, let anew = a and bnew = c and repeat process. • If f(c ) < 0, let anew = c and bnew = b and repeat process. • This reassignment ensures the root is always bracketed!! initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method • This produces are two possible intervals: a < x < c and c < x < b. • If f(c ) > 0, then x = d must be to the left of c : interval a < x < c. • If f(c ) < 0, then x = d must be to the right of c : interval c < x < b. initial pt ‘b’ a d c root ‘d’ initial pt ‘a’ b

Bisection Method ci = (ai + bi )/2 if f(ci) > 0; ai+1 = a and bi+1 = c if f(ci) < 0; ai+1 = c and bi+1 = b

Bisection Method • Bisection is an iterative process, where the initial interval is halved until the size of the interval decreases until it is below some predefined tolerance : |a-b| or f(x) falls below a tolerance : |f(c ) – f(c-1)| .

Bisection Method • Advantages 1. Is guaranteed to work if f(x) is continuous and the root is bracketed. 2. The number of iterations to get the root to specified tolerance is known in advance

Bisection Method • Disadvantages 1. Slow convergence. 2. Not applicable when here are multiple roots. Will only find one root at a time.

Linear Interpolation Methods

Linear Interpolation Methods • Most functions can be approximated by a straight line over a small interval. The two methods : - secant and false position are based on this.

Secant Method

Secant Method

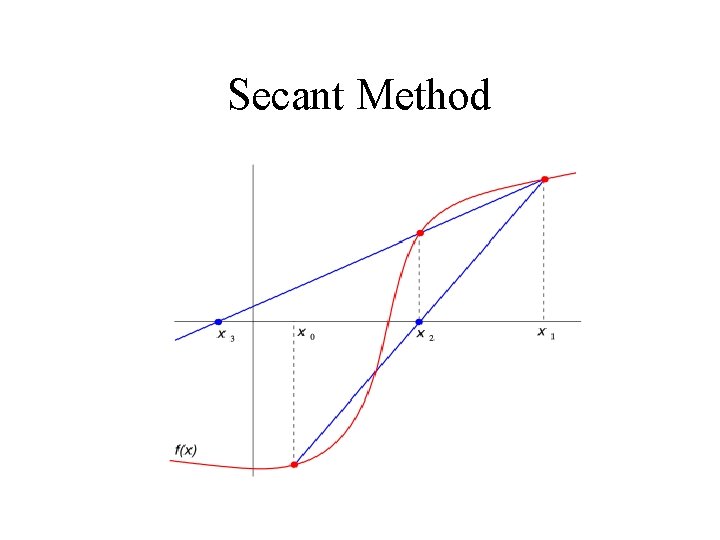
Overview of Secant Method • Again to initial guesses are chosen. • However there is not requirement that the root is bracketed! • The method proceeds by drawing a line through the points to get a new point closer to the root. • This is repeated until the root is found.

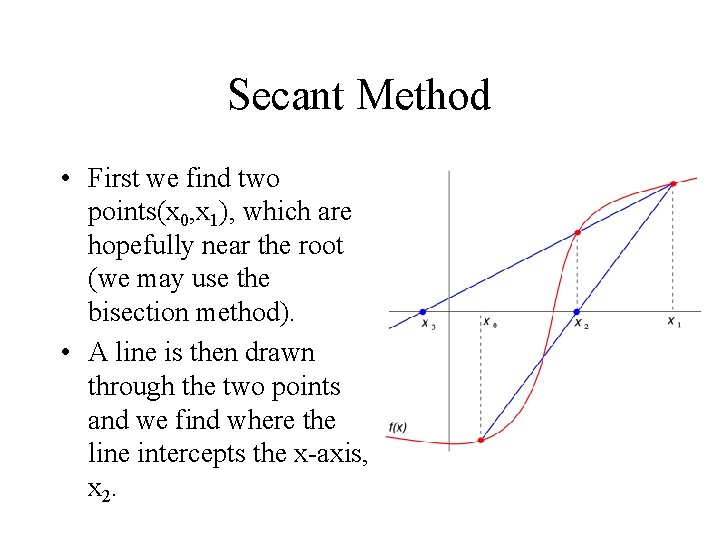
Secant Method • First we find two points(x 0, x 1), which are hopefully near the root (we may use the bisection method). • A line is then drawn through the two points and we find where the line intercepts the x-axis, x 2.

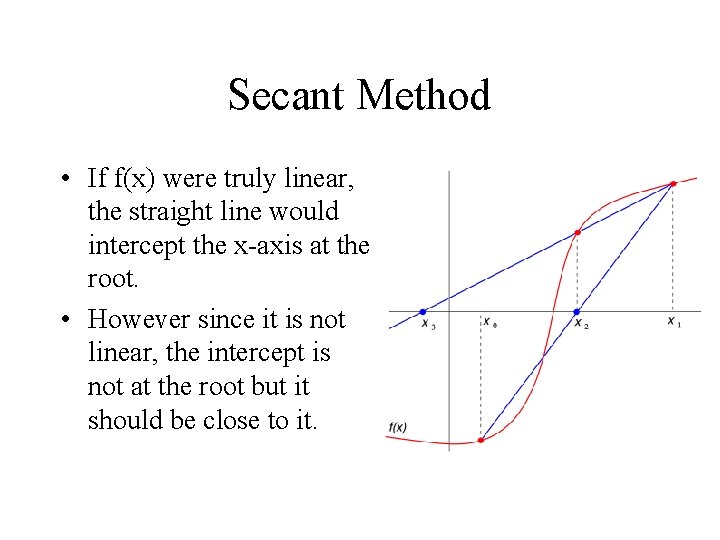
Secant Method • If f(x) were truly linear, the straight line would intercept the x-axis at the root. • However since it is not linear, the intercept is not at the root but it should be close to it.

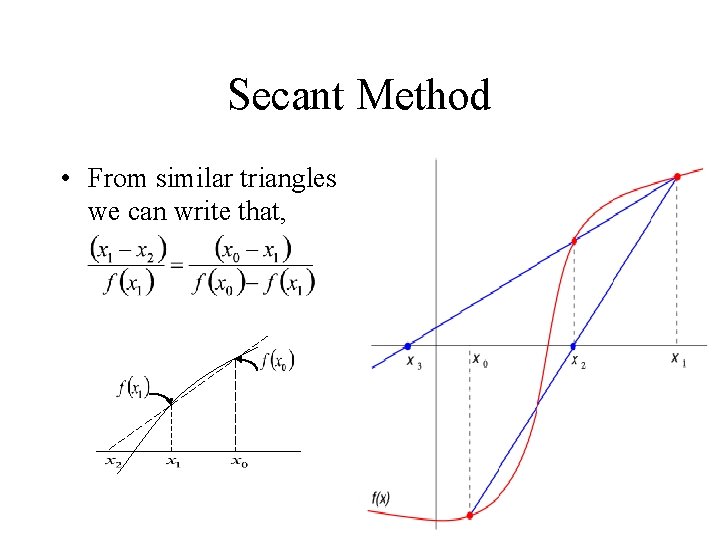
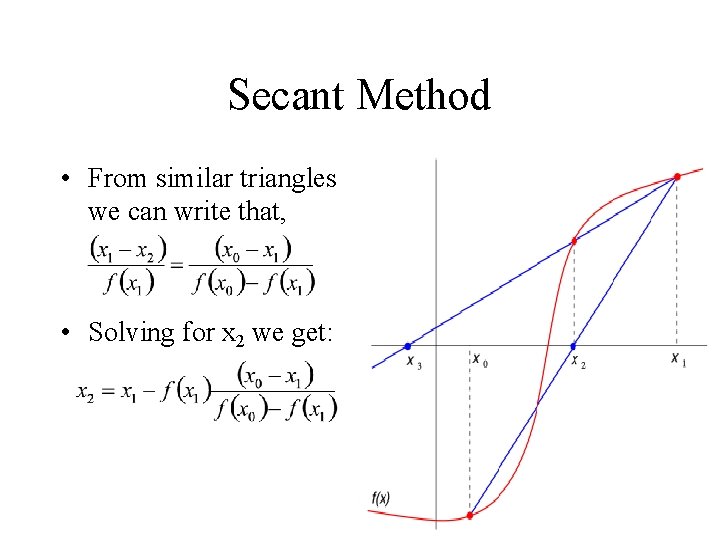
Secant Method • From similar triangles we can write that,

Secant Method • From similar triangles we can write that, • Solving for x 2 we get:

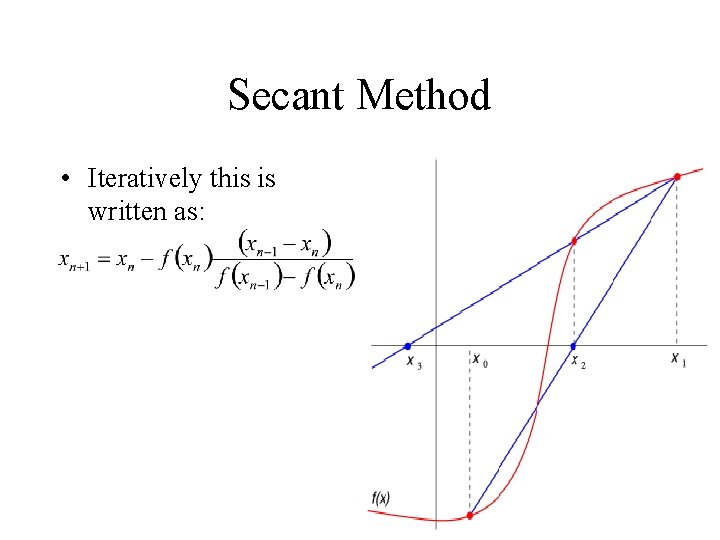
Secant Method • Iteratively this is written as:

Algorithm • • Given two guesses x 0, x 1 near the root, If then Swap x 0 and x 1. Repeat Set x 0 = x 1 Set x 1 = x 2 Until < tolerance value.

• Because the new point should be closer the root after the 2 nd iteration we usually choose the last two points. • After the first iteration there is only one new point. However x 1 is chosen so that it is closer to root that x 0. • This is not a “hard and fast rule”!

Discussion of Secant Method • The secant method has better convergence than the bisection method( see pg 40 of Applied Numerical Analysis). • Because the root is not bracketed there are pathological cases where the algorithm diverges from the root. • May fail if the function is not continuous.

Pathological Case • See Fig 1. 2 page 40

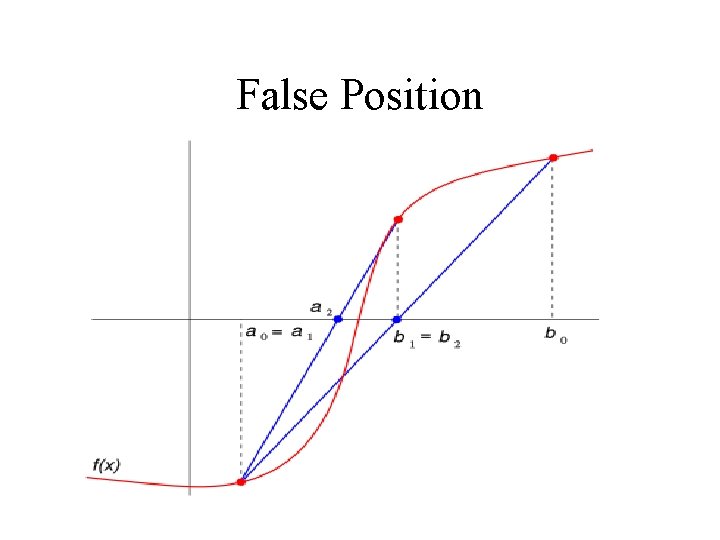
False Position

False Position

False Position • The method of false position is seen as an improvement on the secant method. • The method of false position avoids the problems of the secant method by ensuring that the root is bracketed between the two starting points and remains bracketing between successive pairs.

False Position • This technique is similar to the bisection method except that the next iterate is taken as the line of interception between the pair of x-values and the x-axis rather than at the midpoint.

False Position

Algorithm • Given two guesses x 0, x 1 that bracket the root, • • Repeat Set If is of opposite sign to Set x 1 = x 2 Else Set x 0 = x 1 End If Until < tolerance value. then

Discussion of False Position Method • This method achieves better convergence but a more complicated algorithm. • May fail if the function is not continuous.

Newton’s Method

Newton’s Method • The bisection method is useful up to a point. • In order to get a good accuracy a large number of iterations must be carried out. • A second inadequacy occurs when there are multiple roots to be found.

Newton’s Method • The bisection method is useful up to a point. • In order to get a good accuracy a large number of iterations must be carried out. • A second inadequacy occurs when there are multiple roots to be found. • Newton’s method is a much better algorithm.

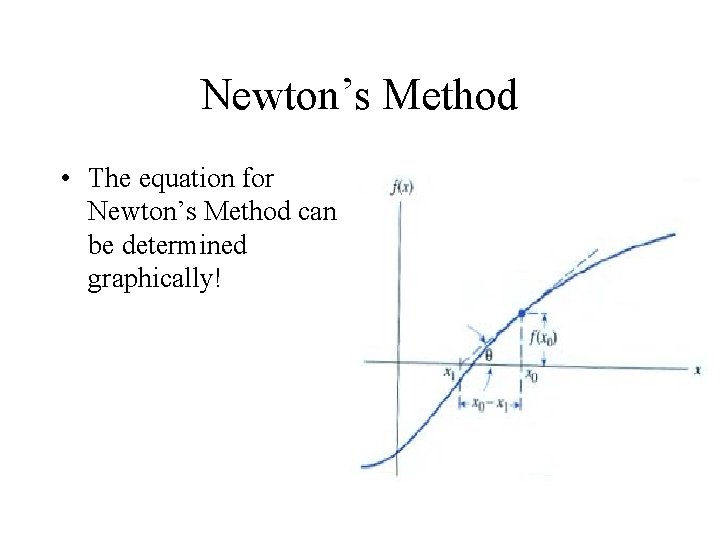
Newton’s Method • Newton’s method relies on calculus and uses linear approximation to the function by finding the tangent to the curve.

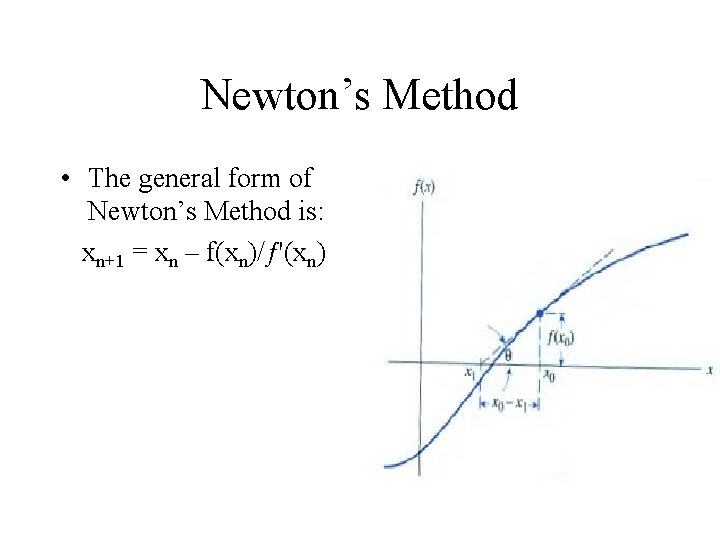
Newton’s Method • Algorithm requires an initial guess, x 0, which is close to the root. • The point where the tangent line to the function (f (x)) meets the x-axis is the next approximation, x 1. • This procedure is repeated until the value of ‘x’ is sufficiently close to zero.

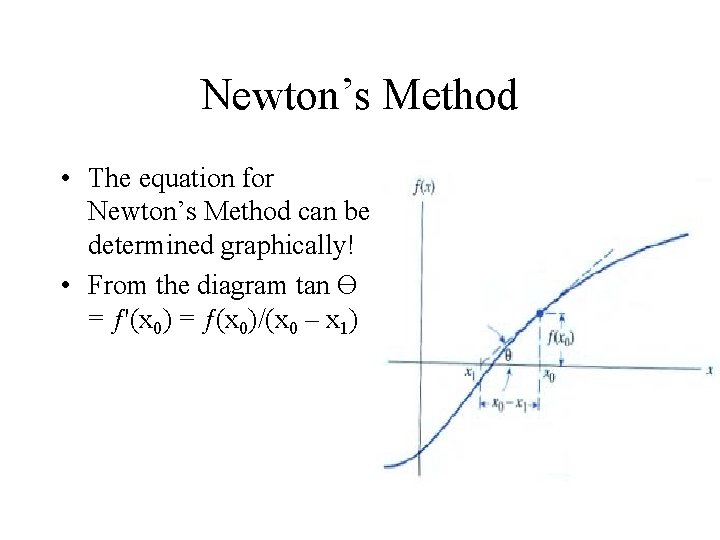
Newton’s Method • The equation for Newton’s Method can be determined graphically!

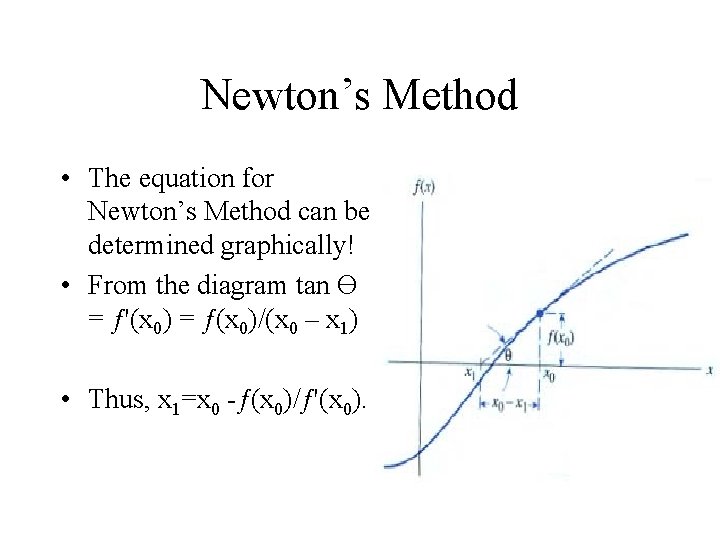
Newton’s Method • The equation for Newton’s Method can be determined graphically! • From the diagram tan Ө = ƒ'(x 0) = ƒ(x 0)/(x 0 – x 1)

Newton’s Method • The equation for Newton’s Method can be determined graphically! • From the diagram tan Ө = ƒ'(x 0) = ƒ(x 0)/(x 0 – x 1) • Thus, x 1=x 0 -ƒ(x 0)/ƒ'(x 0).

Newton’s Method • The general form of Newton’s Method is: xn+1 = xn – f(xn)/ƒ'(xn)

Newton’s Method • The general form of Newton’s Method is: xn+1 = xn – f(xn)/ƒ'(xn) • Algorithm • Pick a starting value for x • Repeat • x: = x – f(x)/ƒ'(x) • Return x

Fixed point iteration

Fixed point iteration

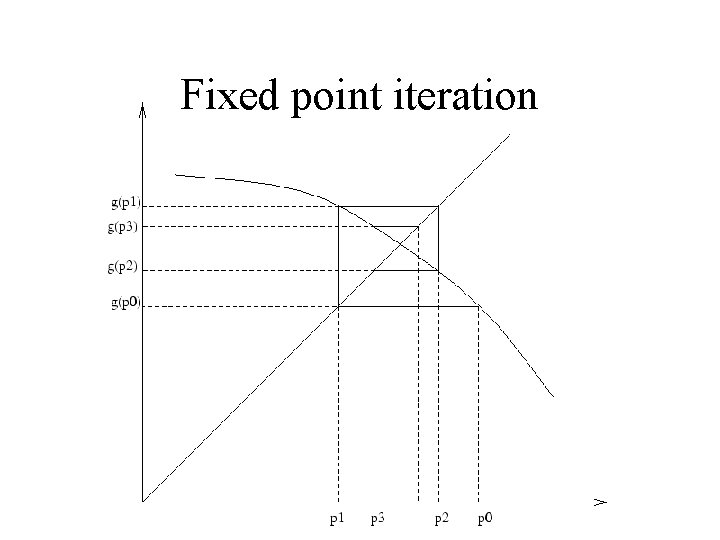
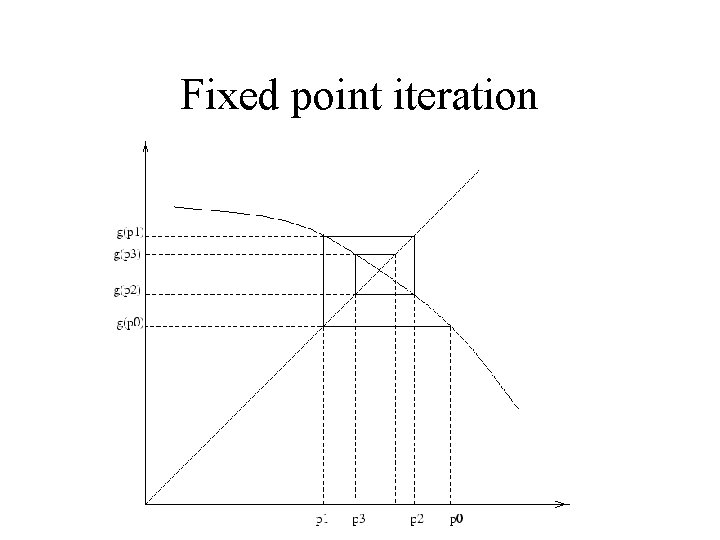
Fixed point iteration • Newton’s method is a special case of the final algorithm: fixed point iteration.

Fixed point iteration • Newton’s method is a special case of the final algorithm: fixed point iteration. • The method relies on the Fixed point Theorem: • If g(x) and g'(x) are continuous on an interval containing a root of the equation g(x) = x, and if |g'(x)| < 1 for all x in the interval then the series xn+1 = g(xn) will converge to the root.

• For Newton’s method g(x) = x – f(x)/ƒ'(x). • However for fixed point, f(x) = 0 thus g(x)=x.

• The fixed point iteration method requires us to rewrite the equation f(x) = 0 in the form x = g(x), then finding x=a such that a = g(a), which is equivalent to f(a) = 0. • The value of x such that x = g(x) is called a fixed point of g(x). • Fixed point iteration essentially solves two functions simultaneously: x(x) and g(x). • The point of intersection of these two functions is the solution to x = g(x), and thus to f(x) = 0.

Fixed point iteration • Consider the example on page 54.

Fixed point iteration

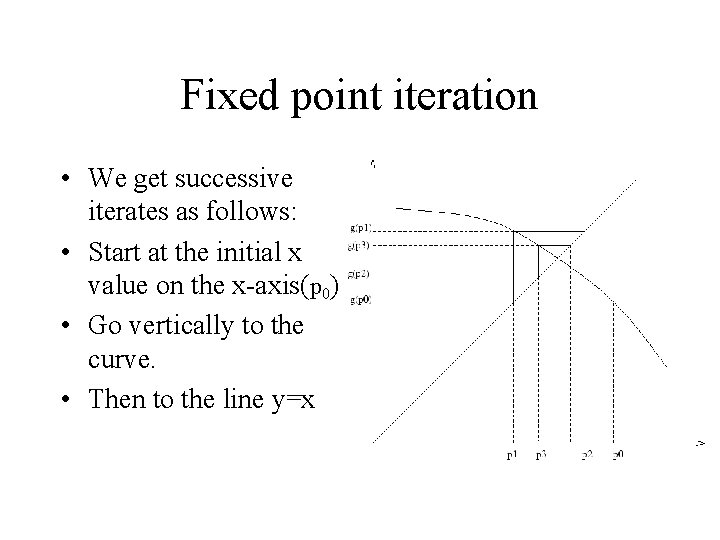
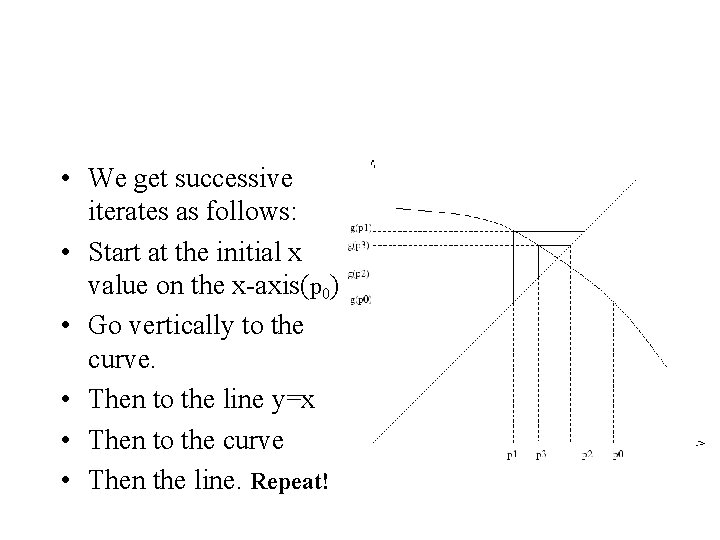
Fixed point iteration • We get successive iterates as follows: • Start at the initial x value on the x-axis(p 0) • Go vertically to the curve. • Then to the line y=x

• We get successive iterates as follows: • Start at the initial x value on the x-axis(p 0) • Go vertically to the curve. • Then to the line y=x • Then to the curve • Then the line. Repeat!

Fixed point iteration • Algorithm • Pick a starting value for x. • Repeat • x : = g(x) • Return x

Fixed point iteration • The procedure starts from an initial guess of x, which is improved by iteration until convergence is achieved. • For convergence to occur, the derivative (dg/dx) must be smaller than 1 in magnitude for the x values that are encountered during the iterations.

Fixed point iteration • Convergence is established by requiring that the change in x from one iteration to the next be no greater in magnitude than some small quantity ε.

Fixed point iteration • Alternative algorithm:

Roots of Polynomials • The roots of polynomials such as • Follow these rules: 1. For an nth order equation, there are n real or complex roots. 2. If n is odd, there is at least one real root. 3. If complex root exist in conjugate pairs (that is, (l+mi and l-mi ), where.

Conventional Methods • The efficiency of bracketing and open methods depends on whether the problem being solved involves complex roots. If only real roots exist, these methods could be used. • Finding good initial guesses complicates both the open and bracketing methods, also the open methods could be susceptible to divergence.

Conventional Methods Special methods have been developed to find the real and complex roots of polynomials: - Müller method - Bairstow methods

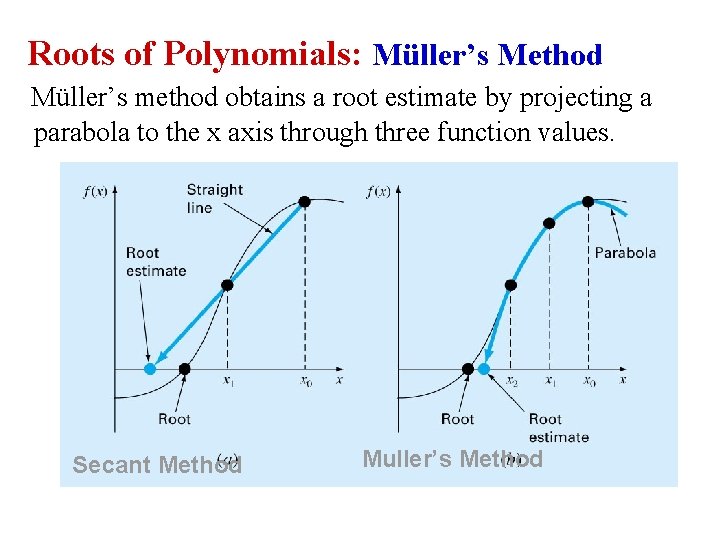
Roots of Polynomials: Müller’s Method Müller’s method obtains a root estimate by projecting a parabola to the x axis through three function values. Secant Method Muller’s Method

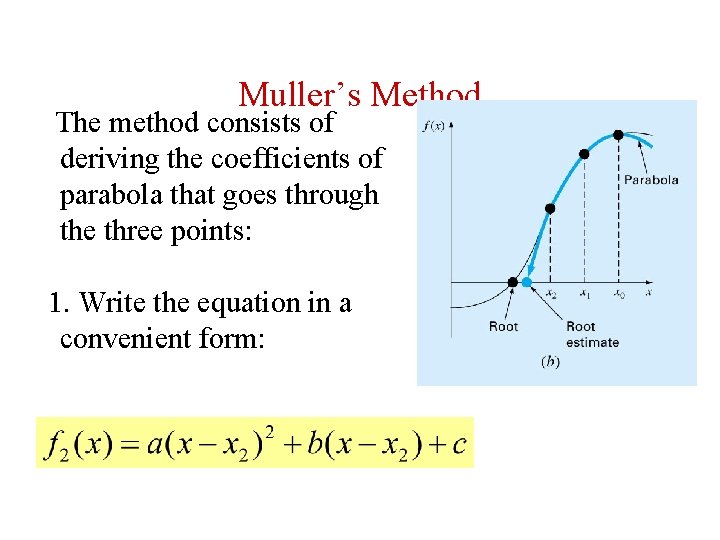
Muller’s Method The method consists of deriving the coefficients of parabola that goes through the three points: 1. Write the equation in a convenient form:
![Mullers Method 2 The parabola should intersect the three points xo fxo x 1 Muller’s Method 2. The parabola should intersect the three points [xo, f(xo)], [x 1,](https://slidetodoc.com/presentation_image_h/858dc731858224c9c24acf175d00f6a7/image-73.jpg)
Muller’s Method 2. The parabola should intersect the three points [xo, f(xo)], [x 1, f(x 1)], [x 2, f(x 2)]. The coefficients of the polynomial can be estimated by substituting three points to give

Muller’s Method 3. Three equations can be solved for three unknowns, a, b, c. Since two of the terms in the 3 rd equation are zero, it can be immediately solved for c = f(x 2).

Muller’s Method Solving the above equations

Muller’s Method • Roots can be found by applying an alternative form of quadratic formula: • The error can be calculated as • ± term yields two roots. This will result in a largest denominator, and will give root estimate that is closest to x 2.

• Once x 3 is determined, the process is repeated using the following guidelines: 1. If only real roots are being located, choose the two original points that are nearest the new root estimate, x 3. 2. If both real and complex roots are estimated, employ a sequential approach just like in secant method, x 1, x 2, and x 3 to replace xo, x 1, and x 2. by Lale Yurttas, Texas A&M University Chapter 7 77

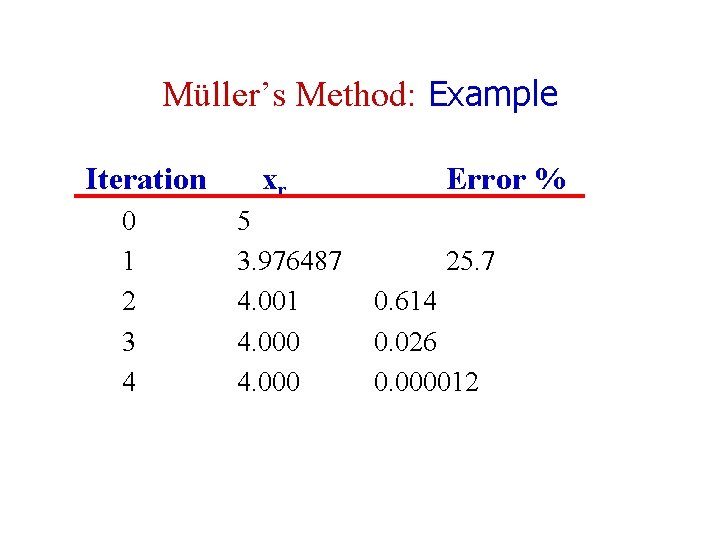
Muller’s Method: Example Use Muller’s method to find roots of f(x)= x 3 - 13 x - 12 Initial guesses of x 0, x 1, and x 2 of 4. 5, 5. 5 and 5. 0 respectively. (Roots are -3, -1 and 4) Solution - f(xo)= f(4. 5)=20. 626, - f(x 1)= f(5. 5)=82. 875 and, - f(x 2)= f(5)= 48. 0 - ho= 5. 5 -4. 5 = 1, h 1 = 5 -5. 5 = -0. 5 - o= (82. 875 -20. 625) /(5. 5 -4. 5) = 62. 25 - 1= (48 -82. 875)/ (5 -5. 5) = 69. 75

Muller’s Method: Example - a = (69. 75 - 62. 25)/(-0. 5+1) = 15 - b =15(-0. 5)+ 69. 75 = 62. 25 - c = 48 ±(b 2 -4 ac)0. 5 = ± 31. 54461 Choose sign similar to the sign of b (+ve) x 3 = 5 + (-2)(48)/(62. 25+31. 54461) = 3. 976487 • The error estimate is t=|(-1. 023513)/(3. 976487)|*100 = 25. 7% • The second iteration will have x 0=5. 5 x 1=5 and x 2=3. 976487

Müller’s Method: Example Iteration 0 1 2 3 4 xr 5 3. 976487 4. 001 4. 000 Error % 25. 7 0. 614 0. 026 0. 000012