Number Systems Number Representation Every number like a

Number Systems

Number Representation Every number like ‘a’ can be represented as

Common Number Systems System Base Symbols Used by humans? Used in computers? Decimal 10 0, 1, … 9 Yes No Binary 2 0, 1 No Yes Octal 8 0, 1, … 7 No No Hexadecimal 16 0, 1, … 9, A, B, … F No No
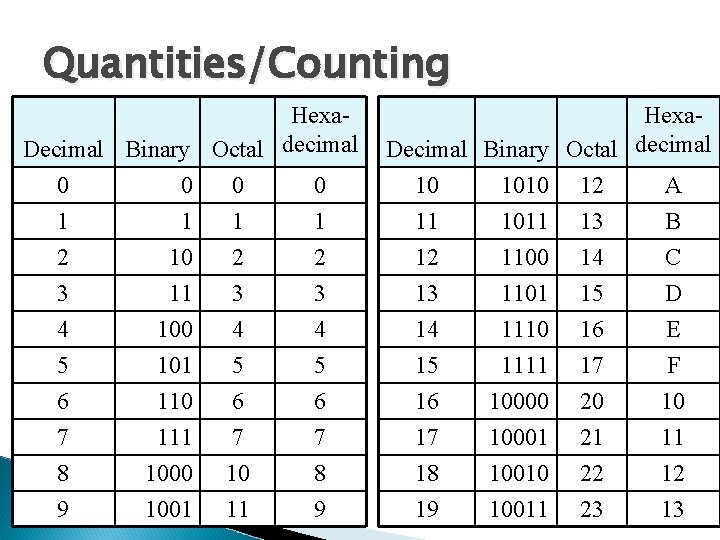
Quantities/Counting Hexa. Decimal Binary Octal decimal 0 0 Hexa. Decimal Binary Octal decimal 10 1010 12 A 1 2 1 10 1 2 11 12 1011 1100 13 14 B C 3 4 5 6 7 8 11 100 101 110 111 1000 3 4 5 6 7 10 3 4 5 6 7 8 13 14 15 16 17 18 1101 1110 1111 10000 10001 10010 15 16 17 20 21 22 D E F 10 11 12 9 1001 11 9 19 10011 23 13
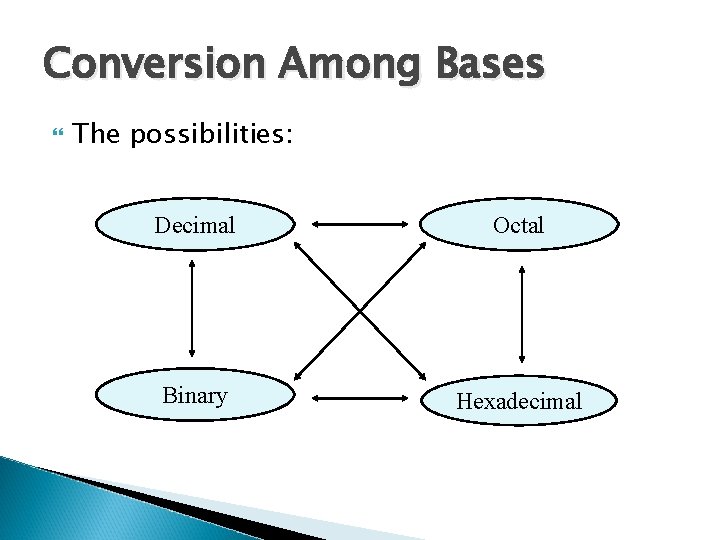
Conversion Among Bases The possibilities: Decimal Octal Binary Hexadecimal

The others to Decimal
Decimal to Decimal (just for fun) Decimal Octal Binary Hexadecimal Next slide…
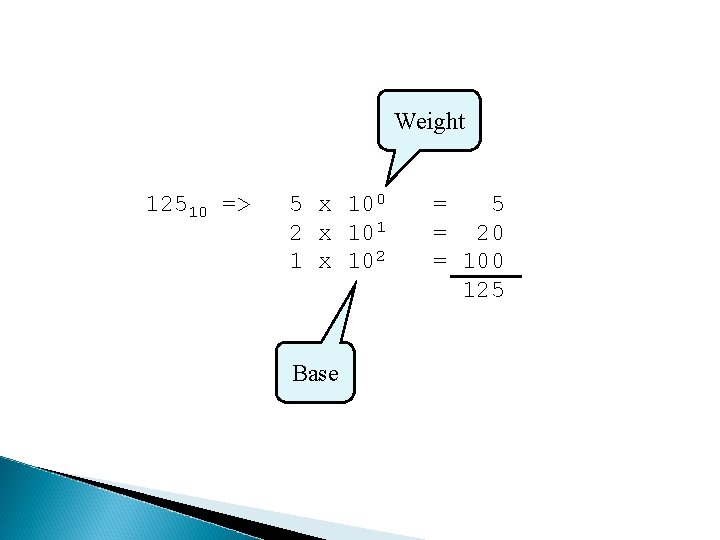
Weight 12510 => 5 x 100 2 x 101 1 x 102 Base = 5 = 20 = 100 125
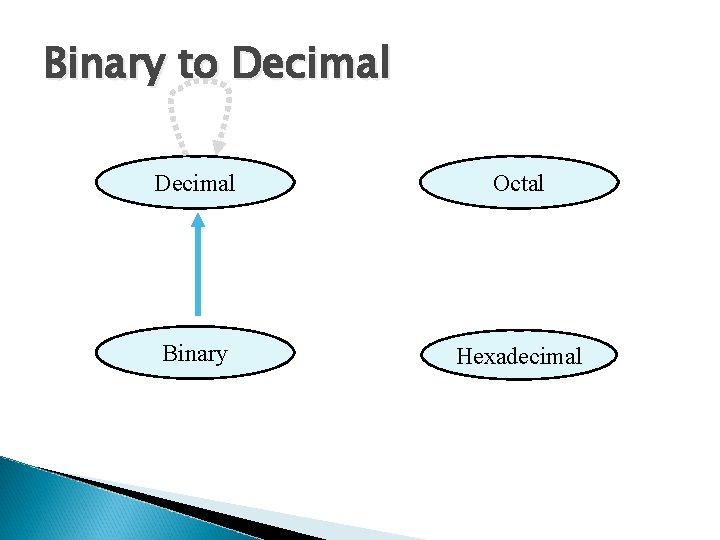
Binary to Decimal Octal Binary Hexadecimal

Binary to Decimal Technique ◦ Multiply each bit by 2 n, where n is the “weight” of the bit ◦ The weight is the position of the bit, starting from 0 on the right ◦ Add the results
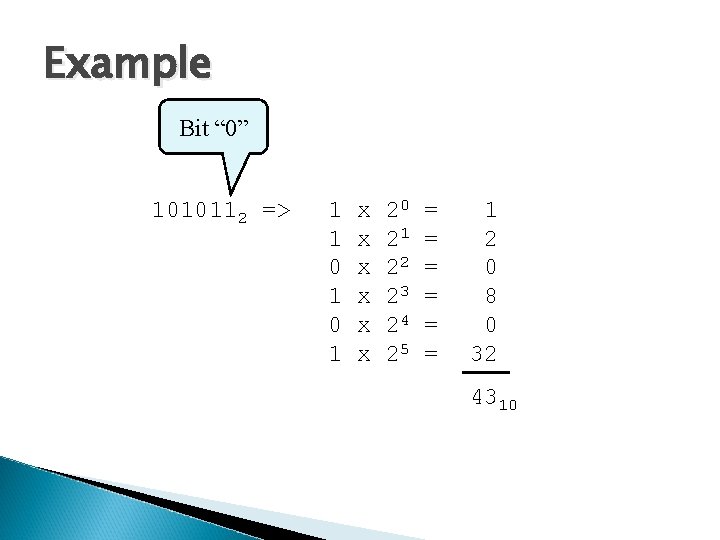
Example Bit “ 0” 1010112 => 1 1 0 1 x x x 20 21 22 23 24 25 = = = 1 2 0 8 0 32 4310
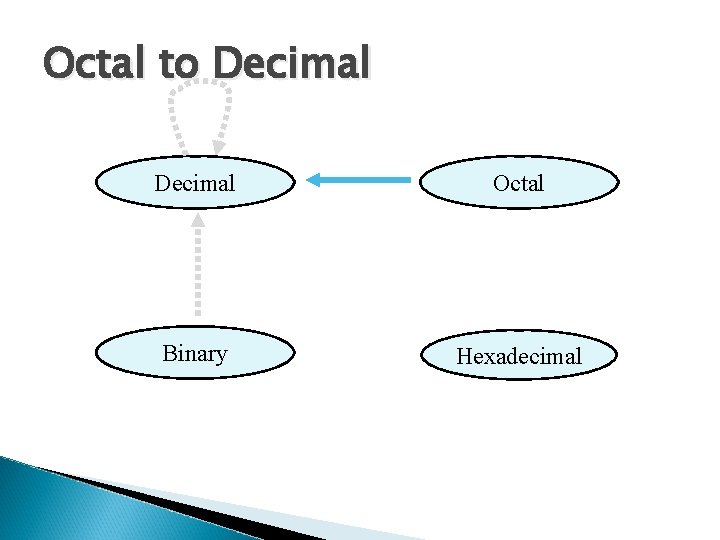
Octal to Decimal Octal Binary Hexadecimal

Octal to Decimal Technique ◦ Multiply each bit by 8 n, where n is the “weight” of the bit ◦ The weight is the position of the bit, starting from 0 on the right ◦ Add the results

Example 7248 => 4 x 80 = 2 x 81 = 7 x 82 = 4 16 448 46810
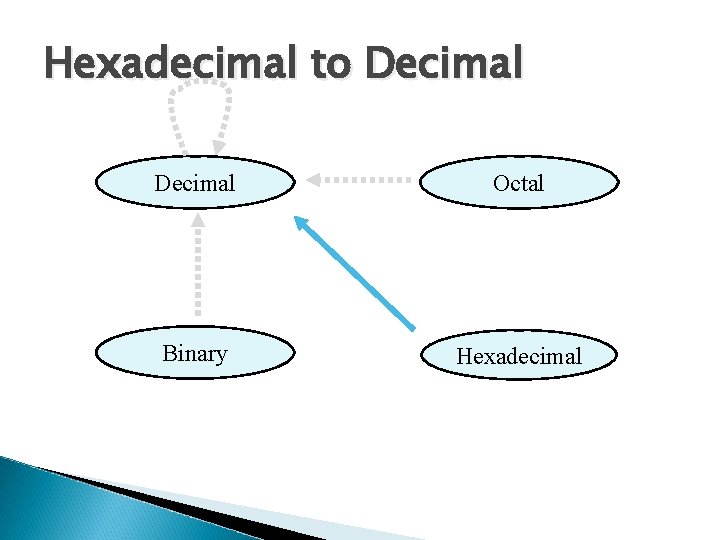
Hexadecimal to Decimal Octal Binary Hexadecimal

Hexadecimal to Decimal Technique ◦ Multiply each bit by 16 n, where n is the “weight” of the bit ◦ The weight is the position of the bit, starting from 0 on the right ◦ Add the results

Example ABC 16 => C x 160 = 12 x 1 = 12 B x 161 = 11 x 16 = 176 A x 162 = 10 x 256 = 2560 274810
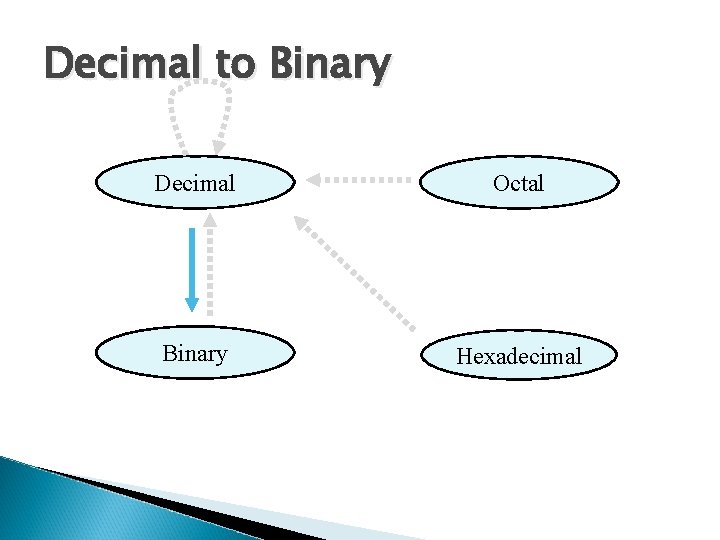
Decimal to Binary Decimal Octal Binary Hexadecimal

Decimal to Binary Technique ◦ ◦ Divide by two, keep track of the remainder First remainder is bit 0 (LSB, least-significant bit) Second remainder is bit 1 Etc.
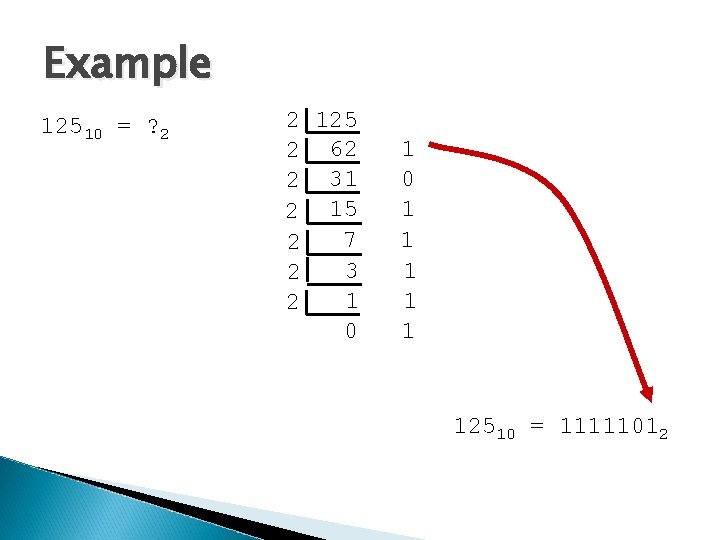
Example 12510 = ? 2 2 125 2 62 2 31 2 15 7 2 3 2 1 2 0 1 1 1 12510 = 11111012
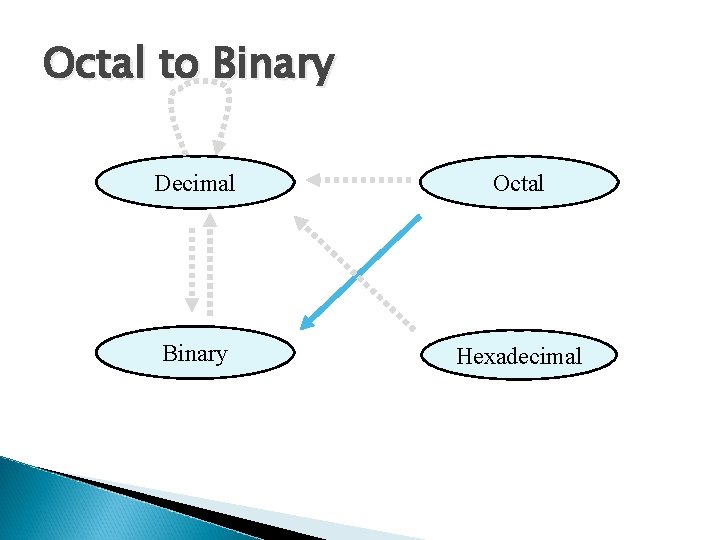
Octal to Binary Decimal Octal Binary Hexadecimal

Octal to Binary Technique ◦ Convert each octal digit to a 3 -bit equivalent binary representation

Example 7058 = ? 2 7 0 5 111 000 101 7058 = 1110001012
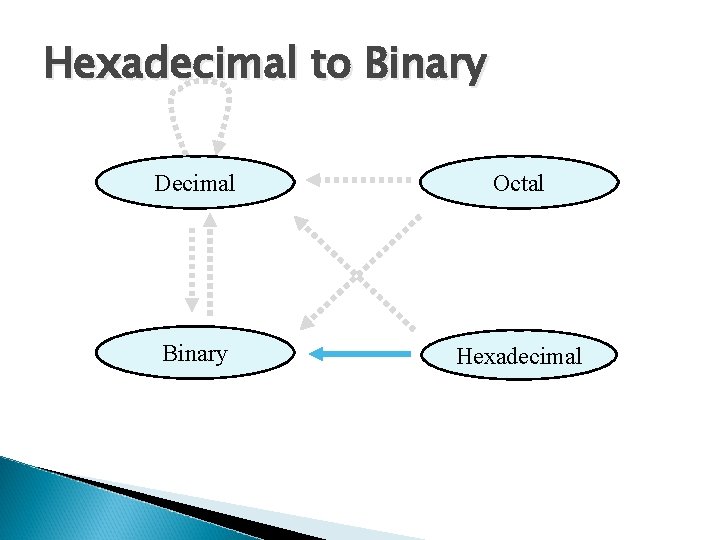
Hexadecimal to Binary Decimal Octal Binary Hexadecimal

Hexadecimal to Binary Technique ◦ Convert each hexadecimal digit to a 4 -bit equivalent binary representation
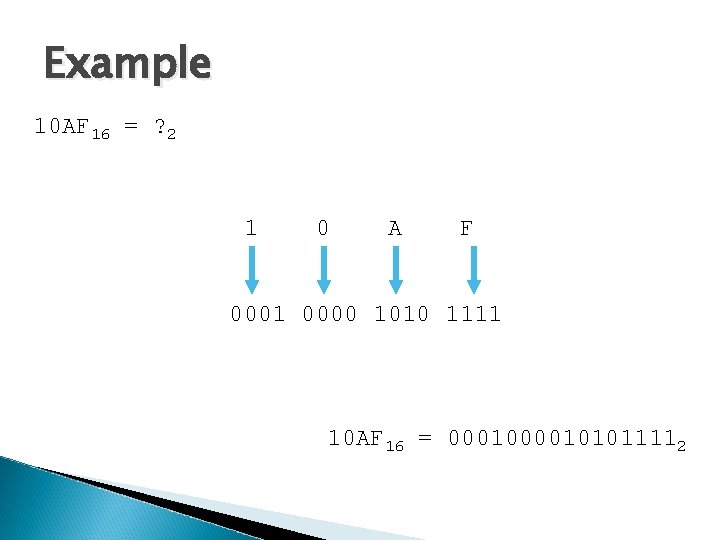
Example 10 AF 16 = ? 2 1 0 A F 0001 0000 1010 1111 10 AF 16 = 000101011112
Decimal to Octal Decimal Octal Binary Hexadecimal

Decimal to Octal Technique ◦ Divide by 8 ◦ Keep track of the remainder
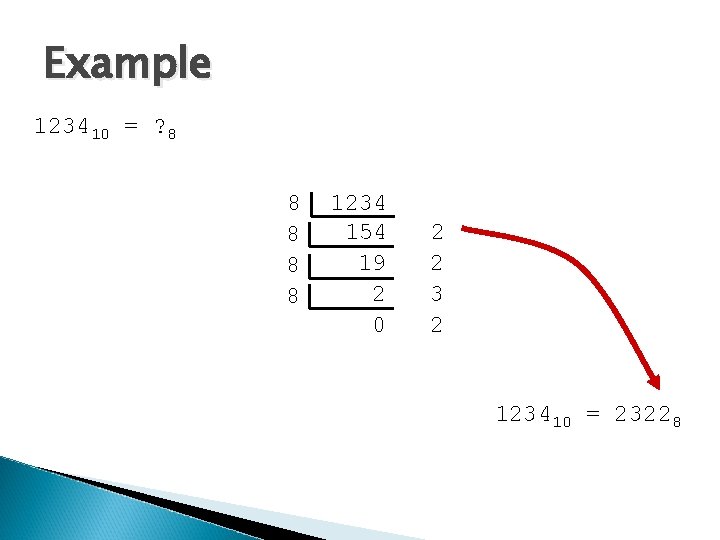
Example 123410 = ? 8 8 8 1234 154 19 2 0 2 2 3 2 123410 = 23228
Decimal to Hexadecimal Decimal Octal Binary Hexadecimal

Decimal to Hexadecimal Technique ◦ Divide by 16 ◦ Keep track of the remainder

Example 123410 = ? 16 16 1234 77 4 0 2 13 = D 4 123410 = 4 D 216
Binary to Octal Decimal Octal Binary Hexadecimal

Binary to Octal Technique ◦ Group bits in threes, starting on right ◦ Convert to octal digits

Example 10110101112 = ? 8 1 010 111 1 3 2 7 10110101112 = 13278
Binary to Hexadecimal Decimal Octal Binary Hexadecimal

Binary to Hexadecimal Technique ◦ Group bits in fours, starting on right ◦ Convert to hexadecimal digits
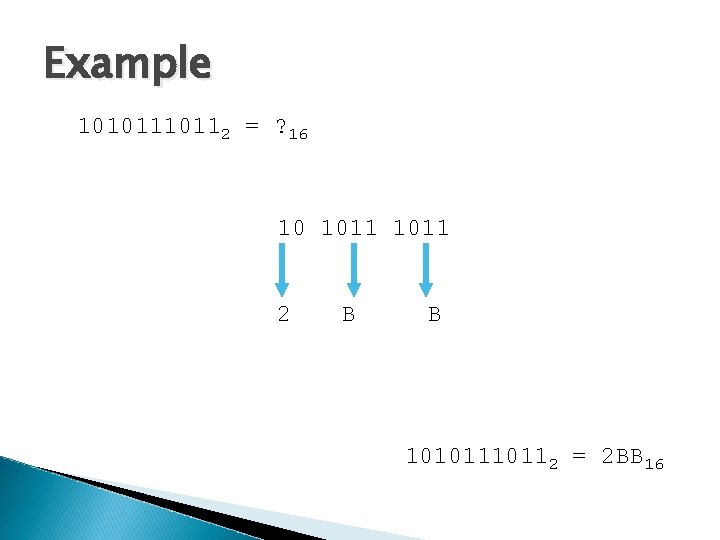
Example 1010112 = ? 16 10 1011 2 B B 1010112 = 2 BB 16
Octal to Hexadecimal Decimal Octal Binary Hexadecimal

Octal to Hexadecimal Technique ◦ Use binary as an intermediary
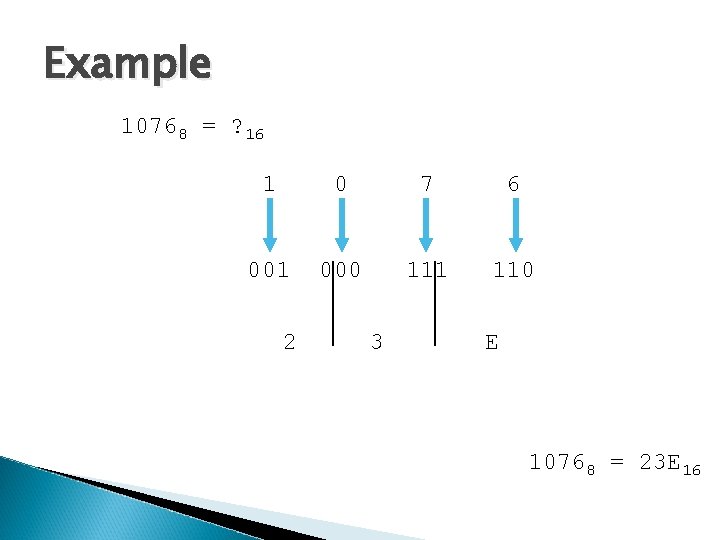
Example 10768 = ? 16 1 0 7 6 001 000 111 110 2 3 E 10768 = 23 E 16
Hexadecimal to Octal Decimal Octal Binary Hexadecimal

Hexadecimal to Octal Technique ◦ Use binary as an intermediary
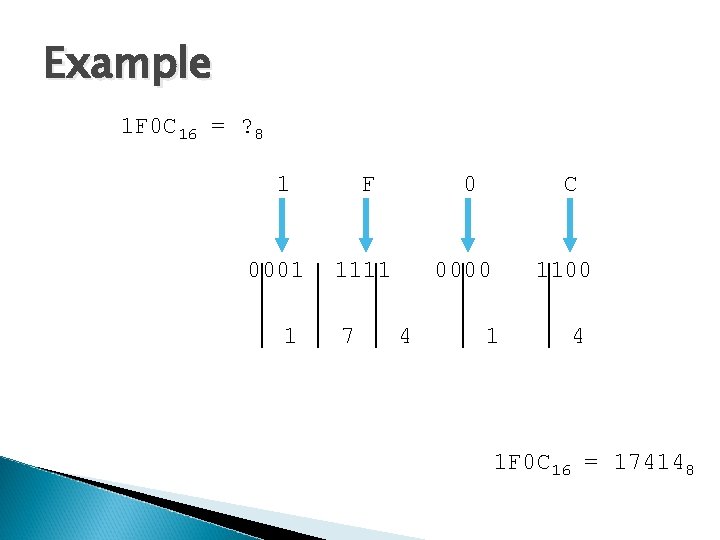
Example 1 F 0 C 16 = ? 8 1 0001 1 F 0 1111 7 C 0000 4 1100 1 4 1 F 0 C 16 = 174148
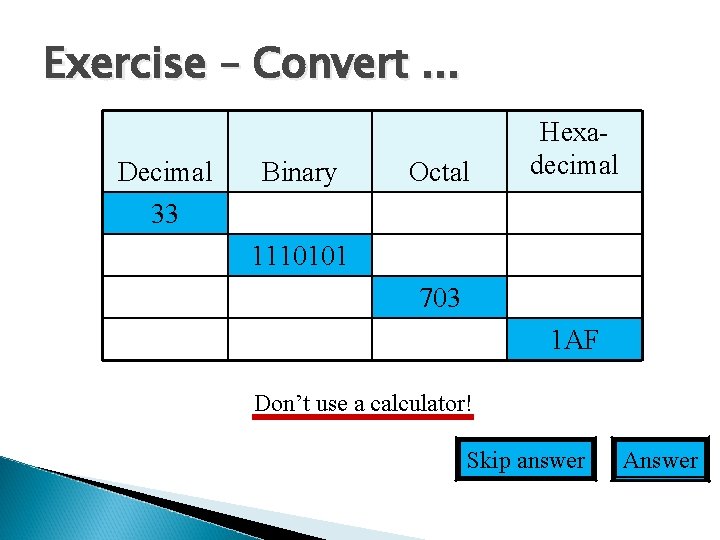
Exercise – Convert. . . Decimal 33 Binary Octal Hexadecimal 1110101 703 1 AF Don’t use a calculator! Skip answer Answer
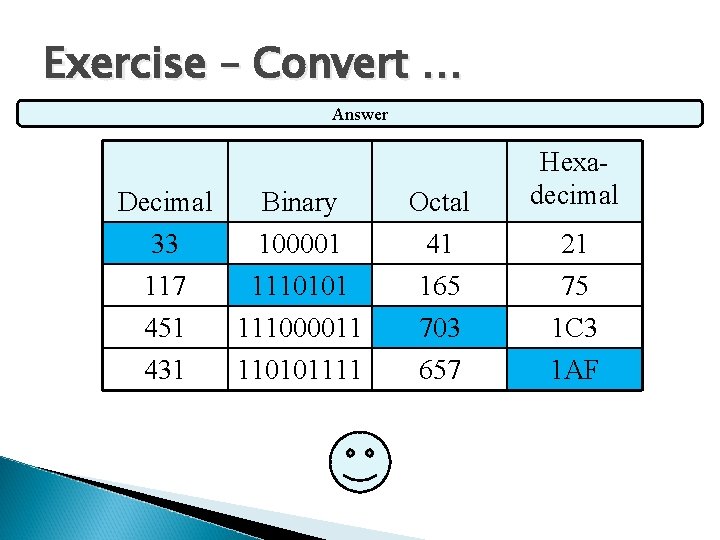
Exercise – Convert … Answer Decimal 33 117 Binary 100001 1110101 Octal 41 165 451 431 111000011 110101111 703 657 Hexadecimal 21 75 1 C 3 1 AF
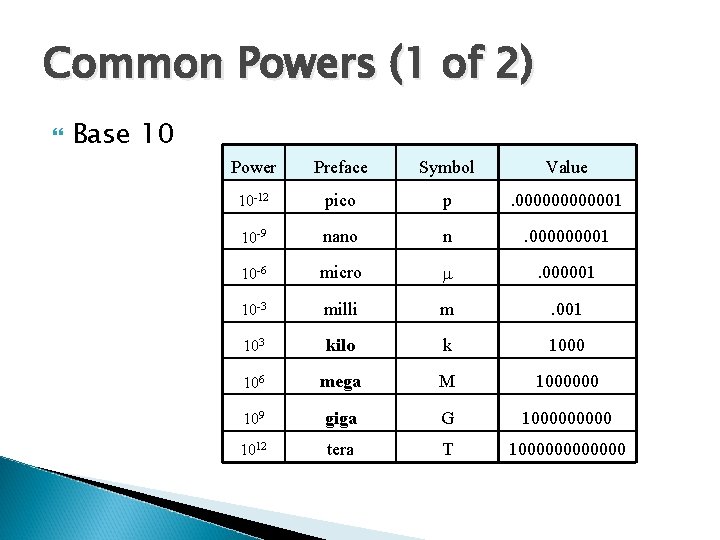
Common Powers (1 of 2) Base 10 Power Preface Symbol Value 10 -12 pico p . 0000001 10 -9 nano n . 00001 10 -6 micro . 000001 10 -3 milli m . 001 103 kilo k 1000 106 mega M 1000000 109 giga G 100000 1012 tera T 1000000
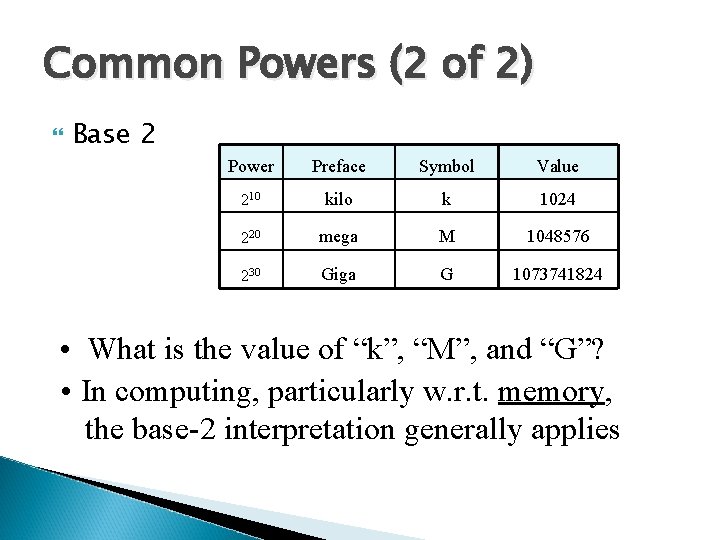
Common Powers (2 of 2) Base 2 Power Preface Symbol Value 210 kilo k 1024 220 mega M 1048576 230 Giga G 1073741824 • What is the value of “k”, “M”, and “G”? • In computing, particularly w. r. t. memory, the base-2 interpretation generally applies
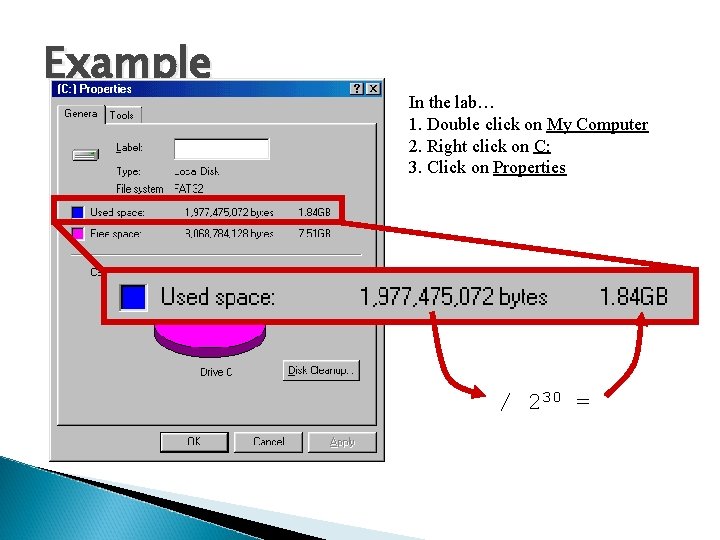
Example In the lab… 1. Double click on My Computer 2. Right click on C: 3. Click on Properties / 230 =

Exercise – Free Space Determine the “free space” on all drives on your personal computer! Free space Drive A: C: D: E: etc. Bytes GB
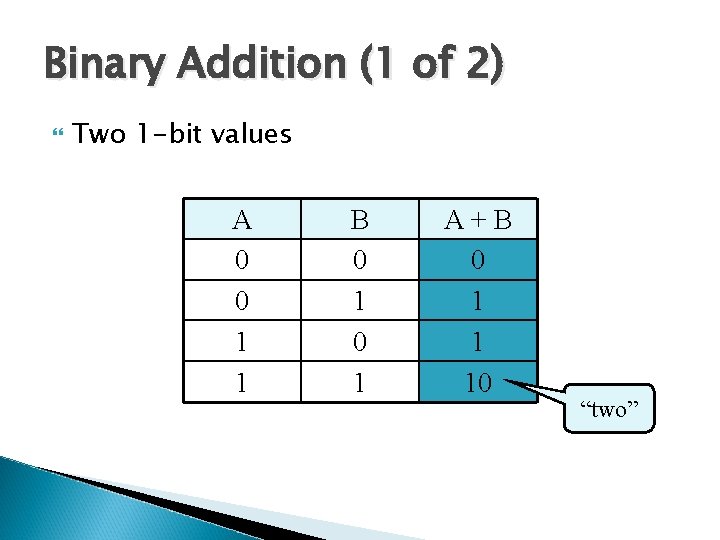
Binary Addition (1 of 2) Two 1 -bit values A 0 0 1 1 B 0 1 A+B 0 1 1 10 “two”

Binary Addition (2 of 2) Two n-bit values ◦ Add individual bits ◦ Propagate carries ◦ E. g. , 1 1 10101 + 11001 101110 21 + 25 46

Multiplication (1 of 3) Decimal (just for fun) 35 x 105 175 000 35 3675

Multiplication (2 of 3) Binary, two 1 -bit values A 0 0 1 1 B 0 1 A B 0 0 0 1

Multiplication (3 of 3) Binary, two n-bit values ◦ As with decimal values ◦ E. g. , 1110 x 1011 1110 0000 1110 10011010 Exercise- Search about binary division?

Fractions Decimal to decimal (just for fun) 3. 14 => 4 x 10 -2 = 0. 04 1 x 10 -1 = 0. 1 3 x 100 = 3 3. 14

Fractions Binary to decimal 10. 1011 => 1 1 0 1 x x x 2 -4 2 -3 2 -2 2 -1 20 21 = = = 0. 0625 0. 125 0. 0 0. 5 0. 0 2. 6875

Fractions Decimal to binary 3. 14579 11. 001001. . 14579 x 2 0. 29158 x 2 0. 58316 x 2 1. 16632 x 2 0. 33264 x 2 0. 66528 x 2 1. 33056 etc.

Exercise – Convert. . . Decimal 29. 8 Binary Octal Hexadecimal 101. 1101 3. 07 C. 82 Don’t use a calculator! Skip answer Answer
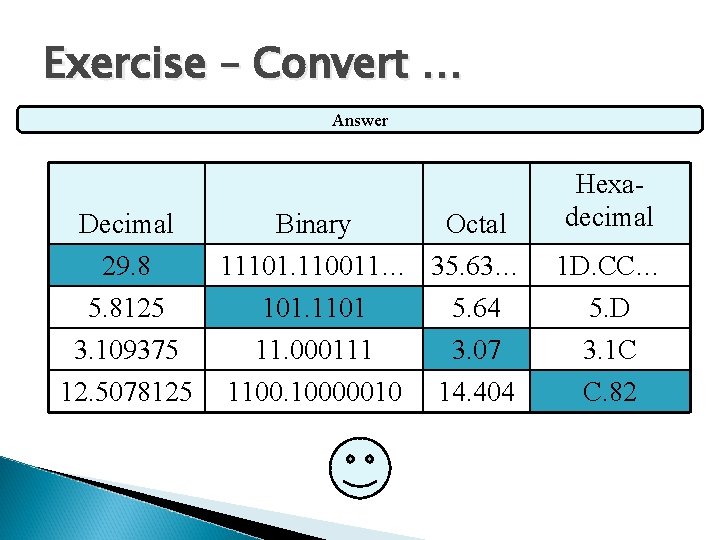
Exercise – Convert … Answer Decimal 29. 8 5. 8125 3. 109375 12. 5078125 Binary Octal 11101. 110011… 35. 63… 101. 1101 5. 64 11. 000111 1100. 10000010 3. 07 14. 404 Hexadecimal 1 D. CC… 5. D 3. 1 C C. 82

Signed Binary number Sign-magnitude 1’s Complement 2’s Complement In all the three methods, the left digit for the positive numbers is zero and for the negative numbers is one!. . Sign bit n - 1

Sign-magnitude The left bit is the sign Positive numbers Negative numbers 0000=+0 1000=-0 0001=+1 1001=-1 0010=+2 1010=-2 0011=+3 1011=-3 0100=+4 1100=-4 0101=+5 1101=-5 0110=+6 1110=-6 0111=+7 1111=-7

Sign-magnitude(cont. ) For a number with n bits: ◦ the biggest number is ◦ the smallest one is We have two values for zero: +0 and -0 Adding two numbers is not easy! 0101+1011? ?

1’s Complement (r-1)’s complement of a (with n digits) is: Positive numbers Negative numbers 0000=+0 1111=-0 0001=+1 1110=-1 0010=+2 1101=-2 0011=+3 1100=-3 0100=+4 1011=-4 0101=+5 1010=-5 0110=+6 1001=-6 0111=+7 1000=-7

1’s Complement to Decimal 1 0 1 1 = +20 + 21 - 23 + 1= - 4

1’s Complement(cont. ) We have two values for zero: +0 and -0 Summation of two numbers: ◦ if a carrier value is generated, add it with the result Exe: What is the biggest and smallest numbers which can be represented by this method?

2’s Complement (r)’s complement of a (with n digits) is: Positive numbers Negative numbers 0000=0 1111=-1 0001=+1 1110=-2 0010=+2 1101=-3 0011=+3 1100=-4 0100=+4 1011=-5 0101=+5 1010=-6 0110=+6 1001=-7 0111=+7 1000=-8
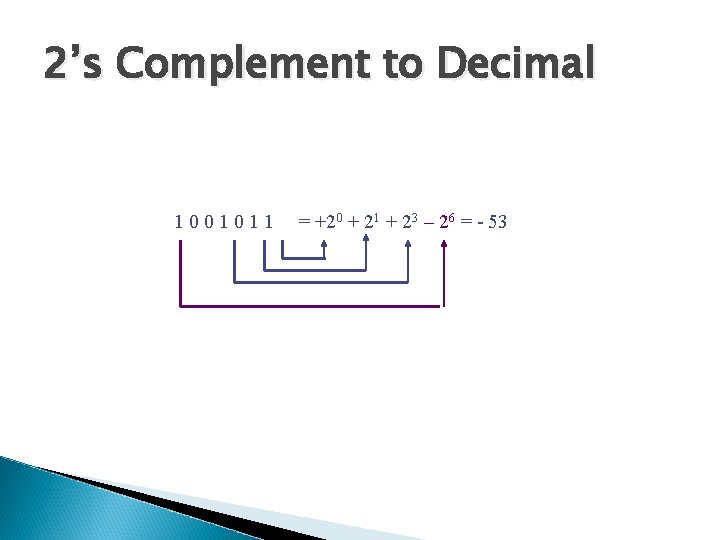
2’s Complement to Decimal 1001011 = +20 + 21 + 23 – 26 = - 53

2’s Complement(cont. ) We have one value for zero

Multiplication (Example 1) Sign extension

Multiplication(Example 2)

Exercise- Search about: How compute the 1’s complement multiplication/summation? How compute 1’s and 2’s complement division?
- Slides: 72