Binary Representation Binary Representation for Numbers Assume 4

Binary Representation

Binary Representation for Numbers � Assume 4 -bit numbers � 5 as an integer 0101 � -5 as an integer How? � 5. 0 as a real number How? What about 5. 5?

Sign Bit �Reserve the most-significant bit to indicate sign �Consider integers in 4 bits Most-significant bit is sign: 0 is positive, 1 is negative The 3 remaining bits is magnitude 0010 = 2 1010 = -2 �How many possible combinations for 4 bits? �How many unique integers using this scheme?

Two’s Complement �Advantages # of combinations of bits = # of unique integers Addition is “natural” �Convert to two’s complement (and vice versa) 1. 2. 3. invert the bits add one ignore the extra carry bit if present �Consider 4 -bit numbers 0010 [2] -> 1101 -> 1110 [-2]

Addition � 0010 [2] + 1110 [-2] 0000 [ignoring the final carry—extra bit] � 0011 [3] + 1110 [-2] 0001 [1] � 1110 [-2] + 1101 [-3] 1011 [-5]

Range of Two’s Complement � 4 -bit numbers Largest positive: 0001 (binary) => 7 (decimal) Smallest negative: 1000 (binary) => -8 (decimal) # of unique integers = # of bit combinations = 16 �n bits ?

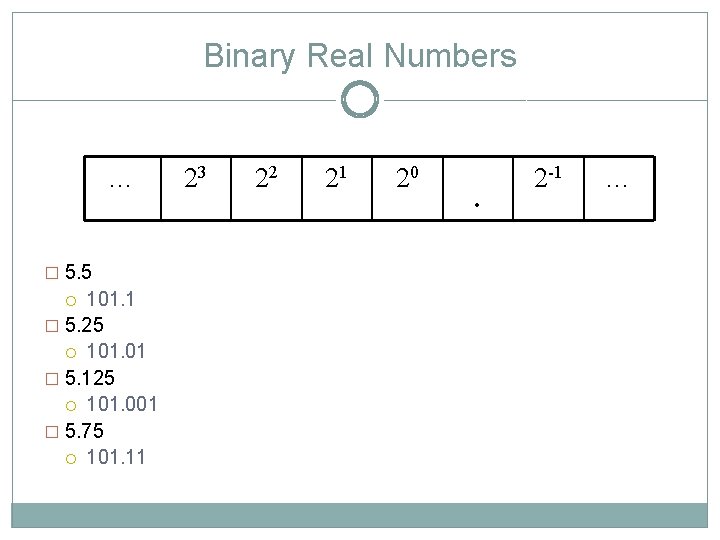
Binary Real Numbers … � 5. 5 101. 1 � 5. 25 101. 01 � 5. 125 101. 001 � 5. 75 101. 11 23 22 21 20 . 2 -1 …

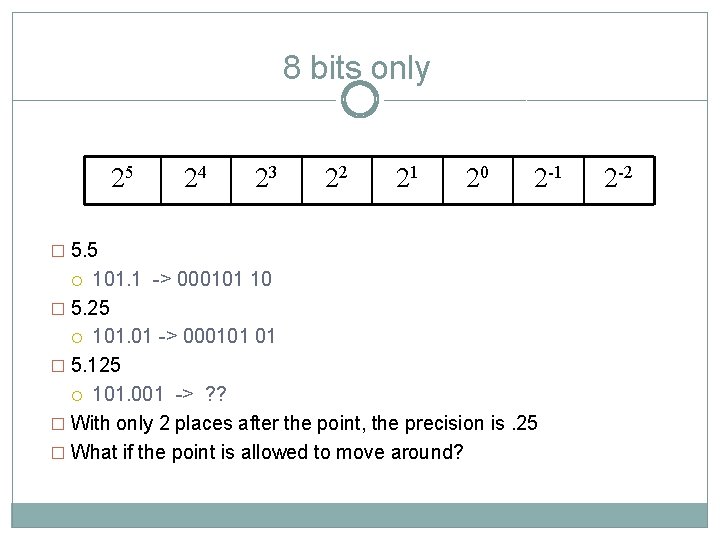
8 bits only 25 24 23 22 21 20 2 -1 � 5. 5 101. 1 -> 000101 10 � 5. 25 101. 01 -> 000101 01 � 5. 125 101. 001 -> ? ? � With only 2 places after the point, the precision is. 25 � What if the point is allowed to move around? 2 -2

Floating-point Numbers � Decimal 54. 3 5. 43 x 101 [scientific notation] � Binary 101. 001 10. 1001 x 21 1. 01001 x 22 [more correctly: 10. 1001 x 101] [more correctly: 1. 01001 x 1010] What can we say about the most significant bit?

Floating-point Numbers �General form: sign 1. mantissa x 2 exponent the most significant digit is right before the dot � Always 1 [no need to represent it] Exponent in Two’s complement � 1. 01001 x 22 Sign: 0 (positive) Mantissa: 0100 Exponent: 010 (decimal 2)

Java Floating-point Numbers sign exponent � Sign: 1 bit [0 is positive] � Mantissa: 23 bits in float 52 bits in double � Exponent: 8 bits in float 11 bits in double mantissa

Imprecision in Floating-Point Numbers �Floating-point numbers often are only approximations since they are stored with a finite number of bits. �Hence 1. 0/3. 0 is slightly less than 1/3. � 1. 0/3. 0 + 1. 0/3. 0 could be less than 1. � www. cs. fit. edu/~pkc/classes/i. Computing/Float. Equality. java

Abstraction Levels �Binary Data � Numbers (unsigned, signed [Two’s complement], floating point) Text (ASCII, Unicode) • HTML Color • Image (JPEG) �Video (MPEG) Sound (MP 3) Instructions � Machine language (CPU-dependent) � Text (ASCII) Assembly language (CPU-dependent) • High-level language (CPU -independent: Java, C++, FORTRAN)