Trees Nature View of a Tree leaves branches

Trees

Nature View of a Tree leaves branches root

Computer Scientist’s View root leaves branches nodes

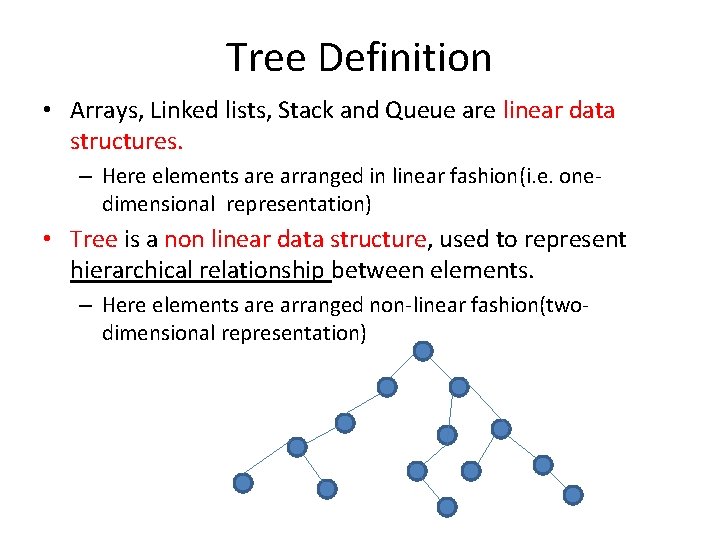
Tree Definition • Arrays, Linked lists, Stack and Queue are linear data structures. – Here elements are arranged in linear fashion(i. e. onedimensional representation) • Tree is a non linear data structure, used to represent hierarchical relationship between elements. – Here elements are arranged non-linear fashion(twodimensional representation)

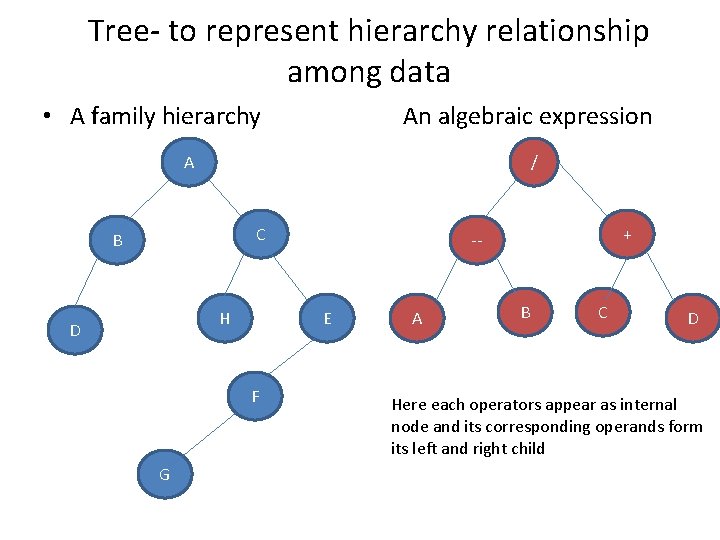
Tree- to represent hierarchy relationship among data • A family hierarchy An algebraic expression A / C B H D E F G + -- A B C D Here each operators appear as internal node and its corresponding operands form its left and right child

Basic terminologies • Node: Main component of any tree structure. It stores the actual data and links to the other node. • Parent: Parent is the immediate predecessor of a node. • Child : Immediate successors of a node are called child. • Root: Specially designated node which has no parent. • Leaf: A node which is at the end and which does not have any child. They are also called terminal node

Basic terminologies • Link: Pointer to a node in the tree. Also called Edge. It is a line drawn from a node N of tree to its successor. • Path: Sequence of consecutive edges. • Level: It is the rank of the hierarchy and the root node is in level 0. • Height: Maximum no. of nodes that is possible in a path starting from root node to a leaf node. It is also called depth. • Degree: Maximum no. of children that is possible for a node is called degree of that node. • Sibling: The nodes which have the same parent

• Leaf nodes are also called external nodes and non leaf nodes are called internal nodes. • If a node is at level l, then its child is at level (l+1) and parent at level( l-1). • Child node at left side is called left child and at right side is called right child.

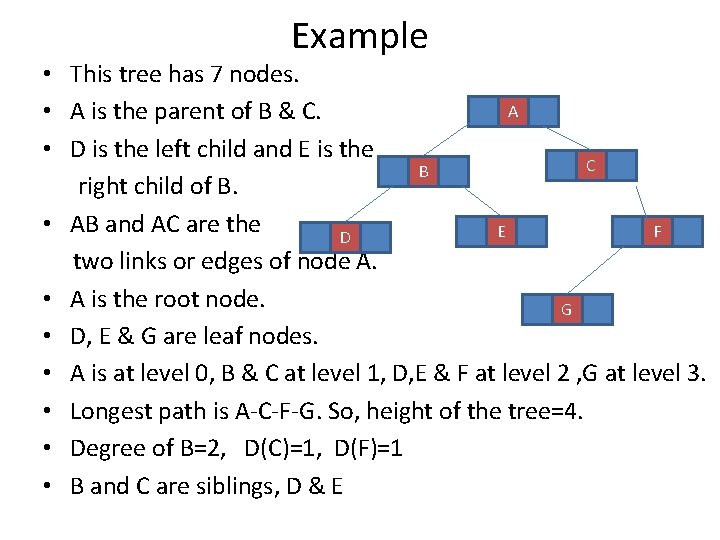
Example • This tree has 7 nodes. A • A is the parent of B & C. • D is the left child and E is the C B right child of B. • AB and AC are the E F D two links or edges of node A. • A is the root node. G • D, E & G are leaf nodes. • A is at level 0, B & C at level 1, D, E & F at level 2 , G at level 3. • Longest path is A-C-F-G. So, height of the tree=4. • Degree of B=2, D(C)=1, D(F)=1 • B and C are siblings, D & E

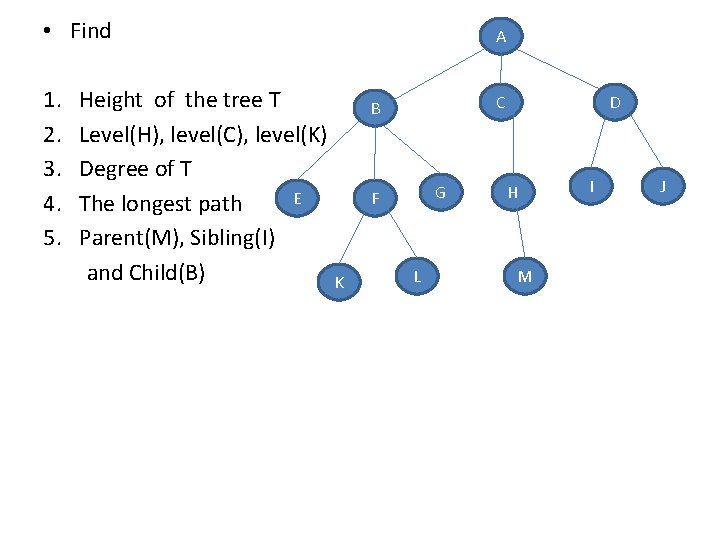
• Find 1. Height of the tree T 2. Level(H), level(C), level(K) 3. Degree of T E 4. The longest path 5. Parent(M), Sibling(I) and Child(B) K A C B G F L D H M I J

Definition • A tree T is defined as a finite set of one or more nodes such that: a) There is a specially designed node called the root, b) Remaining nodes are partitioned in to n (n>0) disjoint sets T 1, T 2, …, Tn , where each Ti is a tree. T 1, T 2, …, Tn are called sub trees of the root. A C B D T 1 E G F K L I H M T 2 T 3 J

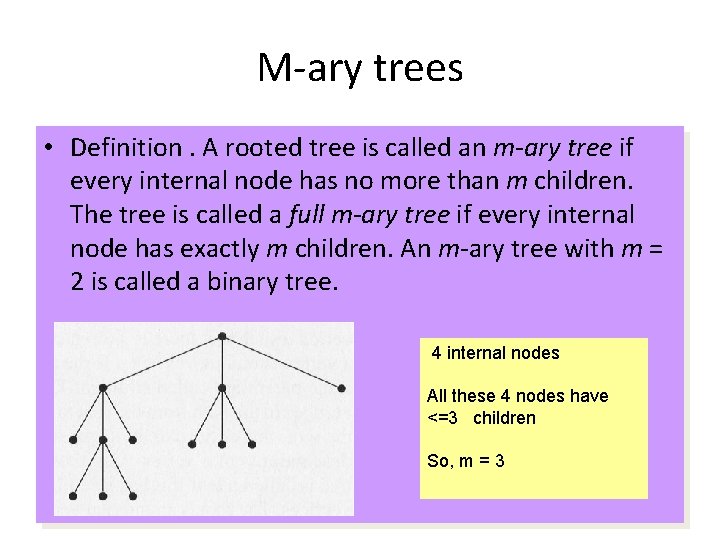
M-ary trees • Definition. A rooted tree is called an m-ary tree if every internal node has no more than m children. The tree is called a full m-ary tree if every internal node has exactly m children. An m-ary tree with m = 2 is called a binary tree. 4 internal nodes All these 4 nodes have <=3 children So, m = 3

Binary Trees • Special form of a tree. • A binary tree T is defined as a finite set of nodes such that: a) T is empty( called the empty binary tree) b) T contains a specially designed node called the root of T and the remaining nodes of T form two disjoint binary trees T 1 & T 2 which are called the left sub-tree & the right sub-tree respectively.

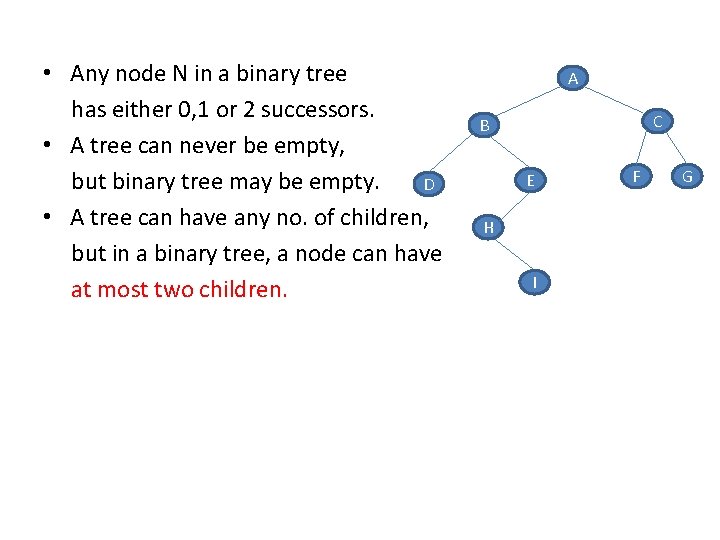
• Any node N in a binary tree has either 0, 1 or 2 successors. • A tree can never be empty, but binary tree may be empty. D • A tree can have any no. of children, but in a binary tree, a node can have at most two children. A C B E H I F G

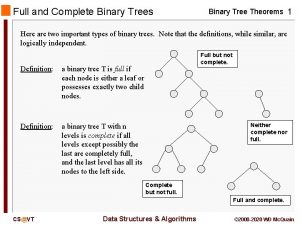
Two special situations of binary trees are: • Full binary tree & Complete binary tree. • Full binary tree – A binary tree is a full binary tree, if it contains maximum possible no. of nodes in all levels. Level Nodes 0 1 A 1 2 C B H F E D I J K L G M N O 2 4 3 8 – The maximum no. of nodes in each level l is: 2 l

• Complete binary tree – A binary tree is said to be complete binary tree, if all its level, except possibly the last level, have the maximum no. of possible nodes, and all the nodes in the last level appear as far left as possible. Level Nodes 0 1 1 2 A C B H F E D I J K L G 2 4 3 5

Properties of binary tree • In any binary tree, the maximum no. of nodes on level l is 2 l , where l>=0. • Maximum no. of nodes possible in a binary tree of height h is 2 h-1. • Minimum no. of nodes possible in a binary tree of height h is h. • For any non-empty binary tree, if n is the no. of nodes and e is the no. of edges, then, n= e+1

Representation of binary tree • Implicit & Explicit representation • Implicit representation – Sequential / Linear representation, using arrays. • Explicit representation – Linked list representation, using pointers.

Sequential representation • This representation is static. • Block of memory for an array is allocated, before storing the actual tree. • Once the memory is allocated, the size of the tree will be fixed. • Nodes are stored level by level, starting from the zeroth level. • Root node is stored in the starting memory location, as the first element of the array.

Sequential representation • Consider a linear array TREE Rules for storing elements in TREE are: 1. The root R of T is stored in location 1. 2. For any node with index i 1<i<=n: 1. PARENT(i)= i/2 For the node when i=1, there is no parent. 2. LCHILD(i)=2*i If 2* i >n, then i has no left child 3. RCHILD(i)=2*i+1 If 2*i+1>n, then i has no right child.

Sequential representation: Example 45 77 22 30 11 15 25 90 88 1 2 3 4 5 6 7 8 9 10 11 12 13 14 45 22 77 11 30 90 15 25 88

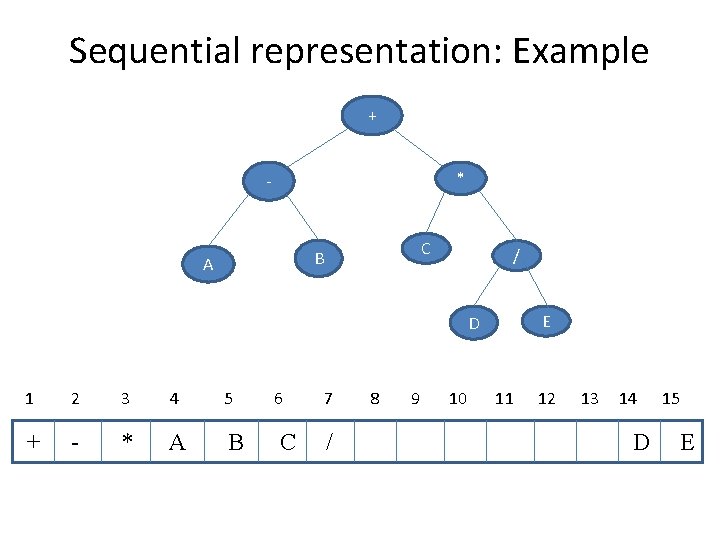
Sequential representation: Example + * - C B A / D E 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 + - * A B C / D E

Sequential representation- Advantages: 1. Any node can be accessed from any other node by calculating the index. 2. Here, data are stored simply without any pointers to their successor or predecessor. 3. Programming languages, where dynamic memory allocation is not possible(like BASIC, FROTRAN), array representation is only possible. 4. Inserting a new node and deletion of an existing node is easy.

Sequential representation- Disadvantages: 1. Other than full binary trees, majority of the array entries may be empty. 2. It allows only static representation. It is not possible to enhance the tree structure, if the array structure is limited.

Draw the tree structure whose array representation is given: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A B . C . D . . . E

Linked list representation • It consist of three parallel arrays DATA, LC and RC DATA LC RC • Each node N of T will correspond to a location K such that: – DATA[K] contains the data at the node N – LC[K] contains the location of the left child of node N – RC[K] contains the location of the right child of node N

Linked list representation • It consist of three parallel arrays DATA, LC and RC DATA LC RC • Each node N of T will correspond to a location K such that: – DATA[K] contains the data at the node N – LC[K] contains the location of the left child of node N – RC[K] contains the location of the right child of node N

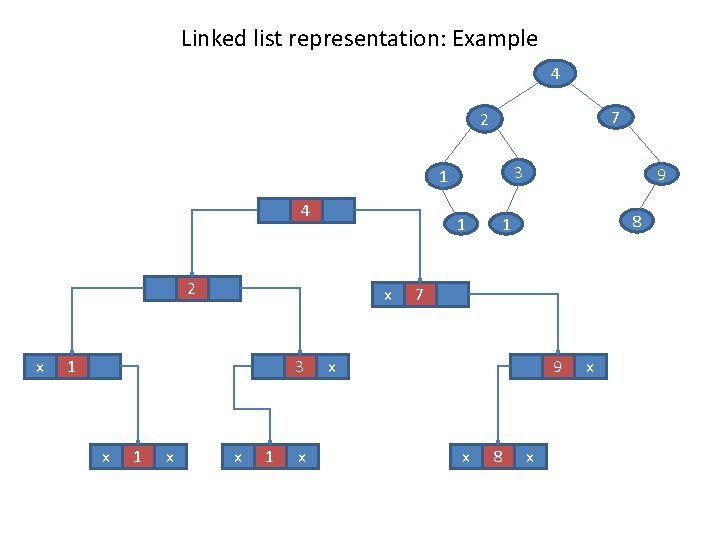
Linked list representation: Example 4 7 2 4 1 2 x 3 1 x 1 3 x 1 x 9 8 1 7 x 9 x 8 x x

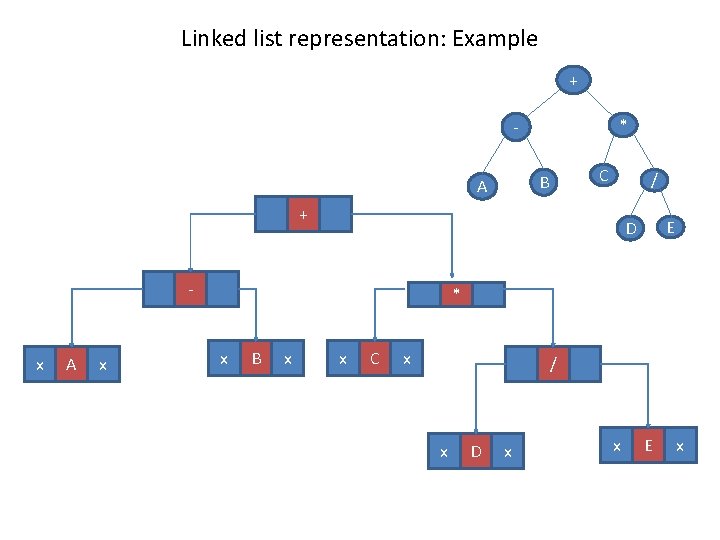
Linked list representation: Example + * - C B A / + - x A x E D * x B x x C x / x D x x E x

Exercise • Represent using array and linked list 5 (1). (2). 5 10 10 15 (3). 5 10 15 15

Skew binary tree • Consider a binary tree with n nodes. • If the maximum height possible hmax=n, then it is called skew binary tree. 5 5 (1). (2). 10 10 15 15

Binary tree traversals • Traversal is a process to visit all the nodes of a tree and may print their values too. • Because, all nodes are connected via edges (links) we always start from the root node. • That is, we cannot random access a node in tree. • There are three ways which we use to traverse a tree − 1. Preorder traversal (R, Tl, Tr) 2. Inorder traversal (Tl, R, Tr) 3. Postorder traversal (Tl, Tr , R)

Binary tree traversals • In pre-order, root is visited first(pre). • In in-order, root is visited in between left and right sub tree (in) • In post-order, root is visited last(post). • If the binary tree contains an arithmetic expression, then its inorder, pre-order and post-order traversals produce the infix, prefix and postfix expressions respectively.

Preorder traversal 1. Visit the root node R. 2. Traverse the left sub-tree of the root node R in preorder. 3. Traverse the right sub-tree of the root node R in preorder.

• • Preorder traversal In this traversal method, the root node is visited first, then left sub-tree and finally right sub-tree. • We start from A, and following pre-order traversal. • we first visit A itself and then move to its left sub-tree B. • B is also traversed pre-ordered And the process goes on until all the nodes are visited • The output of pre-order traversal of this tree will be − A→B→D→E→C→F→G

Algorithm preorder • Steps: 1. ptr=ROOT 2. If (ptrǂNULL) then 3. Visit(ptr) 4. preorder(ptr->LC) 5. preorder(ptr->RC) 6. endif

Inorder traversal 1. Traverse the left sub-tree of the root node R in inorder. 2. Visit the root node R. 3. Traverse the right sub-tree of the root node R in inorder.

Inorder traversal • In this traversal method, the left sub-tree is visited first. then root and then the right sub-tree. • We start from A, and following in-order traversal, we move to its left sub-tree B. • B is also traversed in-ordered. And the process goes on until all the nodes are visited. • The output of in-order traversal of this tree will be − D→B→E→A→F→C→G

Algorithm inorder • Steps: 1. ptr=ROOT 2. If (ptrǂNULL) then 3. inorder(ptr->LC) 4. Visit(ptr) 5. inorder(ptr->RC) 6. endif

Postorder traversal 1. Traverse the left sub-tree of the root node R in postorder. 2. Traverse the right sub-tree of the root node R in postorder. 3. Visit the root node R.

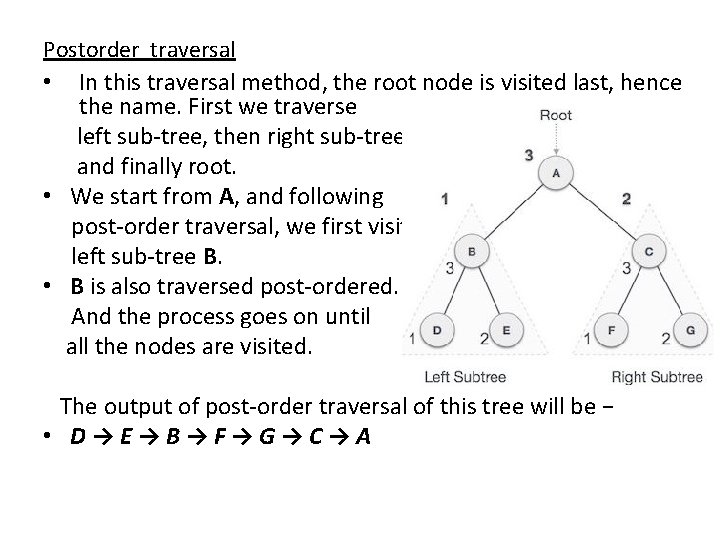
Postorder traversal • In this traversal method, the root node is visited last, hence the name. First we traverse left sub-tree, then right sub-tree and finally root. • We start from A, and following post-order traversal, we first visit left sub-tree B. • B is also traversed post-ordered. And the process goes on until all the nodes are visited. The output of post-order traversal of this tree will be − • D→E→B→F→G→C→A

Algorithm postorder • Steps: 1. ptr=ROOT 2. If (ptrǂNULL) then 3. postorder(ptr->LC) 4. postorder(ptr->RC) 5. Visit(ptr) 6. endif

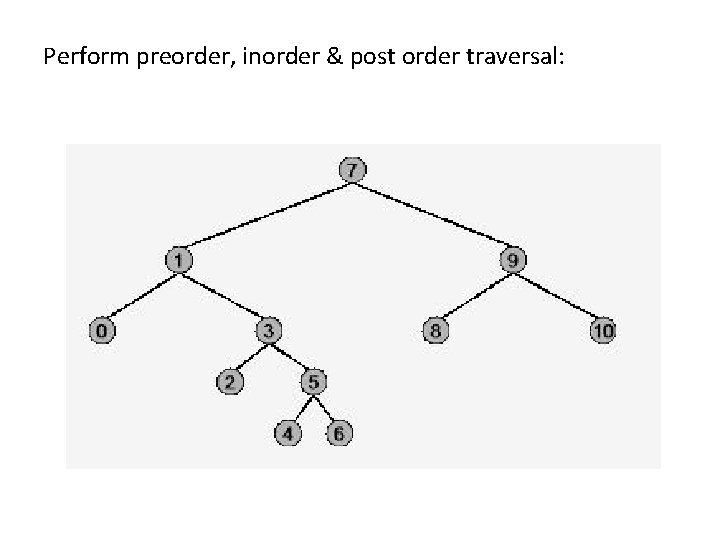
Perform preorder, inorder & post order traversal:

Non-recursive implementation of traversal algorithms using stack

Preorder traversal- non recursive algorithm using stack Preorder (Root) { if (Root == NULL) {Return} PUSH(Root) While ( stack not empty) do ptr = POP() If (ptr != NULL) then Visit (ptr-> Data) PUSH (ptr-> right child) PUSH (ptr-> left child) End if End While } Stop

In order- non recursive algorithm using stack Inorder (Root) { Ptr = Root While ( (Stack not empty) OR (ptr != NULL)) do If (ptr != NULL ) then PUSH (ptr) Ptr = ptr ->left child Else Ptr = POP() Visit (ptr -> Data) Ptr = ptr -> right child End If End While } Stop

Post order- non recursive algorithm using 2 stacks Post order (Root) { PUSH Stack 1 (Root) While (Stack 1 not empty) do Ptr = POP Stack 1() PUSH Stack 2(ptr) If (ptr-> left child != NULL) PUSH Stack 1(ptr->left child) If (ptr-> right child != NULL) PUSH Stack 1(ptr->right child) End While (Stack 2 not empty) do Ptr = POP Stack 2() Visit (ptr) End While } Stop

Formation of binary tree from its traversals • If the preorder traversal is given, the first node is the root node • If the post order traversal is given, then the last node is the root node. • Once the root node is identified, all the nodes in the left sub tree and the right sub tree of the root node can be identified.