Information Representation Floating Point Number Representation Lecture 7

Information Representation: Floating Point Number Representation Lecture # 7 Lecture 6: Floating Point Number Representation

Fractional Numbers Examples: 456. 7810 = 4 x 102 + 5 x 101 + 6 x 100 + 7 x 10 -1+8 x 10 -2 1011. 112= 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 + 1 x 2 -1 + 1 x 2 -2 = 8 + 0 + 2 + 1/2 + ¼ = 11 + 0. 5 + 0. 25 = 11. 7510 Conversion from binary number system to decimal system Examples: 111. 112 = 1 x 22 + 1 x 21 + 1 x 20 + 1 x 2 -1 + 1 x 2 -2 = 4 + 2 + 1/2 + ¼ = 7. 75 10 Examples: 11. 0112 2 1 0 -1 22 4 21 2 20 1 2 -1 ½ x x Lecture 6: Floating Point Number Representation -2 2 -2 ¼ x -3 2 -3 1/8 x

Conversion from decimal number system to binary system Examples: 7. 7510 = (? )2 Conversion of the integer part: same as before – repeated division by 2 7 / 2 = 3 (Q), 1 (R) 3 / 2 = 1 (Q), 1 (R) 1 / 2 = 0 (Q), 1 (R) 710 = 1112 2. Conversion of the fractional part: perform a repeated multiplication by 2 and extract the integer part of the result 0. 75 x 2 =1. 50 extract 1 0. 5 x 2 = 1. 0 extract 1 0. 7510 = 0. 112 write in the same order 0. 0 stop 1. Combine the results from integer and fractional part, 7. 7510 = 111. 112 How about choose some of 4 2 1 1/2 1/4 =0. 5 =0. 25 1/8 =0. 125 Examples: try 5. 625 B Lecture 6: Floating Point Number Representation

Fractional Numbers (cont. ) Exercise 1: Convert (0. 625)10 to its binary form Solution: 0. 625 x 2 = 1. 25 extract 1 0. 25 x 2 = 0. 5 extract 0 0. 5 x 2 = 1. 0 extract 1 0. 0 stop (0. 625)10 = (0. 101)2 Exercise 2: Convert (0. 6)10 to its binary form 0. 6 x 2 = 1. 2 extract 1 Solution: 0. 2 x 2 = 0. 4 extract 0 0. 4 x 2 = 0. 8 extract 0 0. 8 x 2 = 1. 6 extract 1 0. 6 x 2 = (0. 6)10 = (0. 1001 …)2 Lecture 6: Floating Point Number Representation

Fractional Numbers (cont. ) Exercise 3: Convert (0. 8125)10 to its binary form Solution: 0. 8125 x 2 = 1. 625 extract 1 0. 625 x 2 = 1. 25 extract 1 0. 25 x 2 = 0. 5 extract 0 0. 5 x 2 = 1. 0 extract 1 0. 0 stop (0. 8125)10 = (0. 1101)2 Lecture 6: Floating Point Number Representation

Fractional Numbers (cont. ) Errors One source of error in the computations is due to back and forth conversions between decimal and binary formats Example: (0. 6)10 + (0. 6)10 = 1. 210 Since (0. 6)10 = (0. 1001 …)2 Lets assume a 8 -bit representation: (0. 6)10 = (0. 1001)2 , therefore 0. 6 0. 1001 + 0. 6 + 0. 1001 1. 00110010 Lets reconvert to decimal system: (1. 00110010)b = 1 x 20 + 0 x 2 -1 + 0 x 2 -2 + 1 x 2 -3 + 1 x 2 -4 + 0 x 2 -5 + 0 x 2 -6 + 1 x 2 -7 + 0 x 2 -8 = 1 + 1/8 + 1/16 + 1/128 = 1. 1953125 Error = 1. 2 – 1. 1953125 = 0. 0046875 Lecture 6: Floating Point Number Representation

Floating Point Number Representation If x is a real number then its normal form representation is: x = f • Base E where f : mantissa E: exponent Example: 125. 3210 = 0. 12532 • 103 mantissa - 125. 3210 = - 0. 12532 • 103 0. 054610 = 0. 546 • 10 – 1 The mantissa is normalized, so the digit after the fractional point is non-zero. If needed the mantissa should be shifted appropriately to make the first digit (after the fractional point) to be non-zero & the exponent is properly adjusted. Lecture 6: Floating Point Number Representation

Example: 3 134. 1510 = 0. 13415 x 10 -2 0. 002110 = 0. 21 x 10 101. 11 B = 0. 011 B = AB. CDH= 0. 00 ACH= Lecture 6: Floating Point Number Representation

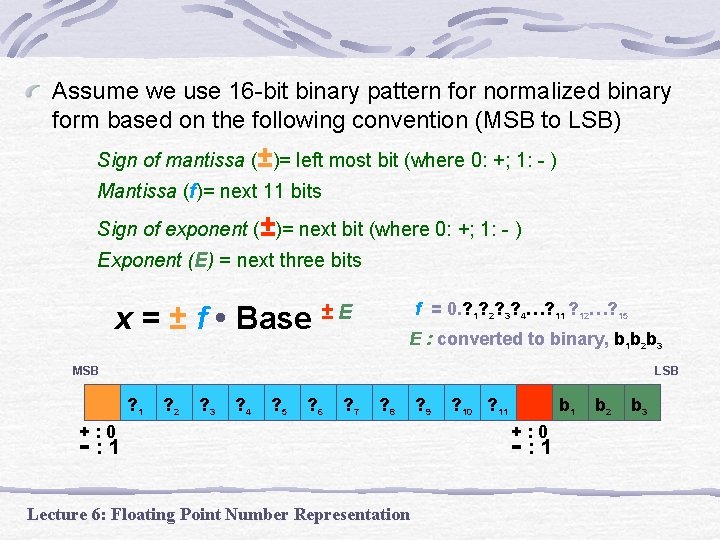
Assume we use 16 -bit binary pattern for normalized binary form based on the following convention (MSB to LSB) Sign of mantissa (±)= left most bit (where 0: +; 1: - ) Mantissa (f)= next 11 bits Sign of exponent (±)= next bit (where 0: +; 1: - ) Exponent (E) = next three bits x = ± f • Base f = 0. ? 1? 2? 3? 4…? 11 ? 12…? 15 ±E E : converted to binary, b 1 b 2 b 3 MSB LSB ? 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8 +: 0 - : 1 Lecture 6: Floating Point Number Representation ? 9 ? 10 ? 11 b 1 +: 0 - : 1 b 2 b 3

Floating Point Number Representation Question: How the computer expresses the 16 -bit approximation of 111010111111 in normalized binary form using the following convention Sign of mantissa = left most bit (where 0: +; 1: - ) Mantissa = next 11 bits Sign of exponent = next bit (where 0: +; 1: - ) Exponent = next three bits Answer: Step 1: Normalization 111010111111 = + 1. 11010111111 * 2 +3 Step 2: “Plant” 16 bits sign 1 bit mantissa 11 bits sign exponent 1 bit 3 bits the 16 bit floating point representation is 0 1110101 0 Lecture 6: Floating Point Number Representation 011