Multiplecriteria ranking using an additive value function constructed

Multiple-criteria ranking using an additive value function constructed via ordinal regresion : UTA method Roman Słowiński Poznań University of Technology, Poland Roman Słowiński

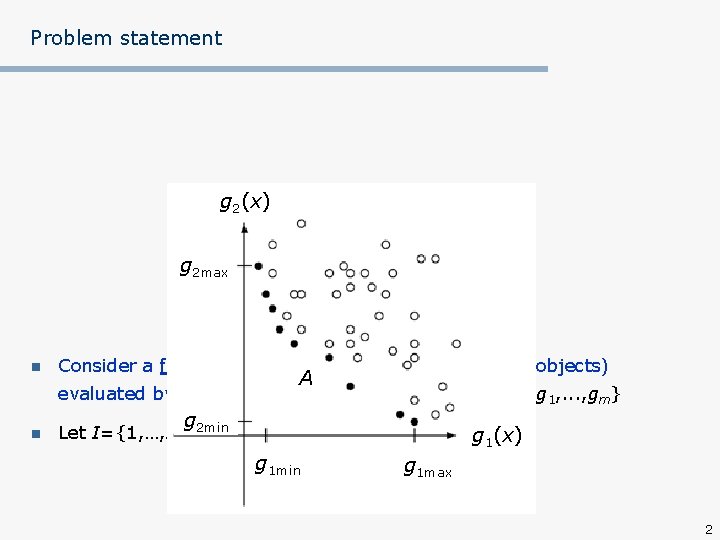
Problem statement g 2(x) g 2 max n Consider a finite set A of actions (actions, solutions, objects) A evaluated by m criteria from a consistent family F={g 1, . . . , gm} n g Let I={1, …, m} 2 min g 1(x) g 1 min g 1 max 2

What is a consistent family of criteria ? n A family of criteria F={g 1, . . . , gn} is consistent if it is: n Complete – if two actions have the same evaluations on all criteria, then they have to be indifferent, i. e. if for any a, b A, there is gi(a)~gi(b), i I, then a~b n Monotonic – if action a is preferred to action b (a b), and there is action c, such that gi(c) gi(a), i I, then c b n Non-redundant – elimination of any criterion from the family F should violate at least one of the above properties 3

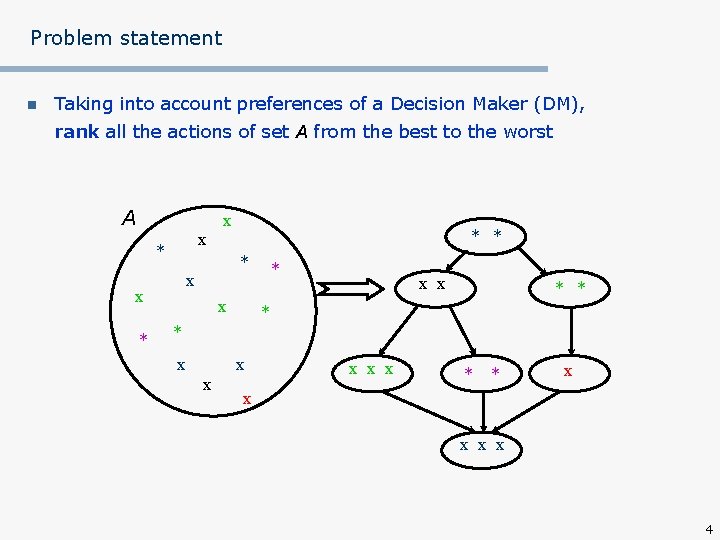
Problem statement n Taking into account preferences of a Decision Maker (DM), rank all the actions of set A from the best to the worst A x * * x x * * x x x 4

Dominance relation n Action a A is non-dominated (Pareto-optimal) if and only if there is no other action b A such that gi(b) gi(a), i I, and on at least one criterion j I, gi(b) gi(a) g 2(x) g 2 max nadir A g 2 min ideal g 1(x) g 1 min g 1 max 5

Criteria aggregation model = preference model n Dominance relation is too poor – it leaves many actions non-comparable n One can „enrich” the dominance relation, using preference information elicited from the Decision Maker n Preference information permits to built a preference model that aggregates the vector evaluations of elements of A 6

Why traditional MCDM methods may confuse their users ? n n Traditional MCDM methods require a rich and difficult preference information: n many intracriteria and intercriteria parameters: thresholds, weights, … n complete set of pairwise comparisons of actions on each criterion n complete set of pairwise comparisons of criteria n … They suppose the DM understands the logic of a particular aggregation model: n meaning of weights: substitution ratios or relative strengths n meaning of lotteries (ASSESS) n meaning of indifference, preference and veto thresholds (ELECTRE) n meaning of the ratio scale of the intensity of preference (AHP) n meaning of „neutral” and „good” levels on particular criteria (MACBETH) n … 7

Towards „easy” preference information n Traditional methods appear to be too demanding of cognitive effort of their users n This is why we advocate for methods requiring „easy” preference information n „Easy” means natural and even partial n Psychologists confirm that DMs are more confident exercising their decisions than explaining them 8

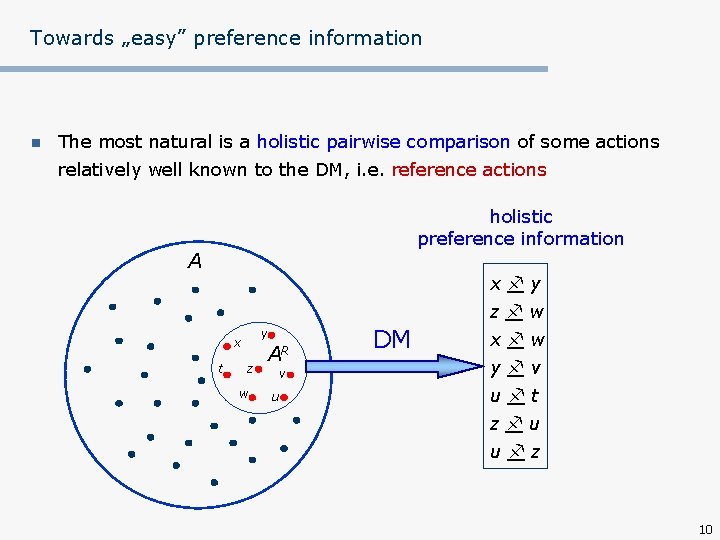
Towards „easy” preference information n The most natural is a holistic pairwise comparison of some actions relatively well known to the DM, i. e. reference actions A 9

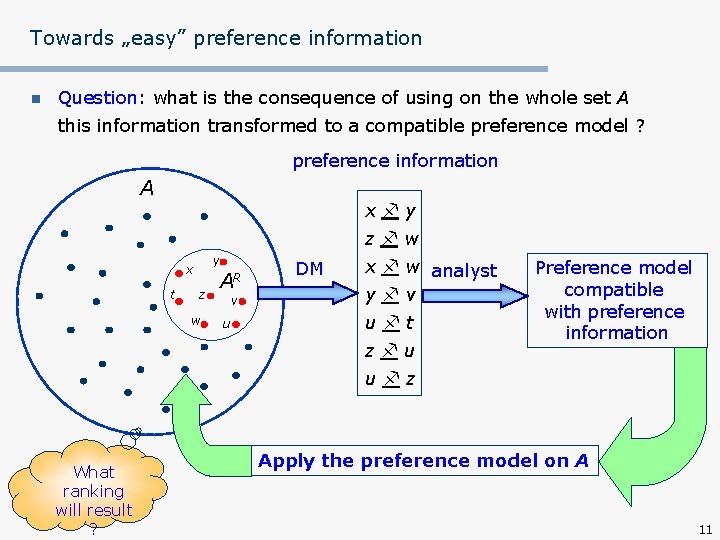
Towards „easy” preference information n The most natural is a holistic pairwise comparison of some actions relatively well known to the DM, i. e. reference actions holistic preference information A x y z w y x t z w AR v u DM x w y v u t z u u z 10

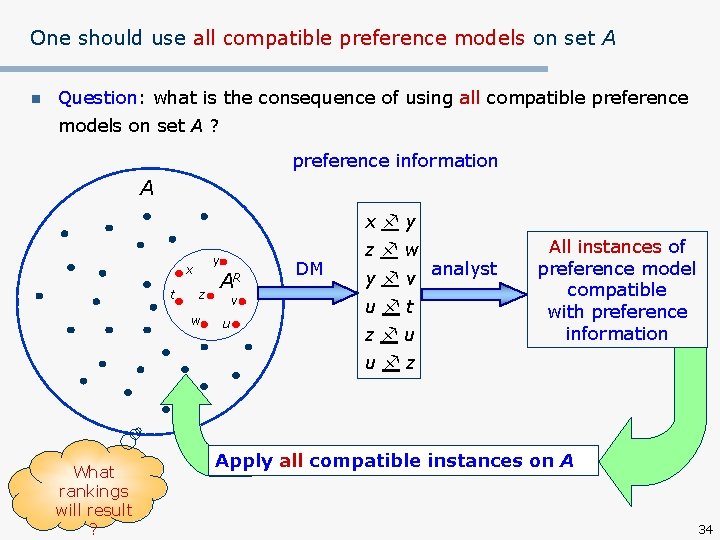
Towards „easy” preference information n Question: what is the consequence of using on the whole set A this information transformed to a compatible preference model ? preference information A x y z w y x t z w AR v u DM x w analyst y v u t z u Preference model compatible with preference information u z What ranking will result ? Apply the preference model on A 11

Aggregation paradigms n Disaggregation-aggregation (or regression) paradigm: The holistic preference on a subset AR A is known first, and then a compatible criteria aggregation model (compatible preference model) is inferred from this information to be applied on set A n Traditional aggregation paradigm: The criteria aggregation model (preference model) is first constructed and then applied on set A to get information about holistic preference 12

Aggregation paradigms n The disaggregation-aggregation paradigam has been introduced to MCDS by Jacquet-Lagreze & Siskos (1982) in the UTA method: the inferred criteria aggregation model is the additive value function with piecewise-linear marginal value functions n The disaggregation-aggregation paradigam is consistent with the „posterior rationality” principle by March (1988) and „learning from examples” used in AI and knowledge discovery n Other aggregation models inferred in this way: n Fishburn (1967) – trade-off weights n Mousseau & Słowiński (1998) – outranking relation (ELECTRE TRI) n Greco, Matarazzo & Słowiński (1999) – decision rules or trees (DRSA – Dominance-based Rough Set Approach) 13

Basic concepts and notation n n Gi – domain of criterion gi (Gi is finite or countably infinte) – evaluation space n x, y G – profiles of actions in evaluation space n – weak preference (outranking) relation on G: for each x, y G x y „x is at least as good as y” x y [x y and not y x] „x is preferred to y” x~y [x y and y x] „x is indifferent to y” 14

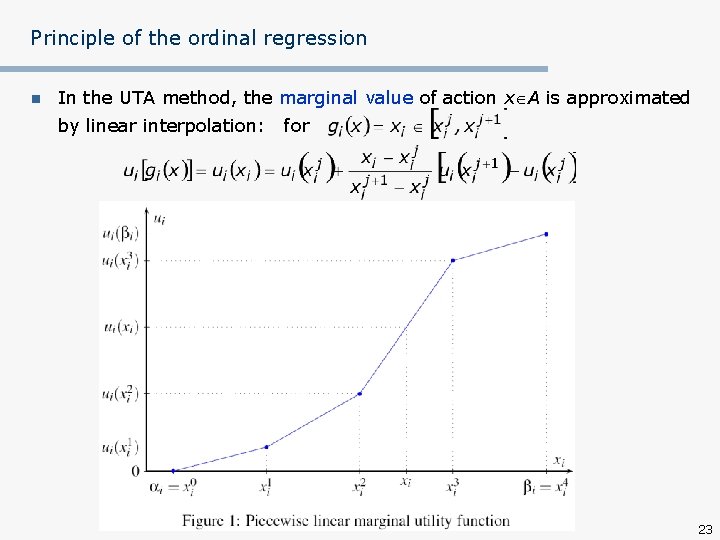
Reminder of the UTA method (Jacquet-Lagreze & Siskos, 1982) n For simplicity: Gi , i I, where I={1, …, m} n For each gi, Gi=[ i, i] is the criterion evaluation scale, i i , where i and i, are the worst and the best (finite) evaluations, resp. n Thus, A is a finite subset of G and n Additive value (or utility) function on G: for each x G where ui are non-decreasing marginal value functions, ui : Gi , i I 15

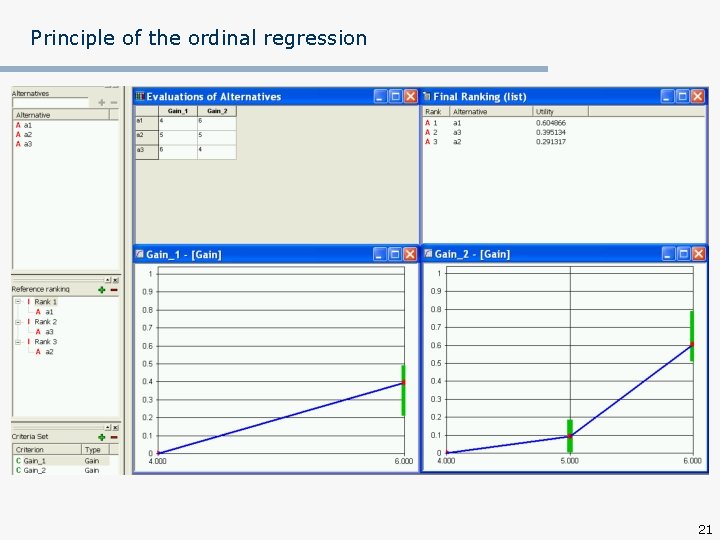
Principle of the ordinal regression - UTA n (Jacquet-Lagreze & Siskos, 1982) The preference information is given in form of a complete preorder on a subset of reference actions AR A, AR={x 1, x 2, . . . , xn} – the reference actions are rearranged such that xk xk+1 , k=1, . . . , n-1 x 1 A x 2 AR x 3 x 4 x 5 x 6 x 7 16

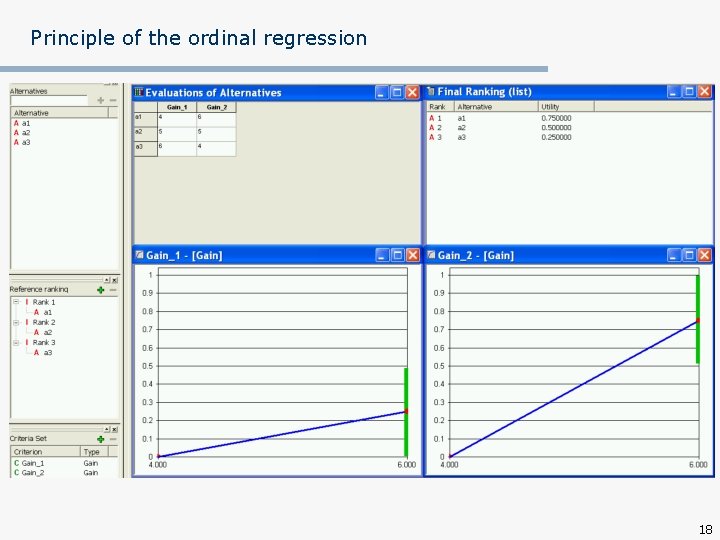
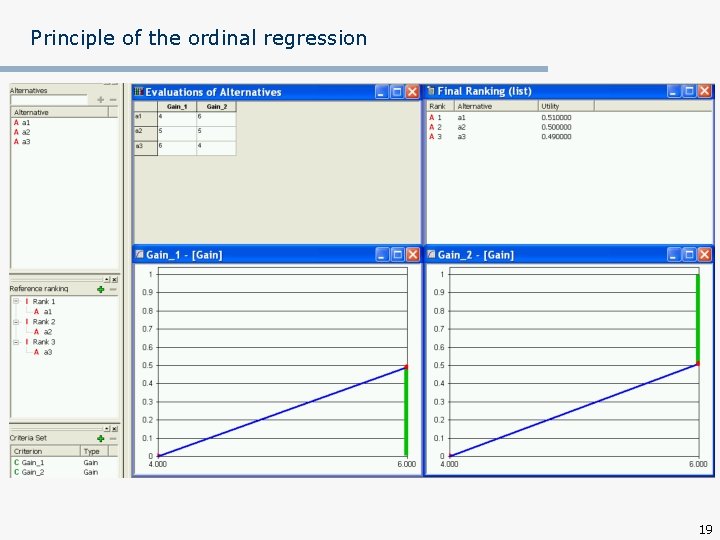
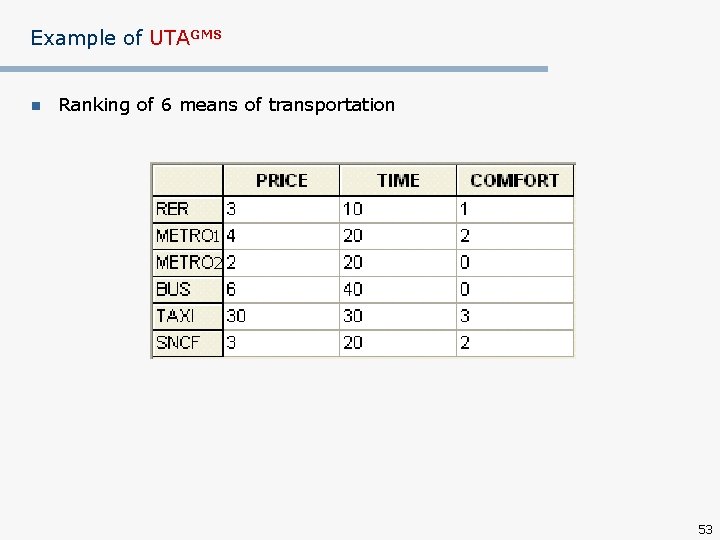
Principle of the ordinal regression n Example: Let AR={a 1, a 2, a 3}, G={Gain_1, Gain_2} Evaluation of reference actions on criteria Gain_1, Gain_2: Gain_1 Gain_2 a 1 4 6 a 2 5 5 a 3 6 4 Reference ranking: a 1 a 2 a 3 17

Principle of the ordinal regression 18

Principle of the ordinal regression 19

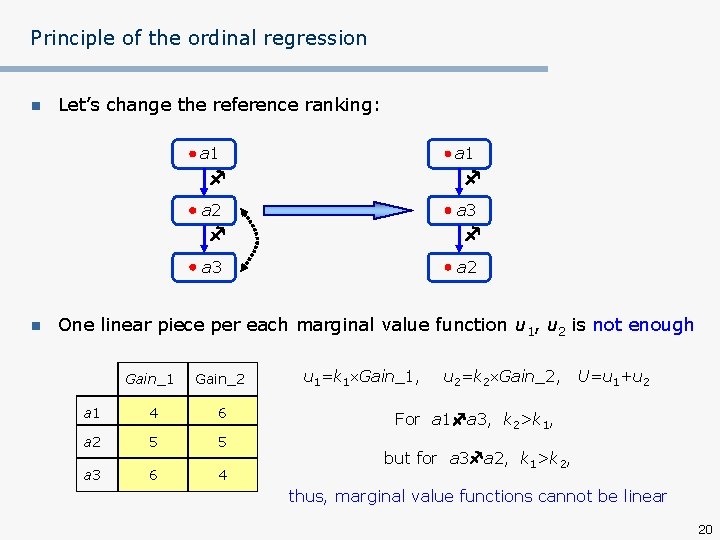
Principle of the ordinal regression n Let’s change the reference ranking: a 1 n a 2 a 3 a 2 One linear piece per each marginal value function u 1, u 2 is not enough Gain_1 Gain_2 a 1 4 6 a 2 5 5 a 3 6 4 u 1=k 1 Gain_1, u 2=k 2 Gain_2, U=u 1+u 2 For a 1 a 3, k 2>k 1, but for a 3 a 2, k 1>k 2, thus, marginal value functions cannot be linear 20

Principle of the ordinal regression 21

Principle of the UTA method n (Jacquet-Lagreze & Siskos, 1982) The comprehensive preference information is given in form of a complete preorder on a subset of reference actions AR A, AR={x 1, x 2, . . . , xn} – the reference actions are rearranged such that xk xk+1 , k=1, . . . , n-1 n The inferred value of each reference action x AR where + and - are potential errors of over- and under-estimation of the right value, resp. n The intervals [ i, i] are divided into i equal sub-intervals with the end points (i I) 22

Principle of the ordinal regression n In the UTA method, the marginal value of action x A is approximated by linear interpolation: for 23

UTA additive preference model 24

Principle of the UTA method n Ordinal regression principle for xk xk+1 , k=1, . . . , n-1 n Monotonicity of preferences n Normalization 25

Principle of the UTA method n The marginal value functions (breakpoint variables) are estimated by solving the LP problem k=1, . . . , n-1 (C) where is a small positive constant 26

Principle of the UTA method n If EUTA*=0, then the polyhedron of feasible solutions for ui(xi) is not empty and there exists at least one value function U[g(x)] compatible with the complete preorder on AR n If EUTA*>0, then there is no value function U[g(x)] compatible with the complete preorder on AR – three possible moves: n increasing the number of linear pieces i for ui(xi) n revision of the complete preorder on AR n post-optimal search for the best function with respect to Kendall’s in the area EUTA*+ Jacquet-Lagreze & Siskos (1982) polyhedron of constraints (C) EUTA*+ EUTA= EUTA* 27

Współczynnik Kendalla n Do wyznaczania odległości między preporządkami stosuje się miarę Kendalla n Przyjmijmy, że mamy dwie macierze kwadratowe R i R* o rozmiarze m m, gdzie m = |AR|, czyli m jest liczbą wariantów referencyjnych n macierz R jest związana z porządkiem referencyjnym podanym przez decydenta, n macierz R* jest związana z porządkiem dokonanym przez funkcję użyteczności wyznaczoną z zadania PL (zadania regresji porządkowej) n Każdy element macierzy R, czyli rij (i, j=1, . . , m), może przyjmować wartości: n To samo dotyczy elementów macierzy R* n Tak więc w każdej z tych macierzy kodujemy pozycję (w porządku) wariantu a względem wariantu b 28

Współczynnik Kendalla n Następnie oblicza się współczynnik Kendalla : gdzie dk(R, R*) jest odległością Kendalla między macierzami R i R*: n Stąd -1, 1 n Jeżeli = -1, to oznacza to, że porządki zakodowane w macierzach R i R* są zupełnie odwrotne, np. macierz R koduje porządek a b c d, a macierz R* porządek d c b a n Jeżeli = 1, to zachodzi całkowita zgodność porządków z obydwu macierzy. W tej sytuacji błąd estymacji funkcji użyteczności F*=0 n W praktyce funkcję użyteczności akceptuje się, gdy 0. 75 29

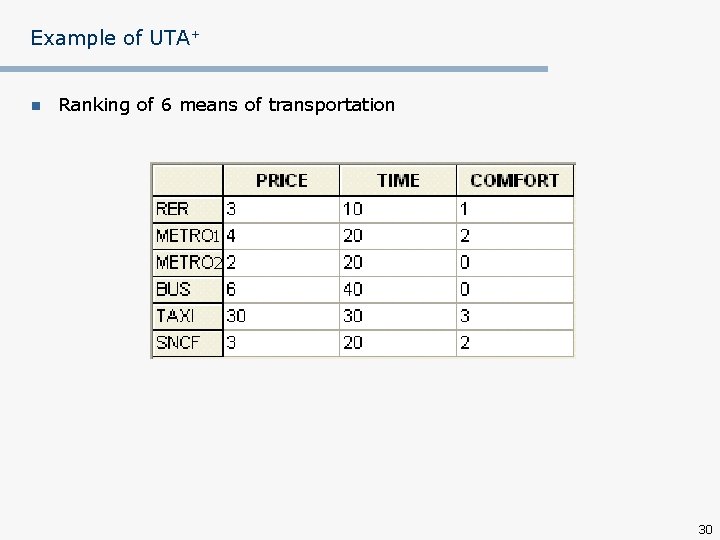
Example of UTA+ n Ranking of 6 means of transportation 1 2 30

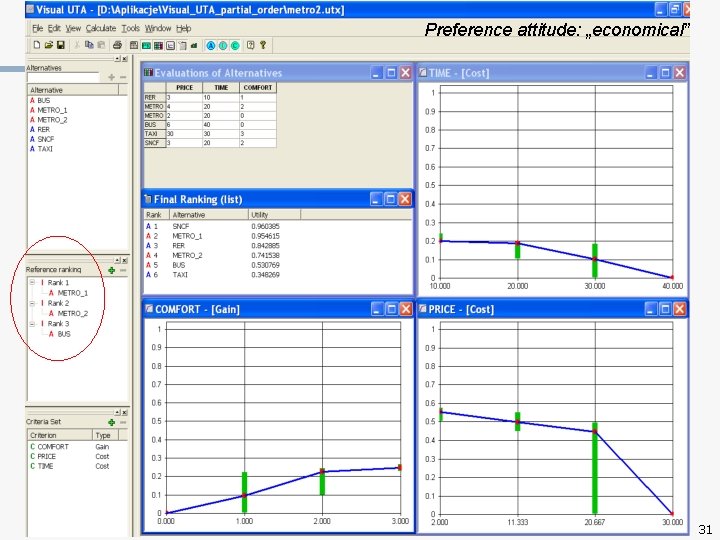
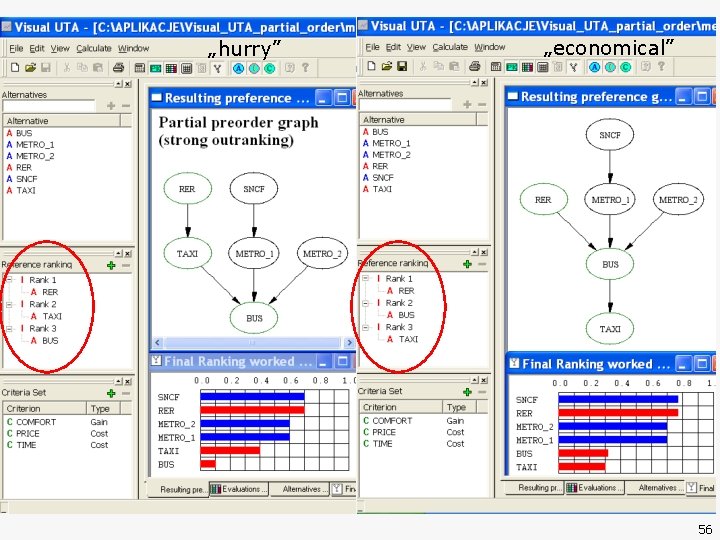
Preference attitude: „economical” 31

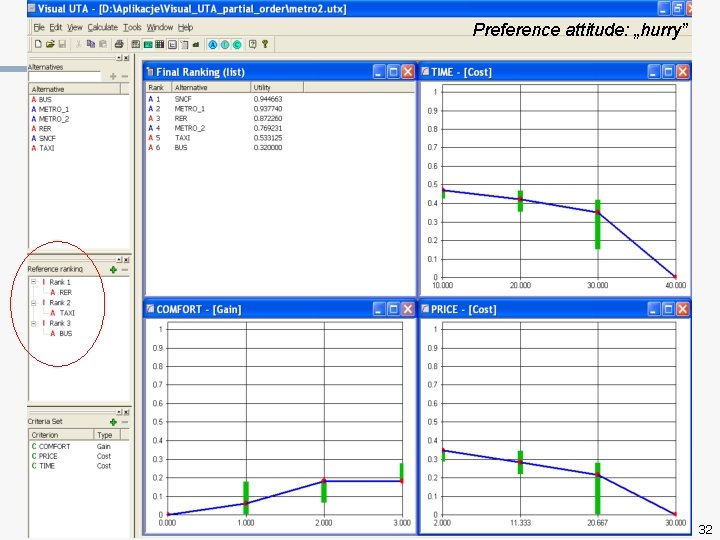
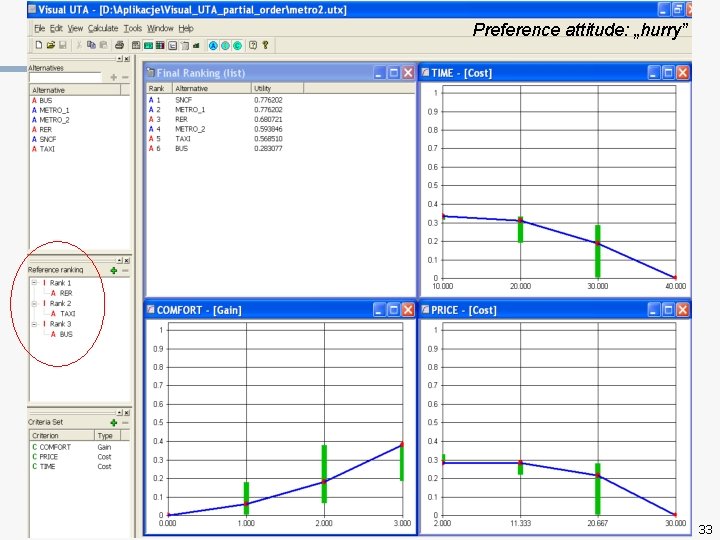
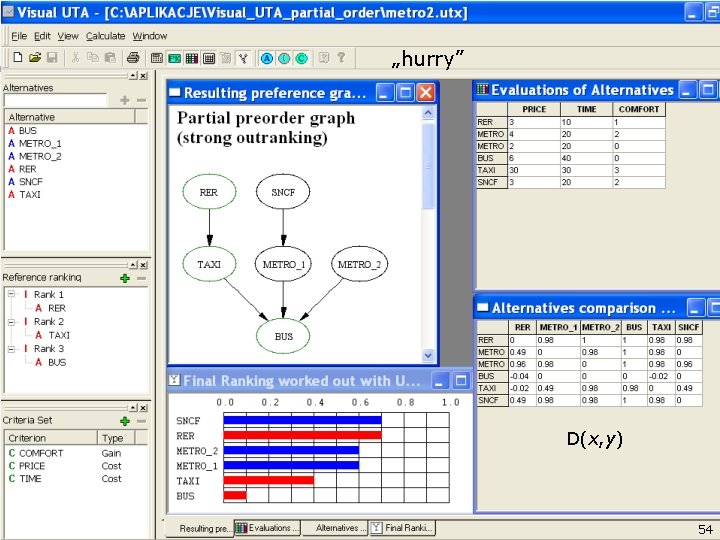
Preference attitude: „hurry” 32

Preference attitude: „hurry” 33

One should use all compatible preference models on set A n Question: what is the consequence of using all compatible preference models on set A ? preference information A x y y x t z w AR v u DM z w y v u t z u analyst All instances of preference model compatible with preference information u z What rankings will result ? Apply all compatible instances on A 34

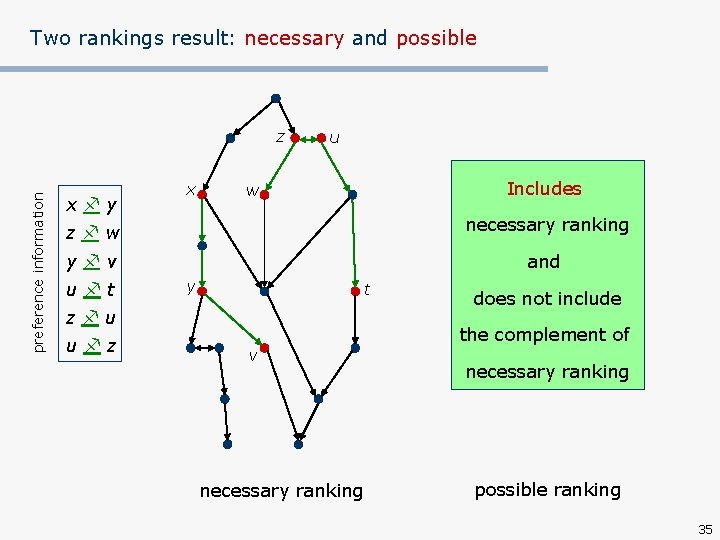
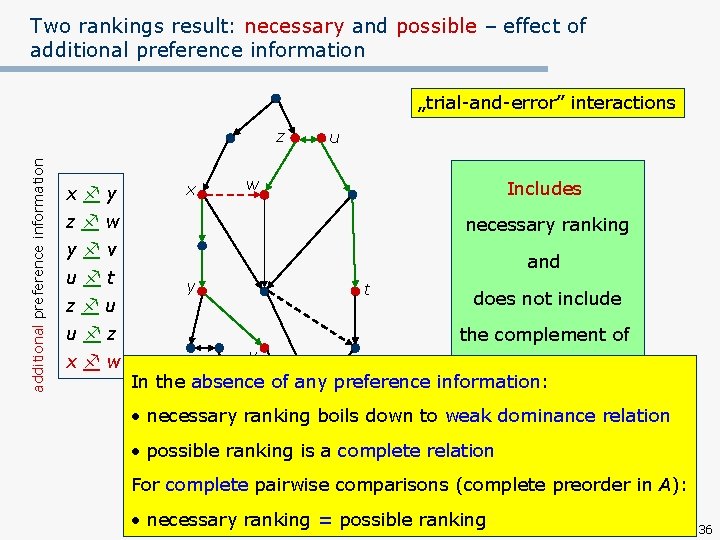
Two rankings result: necessary and possible preference information z x y x u Includes w z w necessary ranking y v and u t y t z u u z v necessary ranking does not include the complement of necessary ranking possible ranking 35

Two rankings result: necessary and possible – effect of additional preference information „trial-and-error” interactions additional preference information z x y x u w Includes z w necessary ranking y v u t z u and y t u z x w v does not include the complement of necessary ranking In the absence of any preference information: • necessary ranking boils down to weak dominance relation • possible ranking is a complete relation necessary ranking possible preorder ranking in A): For complete pairwise comparisons (complete enriched impoverished • necessary ranking = possible ranking 36

The UTAGMS method (Greco, Mousseau & Słowiński 2004) n The preference information is a partial preorder on a subset of reference actions AR A n A value function is called compatible if it is able to restore the partial preorder reference actions from AR n Each compatible value function induces a ranking on set A n In result, one obtains two rankings on set A, such that for any pair of actions (x, y) A: n x N y: x is ranked at least as good as y iff U(x) U(y) for all value functions compatible with the preference information (necessary weak preference relation N - a partial preorder on A) n x P y: x is ranked at least as good as y iff U(x) U(y) for at least one value function compatible with the preference information (possible weak preference relation P - a strongly complete and negatively transitive binary relation on A) 37

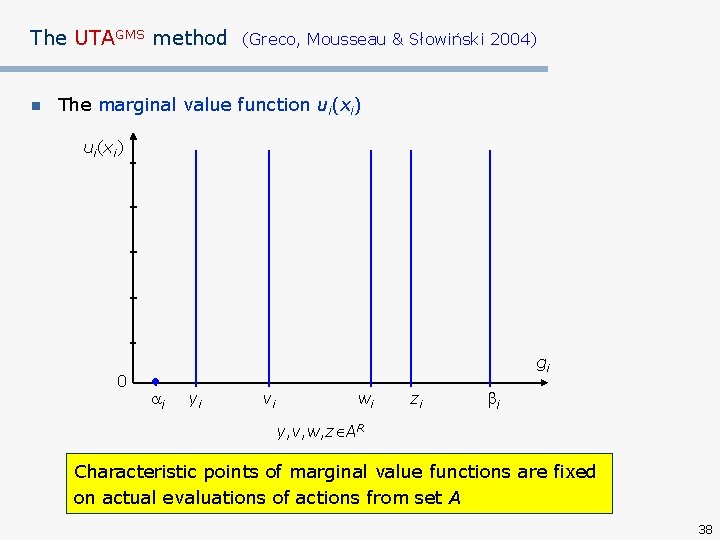
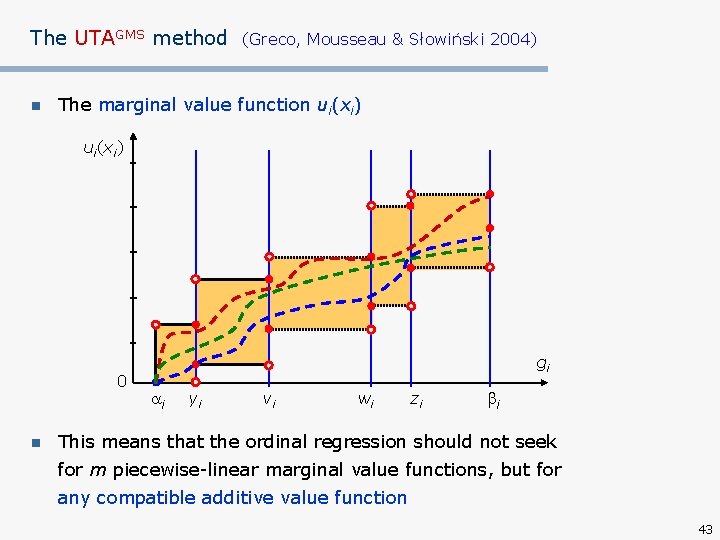
The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) 0 gi i yi vi wi zi i y, v, w, z AR Characteristic points of marginal value functions are fixed on actual evaluations of actions from set A 38

The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) ? ? ? ? ? 0 gi i yi vi wi zi i y, v, w, z AR Marginal values in characteristic points are unknown 39

The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) 0 gi i yi vi wi zi i y, v, w, z AR In fact, they are intervals, because all compatible value functions are considered 40

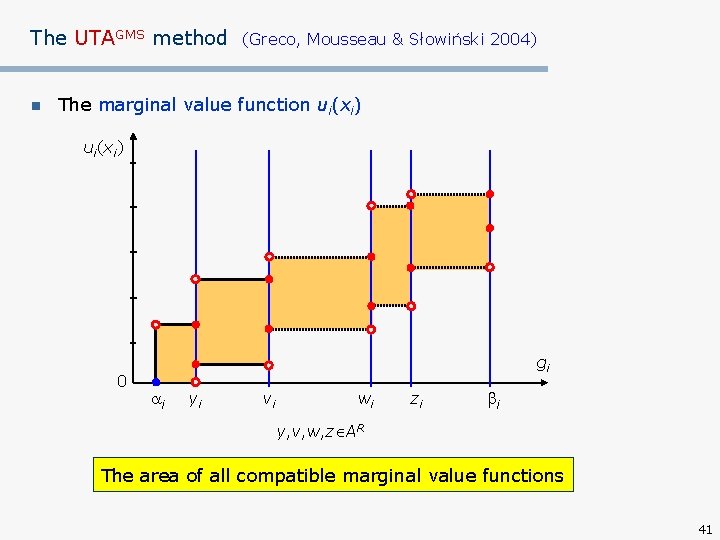
The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) 0 gi i yi vi wi zi i y, v, w, z AR The area of all compatible marginal value functions 41

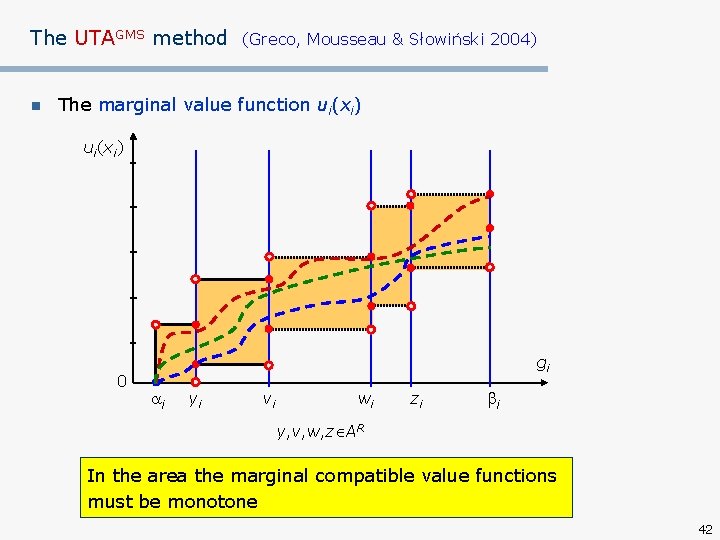
The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) 0 gi i yi vi wi zi i y, v, w, z AR In the area the marginal compatible value functions must be monotone 42

The UTAGMS method n (Greco, Mousseau & Słowiński 2004) The marginal value function ui(xi) 0 n gi i yi vi wi zi i This means that the ordinal regression should not seek for m piecewise-linear marginal value functions, but for any compatible additive value function 43

The UTAGMS method n Let i be a permutation on the set of actions AR {x, y} that reorders them according to increasing evaluation on criterion gi: where n n if AR {x, y}= , then =n+2 n if AR {x, y}={x} or AR {x, y}={y}, then =n+1 n if AR {x, y}={x, y}, then =n The characteristic points of ui(xi), i I, are then fixen in: 44

The UTAGMS method n For any pair of actions (x, y) A, and for available preference information concerning AR, preference of x over y is determined by compatible value functions U verifying set E(x, y) of constraints: a b a a b b a, b AR E(x, y) a a a where is a small positive constant n For all (x, y) A, E(x, y) = E(y, x) 45

The UTAGMS method n N means necessary (strong) preference relation n Given a pair of actions x, y A x Ny d(x, y) 0 where n d(x, y) 0 means that for all compatible value functions x is at least as good as y n For x, y AR : x y x Ny 46

The UTAGMS method n P means possible (weak) preference relation n Given a pair of actions x, y A x Py D(x, y) 0 where n D(x, y) 0 means that for at least one compatible value function x is at least as good as y n For x, y AR : x y not y Px 47

The UTAGMS method n Some properties: n x Ny x Py n N is a partial preorder (i. e. N is reflexive and transitive) n P is strongly complete (i. e. for all x, y A, x Py or y Px) and negatively transitive (i. e. for all x, y, z A, not x Py and not y Pz not x Pz ), (in general, P is not transitive) n d(x, y) = Min{U(x)–U(y)} = –Max{–[U(x)–U(y)]} = = –Max{U(y)–U(x)} = –D(y, x) 48

Proof of transitivity of N n d(x, y)>0 means: Min{U(x)-U(y)}>0 n This is equivalent to the fact: for all value functions compatible with the reference preorder, U(x)>U(y) n The set of all compatible value functions is the same for calculation of d(x, y) for any pair x, y A n Suppose, the transitivity of N is not true, i. e. for x, y, z A Min{U(x)-U(y)}>0, Min{U(y)-U(z)}>0, but Min{U(x)-U(z)}<0 n This means that U(x)-U(z) has achieved a minimum value d(x, z)<0 for a value function denoted by U*, such that U*(x)<U*(z), while U*(x)>U*(y) and U*(y)>U*(z) n In other words, U*(x)>U*(y)>U*(z)>U*(x) n This is a contradiction, so N is transitive 49

The UTAGMS method n Elaboration of the final ranking: n for the necessary preference relation being a partial preorder ( N is supported by all compatible value functions) preference: x Ny if x Ny and not y Nx indifference: x Ny if x Ny and y Nx incomparability: x ? y if not x Ny and not y Nx n for the possible preference relation being complete ( P is supported by at least one compatible value function) n preference: x Py if x Py and not y Px indifference: x Py if x Py and y Px N. B. It is impossible to infer one ranking from another because strong and weak outranking relations are not dual 50

The UTAGMS method – final ranking (partial preorder) N N N n N N N Final ranking corresponding to necessary (strong) preference : 51

The UTAGMS method – final ranking (complete preorder) n Final ranking corresponding to possible (weak) preference : P P P P P 52

Example of UTAGMS n Ranking of 6 means of transportation 1 2 53

„hurry” D(x, y) 54

„hurry” „economical” 56

Nested ranking with different credibility levels n Reference rankings in growing sets: with credibility levels ordered decreasingly n The reference ranking of alternatives from ARi does not change in ARi+1, i=1, …, p-1 n Each time we pass from ARi to ARi+1, we add to (E) new constraints concerning alternatives from {ARi+1 ARi} n If d(x, y)<0 in iteration i turns to d(x, y)>0 in iteration i+1, then we assign to x Ny the credibility level corresponding to ranking i+1 n In this way we get a set of nested partial preorders n In fact, we get a fuzzy partial preorder N~ with respect to credibility: for all x, y, z A, Min{Cr(x N~y), Cr(y N~z)} Cr(x N~z), thus N~ is min-transitive and reflexive 57

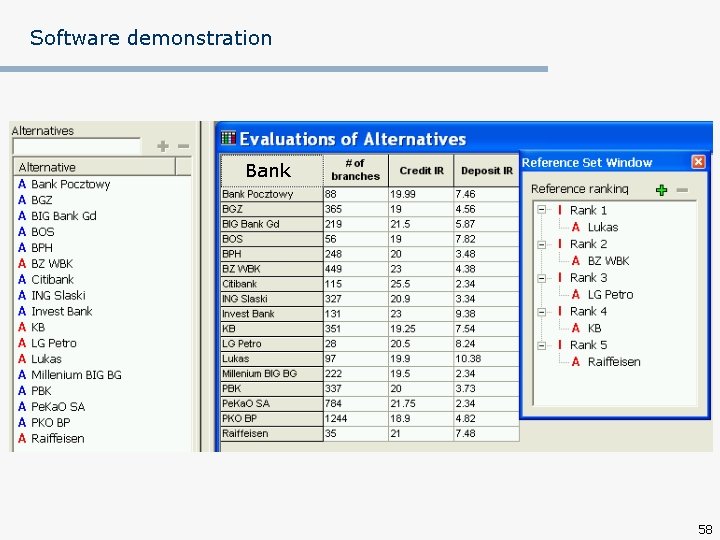
Software demonstration Bank 58

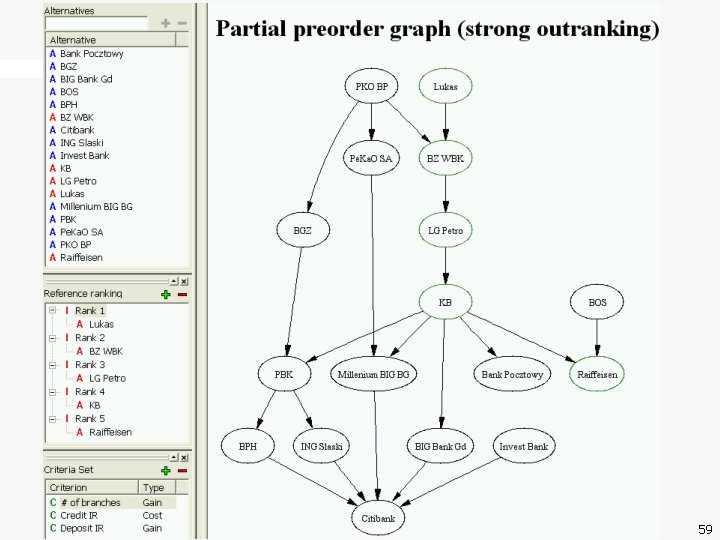
59

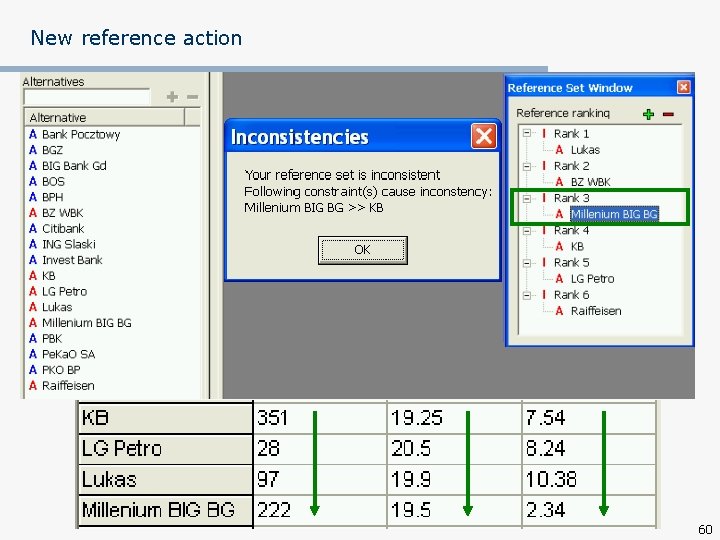
New reference action 60

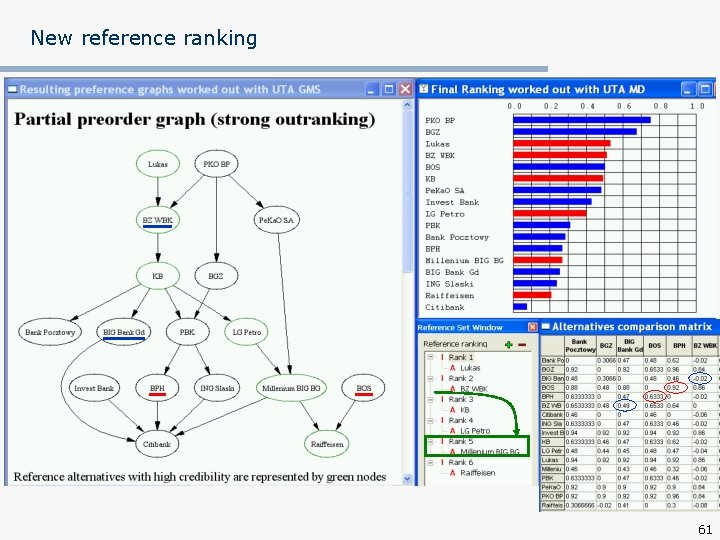
New reference ranking 61

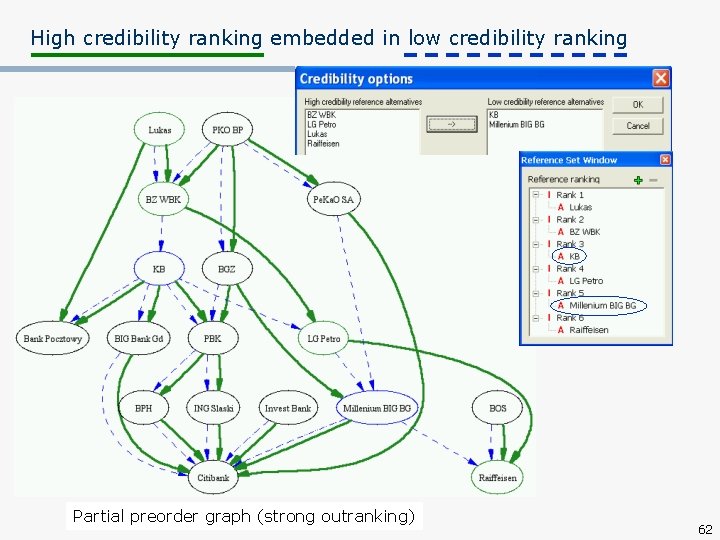
High credibility ranking embedded in low credibility ranking Partial preorder graph (strong outranking) 62

GRIP – Generalized Regression with Intensities of Preference (Figueira, Greco, Słowiński 2006) n GRIP extends the UTAGMS method by adopting all features of UTAGMS and by taking into account additional preference information : n comprehensive comparisons of intensities of preference between some pairs of reference actions, e. g. „x is preferred to y at least as much as w is preferred to z” n partial comparisons of intensities of preference between some pairs of reference actions on particular criteria, e. g. „x is preferred to y at least as much as w is preferred to z, on criterion gi F” 63

GRIP – Generalized Regression with Intensities of Preference n DM is supposed to provide the following preference information : n a partial preorder on AR, such that x, y AR x y „x is at least as good as y” = not -1, n = -1 a partial preorder * on AR AR, such that x, y, w, z AR (x, y) * (w, z) „x is preferred to y at least as much as w is preferred to z” * = * not *-1, n * = * *-1 a partial preorder i* on AR AR, i=1, . . . , m, such that x, y, w, z AR (x, y) i* (w, z) „x is preferred to y at least as much as w is preferred to z, on criterion gi F”, i* = i* not i*-1, i* = i* i*-1 64

GRIP – new contraints of the ordinal regression LP problem n A value function U : [0, 1] is called compatible if it satisfes the constraints corresponding to DM’s preference information: a) U(x) U(y) iff x y b) U(x) > U(y) iff x y c) U(x) = U(y) iff x y d) U(x) – U(y) U(w) – U(z) iff (x, y) * (w, z) e) U(x) – U(y) > U(w) – U(z) iff (x, y) * (w, z) f) U(x) – U(y) = U(w) – U(z) iff (x, y) * (w, z) g) ui(x) ui(y) iff x i y, i I h) ui(x) – ui(y) ui(w) – ui(z) iff (x, y) i* (w, z), i I i) ui(x) – ui(y) > ui(w) – ui(z) iff (x, y) i* (w, z), i I j) ui(x) – ui(y) = ui(w) – ui(z) iff (x, y) i* (w, z), i I 65

GRIP – new contraints of the ordinal regression LP problem n Moreover, the following normalization constraints should also be taken into account: k) ui( i)=0, i I l) 66

GRIP – new contraints of the ordinal regression LP problem n If constraints a) – l) are consistent, then we get two weak preference relations N and P , and two binary relations comparing intensity of preference *N and *P : n for all x, y A, a necessary weak preference relation, x N y: U(x) U(y) for all compatible value functions n for all x, y A, a possible weak preference relation, x P y: U(x) U(y) for at least one compatible value function n for all x, y, w, z A, a necessary relation of preference intensity, (x, y) *N (w, z): [U(x) – U(y)] – [U(w) – U(z)] 0 for all compatible value functions n for all x, y, w, z A, a possible relation of preference intensity, (x, y) *P (w, z): [U(x) – U(y)] – [U(w) – U(z)] 0 for at least one compatible value function 67

GRIP – fundamental properties of N, P, *N, *P Theorem: If constaraints a) – l) are satisfied, then the properties hold: 1. For all x, y A, x N y x P y 2. For all x, y AR, x y x N y 3. N is a partial preorder (i. e. the relation is transitive and reflexive) and P is strongly complete and negatively transitive 4. For all x, y, z A, [x N y and y P z] x P z 5. For all x, y, z A, [x P y and y N z] x P z 6. For all x, y, w, z A, (x, y) *N (w, z) (x, y) *P (w, z) 7. For all x, y, w, z A, (x, y) * (w, z) (x, y) *N (w, z) 8. *N is a partial preorder and *P is strongly complete and negatively transitive 9. For all x, y, w, z, r, s A, [(x, y) *N (w, z) and (w, z) *P (r, s)] (x', y) *P (r, s) 10. For all x, y, w, z, r, s A, [(x, y) *P (w, z) and (w, z) *N (r, s)] (x, y) *P (r, s) 11. For all x, x’, y, w, z A, [x’ N x and (x, y) *N (w, z)] (x’, y) *N (w, z) 12. For all x, x’, y, w, z A, [x’ N x and (x, y) *P (w, z)] (x’, y) *P (w, z) 13. For all x, x’, y, w, z A, [x’ P x and (x, y) *N (w, z)] (x’, y) *P (w, z) 68

GRIP – fundamental properties of N, P, *N, *P 14. For all x, y, y’, w, z A, [y N y’ and (x, y) *N (w, z)] (x, y’) *N (w, z) 15. For all x, y, y’, w, z A, [y N y’ and (x, y) *P (w, z)] (x, y’) *P (w, z) 16. For all x, y, y’, w, z A, [y P y’ and (x, y) *N (w, z)] (x, y’) *P (w, z) 17. For all x, y, w, w’, z A, [w N w’ and (x, y) *N (w, z)] (x, y) *N (w’, z) 18. For all x, y, w, w’, z A, [w N w’ and (x, y) *P (w, z)] (x, y) *P (w’, z) 19. For all x, y, w, w’, z A, [w P w’ and (x, y) *N (w, z)] (x, y) *P (w’, z) 20. For all x, y, w, z, z’ A, [z’ N z and (x, y) *N (w, z)] (x, y) *N (w, z’) 21. For all x, y, w, z, z’ A, [z’ N z and (x, y) *P (w, z)] (x, y) *P (w, z’) 22. For all x, y, w, z, z’ A, [z’ P z and (x, y) *N (w, z)] (x, y) *P (w, z’) 23. For all x, x’, y A, (x’, y) *N (x, y) x’ N x 24. For all x, x’, y A, (x’, y) *P (x, y) x’ P x 25. For all x, y, y’ A, (x, y) *N (x, y’) y’ N y 26. For all x, y, y’ A, (x, y) *P (x, y’) y’ P y 69

GRIP – the linear programming problem n In order to verify the truth or falsity of necessary and possible weak preference relations N, P and *N, *P, one can use LP n LP does not permit strict inequalities, such as b), e), i) They must be rewritten as: b’) U(x) U(y) + e’) U(x) – U(y) U(w) – U(z) + i’) ui(x) – ui(y) ui(w) – ui(z) + where >0 (small value) n In UTA and in UTAGMS the result is dependent on the value of n We want to make the result of GRIP independent of 70

GRIP – the linear programming problem n The following result will be useful (see e. g. Marichal & Roubens 2000): n Proposition: x is a solution of the linear system, # if there exists >0, such that In particular, a solution exists, iff the following LP Max has optimal solution (x*, *), where *>0. Then, x* is a solution of # 71

GRIP – the linear programming problem n According to the Proposition, if constraints b), e), i) are considered, in order to verify the truth or falsity of N and P , one should : Max subject to constraints a)–l), with b), e), i) written as b’), e’), i’) n If maximal *>0, the set of compatible value functions is not empty n Then, to verify the truth or falsity of x Py, for any x, y A, one should : Max subject to constraints a)–l), with b), e), i) written as b’), e’), i’) and U(x) U(y) n Maximal *>0 x Py n This means that there exists at least one compatible value function satisfying the hypothesis U(x) U(y) 72

GRIP – the linear programming problem n In order to verify the truth or falsity of x Ny, rather than to check directly that for each compatible value function U(x) U(y), we make sure that among the compatible value functions there is no one such that U(x) < U(y) : Max subject to constraints a)–l), with b), e), i) written as b’), e’), i’) and U(y) U(x) + n Maximal *≤ 0 x Ny 73

GRIP – the linear programming problem n Analogously, if constraints b), e), i) are considered, in order to verify the truth or falsity of (x, y) *P(w, z) for any x, y, w, z A, one should : Max subject to constraints a)–l), with b), e), i) written as b’), e’), i’) and U(x) U(y) U(w) U(z) n n Maximal *>0 (x, y) *P(w, z) In order to verify the truth or falsity of (x, y) *N(w, z) for any x, y, w, z A, one should : Max subject to constraints a)–l), with b), e), i) written as b’), e’), i’) and U(w) U(z) U(x) U(y) + n Maximal *≤ 0 (x, y) *N(w, z) n The value of * is not meaningful – the result does not depend on it! 74

Comparison of GRIP and MACBETH (Bana e Costa & Vansnick 1994) GRIP • Ordinal comprehensive preference inf. on pairwise comparison of some Preference information reference actions: x y, x, y AR • Absolute qualitative judgement of intensity of preference for some pairs of reference actions – partial and/or comprehensive (e. g. v_weak, moderate, . . . , extreme intensity of preference for (x, y)) OR • Comparison of intensities of preference for some pairs of reference actions – partial and/or comprehens. : (x, y) i(w, z) and/or (x, y) (w, z) MACBETH • Ordinal preference inf. w. r. t. each criterion for all not equally attractive pairs of actions: x iy or y ix, x, y A • Definition of „neutral” and „good” level on original scales of criteria • Absolute qualitative judgement of differences of attractiveness for all not equally attractive pairs of actions w. r. t. each criterion, including „good” and „neutral” points (e. g. v_weak, moderate, . . . , extreme int. pref. for (x, y)) • Ordinal preference inf. for all not equally attractive criteria: gi gj or gj gi • Absolute qualitative judgement of differences of attractiveness for all not equally attractive pairs of criteria (e. g. v_weak, moderate, . . . , extreme intensity of preference for (gi, gj)) 75

Comparison of GRIP and MACBETH cont. Preference model and final results GRIP • Uses LP to identify a set of comprehensive additive value functions with interval scales, compatible with preference info. • Builds necessary and possible weak preference relations on set A: • N (partial preorder) • P (strongly complete) • Builds necessary and possible weak preference relations on set A A: • *N (partial preorder) • *P (strongly complete) MACBETH • Uses LP to build a single interval scale for each criterion, compatible with preference info. , and computes a numerical marginal value for each action on each criterion • Computes a weight for each criterion • Builds a weighted sum model on marginal values which is additive piecewise linear or discrete • Uses the model to set up a complete preorder on set A 76

Comparison of GRIP and MACBETH n (Bana e Costa & Vansnick 1994) Summary of crucial differences in the methodology: n GRIP is using comprehensive and partial preference information on some pairs of actions n MACBETH requires partial preference information on all pairs of actions n Information about partial intensity of preference is of the same nature in GRIP and MACBETH (equivalence classes of relation i* correspond to qualitative judgements of MACBETH), but in GRIP it may not be complete n GRIP represents „disaggregation-aggregation” approach n MACBETH uses „aggregation” approach – needs weights to aggregate scales on particular criteria n GRIP works with all compatible value functions, while MACBETH builds a single interval scale for each criterion, even if many such scales would be compatible with preference information 77

Other features of GRIP n GRIP can be used interactively: n In the absence of any preference information, N, *N boil down to weak dominance relation n Each pairwise comparison or each comparison of intensities of preference *, contributes to enrich N or *N n In the absence of any preference information, P, *P is a complete relation n Each pairwise comparison or each comparison of intensities of preference *, contributes to impoverish P or *P n For complete pairwise comparisons and comparisons of intensities: N = P and *N = *P n GRIP permits to make preference intensity dependent on the part of criterion scale in which a difference of performances takes place, e. g. (17. 000; 19. 000) price (27. 000; 30. 000) 78

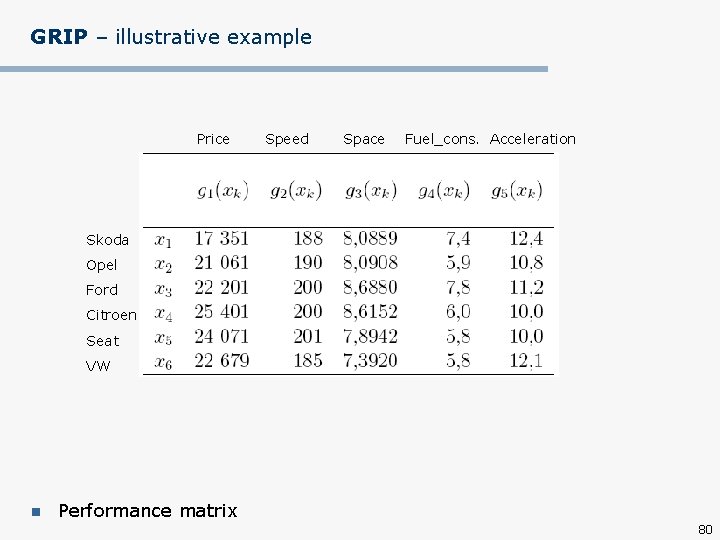
GRIP – illustrative example n Car ranking problem n Criteria: Intensity of preference: 79

GRIP – illustrative example Price Speed Space Fuel_cons. Acceleration Skoda Opel Ford Citroen Seat VW n Performance matrix 80

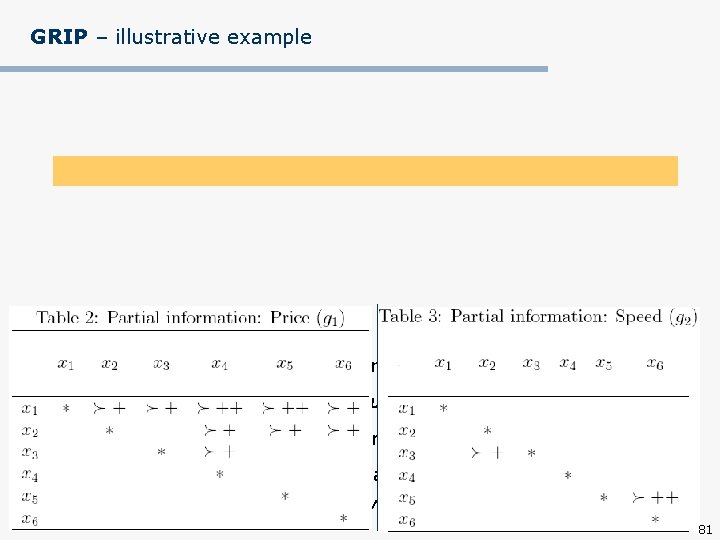
GRIP – illustrative example n Preference information n Monotonicity must be respected for each criterion, e. g. if Speed(x) Speed(y), then value[Speed(x)] value[Speed(y)] n In the ordinal regression LP problem, monotonicity is expressed by g) n In Tables 2 -6, we skip preference labels and that result from simple monotonicity, i. e. gi(x)=gi(y) or gi(x) gi(y), respectively 81

GRIP – illustrative example n Partial information about preference intensity serves to define constraints h) and j) representing partial preorder i* 82

GRIP – illustrative example (F) Skoda Opel Ford Citroen n Seat Comprehensive information about preference intensity serves to VW define constraints a) and c) representing partial preorder * 83

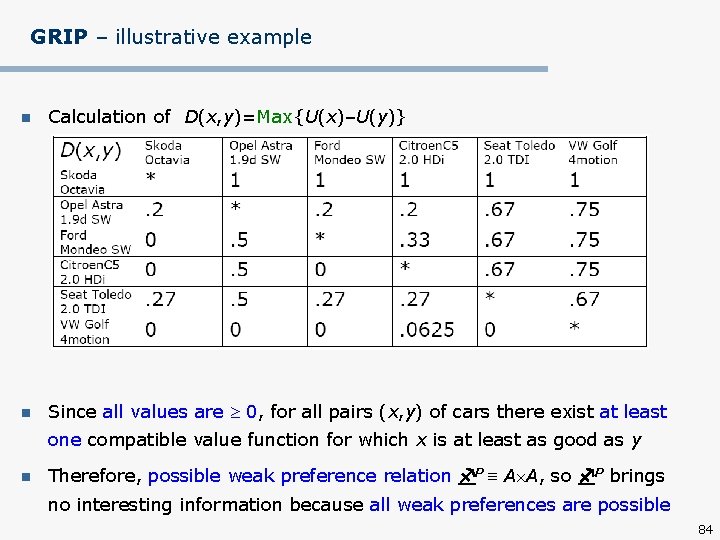
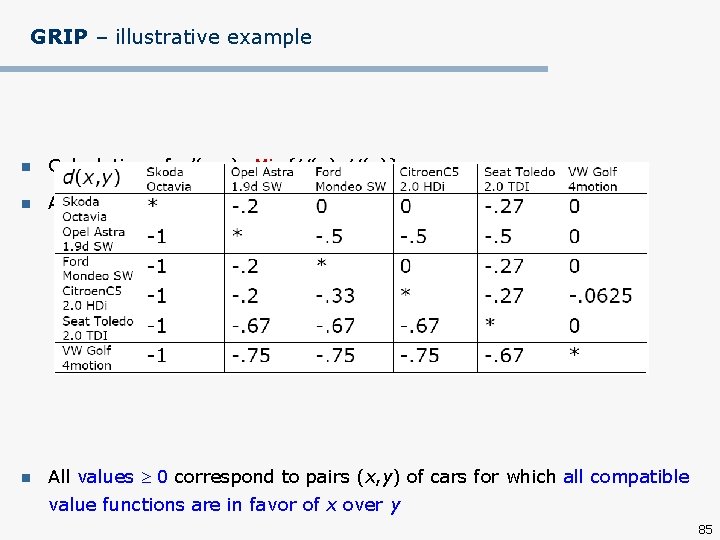
GRIP – illustrative example n Calculation of D(x, y)=Max{U(x)–U(y)} n Since all values are 0, for all pairs (x, y) of cars there exist at least one compatible value function for which x is at least as good as y n Therefore, possible weak preference relation P A A, so P brings no interesting information because all weak preferences are possible 84

GRIP – illustrative example n Calculation of d(x, y)=Min{U(x)–U(y)} n As Min{U(x)–U(y)}=–Max{U(y)–U(y)}, then d(x, y)=–D(y, x) n All values 0 correspond to pairs (x, y) of cars for which all compatible value functions are in favor of x over y 85

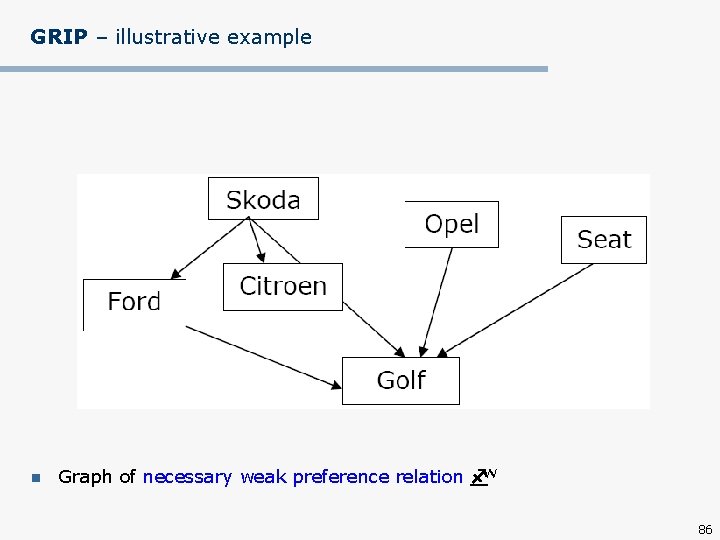
GRIP – illustrative example n Graph of necessary weak preference relation N 86

Conclusions n In GRIP, preference information is given by the DM in terms of: n partial preorder in the set of reference actions n partial and comprehensive comparisons of intensities of preference between some pairs of reference actions, n The preference information is used within regression approach to build a complete set of compatible additive value functions n Considering all compatible value functions permits to find as result: n necessary w. pref. relation in A and in A A (partial preorder) N, *N n possible w. pref. relation in A and in A A (strongly complete) P, *P n Possible extensions: n preference information with gradual credibility 87