Mthodes noyaux et SVMs Sparateurs Vastes Marges Antoine

Méthodes à noyaux et SVMs (Séparateurs à Vastes Marges) Antoine Cornuéjols Équipe TAO (INRIA/CNRS) - Université de Paris-Sud, Orsay & ENSIIE (Evry) antoine@lri. fr Cours SVM http: //www. lri. fr/~antoine

Plan 1 - Induction Méthodes à noyaux • Régression 2 - • Fonctions noyau Les SVMs Induction Méthodes à noyaux • Principe 2. 1 - Exemple de la régression • Problème associé • Illustration 2. 2 - Fonctions noyau Mise en œuvre • Validation • Construction de 3 - Exemple d’algorithme à noyau : les SVMs 4 - Mise en œuvre 5 - Bilan noyaux Bilan Cours SVM (A. Cornuéjols) 2/80

Apprentissage inductif supervisé Induction Méthodes à noyaux • Régression À partir de l’échantillon d’apprentissage S = {(xi, ui)}1, m on cherche à identifier une loi de dépendance sous-jacente • Fonctions noyau Les SVMs • Principe • Problème associé m • Illustration (fonction cible) tq : Mise en œuvre • Validation • Construction de noyaux Par exemple une fonction h aussi proche possible de f m ui = f(xi) Ou bien de la distribution de probabilités P(xi, ui) Bilan afin de prédire l’avenir Cours SVM (A. Cornuéjols) 3/80

Apprentissage inductif supervisé Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation Échantillon d’apprentissage • Construction de noyaux Bilan m Identification : h « proche de » f m Prédiction h « bonne règle de décision » Cours SVM (A. Cornuéjols) : 4/80

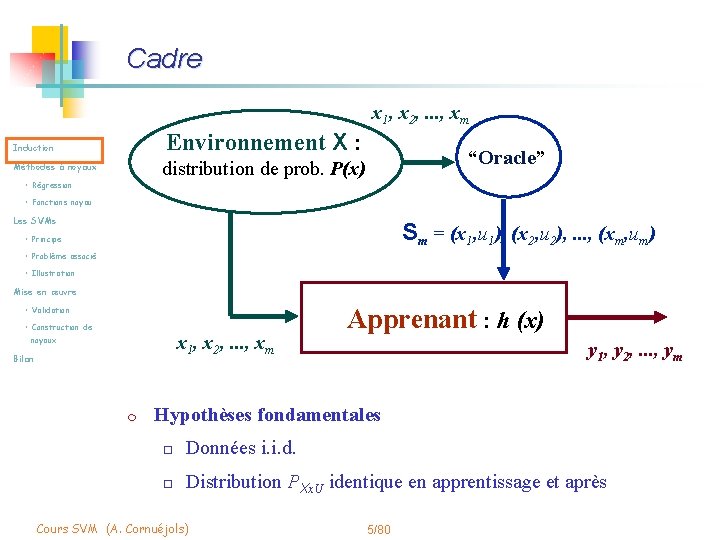
Cadre x 1, x 2, . . . , xm Environnement X : Induction “Oracle” distribution de prob. P(x) Méthodes à noyaux • Régression • Fonctions noyau Les SVMs Sm = (x 1, u 1), (x 2, u 2), . . . , (xm, um) • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de x 1, x 2, . . . , xm noyaux Bilan m Apprenant : h (x) y 1, y 2, . . . , ym Hypothèses fondamentales o Données i. i. d. o Distribution PXx. U identique en apprentissage et après Cours SVM (A. Cornuéjols) 5/80

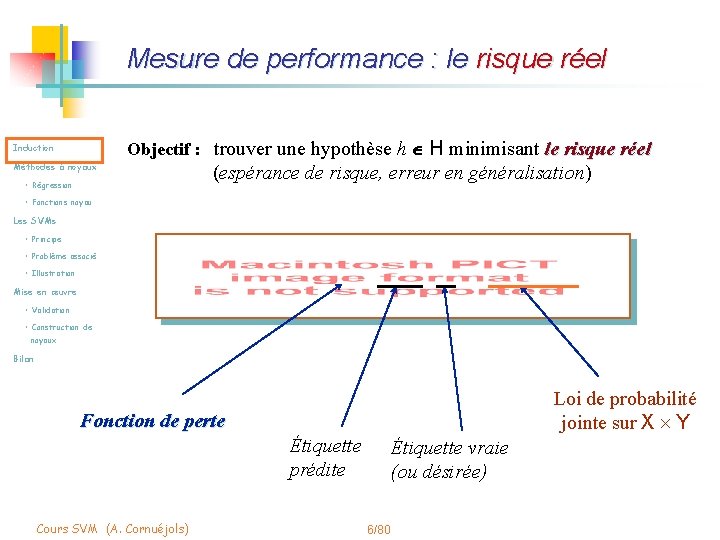
Mesure de performance : le risque réel Objectif : trouver une hypothèse h H minimisant le risque réel Induction Méthodes à noyaux • Régression (espérance de risque, erreur en généralisation) • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Loi de probabilité jointe sur X Y Fonction de perte Étiquette prédite Cours SVM (A. Cornuéjols) Étiquette vraie (ou désirée) 6/80

Le principe inductif ERM Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé m On ne connaît pas la loi de probabilité PXx. Y. m Le principe ERM (minimisation du risque empirique) prescrit de cher • Illustration Mise en œuvre • Validation • Construction de l’hypothèse h H minimisant le risque empirique noyaux Bilan Cours SVM (A. Cornuéjols) 7/80

ERM régularisé Induction Méthodes à noyaux m Pour éviter le surapprentissage ( « overfitting » ) • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 8/80

Exemple : régression linéaire Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 9/80

Approximation par moindres carrés Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Représentation duale Cours SVM (A. Cornuéjols) 10/80

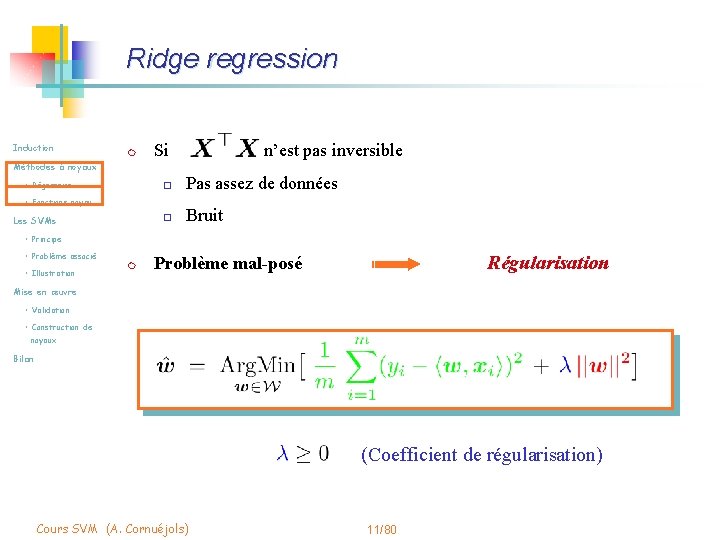
Ridge regression Induction m Méthodes à noyaux • Régression Si o Pas assez de données o Bruit • Fonctions noyau Les SVMs n’est pas inversible • Principe • Problème associé • Illustration m Régularisation Problème mal-posé Mise en œuvre • Validation • Construction de noyaux Bilan (Coefficient de régularisation) Cours SVM (A. Cornuéjols) 11/80

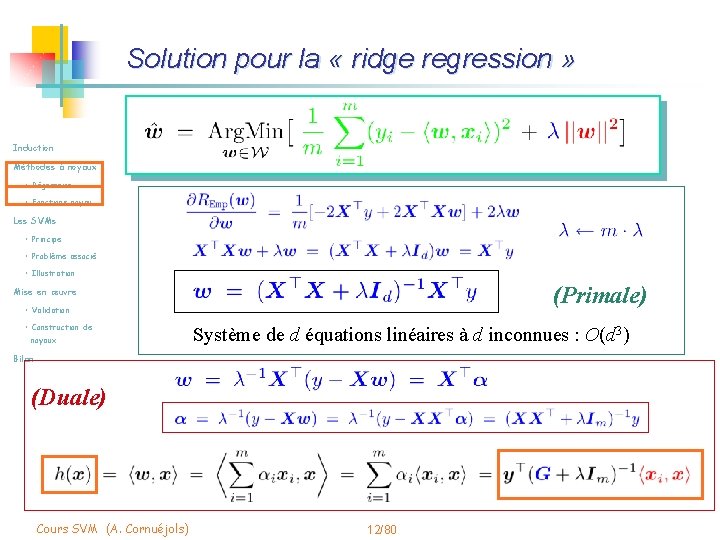
Solution pour la « ridge regression » Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration (Primale) Mise en œuvre • Validation • Construction de noyaux Système de d équations linéaires à d inconnues : O(d 3) Bilan (Duale) Cours SVM (A. Cornuéjols) 12/80

Formule duale Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs Provient directement des données • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de m noyaux Bilan L’information sur les exemples est entièrement contenue dans les produits scalaires (matrice de Gram G et les <xi , x>) m L’équation en a requiert O(m) opérations m Le calcul de h(x) requiert O(m l) opérations Cours SVM (A. Cornuéjols) 13/80

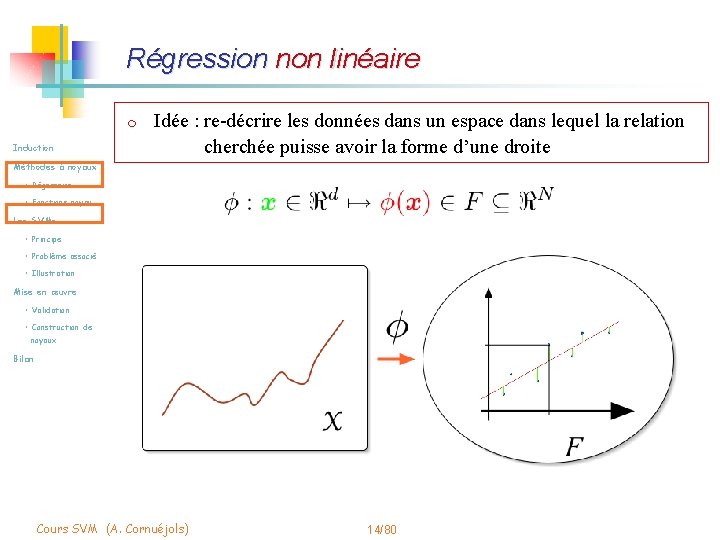
Régression non linéaire m Induction Idée : re-décrire les données dans un espace dans lequel la relation cherchée puisse avoir la forme d’une droite Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 14/80

Régression non linéaire m Induction Idée : re-décrire les données dans un espace dans lequel la relation cherchée puisse avoir la forme d’une droite Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration m Expression primale : m Expression duale : Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 15/80

Les fonctions noyau m (kernel functions) Fonction k telle que : Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Espace de redescription muni d’un produit interne où : Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 16/80

Les fonctions noyau : exemple Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux est une fonction noyau Bilan m Rq (non unicité de l’espace F défini par F) : (le même noyau calcule le produit interne dans cet espace aussi) Cours SVM (A. Cornuéjols) 17/80

Les fonctions noyau Induction Méthodes à noyaux m Efficacité computationnelle : • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 18/80

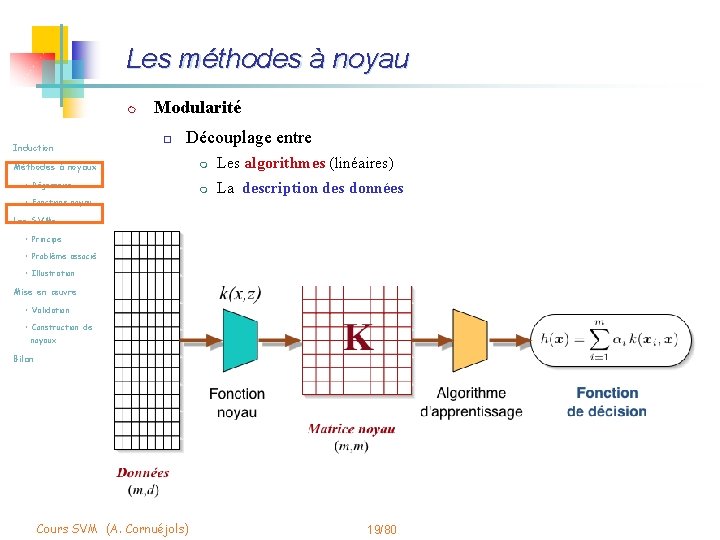
Les méthodes à noyau m Induction Modularité o Découplage entre Méthodes à noyaux • Régression • Fonctions noyau m Les algorithmes (linéaires) m La description des données Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 19/80

Petite digression … … La reconnaissance de chiffres manuscrits par réseaux de neurones (ATT Bell labs, 1993) Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 20/80

Leçons (provisoires) Induction Méthodes à noyaux L’emploi de fonctions noyau permet : • Régression • Fonctions noyau o Les SVMs D’utiliser les algorithmes de recherche de régularités linéaires pour la recherche de régularités non linéaires • Principe • Problème associé • Illustration Mise en œuvre o D’employer ces algorithmes même sur des données non vectorielles (du moment que l’on sait trouver une fonction • Validation • Construction de noyaux noyau adéquate) Bilan o De redécrire implicitement les données dans des espaces de grande dimension sans en avoir le coût computationnel Cours SVM (A. Cornuéjols) 21/80

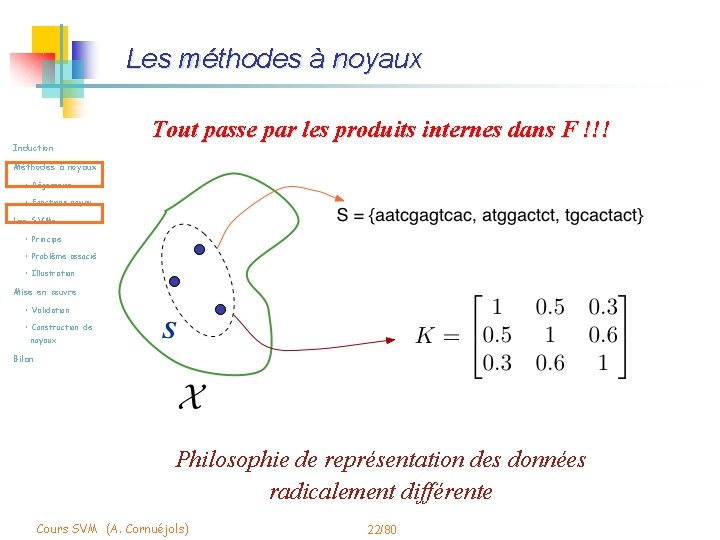
Les méthodes à noyaux Induction Tout passe par les produits internes dans F !!! Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Philosophie de représentation des données radicalement différente Cours SVM (A. Cornuéjols) 22/80

Conséquences d’une représentation par noyau Induction Méthodes à noyaux m Des informations sont perdues • Régression • Fonctions noyau o Orientation (invariance de la matrice K par rotation) o Alignement des données avec les axes (idem) Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 23/80

Les fonctions noyau : définition Induction m Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe Fonction noyau o Symétrique : o Positive définie : positive définie • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan m Théorème de Mercer o Toute fonction positive définie peut être exprimée comme un produit interne dans un espace de description Cours SVM (A. Cornuéjols) 24/80

Fonctions noyau et similarité m k(x, z) grand x similaire à z Induction Méthodes à noyaux • Régression o Évident pour le noyau gaussien : o Plus généralement : • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation Si tous les points sont de même « longueur » dans F, ( ), alors le noyau est une fonction décroissante de d. • Construction de noyaux Bilan Inversement : Cours SVM (A. Cornuéjols) 25/80

Fonctions noyau pour des vecteurs m Noyaux polynomiaux Induction Tous les produits d’exactement d variables Méthodes à noyaux • Régression • Fonctions noyau Tous les produits d’au plus d variables Les SVMs • Principe • Problème associé • Illustration Mise en œuvre m Noyaux gaussiens • Validation Sorte de décomposition en série de Fourrier • Construction de noyaux Bilan m Noyaux sigmoïdes Pas définie positive. Mais fonction de décision proche des réseaux connexionnistes Cours SVM (A. Cornuéjols) 26/80

Les SVMs (Séparateurs à Vastes Marges) m Induction Méthodes à noyaux Tâche de discrimination (entre deux classes) o Cas de la séparation linéaire • Régression • Fonctions noyau Les SVMs • Principe • Problème associé - On cherche h sous forme d’une fonction linéaire : h(x) = w. x + b - La surface de séparation est donc l’hyperplan : • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan - Elle est valide si - L’hyperplan est dit sous forme canonique lorsque ou encore Cours SVM (A. Cornuéjols) 27/80

Hyperplan de plus vaste marge Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 28/80

Optimisation de la marge Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 29/80

Optimisation de la marge m La distance d’un point à l’hyperplan est : m L’hyperplan optimal est celui pour lequel la distance aux points les plus Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs proches (marge) est maximale. Cette distance vaut • Principe • Problème associé • Illustration Mise en œuvre m Maximiser la marge revient donc à minimiser ||w|| sous contraintes: • Validation • Construction de noyaux Bilan EXPRESSION PRIMALE Cours SVM (A. Cornuéjols) 30/80

Remarques sur la justification de ce critère inductif Induction m Méthodes à noyaux Intuitivement satisfaisant o • Régression Si il y a du bruit dans les données, le séparateur à marge maximale sera plus robuste • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation m Risque empirique régularisé • Construction de noyaux Bilan o Satisfaire les données : o Régulariser : Cours SVM (A. Cornuéjols) Min ( 31/80 )

Transformation du problème d’optimisation m Méthode des multiplicateurs de Lagrange Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe EXPRESSION DUALE • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 32/80

Justification impliquant la fonction noyau m Norme du vecteur de poids m Espace d’hypothèses de norme bornée m Fonction de perte (hinge loss) m Alors : Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Complexité de Rademacher de Avec prob ≥ 1 -d Cours SVM (A. Cornuéjols) 33/80

Morale Induction Méthodes à noyaux • Régression m Les données s’expriment à travers la matrice noyau • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de m La matrice noyau contrôle la régularisation du risque noyaux Bilan Cours SVM (A. Cornuéjols) 34/80

Solution du problème d’optimisation dual Induction Méthodes à noyaux m Dans la forme duale : • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan m. S : nb de points de support Cours SVM (A. Cornuéjols) 35/80

Schéma de fonctionnement des SVMs Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 36/80

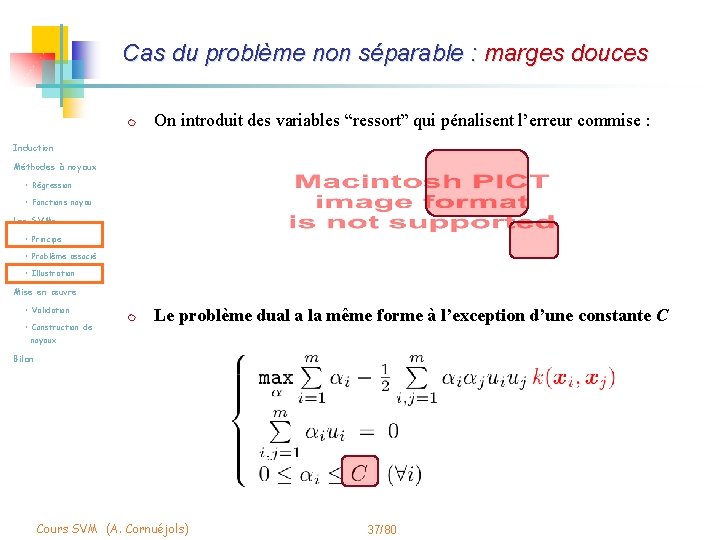
Cas du problème non séparable : marges douces m On introduit des variables “ressort” qui pénalisent l’erreur commise : m Le problème dual a la même forme à l’exception d’une constante C Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 37/80

Illustration m Induction Méthodes à noyaux Soient 5 points sur la droite : {(x 1=1, u 1 =1), (x 2=2, u 2= 2), (x 3= 4, u 3= -1), (x 4= 5, u 4 = -1), (x 5= 6, u 5= 1)} • Régression • Fonctions noyau 1 Les SVMs • Principe • Problème associé m • Illustration Mise en œuvre • Validation • Construction de 2 4 m 6 Utilisation d’un noyau polynomial de degré 2 o k(xi, xj) = (xi xj + 1)2 o C = 100 noyaux Bilan 5 Recherche de ai par : Cours SVM (A. Cornuéjols) 38/80

Illustration Induction m Méthodes à noyaux • Régression Utilisation d’un programme de résolution de problème quadratique o a 1=0, a 2=2. 5, a 3=0, a 4=7. 333, a 5=4. 833 o Les points de supports sont : { x 2=2, x 4= 5, x 5= 6} • Fonctions noyau Les SVMs • Principe • Problème associé m La fonction de décision est : • Illustration o Mise en œuvre • Validation h(x) = (2. 5)(1)(2 x+1)2 + 7. 333(1)(5 x+1)2 + 4. 833(1)(6 x+1)2+b = 0. 6667 x 2 - 5. 333 x + b • Construction de noyaux o Bilan m Avec b obtenue par h(2)=1 ou par h(5)=-1 ou par h(6)=1, puisque x 2, x 4 et x 5 sont sur la droite ui(w. TF(x)+b)=1 ce qui donne b=9 D’où : h(x) = 0. 6667 x 2 - 5. 333 x + 9 Cours SVM (A. Cornuéjols) 39/80

Illustration Valeur de la fonction discriminante Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation classe 1 classe 2 • Construction de noyaux Bilan 1 2 4 5 6 {x=2, x=5, x=6} sont points supports Cours SVM (A. Cornuéjols) 40/80

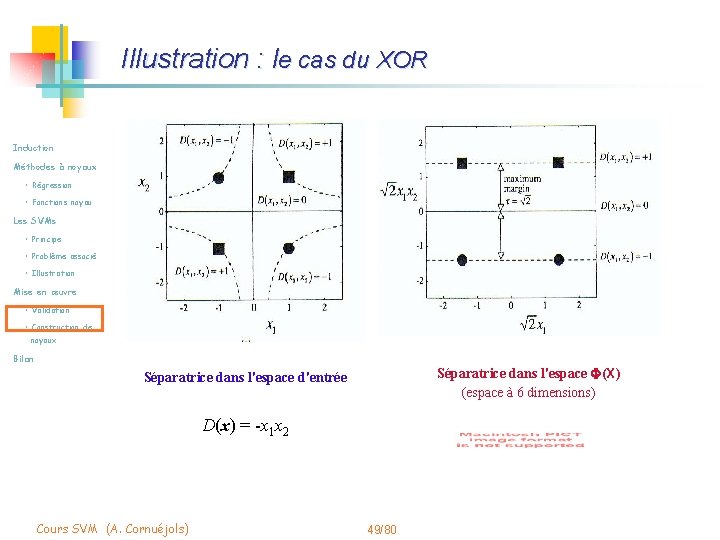
Illustration : le cas du XOR Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 41/80

Illustration : le cas du XOR Induction Fonction noyau polynomiale de d° 2 : Méthodes à noyaux • Régression K(x, x') = [1 + (x. T. x')]2 • Fonctions noyau Les SVMs • Principe • Problème associé soit : K(x, xi ) = 1 + x 12 xi 12 + 2 x 1 x 2 xi 1 xi 2 + x 22 xi 22 + 2 x 1 xi 1 + 2 x 2 xi 2 • Illustration Mise en œuvre • Validation • Construction de correspondant à la projection F : noyaux Bilan [1, x 12, √ 2 x 1 x 2, x 22, √ 2 x 1, √ 2 x 2 ] T Cours SVM (A. Cornuéjols) 42/80

Illustration : le cas du XOR Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Ici : Bilan Cours SVM (A. Cornuéjols) 43/80

Illustration : le cas du XOR m Induction Méthodes à noyaux L'optimisation de Q(a) en fonction des multiplicateurs de Lagrange conduit au système d'équations : • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan m La valeur optimale des multiplicateurs de Lagrange est : Cours SVM (A. Cornuéjols) 44/80

Illustration : le cas du XOR Induction Méthodes à noyaux • Régression m Les 4 exemples sont donc des exemples critiques ("support vectors") m La valeur optimale de Q(a) est : m Et : • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de soit : noyaux Bilan Cours SVM (A. Cornuéjols) 45/80

Illustration : le cas du XOR m Induction Méthodes à noyaux Les 4 exemples sont donc des exemples critiques ("support vectors") ( i , ai ≠ 0) • Régression • Fonctions noyau Les SVMs m La fonction de décision s’écrit : • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 46/80

Illustration : le cas du XOR En revenant dans l’espace d’origine : Induction Méthodes à noyaux Le vecteur poids optimal est : • Régression • Fonctions noyau Les SVMs • Principe • Problème associé soit : • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 47/80

Illustration : le cas du XOR Induction Méthodes à noyaux • Régression L'hyperplan optimal correspond à : • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 48/80

Illustration : le cas du XOR Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Séparatrice dans l'espace F(X) (espace à 6 dimensions) Séparatrice dans l'espace d'entrée D(x) = -x 1 x 2 Cours SVM (A. Cornuéjols) 49/80

La mise en pratique m Il faut choisir : Induction Méthodes à noyaux o Le type de fonction noyau k • Régression • Fonctions noyau Les SVMs m Sa forme m Ses paramètres • Principe • Problème associé • Illustration Mise en œuvre o • Validation La valeur de la constante C • Construction de noyaux Bilan m La sélection de ces paramètres requiert l’utilisation de méthodes empiriques pour faire le meilleur choix (validation croisée) Cours SVM (A. Cornuéjols) 50/80

Exemple : exemple + Induction Méthodes à noyaux • Régression • : exemple Dans cercle : points de support • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Fct noyau polynomiale de degré 3 Mise en œuvre • Validation • Construction de noyaux Bilan Démo : http: //svm. research. bell-labs. com/ http: //svm. dcs. rhbnc. ac. uk/pagesnew/GPat. sht ml Cours SVM (A. Cornuéjols) 51/80

Les données d'apprentissage Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 52/80

Effet des paramètres de contrôle m Apprentissage de deux classes o Induction Méthodes à noyaux • Régression • Fonctions noyau exemples tirés uniformément sur l'échiquier m SVM à fonctions noyau gaussienne m Ici deux valeurs de s Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de o En haut : petite valeur o En bas : grande valeur noyaux Bilan m Les gros points sont des exemples critiques o m Plus en haut qu'en bas Dans les deux cas : Remp = 0 Cours SVM (A. Cornuéjols) 53/80

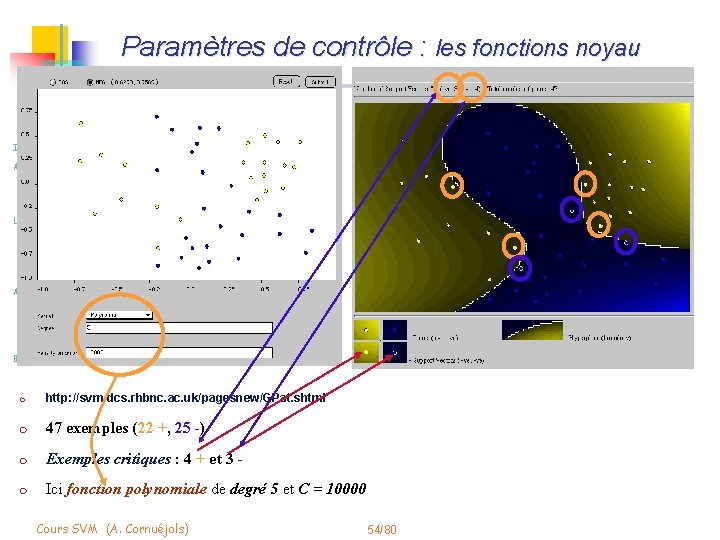
Paramètres de contrôle : les fonctions noyau Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan m http: //svm. dcs. rhbnc. ac. uk/pagesnew/GPat. shtml m 47 exemples (22 +, 25 -) m Exemples critiques : 4 + et 3 - m Ici fonction polynomiale de degré 5 et C = 10000 Cours SVM (A. Cornuéjols) 54/80

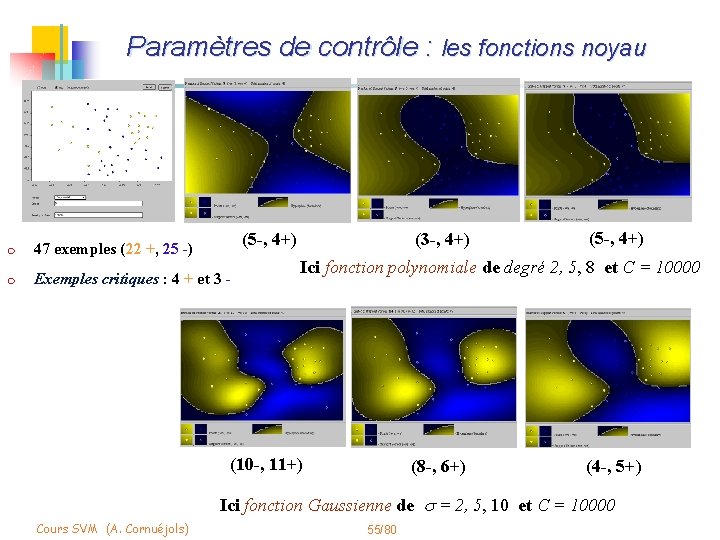
Paramètres de contrôle : les fonctions noyau Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs (5 -, 4+) • Principe m m 47 exemples (22 +, 25 -) • Problème associé • Illustration Exemples critiques : 4 + et 3 - (3 -, 4+) (5 -, 4+) Ici fonction polynomiale de degré 2, 5, 8 et C = 10000 Mise en œuvre • Validation • Construction de noyaux Bilan (10 -, 11+) (8 -, 6+) (4 -, 5+) Ici fonction Gaussienne de s = 2, 5, 10 et C = 10000 Cours SVM (A. Cornuéjols) 55/80

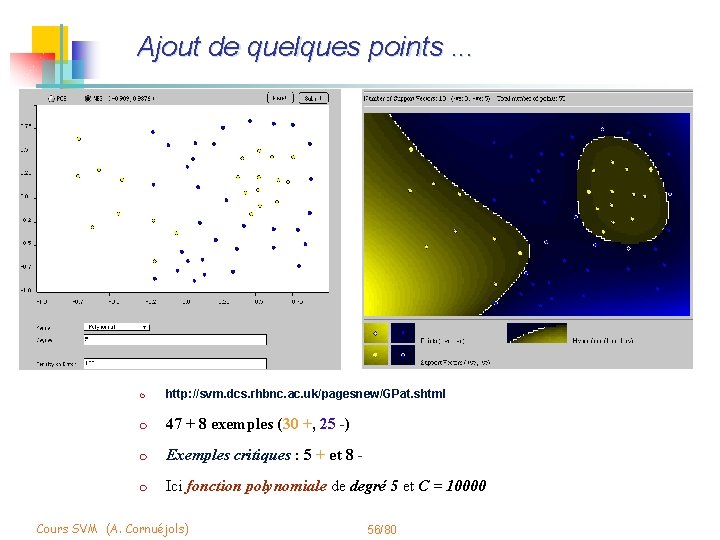
Ajout de quelques points. . . Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan m http: //svm. dcs. rhbnc. ac. uk/pagesnew/GPat. shtml m 47 + 8 exemples (30 +, 25 -) m Exemples critiques : 5 + et 8 - m Ici fonction polynomiale de degré 5 et C = 10000 Cours SVM (A. Cornuéjols) 56/80

Estimation de la performance m Empiriquement : par validation croisée m Heuristiquement (mais théoriquement fondé) Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs o Nombre de points de supports • Principe m • Problème associé • Illustration Mise en œuvre o Moins il y en a, mieux c’est Caractéristiques de la matrice noyau • Validation • Construction de m Si pas de structure dans K, aucune régularité ne peut-être trouvée m E. g. noyaux Bilan n Si les termes hors diagonale sont très petits : sur-adaptation n Si matrice uniforme : sous-apprentissage : tous les points sont attribués à la même classe Cours SVM (A. Cornuéjols) 57/80

Construction de fonctions noyau Induction m Construction à partir de fonctions noyau de base (Propriétés de clôture) Méthodes à noyaux • Régression • Fonctions noyau m Les SVMs m • Principe • Problème associé m • Illustration m Mise en œuvre • Validation • Construction de noyaux Bilan m K(x, z) = K 1(x, z) + K 2(x, z) K(x, z) = a K 1(x, z) K(x, z) = K 1(x, z). K 2(x, z) … Construction de fonctions noyau dédiées o Splines Bm o Expansion de Fourrier o Ondelettes o . . . Cours SVM (A. Cornuéjols) 58/80

Construction de noyaux Induction m Noyau invariant par translation m Noyau défini sur des ensembles Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 59/80

Stratégies de construction Induction Méthodes à noyaux m • Régression • Fonctions noyau Les SVMs • Principe • Illustration • Validation o Invariance: synonymie, longueur de document, … o Traitements linguistiques: normalisation des mots, semantique, stopwords, weighting scheme, … • Problème associé Mise en œuvre Noyau vu comme un moyen de coder de l’information a priori m Noyaux de convolution : le texte est une structure de données récursivement définie. • Construction de noyaux Pb : construire un noyau global à partir de noyaux locaux ? Bilan m Noyaux à partir de modèles génératifs : la “topologie” du problème est traduite en une fonction noyau Cours SVM (A. Cornuéjols) 60/80

Domaines d’application des SVMs m Traitement d’images Induction Méthodes à noyaux • Régression m Reconnaissance de caractères manuscrits m Reconnaissance de scènes naturelles m Reconnaissance de visages • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation o • Construction de noyaux Bilan o Entrées : image bidimensionnelle en couleur ou en niveaux de gris Sortie : Cours SVM (A. Cornuéjols) classe (chiffre / personne) 61/80

Domaines d’application des SVMs m Induction m Méthodes à noyaux • Régression • Fonctions noyau m Images : 256 * 256 (100 niveaux de gris) Codées en : 16 * 16 (niveaux de gris) + mêmes par 4 opérateurs différentiels à une dimension (|, -, /, ) = 1280 pixels (5 * 16) 25 objets pris sous 25, 89 ou 100 points de vue (ens. d’apprentissage) Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan [Thèse B. Schölkopf, 1997] Cours SVM (A. Cornuéjols) 62/80

Domaines d’application des SVMs m Résultats avec noyaux polynomiaux Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 63/80

Application : images couleurs m Base d’images Corel Stock Photo Collection m Induction Méthodes à noyaux m • Régression • Fonctions noyau m Codage Les SVMs o • Principe • Problème associé o • Illustration Mise en œuvre • Validation Pixel = vecteur dans espace à trois dimensions (RGB) Image = histogramme (fraction des pixels d’une couleur donnée) Invariant / nombreuses opérations • Construction de noyaux Bilan 200 catégories 100 images / catégorie m Noyau : (fonction c 2) Cours SVM (A. Cornuéjols) 64/80

Domaines d’application des SVMs m Catégorisation de textes Induction Méthodes à noyaux m • Régression • Fonctions noyau m Classification d’e-mails Classification de pages web Les SVMs • Principe • Problème associé • Illustration o Entrées : document (texte ou html) Mise en œuvre • Validation • Construction de noyaux m Approche « sac de mots » m Document = vecteur de mots (lemmatisés pondérés par tf-idf) o Sortie : o Noyau : Bilan Cours SVM (A. Cornuéjols) catégorie (thème, spam/non-spam) m Produit scalaire des vecteurs m C=¥ (marge dure) 65/80

Domaines d’application des SVMs m Diagnostic médical Induction Méthodes à noyaux • Régression m Évaluation du risque de cancer m Détection d’arythmie cardiaque • Fonctions noyau Les SVMs • Principe m • Problème associé • Illustration Évaluation du risque d’accidents cardio-vasculaires à moins de 6 ans Mise en œuvre • Validation • Construction de o Entrées : état du patient (sexe, age, bilan sanguin, …) o Sortie : noyaux Bilan Cours SVM (A. Cornuéjols) m Classe : à risque ou non m Probabilité d’accident à échéance donnée 66/80

Domaines d’application des SVMs Induction Méthodes à noyaux • Régression m Dans les deux cas : • Fonctions noyau Les SVMs • Principe o Pas d’information de structure o Seulement des informations globales • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 67/80

Domaines d’application des SVMs m Étude de séquences en bio-informatique Induction Méthodes à noyaux m • Régression • Fonctions noyau m Les SVMs m • Principe Biologie structurale prédictive (prédiction de structure secondaire du génome) Identification de régions codantes de l’ADN génomique Phylogénie … • Problème associé • Illustration Mise en œuvre • Validation • Construction de o Entrées : o Sortie : noyaux m Structure secondaire Intron / exon m Ancêtre m Bilan o chaînes d’acides aminées Noyau relationnel : m Cours SVM (A. Cornuéjols) Modèle génératif (chaînes de Markov : insertion, délétion, remplacement, …) 68/80

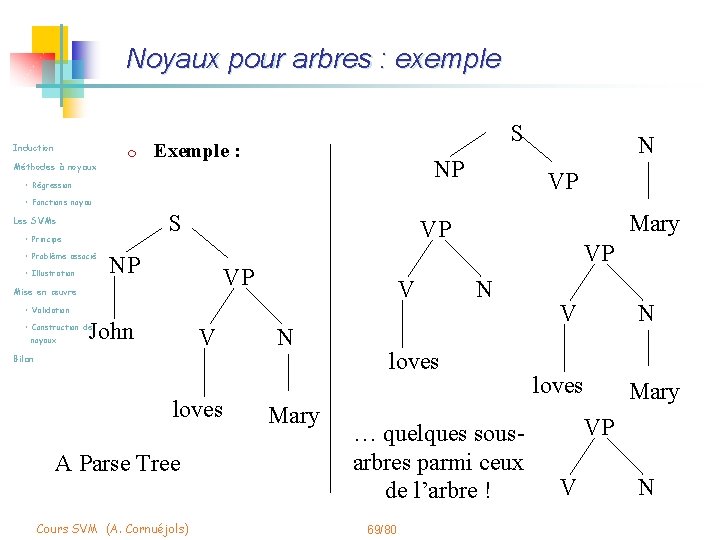
Noyaux pour arbres : exemple Induction m Méthodes à noyaux S Exemple : NP • Régression N VP • Fonctions noyau S Les SVMs • Principe • Problème associé • Illustration Mary VP NP VP Mise en œuvre V VP N • Validation John • Construction de noyaux V N Bilan loves A Parse Tree Cours SVM (A. Cornuéjols) Mary loves … quelques sousarbres parmi ceux de l’arbre ! 69/80 V N loves Mary VP V N

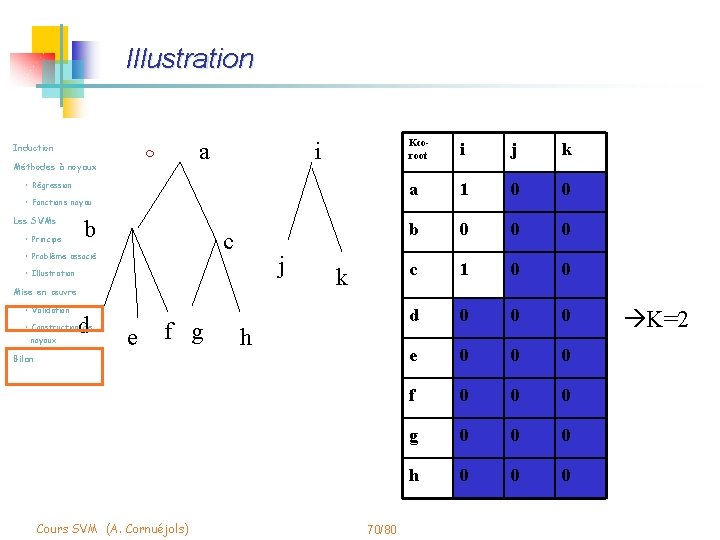
Illustration Induction a m Méthodes à noyaux i • Régression • Fonctions noyau Les SVMs • Principe b c • Problème associé j • Illustration Mise en œuvre • Validation d • Construction de noyaux e f g k h Bilan Cours SVM (A. Cornuéjols) 70/80 Kcoroot i j k a 1 0 0 b 0 0 0 c 1 0 0 d 0 0 0 e 0 0 0 f 0 0 0 g 0 0 0 h 0 0 0 K=2

Applications Induction m Méthodes à noyaux • Régression m • Fonctions noyau Les SVMs • Principe m • Problème associé • Illustration m Mise en œuvre • Validation • Construction de m noyaux Bilan m m Catégorisation de textes Reconnaissance de caractères manuscrits Détection de visages Diagnostic de cancer du sein Classification de protéines Trained SVM classifiers for pedestrian and face object detection (Papageorgiou, Oren, Osuna and Poggio, 1998) Prévision de consommation électrique Recherche de vidéos par du texte Cours SVM (A. Cornuéjols) 71/80

Implémentation des SVMs m Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs Minimisation de fonctions différentiables convexes à plusieurs variables o Pas d’optima locaux o Mais : m • Principe • Problème associé m Problèmes de stockage de la matrice noyau (si milliers d’exemples) Long dans ce cas • Illustration Mise en œuvre • Validation o D’où mise au point de méthodes spécifiques • Construction de m noyaux m Bilan o Gradient sophistiqué Méthodes itératives, optimisation par morceaux Plusieurs packages publics disponibles m m Cours SVM (A. Cornuéjols) SVMTorch SVMLight SMO … 72/80

Bilan : état des recherches m Induction Deux tâches évidentes o Méthodes à noyaux Conception de noyaux m • Régression m • Fonctions noyau Les SVMs o • Principe Noyautiser les algorithmes classiques ( « kernelization » ) • Problème associé m • Illustration m Mise en œuvre • Validation m • Construction de m noyaux m Bilan m m m Commence à être bien étudié Encore des recherches pour certains types de données SVM Kernel Régression Kernel PCA Clustering (K-means, …) Estimation de densité, détection de nouveauté Tri (ranking) … Recherche sur la sélection automatique des modèles (choix des paramètres) Cours SVM (A. Cornuéjols) 73/80

Extensions Induction Méthodes à noyaux m Classification multi-classes m Régression m Détection de « nouveautés » m Analyse en composantes principales par noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 74/80

SVM et régression m Fonction de perte : m Régression linéaire : m Soit à minimiser : m Généralisation : Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan Cours SVM (A. Cornuéjols) 75/80

SVM et apprentissage non supervisé m Détection de « nouveautés » Induction Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe • Problème associé • Illustration Mise en œuvre • Validation • Construction de noyaux Bilan On cherche à séparer au maximum le nuage de points de l’origine Cours SVM (A. Cornuéjols) 76/80

Bilan Induction m Méthodes à noyaux • Régression • Fonctions noyau Les SVMs • Principe Les méthodes à noyau sont : o Une bonne idée o Destinées à durer • Problème associé • Illustration Mise en œuvre • Validation • Construction de m Offrent une boîte à outils noyaux Bilan o Très versatile o Avec de bons fondements théoriques m Cours SVM (A. Cornuéjols) E. g. garanties de performance 77/80

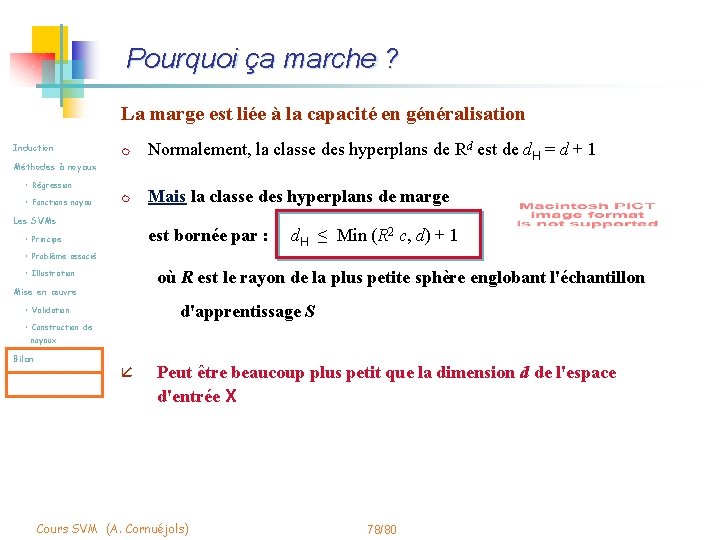
Pourquoi ça marche ? La marge est liée à la capacité en généralisation Induction m Normalement, la classe des hyperplans de Rd est de d. H = d + 1 m Mais la classe des hyperplans de marge Méthodes à noyaux • Régression • Fonctions noyau Les SVMs est bornée par : • Principe d. H ≤ Min (R 2 c, d) + 1 • Problème associé où R est le rayon de la plus petite sphère englobant l'échantillon • Illustration Mise en œuvre d'apprentissage S • Validation • Construction de noyaux Bilan å Peut être beaucoup plus petit que la dimension d de l'espace d'entrée X Cours SVM (A. Cornuéjols) 78/80

Bilan Nouvelle philosophie de représentation Induction Méthodes à noyaux m • Régression Toute l’information sur les données passe par le filtre de la matrice noyau • Fonctions noyau Les SVMs • Principe o De l’information est perdue o Permet des manipulations particulières • Problème associé • Illustration Mise en œuvre m • Validation E. g. ajout d’une constante sur la diagonale marge souple ou terme de régularisation • Construction de noyaux m Bilan o m Incorporation de connaissances a priori Matrice noyau : interface entre les modules de traitement La qualité de l’apprentissage peut être estimée à partir des caractéristiques de la matrice noyau Cours SVM (A. Cornuéjols) 79/80

Sources documentaires m Ouvrages / articles Induction o Cornuéjols & Miclet (02) : Apprentisage artificiel. Concepts et algorithmes. Eyrolles, 2002. Méthodes à noyaux o Herbrich (02) : Learning kernel classifiers. MIT Press, 2002. • Régression o • Fonctions noyau Les SVMs o • Principe • Problème associé o • Illustration Mise en œuvre o • Validation • Construction de noyaux o Bilan m Schölkopf, Burges & Smola (eds) (98) : Advances in Kernel Methods : Support Vector Learning. MIT Press, 1998. Schölkopf & Smola (02) : Learning with kernels. MIT Press, 2002. Shawe-Taylor & Cristianini(04) : Kernel methods for pattern analysis. Cambridge University Press, 2004. Smola, Bartlett, Schölkopf & Schuurmans (00) : Advances in large margin classifiers. MIT Press, 2000. Vapnik (95) : The nature of statistical learning. Springer-Verlag, 1995. Sites web o http: //www. kernel-machines. org/ (point d’entrée) o http: //www. support-vector. net (point d’entrée) Cours SVM (A. Cornuéjols) 80/80