MODELACIONES La modelacin matemtica es un intento de

MODELACIONES.

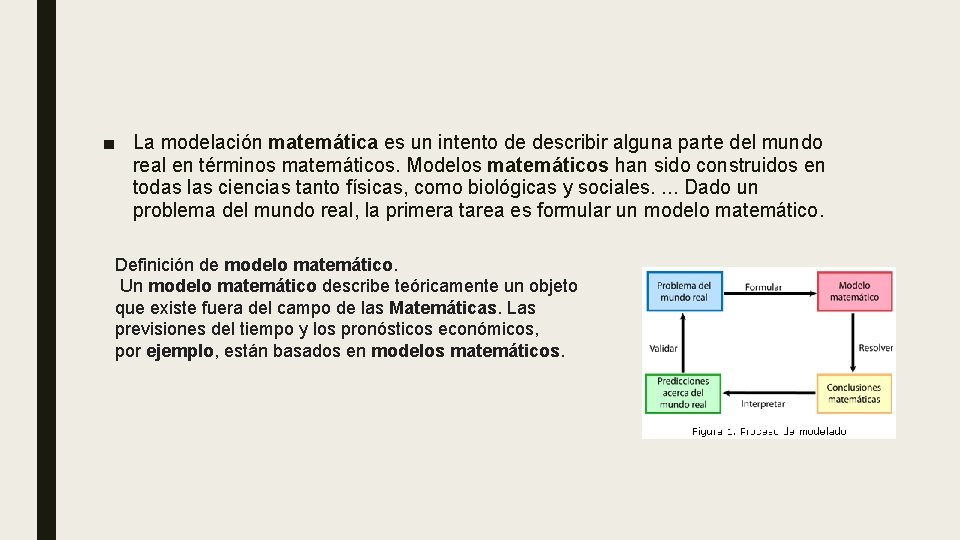
■ La modelación matemática es un intento de describir alguna parte del mundo real en términos matemáticos. Modelos matemáticos han sido construidos en todas las ciencias tanto físicas, como biológicas y sociales. . Dado un problema del mundo real, la primera tarea es formular un modelo matemático. Definición de modelo matemático. Un modelo matemático describe teóricamente un objeto que existe fuera del campo de las Matemáticas. Las previsiones del tiempo y los pronósticos económicos, por ejemplo, están basados en modelos matemáticos.

■ Un modelo matemático de un objeto (fenómeno real) es cualquier esquema simplificado e idealizado del mismo, constituido por símbolos y operaciones (relaciones) matemáticas. Un modelo matemático es un caso de formalización que emplea los más diversos instrumentos producidos en la ciencia matemática. En ciencias puras y, sobre todo, en ciencias aplicadas, se denomina modelo científico a una representación abstracta, conceptual, gráfica o visual (ver, por ejemplo: mapa conceptual), física de fenómenos, sistemas o procesos a fin de analizar, describir, explicar, simular (en general, explorar, controlar y predecir).

■ En ciencias aplicadas y en tecnología, un modelo matemático es uno de los tipos de modelos científicos que emplea algún tipo de formulismo matemático para expresar relaciones, proposiciones sustantivas de hechos, variables, parámetros, entidades y relaciones entre variables de las operaciones, para estudiar. simulación digital La simulación digital es una técnica que permite imitar (o simular) en un ordenador el comportamiento de un sistema real o hipotético según ciertas condiciones particulares de operación.

■ La Simulación Matemática es un procedimiento aplicable a una amplia gama de problemas de diversa índole en Matemática, Física, Ingeniería en general, Economía, Ciencias Sociales, etc. , desarrollado inicialmente por Enrico Fermi, John von Neumann y Stalislaw Ulam en las décadas del 30, 40 y 50 del siglo pasado.

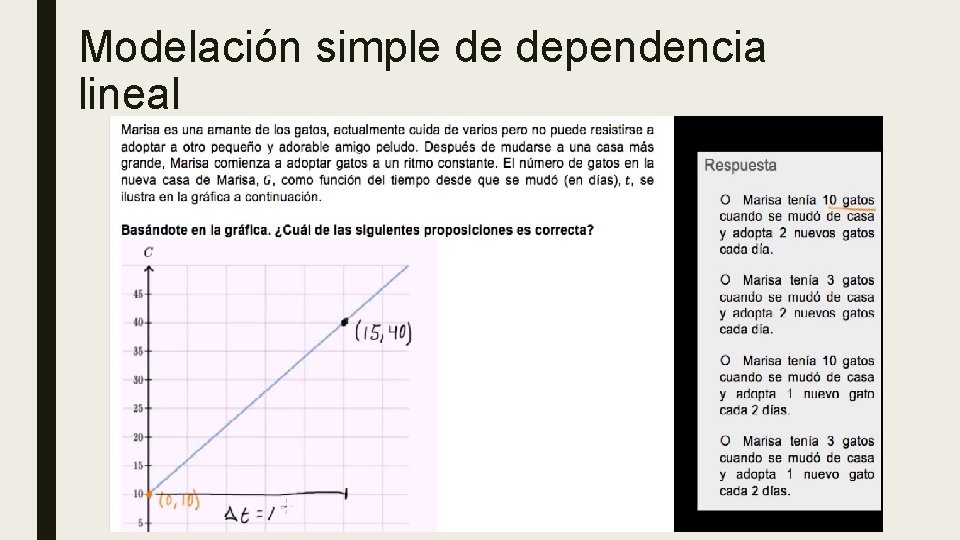
Modelación simple de dependencia lineal

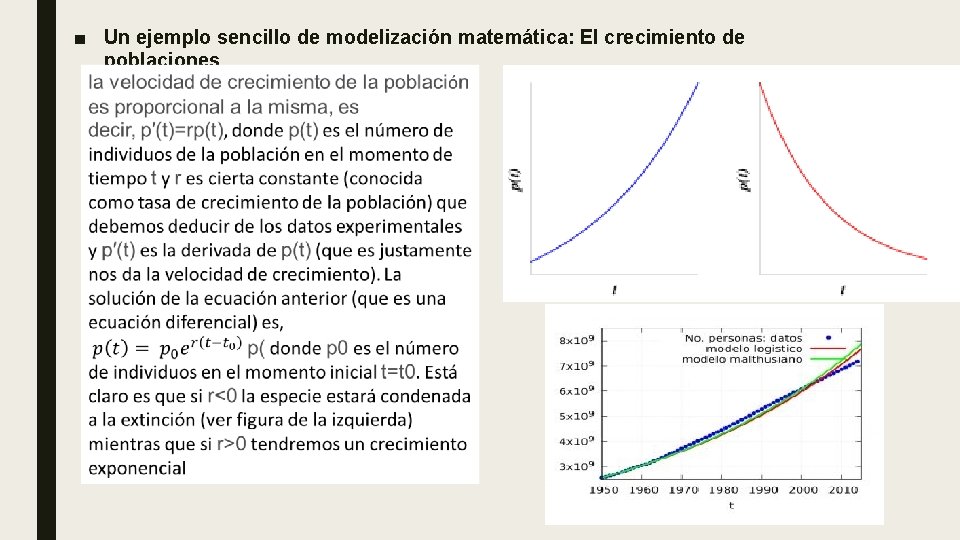
■ Un ejemplo sencillo de modelización matemática: El crecimiento de poblaciones

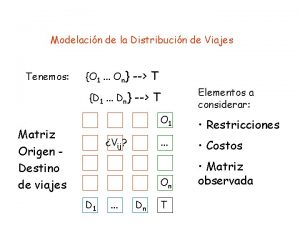
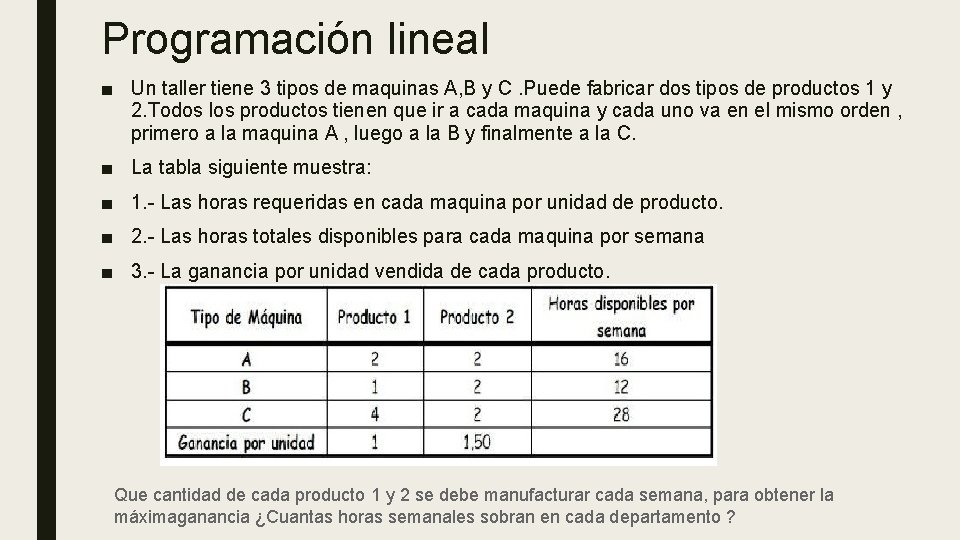
Programación lineal ■ Un taller tiene 3 tipos de maquinas A, B y C. Puede fabricar dos tipos de productos 1 y 2. Todos los productos tienen que ir a cada maquina y cada uno va en el mismo orden , primero a la maquina A , luego a la B y finalmente a la C. ■ La tabla siguiente muestra: ■ 1. - Las horas requeridas en cada maquina por unidad de producto. ■ 2. - Las horas totales disponibles para cada maquina por semana ■ 3. - La ganancia por unidad vendida de cada producto. Que cantidad de cada producto 1 y 2 se debe manufacturar cada semana, para obtener la máximaganancia ¿Cuantas horas semanales sobran en cada departamento ?

formulación ■

Problemas clásicos de aplicación. ■

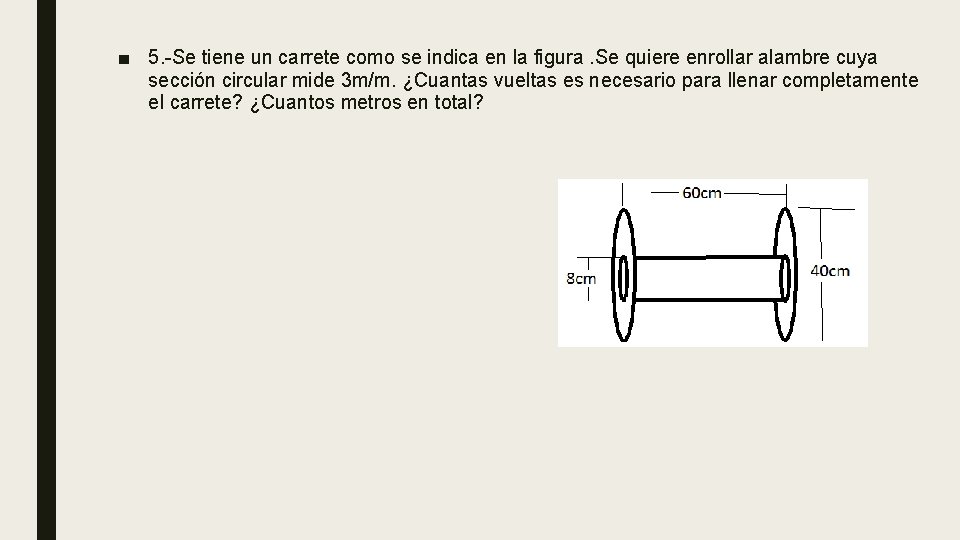
■ 5. -Se tiene un carrete como se indica en la figura. Se quiere enrollar alambre cuya sección circular mide 3 m/m. ¿Cuantas vueltas es necesario para llenar completamente el carrete? ¿Cuantos metros en total?

■ 10. -Dos ciclistas ruedan por una pista rectilínea a 60 k/h y a 40 k/h respectivamente. Cuando están separadas 1 Km. , sale una “supermosca” a una velocidad de 300 k/h en busca de la otra bicicleta, apenas toca el manubrio vuelve hacia la anterior a igual velocidad al encuentro de la otra bicicleta y continua así hasta que las dos bicicletas se encuentran. Determine: ■ 10. 1. -El tiempo en que la mosca estuvo volando. ■ 10. 2. -El camino recorrido mientras la mosca estuvo volando ■ 10. 3. - ¿Puede estimar las vueltas que la mosca estuvo volando? ■ 11. - ¿A qué hora entre las tres y las cuatro, el horario y el minutero de un reloj forman un ángulo de 90º? 12. - Las ruedas de una bicicleta tienen 60 cm. de diámetro, y un ciclista pedalea en ella dándole 50 vueltas en 8 seg. ¿Cuantos Km. recorre en dos horas?

■ 14. -Un avión vuela desde A hasta B en línea recta. Al cabo de cierto tiempo y a causa del viento contrario, el avión disminuye su velocidad hasta v Km. /h, como resultado de lo cual tarda “t”. Durante su segundo vuelo, el avión, por la misma causa, disminuye su velocidad hasta la misma magnitud, pero llega “d” Km. mas lejos que en el vuelo anterior y tarda “t’”. Hallar la velocidad inicial del avión. ■ 15. -De dos aleaciones, con diferentes porcentajes de cobre, que pesan m Kg. y n Kg. , se cortan dos pedazos de igual peso. El pedazo cortado de la primera aleación se funde con el resto de la segunda y el pedazo de la segunda aleación se funde con la primera, después de lo cual, el porcentaje de cobre en ambas aleaciones se hace igual. ¿Cuánto pesa cada uno de los pedazos cortados? ■ 16. -Manuel y Diego, trabajando juntos pintan un edificio en 10 días. Si Manuel trabajara solo durante 3 días y, a continuación, Diego trabajara solo durante 4 días harían solo la tercera parte del trabajo. ¿Cuánto demoraría, cada uno por separado, en realizar el trabajo?

■ 17. -Las dimensiones de un paralelepípedo están en la razón 6: 9: 12, Si el lado mayor se disminuye en un 30%, y el lado mayor se aumenta en un 40%. Determine. ■ 17. 1. - ¿En qué porcentaje aumenta la superficie total del paralelepípedo? ■ 17. 2. - ¿En qué porcentaje aumenta el volumen del paralelepípedo? ■ 18. - Deduzca, geométricamente los principales productos notables. ■ 19. - Si la superficie de un cuadrado se aumenta en un 50%, ¿En cuánto aumenta su diagonal? ¿En qué % aumenta el área? ■ 20. - Se tiene un triangulo rectángulo cuyos ángulos agudos están en la razón 2: 1, . El cateto menor mide 6 cm. Sobre la hipotenusa se construye un nuevo triangulo semejante con el primero y así sucesivamente. Determine la hipotenusa del sexto triangulo construido de esta manera.

■ 21. - En un cuadrado de lado “a”, se inscribe una circunferencia, luego sobre esta circunferencia se inscribe un círculo, luego sobre esta ultima un nuevo cuadrado y así sucesivamente hasta completar cinco círculos en la serie. ■ Determine: ■ 21. 1. -La suma de las superficie de todos los cuadrados construidos de este modo. 21. 2. -La suma de las superficies de todos los círculos construidos de este modo. ■ 22. - En un triangulo equilátero de lado L , sobre la mitad de cada uno ■ de los lados se construye un nuevo triangulo y sobre este otro mas. ■ Si este proceso se repite indefinidamente. Encontrar una relación ■ matemática para calcular: ■ 22. 1. - La suma de las áreas de los infinitos triángulos así obtenidos. ■ 22. 2. -La suma de los perímetros de los infinitos triángulos así construidos.

■ 23. - Cercado de una cancha de futbol. Una cancha de fútbol de 25 metros de ancho por 76 de largo se va a cercar dejando un espacio o corredor entre la cerca y el borde del área de juego. El costo de la cerca es de Bs. 4. 000 por metro lineal. Si se dispone de Bs. 968. 000 para cercar la cancha, entonces calcular el ancho del corredor. ■

Solución ■ Sea X el ancho del corredor. ■ Entonces el perímetro del rectángulo a cercar es P = 2(76 + 2 X) + 2(25 + 2 X) ■ El costo total de la cerca es igual a este perímetro por el costo de cada metro de cerca. ■ Luego se tiene la relación de costo 400 · ((76 + 2 X) + 2(25 + 2 X)) = 968. 000 (76 + 2 X) + (25 + 2 X) = 121 de donde 4 X = 20 ■ luego X = 5. Por lo tanto el ancho del corredor debe ser de 5 metros

■ 24. -Calculo de Edades. Pármeno es 5 años mayor que Sempronio. Hace diez años, la suma de las dos edades era igual a 35. ¿Cuál es la edad actual de cada uno de ellos? ■

■ Solución. Sea X la edad actual de Sempronio. ■ Entonces X + 5 es la edad actual de Pármeno. ■ La suma de las dos edades hace 10 años fue (X − 10) + (X − 5) = 35 ■ de donde 2 X = 50 ■ X = 25 Luego la edad de Sempronio es 25 y la de Pármeno es 30.

■ 25. -Fabricación de Ron. Un fabricante de Ron ■ desea producir 60. 000 lt. de un Ron Especial ■ con un grado alcohólico de 26 %. Si dispone de ■ un Ron Añejo de 30 % de grado alcohólico y ■ otro de 20. 5 % ¿Qué cantidad de cada ron ■ deberá mezclar para obtener la cantidad ■ deseada del Ron Especial? ■ ■

■ Solución. Sea X la cantidad del primer tipo de ron a usar en la mezcla. ■ Luego 60. 000 - X será la cantidad a usar del segundo ron. ■ Luego la concentración de alcohol será ■ X · 30 100 + (60. 000 − X) · 20. 5 100 = 60. 000 · 26 100 ■ Después de multiplicar por 100 en todas partes, ■ obtenemos 30 X + 1320000 − 20. 5 X = 1560000 ■ o sea 9. 5 X = 240. 000 ■ de donde se concluye que X = 25263 ■ Luego se deben mezclar 25263 litros del primer ron y 24737 litros del segundo

■ 26. -Número Natural. Un número elevado al cubo, menos el cuadrado del mismo más el número es igual 105. Calcular dicho número. ■

■ Solución. ■ Sea x el número. Entonces x 3 − x 2 + x = 105 ■ Por lo tanto se tiene una ecuación polinomial P(x) = x 3 − x 2 + x − 105 = 0 ■ Este polinomio se factoriza, mediante el método de Ruffini ■ como P(x) = (x − 5)(x 2 + 4 x + 21) ■ Luego x = 5 es el número buscado.

■ 27. -Pintura de una puerta. Una puerta de 2. 15 m de alto por 0. 8 m de alto y 3 cm. de espesor se pintó con un barniz. Si el espesor de la capa de barniz es de 0. 2 mm. ¿Qué volumen de pintura se utilizó? ■ ■.

■ Solución. Sea S la superficie de la puerta. Entonces el volumen V de pintura usada es igual a V = S · 0. 2 mm

■ Solución. Sea C el costo del material en Bs. y S la superficie del balón. Entonces C = 5. 000 · S · grosor C = 5. 000 Bs/m 3 · 4π(0. 15 m) 2 · 2. 6 · 10− 3 m. C = 3. 67 Bs.

■ Solución. ■ Sea V el volumen de la viga y P el peso en Kgs. ■ Entonces P = V · ρ = π(0. 015 m) 2 · (12 m)(7. 86 · 103 Kg/m 3 ) ■ P = 66. 6 Kg ■ Luego el peso de la viga es de 66. 6 Kilogramos.

■ 30. -Velocidad promedio de un automóvil. Un automóvil recorrió 250 Km. a una velocidad promedio de 70 Km/h. Si los primeros 50 Km. los recorrió a 606 Capitulo 1. Problemas de Ciencia Km/h ¿Qué velocidad promedio debe desarrollar en el resto del trayecto? ■

■ Solución Sea v la velocidad promedio empleada en recorrer los 200 Km. faltantes. Entonces la velocidad promedio en todo el trayecto se expresa 50 250 · 60 Km/h + 200 250 v = 70 Km/h Luego 200 250 v = 70 Km/h − 12 Km/h = 58 Km/h de donde v = 250 · 58 Km/h 200 = 72. 5 Km/h Luego el automóvil debe desplazarse a una velocidad promedio de 72. 5 Km/h durante el resto del trayecto. 12. ■

■ Solución. ■ Sea X el tiempo empleado por la válvula A en verter agua dentro de la piscina. Luego 2 X será el tiempo empleado por la otra válvula. ■ Entonces la capacidad de la piscina viene dada por 50 lt/s · X + 75 lt/s · ■ 2 X = 450. 000 lt. 200 · Xlt/s = 450. 000 lt. de donde X = 2250 s ■ Luego la válvula A estuvo abierta durante 2250 segundos = 37. 5 minutos, mientras que la válvula B permaneció abierta por 7

■ 32. Punto de encuentro en la carretera. Un auto sale de una ciudad A hacia otra ciudad B, que se encuentra 1. 2. Problemas de Movimiento 7 a 250 Km. de A, desplazándose en línea recta y a una velocidad constante de 90 Km/h. Cinco minutos más tarde, un segundo auto sale de B, desplazándose hacia A una velocidad de 95 Km/h ¿ En qué punto de la carretera se encuentran los dos vehículos ?

■ Solución. Sea X la distancia en Kms recorrida por el primer auto, desde A hasta el lugar de encuentro. ■ El tiempo necesario, en horas, para recorrer X Kms. es t 1 = X 90 ■ Por otro lado, el tiempo en horas que tarda el segundo vehículo es ■ t 2 = 250 − X 95 + 5 60 donde el primer sumando representa el tiempo en movimiento y 5/60 representa el tiempo que permaneció el auto parado. ■ Como ambos tiempos deben ser iguales, se tiene X 90 = 250 − X 95 + 1 12 ■ de donde 1140 X = 90(3000 − 12 X + 95), 2220 X = 278550 ■ con lo cual X = 278550 2220 = 125. 47 Km. ■ Luego los dos autos se encuentran a 125. 47 Km. de la ciudad A, en la dirección de B.

■ 33. Distancia recorrida. Una camioneta viaja en línea recta, con una velocidad constante de 100 Km/h durante una hora y 25 minutos hasta detenerse por completo. Luego se regresa al lugar de partida a una velocidad de 70 Km/h y se detiene a descansar después de haber viajado durante una hora ¿A qué distancia se halla del punto de partida?

■ Solución. Sea d 1 la distancia desde el punto de partida hasta la llegada. Entonces este se calcula d 1 = 100 Km/h · 1. 4166 h = 141. 66 Km 8 capítulo 1. Problemas de Ciencia Sea d 2 la distancia recorrida al regresar. Luego d 2 = 70 Km · 1 h = 70 Km. Luego la distancia desde el punto de partida hasta el punto de descanso será la diferencia entre ambas distancias y por lo tanto d = d 1 − d 2 = 141. 66 Km − 70 Km = 71. 66 Km

■ ■ 34. Velocidad de caída. Una pelota se deja caer desde un edificio de 52 metros de altura ¿Con que velocidad choca contra el piso? ¿Cuánto tiempo tarda en caer?

■ Solución. La velocidad v de caída satisface la ecuación de movimiento v 2 = 2 · g · h donde g = 9. 8 m/sg 2 es la aceleración de la gravedad y h es la distancia recorrida por la pelota. Luego v = p 2 · g · h = q 2 · 9. 8 m/sg 2 · 52 m v = 22. 13 m. Para calcular el tiempo en caer al suelo usamos la relación h = 1 2 · g · t 2 o sea t = s 2 · h g = s 2 · 52 m 9. 8 m/sg 2 t = 3. 2 sg. Luego la pelota tarda 3. 2 segundos en caer al suelo

■ 35. Caída con velocidad inicial. Si en el problema anterior la pelota se lanza hacia abajo con una velocidad de 20 m/s ¿Con que velocidad choca contra el piso ? ¿Cuánto tiempo tarda en caer? ■

■ 36. -Problemas de Astronomía. La Astronomía es una de las ramas más emocionantes de las ciencias y también una de las más antiguas. Podemos calcular la distancia entre los planetas y el sol, el diámetro, su masa, . . Usando las Leyes de Gravitación Universal. 1. Fuerza de gravedad en el Planeta Marte. Calcular la fuerza de gravedad en el Planeta Marte sabiendo que su diámetro es 6. 798 Km. y su masa es 0. 107 la masa de la tierra.

■ Solución. Sea g la fuerza de gravedad en Marte. Entonces de acuerdo a la Ley de Gravitación Universal, la fuerza de gravedad viene dada por g = G · M R 210 capítulo 1. Problemas de Ciencia donde G = 6. 67 x 10− 11 Newton · m 2/Kg 2 es la constante de gravitación Universal, M es la masa del planeta y R su radio. Recordemos además que 1 Newton = 1 Kg · m/sg 2. Masa de la Tierra = 6 · 1024 Kg. Por lo tanto g = 6. 67 x 10− 11 Newton · m 2 · 0. 107 · 6 · 1024 (6. 798. 000 m/2)2 Kg˙ 2 Después de cancelar algunas unidades y multiplicar potencias de 10 nos queda g = 6. 670˙. 107 · 6 · 1013 (3. 399)2 · 1012 m/sg 2 Cancelando potencias de 10 produce g = 6. 671˙. 07 · 6 (3. 399)2 m/sg 2 = 3. 706 m/sg 2 Luego la fuerza de gravedad en el planeta Marte es 3. 706 m/sg 2.

■ 37. - El Planeta Kraptón En un planeta cuya fuerza de gravedad sea la décima parte que la de la tierra, una persona puede saltar varios metros de altura fácilmente e inclusive volar un poquito como Superman. ¿Qué radio debe tener un planeta con la misma masa de la tierra para que su fuerza de gravedad sea 10 veces menor que la de la tierra?

■ Solución. Sea g la gravedad de Kraptón. Entonces g = 9. 8 m/sg 2 10 = 0. 98 m/sg 2 Usamos la ley de gravitación Universal para hallar el radio del planeta. En efecto tenemos g = G · M R 2 de donde R = s M · G g = s 6. 67 · 10− 11 Newton · 6 · 1024 Kg 0. 98 m/sg 2 Después de cancelar algunas unidades y hacer operaciones nos queda R = √ 40. 836 · 1013 m. = 20208 Km. Luego el Planeta Kraptón deberá tener un radio de 20208 Km. La relación entre el volumen de Kraptón y el de la tierra es de 31. 92. Luego Kraptón es casi 32 veces más grande que nuestro planeta y tiene la misma masa. De aquí se concluye que 12 capítulo 1. Problemas de Ciencia hay muchos agujeros en Kraptón dentro de los cuales pudieron construirse ciudades maravillosas.

■ Gracias ■ Montoya. -