Markov Decision Processes Lirong Xia Today Markov decision

Markov Decision Processes Lirong Xia

Today ØMarkov decision processes • search with uncertain moves and “infinite” space ØComputing optimal policy • value iteration • policy iteration 1

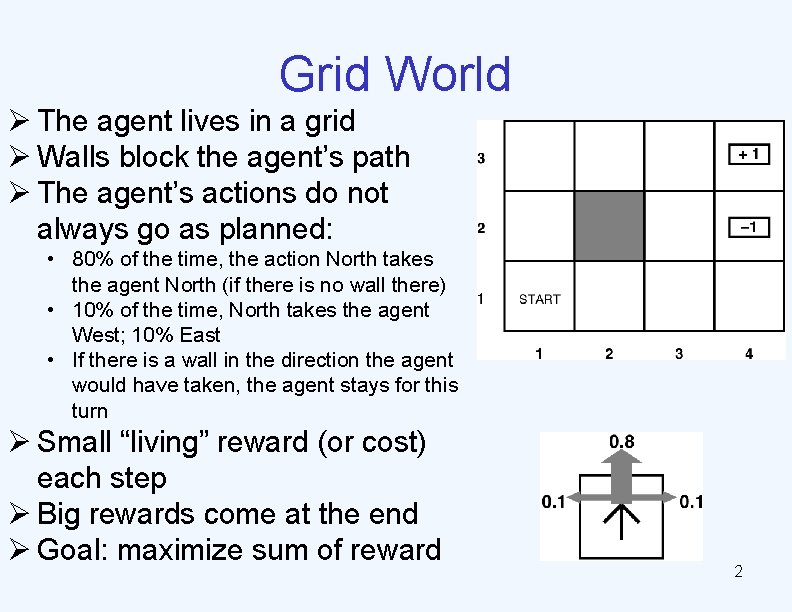
Grid World Ø The agent lives in a grid Ø Walls block the agent’s path Ø The agent’s actions do not always go as planned: • 80% of the time, the action North takes the agent North (if there is no wall there) • 10% of the time, North takes the agent West; 10% East • If there is a wall in the direction the agent would have taken, the agent stays for this turn Ø Small “living” reward (or cost) each step Ø Big rewards come at the end Ø Goal: maximize sum of reward 2

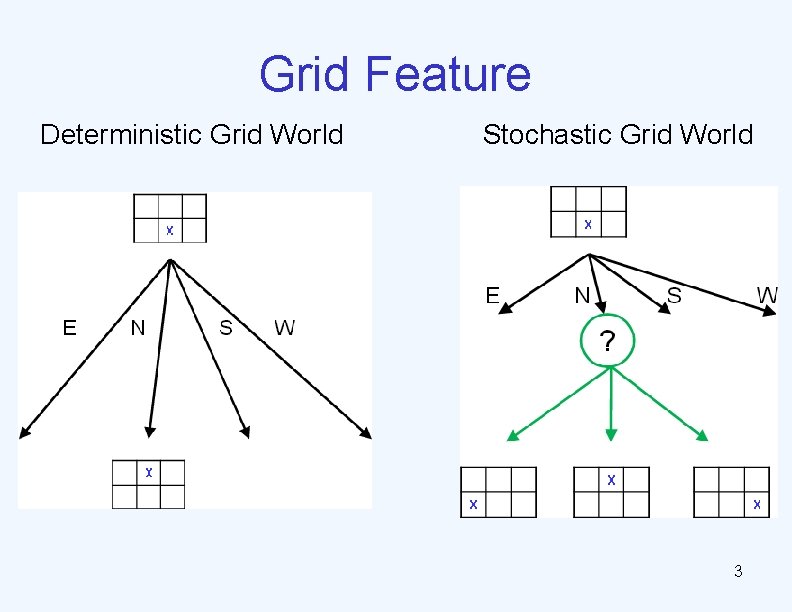
Grid Feature Deterministic Grid World Stochastic Grid World 3

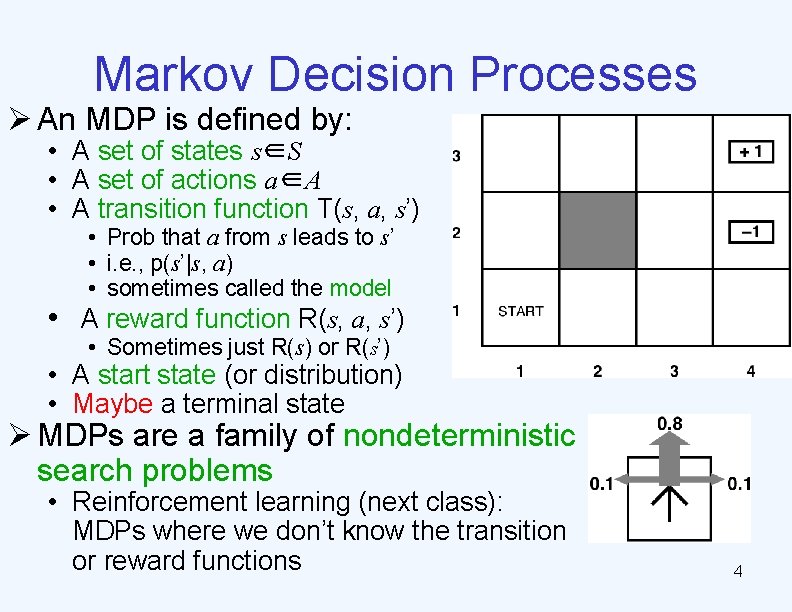
Markov Decision Processes Ø An MDP is defined by: • A set of states s∈S • A set of actions a∈A • A transition function T(s, a, s’) • Prob that a from s leads to s’ • i. e. , p(s’|s, a) • sometimes called the model • A reward function R(s, a, s’) • Sometimes just R(s) or R(s’) • A start state (or distribution) • Maybe a terminal state Ø MDPs are a family of nondeterministic search problems • Reinforcement learning (next class): MDPs where we don’t know the transition or reward functions 4

What is Markov about MDPs? Ø Andrey Markov (1856 -1922) Ø “Markov” generally means that given the present state, the future and the past are independent Ø For Markov decision processes, “Markov” means: 5

Solving MDPs Ø In deterministic single-agent search problems, want an optimal plan, or sequence of actions, from start to a goal Ø In an MDP, we want an optimal policy • A policy π gives an action for each state • An optimal policy maximizes expected utility if followed Optimal policy when R(s, a, s’) = -0. 03 for all nonterminal state 6

Plan vs. Policy ØPlan • A path from the start to a GOAL ØPolicy • a collection of optimal actions, one for each state of the world • you can start at any state 7

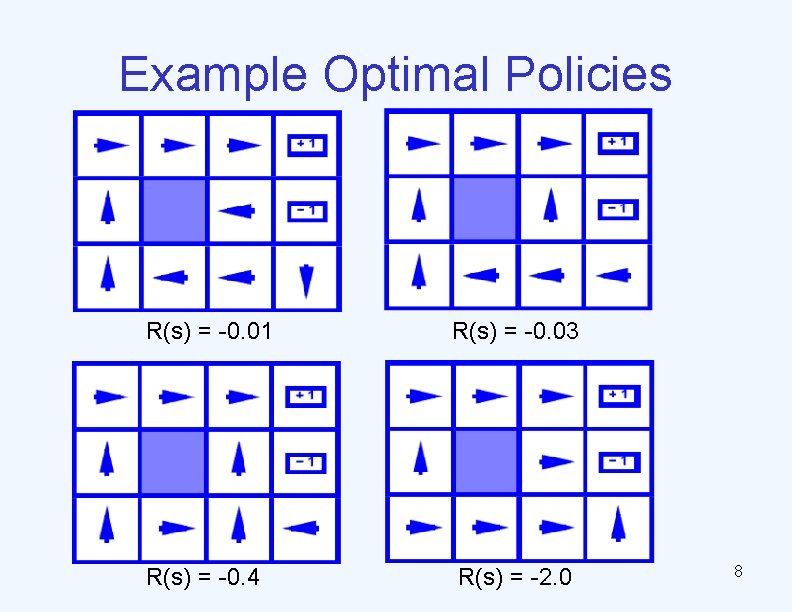
Example Optimal Policies R(s) = -0. 01 R(s) = -0. 03 R(s) = -0. 4 R(s) = -2. 0 8

Example: High-Low Ø Three card type: 2, 3, 4 Ø Infinite deck, twice as many 2’s Ø Start with 3 showing Ø After each card, you say “high” or “low” Ø If you’re right, you win the points shown on the new card Ø If tied, then skip this round Ø If you’re wrong, game ends Ø Why not use expectimax? • #1: get rewards as you go • #2: you might play forever! 9

High-Low as an MDP Ø States: 2, 3, 4, done Ø Actions: High, Low Ø Model: T(s, a, s’): • • • p(s’=4|4, low) = ¼ p(s’=3|4, low) = ¼ p(s’=2|4, low) = ½ p(s’=done|4, low) =0 p(s’=4|4, high) = ¼ p(s’=3|4, high) = 0 p(s’=2|4, high) = 0 p(s’=done|4, high) = ¾ … Ø Rewards: R(s, a, s’): • Number shown on s’ if • 0 otherwise Ø Start: 3 10

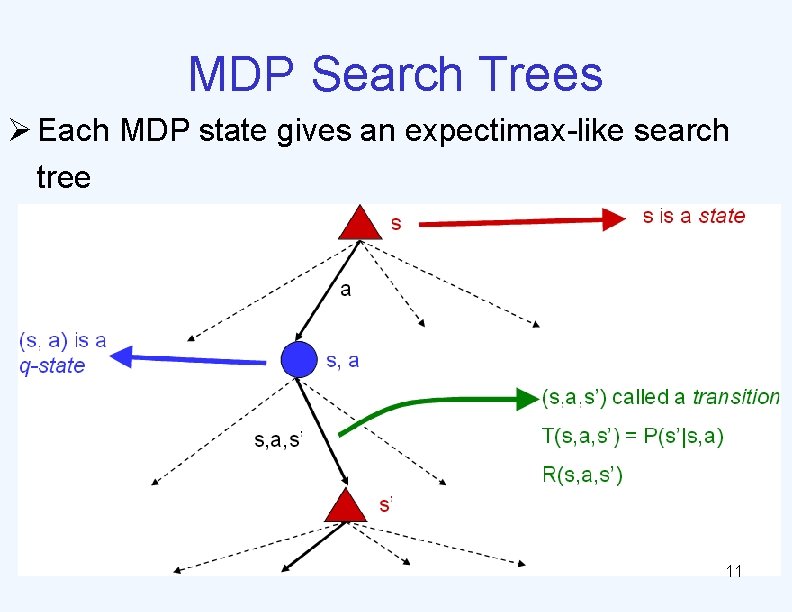
MDP Search Trees Ø Each MDP state gives an expectimax-like search tree 11

Utilities of Sequences Ø In order to formalize optimality of a policy, need to understand utilities of sequences of rewards Ø Typically consider stationary preferences: Ø Two coherent ways to define stationary utilities • Additive utility: • Discounted utility: 12

Infinite Utilities? ! Ø Problems: infinite state sequences have infinite rewards Ø Solutions: • Finite horizon: • Terminate episodes after a fixed T steps (e. g. life) • Gives nonstationary policies (π depends on time left) • Absorbing state: guarantee that for every policy, a terminal state will eventually be reached (like “done” for High-Low) • Discounting: for 0<ϒ<1 • Smaller ϒ means smaller “horizon”-shorter term focus 13

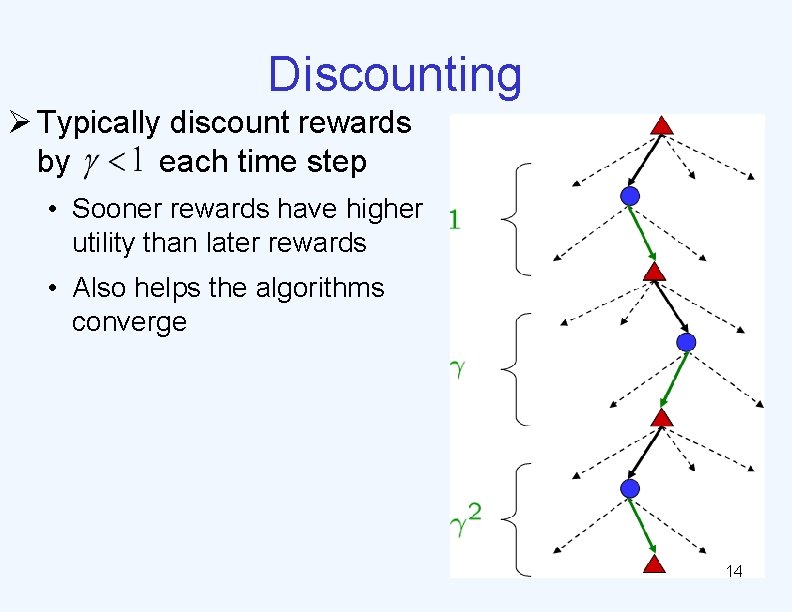
Discounting Ø Typically discount rewards by each time step • Sooner rewards have higher utility than later rewards • Also helps the algorithms converge 14

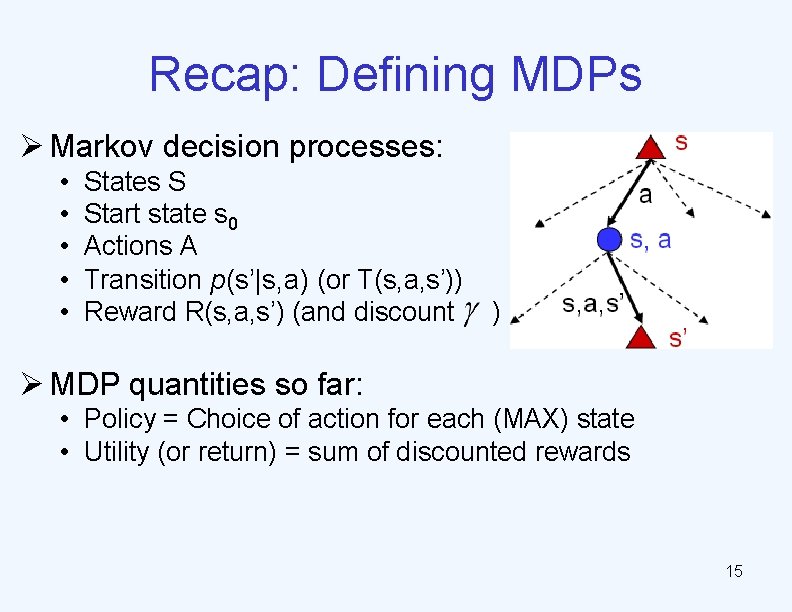
Recap: Defining MDPs Ø Markov decision processes: • • • States S Start state s 0 Actions A Transition p(s’|s, a) (or T(s, a, s’)) Reward R(s, a, s’) (and discount ) Ø MDP quantities so far: • Policy = Choice of action for each (MAX) state • Utility (or return) = sum of discounted rewards 15

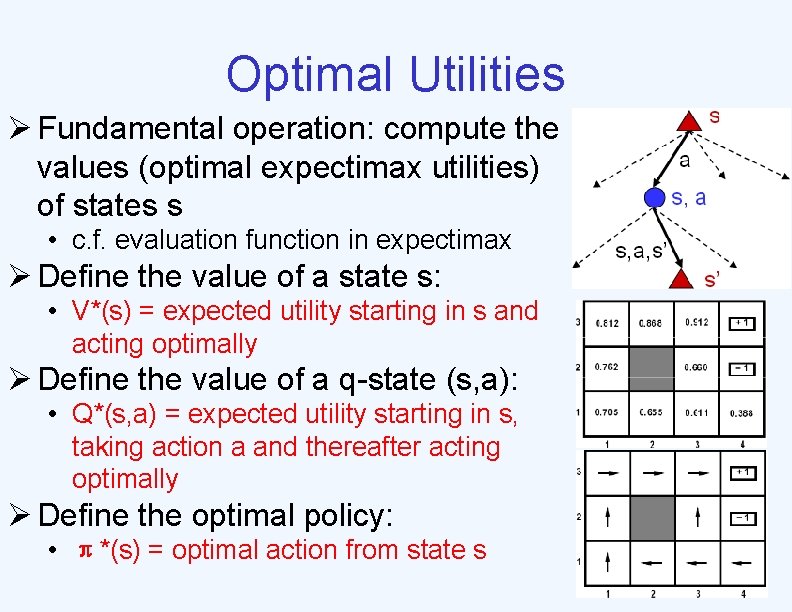
Optimal Utilities Ø Fundamental operation: compute the values (optimal expectimax utilities) of states s • c. f. evaluation function in expectimax Ø Define the value of a state s: • V*(s) = expected utility starting in s and acting optimally Ø Define the value of a q-state (s, a): • Q*(s, a) = expected utility starting in s, taking action a and thereafter acting optimally Ø Define the optimal policy: • π*(s) = optimal action from state s

The Bellman Equations Ø Definition of “optimal utility” leads to a simple one-step lookahead relationship amongst optimal utility values: Optimal rewards = maximize over first step + value of following the optimal policy Ø Formally: 17

Solving MDPs Ø We want to find the optimal policy Ø Proposal 1: modified expectimax search, starting from each state s: 18

Why Not Search Trees? Ø Why not solve with expectimax? Ø Problems: • This tree is usually infinite • Same states appear over and over • We would search once per state Ø Idea: value iteration • Compute optimal values for all states all at once using successive approximations 19

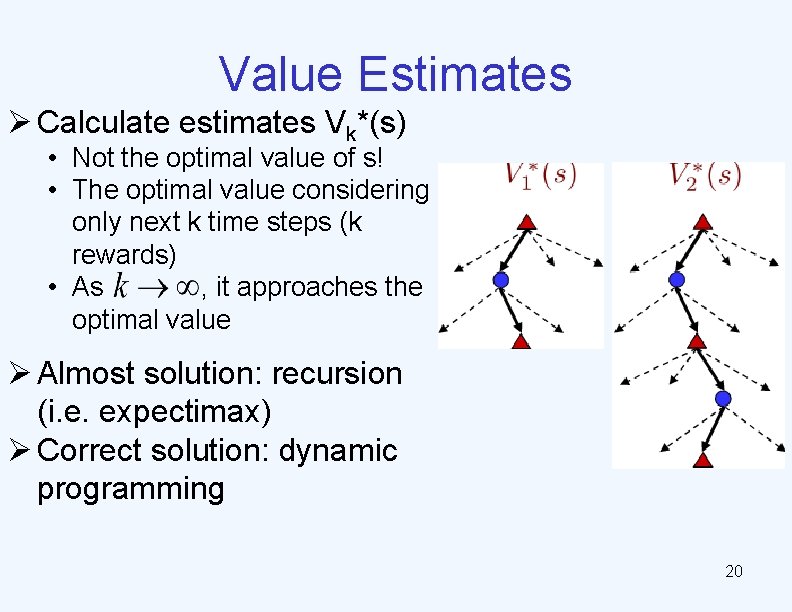
Value Estimates Ø Calculate estimates Vk*(s) • Not the optimal value of s! • The optimal value considering only next k time steps (k rewards) • As , it approaches the optimal value Ø Almost solution: recursion (i. e. expectimax) Ø Correct solution: dynamic programming 20

Computing the optimal policy ØValue iteration ØPolicy iteration 21

Value Iteration Ø Idea: • Start with V 1(s) = 0 • Given Vi, calculate the values for all states for depth i+1: • This is called a value update or Bellman update • Repeat until converge • Use Vi as evaluation function when computing Vi+1 Ø Theorem: will converge to unique optimal values • Basic idea: approximations get refined towards optimal values • Policy may converge long before values do 22

Example: γ=0. 9, living reward=0, noise=0. 2 Example: Bellman Updates max happens for a=right, other actions not shown 23

Example: Value Iteration Ø Information propagates outward from terminal states and eventually all states have correct value estimates 24

Convergence Ø Define the max-norm: Ø Theorem: for any two approximations U and V • I. e. any distinct approximations must get closer to each other, so, in particular, any approximation must get closer to the true U and value iteration converges to a unique, stable, optimal solution Ø Theorem: • I. e. once the change in our approximation is small, it must also be close to correct 25

Practice: Computing Actions Ø Which action should we chose from state s: • Given optimal values V? • Given optimal q-values Q? 26

Utilities for a Fixed Policy Ø Another basic operation: compute the utility of a state s under a fixed (generally non-optimal) policy Ø Define the utility of a state s, under a fixed policy π: Vπ(s)=expected total discounted rewards (return) starting in s and following π Ø Recursive relation (one-step lookahead / Bellman equation): 27

Policy Evaluation Ø How do we calculate the V’s for a fixed policy? Ø Idea one: turn recursive equations into updates Ø Idea two: it’s just a linear system, solve with Matlab (or other tools) 28

Policy Iteration Ø Alternative approach: • Step 1: policy evaluation: calculate utilities for some fixed policy (not optimal utilities!) • Step 2: policy improvement: update policy using one-step look-ahead with resulting converged (but not optimal!) utilities as future values • Repeat steps until policy converges Ø This is policy iteration • It’s still optimal! • Can converge faster under some conditions 29

Policy Iteration Ø Policy evaluation: with fixed current policy π, find values with simplified Bellman updates: Ø Policy improvement: with fixed utilities, find the best action according to one-step look-ahead 30

Comparison Ø Both compute same thing (optimal values for all states) Ø In value iteration: • Every iteration updates both utilities (explicitly, based on current utilities) and policy (implicitly, based on current utilities) • Tracking the policy isn’t necessary; we take the max Ø In policy iteration: • Compute utilities with fixed policy • After utilities are computed, a new policy is chosen Ø Both are dynamic programs for solving MDPs 31

Preview: Reinforcement Learning Ø Reinforcement learning: • Still have an MDP: • • A set of states A set of actions (per state) A A model T(s, a, s’) A reward function R(s, a, s’) • Still looking for a policy π(s) • New twist: don’t know T or R • I. e. don’t know which states are good or what the actions do • Must actually try actions and states out to learn 32