0 Wisdom of The Crowd Lirong Xia Example

0

Wisdom of The Crowd Lirong Xia

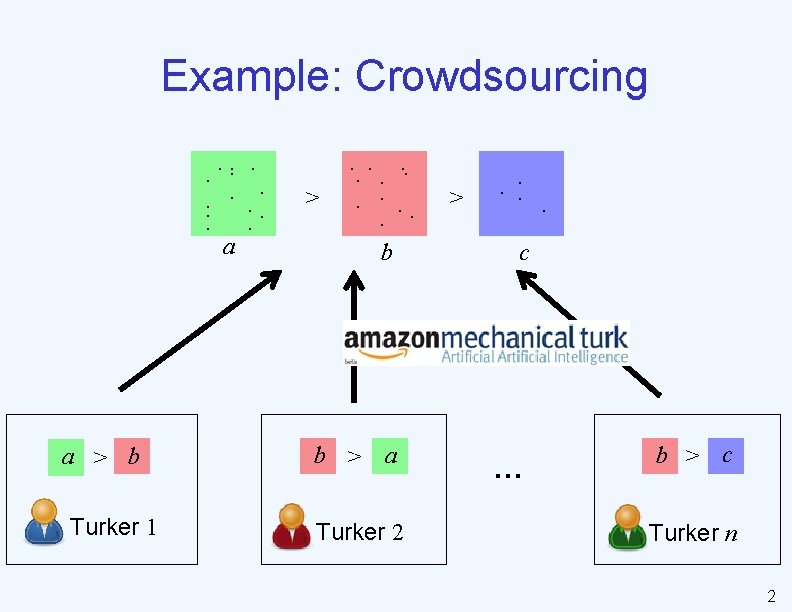
Example: Crowdsourcing. . . . a a > b Turker 1 . . . > . . . b b > a Turker 2 > . . c … b > c Turker n 2

The Condorcet Jury theorem [Condorcet 1785] The Condorcet Jury theorem. Pr( | ) = Pr( | ) Ø Given • two alternatives {O, M}. • 0. 5<p<1, Ø Suppose = p>0. 5 • each agent’s preferences is generated i. i. d. , such that • w/p p, the same as the ground truth • w/p 1 -p, different from the ground truth Ø Then, as n→∞, the majority of agents’ preferences converges in probability to the ground truth 3

Importance of the Jury Theorem ØJustifies democracy and wisdom of the crowd • “lays, among other things, the foundations of the ideology of the democratic regime” [Paroush SCW-98] 4

Proof Ø Group competence • Pr(maj(Pn)=a|a) • Pn: n i. i. d. votes given ground truth a Ø Random variable Xj : takes 1 w/p p, 0 otherwise • encoding whether signal=ground truth Ø Σj=1 n. Xj /n converges to p in probability (Law of Large Numbers) 5

Limitations of CJT Ø Given more than two? • two alternatives {a, b}. • competence 0. 5<p<1, heterogeneous agents? Ø Suppose dependent agents? • agents’ signals are i. i. d. conditioned on the ground truth • w/p p, the same as the ground truth • w/p 1 -p, different from the ground truth • agents truthfully report their signals strategic agents? Ø The majority rule reveals ground truth as n→∞ other rules? 6

Extensions ØDependent agents ØHeterogeneous agents ØStrategic agents ØMore than two alternatives 7

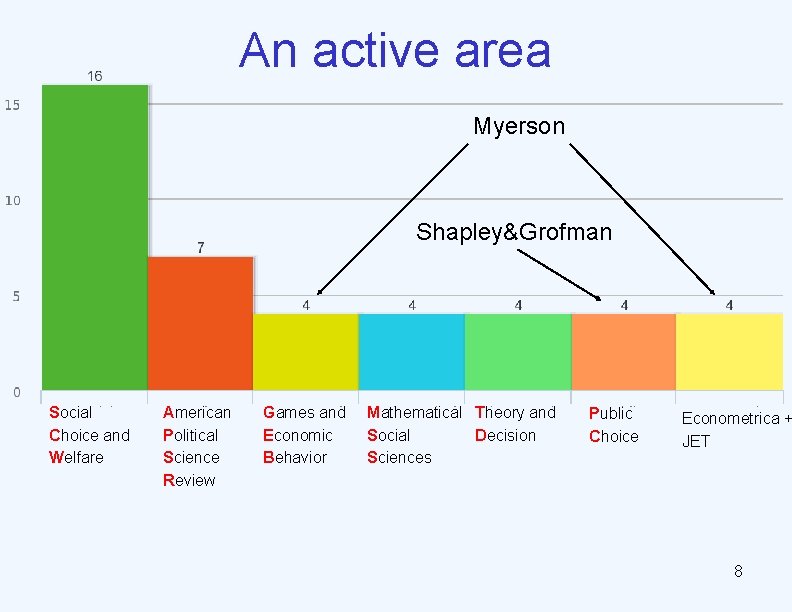
An active area Myerson Shapley&Grofman Social Choice and Welfare American Political Science Review Games and Economic Behavior Mathematical Theory and Social Decision Sciences Public Choice Econometrica + JET 8

Does CJT hold for strategic agents? The group competence 1. is higher than that of any single agent • Not always (same-vote equilibrium) 2. increases in the group size n • Not always (same-vote equilibrium) 3. goes to 1 as n→∞ • Yes for some models and informative equilibrium 9

Strategic voting Ø Common interest Bayesian voting game [Austen. Smith&Banks APSR-96] • two alternatives {a, b}, two signals {A, B}, a prior, Pr(signal|truth), • pa=Pr(signal=A|truth=a) • pb=Pr(signal=B|truth=b) • agents have the same utility function U(outcome, ground truth) =1 iff outcome = ground truth • sincere voting: vote for the alternative with the highest posterior probability • informative voting: vote for the signal • strategic voting: vote for the alternative with the highest expected utility 10

Timeline of the Bayesian game 1. Nature chooses a ground truth g 2. Every agent j receives a signal sj~Pr(sj|g) 3. Every agent computes the posterior distribution (belief) over the ground truth using Bayesian’s rule 4. Every agent chooses a vote to maximizes her expected utility according to her belief 5. The outcome is computed by the voting rule 11

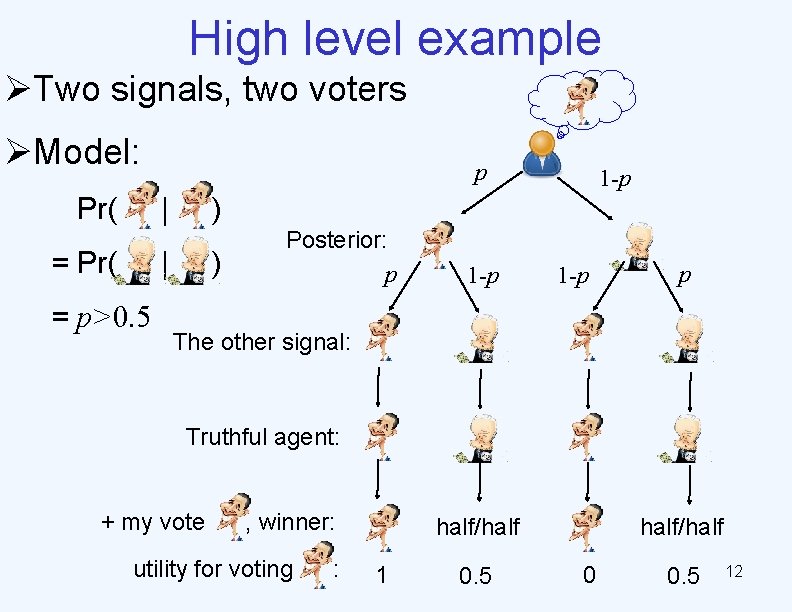
High level example ØTwo signals, two voters ØModel: Pr( p | = Pr( ) | = p>0. 5 1 -p ) Posterior: p 1 -p p The other signal: Truthful agent: + my vote , winner: utility for voting : half/half 1 0. 5 half/half 0 0. 5 12

Sincere voting vs. informative voting Ø Setting • • Two alternatives {a, b}, two signals {A, B} Three agents Pr(A|a) = pa=0. 6, Pr(B|b)=pb=0. 8 Prior: Pr(a)=0. 2, Pr(b)=0. 8 Ø An agent receives A • Informative voting: a • posterior probability: • Pr(a|A) ∝Pr(a)×Pr(A|a) = 0. 2× 0. 6 • Pr(b|A) ∝Pr(b)×Pr(A|b) = 0. 8×(1 -0. 8) • sincere voting: b 13

Strategic voting Ø Setting • Two alternatives {a, b}, two signals {A, B} • Three agents • Pr(A|a) = pa=0. 6, Pr(B|b)=pb=0. 8 • Prior: Pr(a)=0. 2, Pr(b)=0. 8 Ø An agent receives A, other two agents are informative • Conditioned on other two votes being {a, b} • Signal profile is (A, A, B) • Posterior probabilities • Pr(a|A, A, B) ∝Pr(a)×Pr(A|a)×Pr(B|a)=Pr(a)pa 2(1 -pa) =0. 2× 0. 62×(1 -0. 6)=0. 0288 • Pr(b|A, A, B) ∝Pr(b)×Pr(A|b)×Pr(B|b)=Pr(b) (1 -pb)2 pb =0. 8×(1 -0. 8)2× 0. 8=0. 0256 • Strategic voting: a 14

Eliciting Probabilities Ø Outcome space O = {o 1, …, om} • Example: {Sunny, Rainy} Ø An expert is asked for distribution q=(q 1, …, qm) over O • her true belief is p Ø Suppose the next day the weather is o, expert is awarded by a scoring rule s(q, o) • s: Lot(O) × O R • Example: linear scoring rule slin(q, ok) = qk Ø Expert’s expected utility • S(q, p) = ∑o∈Op(o)s(q, o) • When p = (0. 7, 0. 3), S(q, p) = 0. 7 q 1 + 0. 3 (1 -q 1), maximized at q 1=1 15

(Strictly) Proper Scoring Rules Ø A scoring rule s is strictly proper, if for all p, q∈Lot(O) such that p≠q S(p, p) > S(q, p) • reporting true belief is strictly optimal Ø Example (logarithm scoring rule). • slog(q, ok) = ln (qk) • For k =2, Slog(q, p) = p 1 ln(q 1) + (1 -p 1) ln(1 -q 1) • maximized at q 1 = p 1 Ø Example (quadratic scoring rule). • slog(q, ok) = 2 qk - ∑jqj 2 • For k =2, Slog(q, p) = 2 p 1 q 1 + 2(1 -p 1)(1 -q 1)-∑jqj 2 • maximized at q 1 = p 1 16

Characterization of Strictly Proper Scoring Rules Ø Theorem. For m=2, a scoring rule s(q, p) is strictly proper, if and only if G(p) = S(p, p) is strict convex. • Can be extended to m>2 17