LMITE DE UNA FUNCIN Definicin intuitiva de lmite

LÍMITE DE UNA FUNCIÓN

Definición intuitiva de límite. Consideremos la función El dominio es Df = R - {1} Evalúa la función en los números dados y explica el comportamiento. X y 0 0. 5 0. 8 0. 9999 0 0. 75 1. 44 1. 71 1. 9701 1. 9970 1. 9997 2 1. 5 1. 2 1. 1 1. 001 1. 0001 6 3. 75 2. 64 2. 31 2. 0301 2. 0030 2. 0003

En el primer cuadro, ¿a qué número se aproxima x? En el mismo cuadro, ¿a qué valor se aproxima y? Es decir, cuando x se aproxima lo más cercano posible a 1 por la izquierda, el valor de y tiende a 2. En el segundo cuadro, ¿a qué número se aproxima x? En el segundo cuadro, ¿a qué número se aproxima y? Es decir, cuando x se aproxima lo más cercano posible a 1 por la derecha, el valor de y tiende a 2. ¿Crees que si aproximamos todavía más los valores de x al valor dado, los valores de y se aproximen más al valor observado?

Concepto de límite SI f(x) SE ACERCA ARBITRARIAMENTE A UN NÚMERO L, CONFORME x SE APROXIMA A UN NÚMERO a TANTO POR LA IZQUIERDA COMO POR LA DERECHA, ENTONCES “EL LÍMITE DE f(x) CUANDO x TIENDE A a ES L”, LO CUAL SE DENOTA COMO:

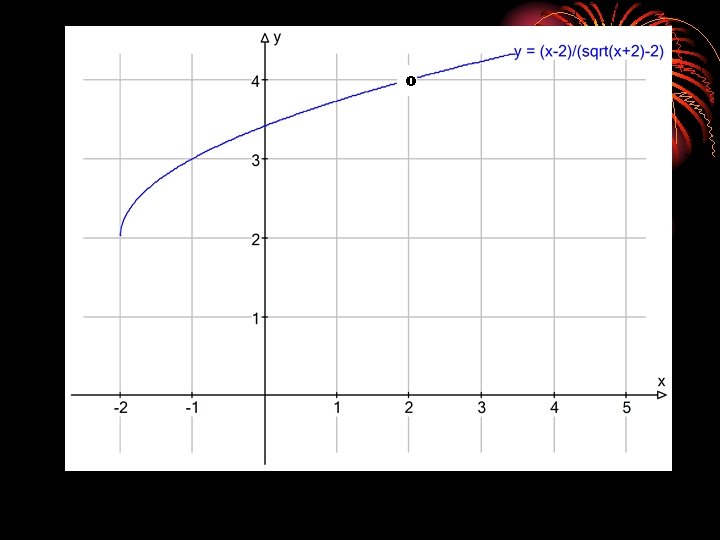
Ejemplo: Sea la función Hallar 2 X y 1. 8 1. 999 2. 001 2. 2 3. 9493 3. 9748 3. 9975 3. 9997 4. 0002 4. 0025 4. 0248 4. 0493 Por lo tanto

o

DEFINICIÓN FORMAL DEL LÍMITE DE UNA FUNCIÓN.

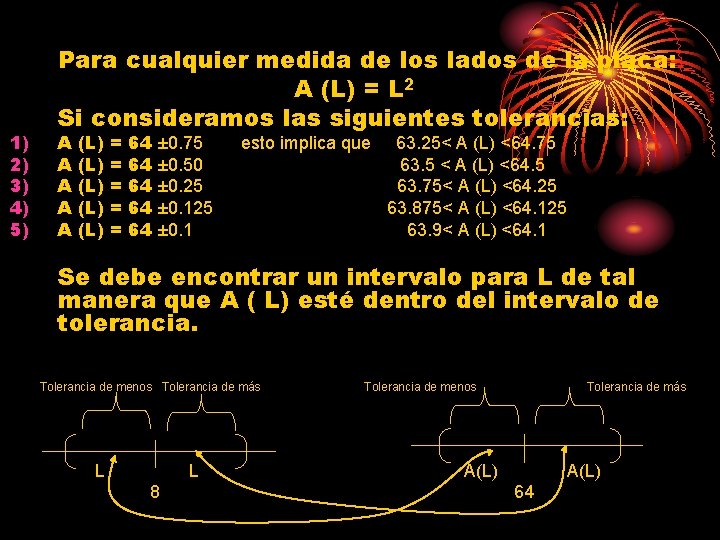
Se quiere fabricar placas de acero de 8 cm x 8 cm. 8 cm Es decir, de 64 cm 2 de superficie. En la realidad, resulta imposible fabricar placas con 64 cm 2 de superficie, siempre se elabora con cierta aproximación, o sea, que cumpla las especificaciones dentro de la tolerancia.

1) 2) 3) 4) 5) Para cualquier medida de los lados de la placa: A (L) = L 2 Si consideramos las siguientes tolerancias: A A A (L) (L) (L) = = = 64 64 64 ± 0. 75 ± 0. 50 ± 0. 25 ± 0. 1 esto implica que 63. 25< A (L) <64. 75 63. 5 < A (L) <64. 5 63. 75< A (L) <64. 25 63. 875< A (L) <64. 125 63. 9< A (L) <64. 1 Se debe encontrar un intervalo para L de tal manera que A ( L) esté dentro del intervalo de tolerancia. Tolerancia de menos Tolerancia de más L L 8 Tolerancia de menos Tolerancia de más A(L) 64

Es decir: Si 7. 96 < L < 8. 04 Si 7. 97 < L < 8. 03 Si 7. 99 < L < 8. 01 → → → 63. 25 < A (L) <64. 75 ¡cumple! 63. 5 < A (L) <64. 5 ¡cumple! 63. 75 < A (L) <64. 25 ¡cumple! Si se quiere más precisión de A (L), significa que L debe estar lo más cercano posible a 8. O sea, existe una pequeña diferencia de A (L) con 64, análogamente, existe también una pequeña diferencia de L con 8. Por la definición intuitiva de límite:

Si esas pequeñas diferencias que existen de L con 8 y de A (L) con 64 les llamamos δ(delta) y ε(épsilon) respectivamente, tendríamos: 8 – δ < L< 8 + δ ↔ 64 - ε < A (L) < 64 + ε ↔ Significa si y sólo si. También se puede escribir como: – δ < L - 8 < δ ↔ - ε < A (L) - 64 < ε Lo anterior quiere decir que si L se encuentra en el intervalo (8 - δ, 8+ δ), entonces A (L) se encuentra en el intervalo abierto (64 - ε, 64+ ε)

a x L f (x) a –δ a +δ L–ε L+ε Por propiedades del valor absoluto, las desigualdades: – δ < L - 8 < δ ↔ - ε < A (L) - 64 < ε Se pueden escribir como: Como el valor de L se aproxima a 8 sin llegar a ser 8, entonces L – 8 ≠ 0 y por lo tanto

De lo anterior: Ahora, generalizando para cualquier función f (x) cuando x → a, tenemos:

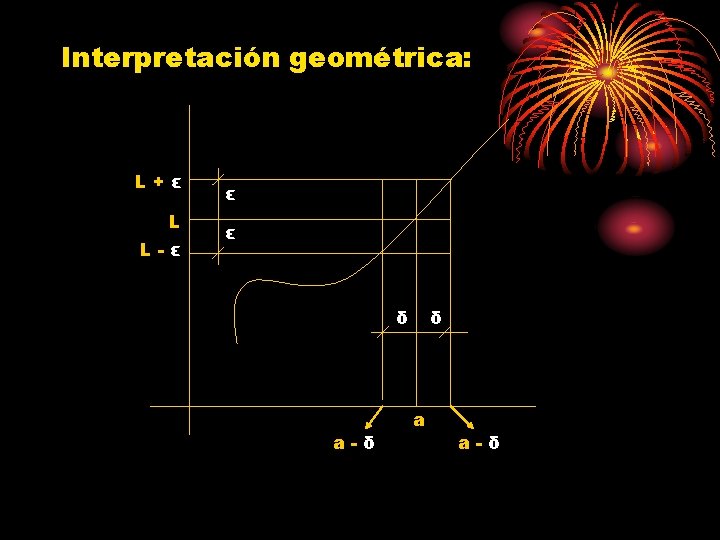
Definición formal de límite. Consideremos un intervalo abierto que contenga al número a. Sea f una función definida en todos los números del intervalo excepto posiblemente en a y sea L un número real. Entonces: Significa que para todo ε > 0 existe una δ > 0 tal que: Si 0 < | x – a | < δ, entonces | f (x) – L | < ε

Interpretación geométrica: L+ε L L-ε ε ε δ a-δ δ a a-δ

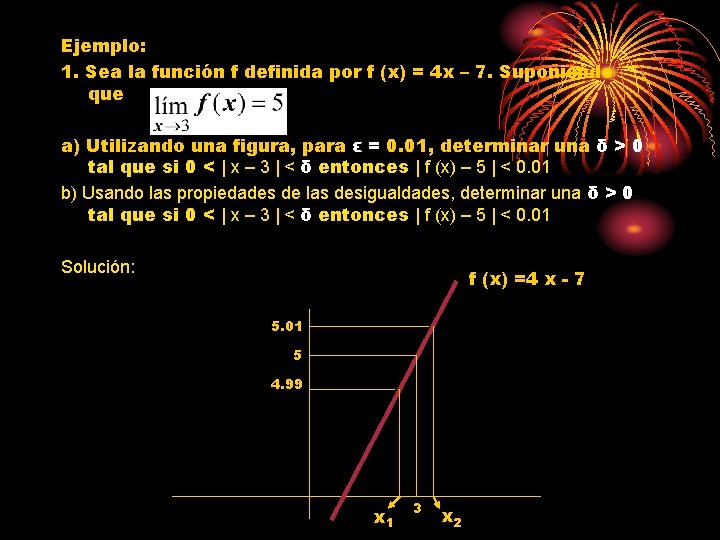
Ejemplo: 1. Sea la función f definida por f (x) = 4 x – 7. Suponiendo que a) Utilizando una figura, para ε = 0. 01, determinar una δ > 0 tal que si 0 < | x – 3 | < δ entonces | f (x) – 5 | < 0. 01 b) Usando las propiedades de las desigualdades, determinar una δ > 0 tal que si 0 < | x – 3 | < δ entonces | f (x) – 5 | < 0. 01 Solución: f (x) =4 x - 7 5. 01 5 4. 99 x 1 3 x 2

Solución a) 4 x 1 - 7 = 4. 99 4 x 2 – 7 = 5. 01 Como 3 – 2. 9975 = 0. 0025 Y 3. 0025 – 3 = 0. 0025 Se elige δ = 0. 0025, de tal forma que 0 < | x-3| < 0. 0025 entonces | f (x) – 5 | < 0. 01 Lo cual es verdadero.

Solución b) Para toda ε > 0 y δ > 0, se debe cumplir que: Donde a = 3, L = 5 y f (x) = 4 x – 7, ε = 0. 01 Entonces: 0 < | x - 3 | < δ si y sólo si | (4 x – 7) - 5 | < 0. 01 Tomando la segunda ecuación: | (4 x – 7) - 5 | < 0. 01 | 4 x – 7 - 5 | < 0. 01 | 4 x – 12 | < 0. 01 | 4 (x – 3 ) | < 0. 01 | 4 | | x – 3 | < 0. 01 4 | x – 3 | < 0. 01

Si tomamos entonces: 0 < |x - 3 | < δ si y solamente si es verdadero! Puesto que: 0 < | x - 3 | < 0. 0025 4 | x - 3 | < 4 ( 0. 0025 ) | 4 (x – 3) | < 0. 01 | 4 x - 12 | < 0. 01 | ( 4 x – 7) - 5 | < 0. 01 | f (x) - 5 | < 0. 01 QUEDA DEMOSTRADO! | (4 x – 7) - 3 | < ε