FUNCIONES ELEMENTALES DEFINICIN DE FUNCIN Una funcin es

FUNCIONES ELEMENTALES

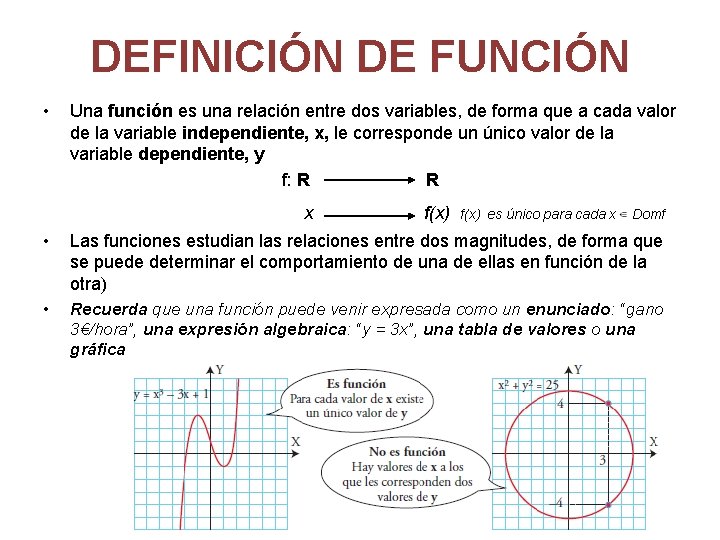
DEFINICIÓN DE FUNCIÓN • Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente, x, le corresponde un único valor de la variable dependiente, y f: R R x f(x) es único para cada x Domf • Las funciones estudian las relaciones entre dos magnitudes, de forma que se puede determinar el comportamiento de una de ellas en función de la otra) • Recuerda que una función puede venir expresada como un enunciado: “gano 3€/hora”, una expresión algebraica: “y = 3 x”, una tabla de valores o una gráfica.

TIPOS DE FUNCIONES 1. Funciones polinómicas (afín y cuadrática) 2. Funciones racionales 3. Funciones raíz 4. Funciones exponenciales 5. Funciones logarítmicas 6. Función valor absoluto 7. Funciones definidas a trozos 8. Funciones trigonométricas 9. Función parte entera 10. Función parte decimal

DOMINIO DE UNA FUNCIÓN DOMINIO, Domf (conjunto de valores que toma la variable independiente, x): • Polinómica: Estas expresiones están definidas para todos los números reales: Domf = R. • Racional: Un cociente no está definido cuando el denominador es 0 • Irracional: Las raíces de índice par solo están definidas para radicandos positivos. • Logaritmos: solo están definidos para números reales positivos. • Razones trigonométricas de seno y coseno: siempre están definidas. • La tangente: no está definida cuando el coseno es cero. Además debes tener en cuenta: • El contesto real del que se ha extraído la función (ejemplo: el área de un terreno) • Dónde ha sido definida la función (ejemplo: la recta y = 3 x – 8 definida en el intervalo x e (-1, 5] es un segmento rectilíneo) IMAGEN O RECORRIDO, Imf: El conjunto de valores que toma la función

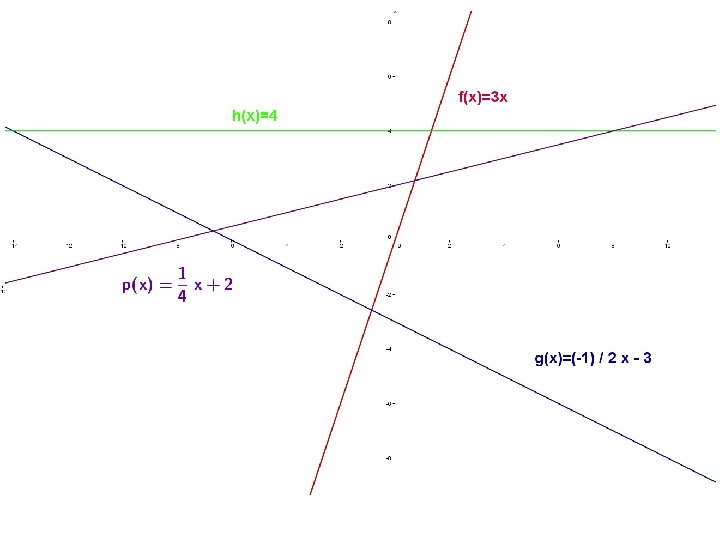
FUNCIONES POLINÓMICAS Función afín (Funciones lineales) Estudio • Su gráfica es una línea recta: • m = pendiente • n = ordenada en el origen ( si n = 0 la recta pasa por el origen de coordenadas y se llama función de proporcionalidad directa) • Dominio: R • Recorrido: R si m no es 0 / n si m = 0 • Monotonía: • Si m > 0 la recta es creciente • Si m < 0 la recta es decreciente • Si m = 0 la recta es constante

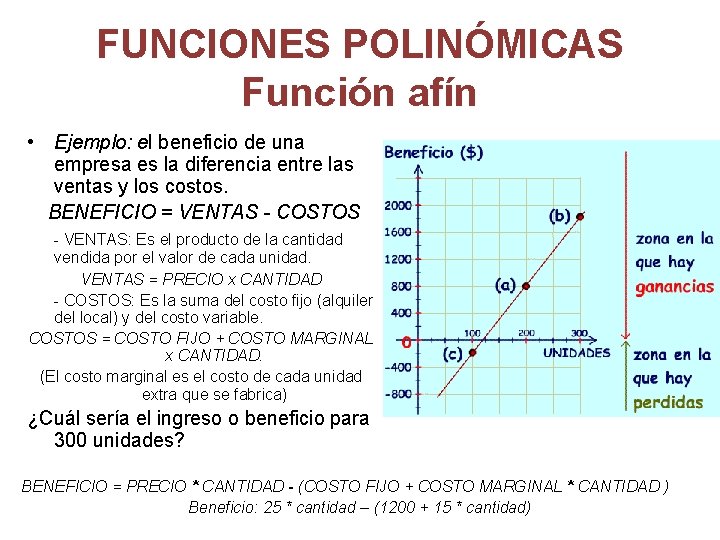
FUNCIONES POLINÓMICAS Función afín • Ejemplo: el beneficio de una empresa es la diferencia entre las ventas y los costos. BENEFICIO = VENTAS - COSTOS - VENTAS: Es el producto de la cantidad vendida por el valor de cada unidad. VENTAS = PRECIO x CANTIDAD - COSTOS: Es la suma del costo fijo (alquiler del local) y del costo variable. COSTOS = COSTO FIJO + COSTO MARGINAL x CANTIDAD. (El costo marginal es el costo de cada unidad extra que se fabrica) ¿Cuál sería el ingreso o beneficio para 300 unidades? BENEFICIO = PRECIO * CANTIDAD - (COSTO FIJO + COSTO MARGINAL * CANTIDAD ) Beneficio: 25 * cantidad – (1200 + 15 * cantidad)

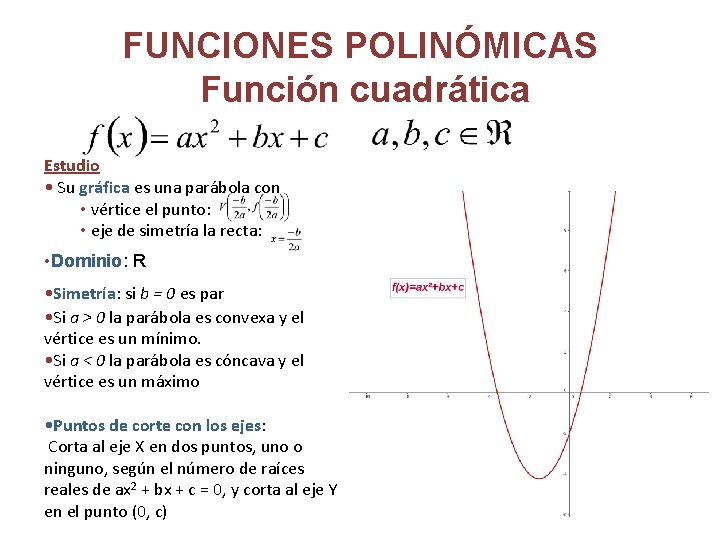
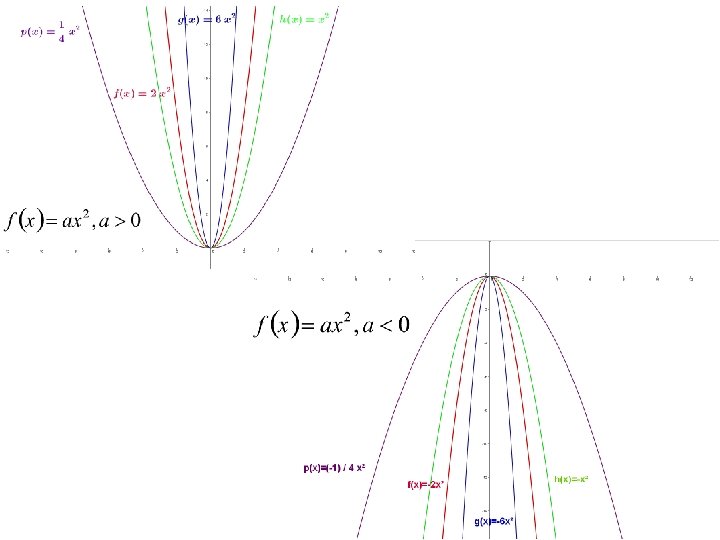
FUNCIONES POLINÓMICAS Función cuadrática Estudio • Su gráfica es una parábola con • vértice el punto: • eje de simetría la recta: • Dominio: R • Simetría: si b = 0 es par • Si a > 0 la parábola es convexa y el vértice es un mínimo. • Si a < 0 la parábola es cóncava y el vértice es un máximo • Puntos de corte con los ejes: Corta al eje X en dos puntos, uno o ninguno, según el número de raíces reales de ax 2 + bx + c = 0, y corta al eje Y en el punto (0, c)

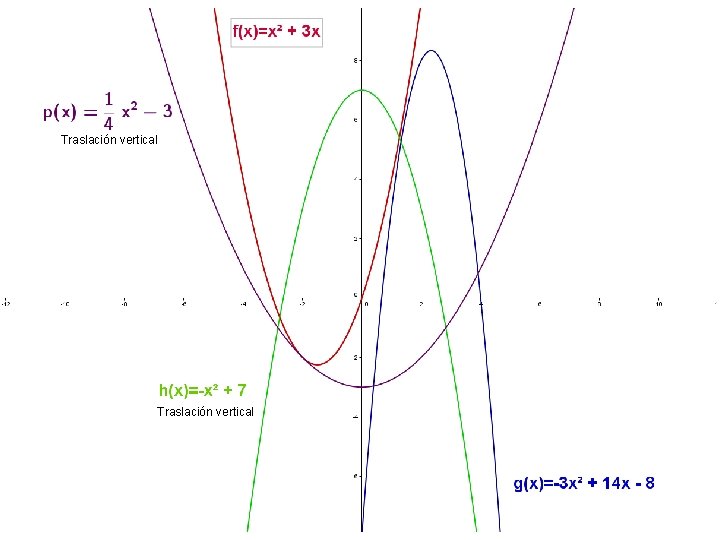
Traslación vertical

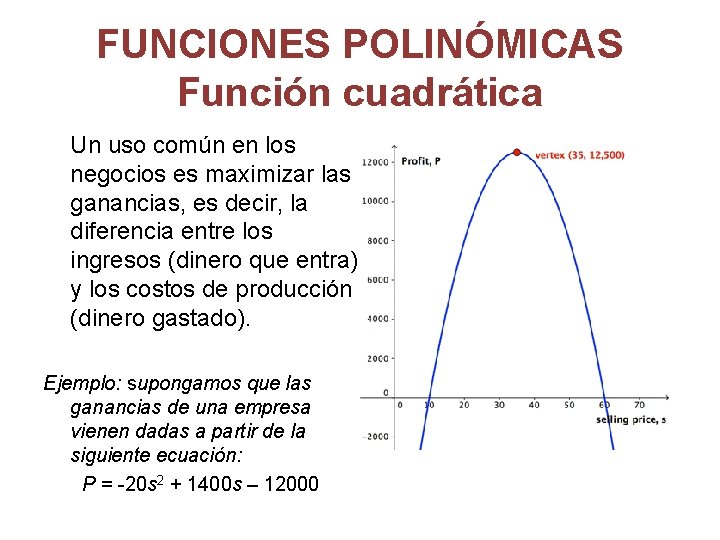
FUNCIONES POLINÓMICAS Función cuadrática Un uso común en los negocios es maximizar las ganancias, es decir, la diferencia entre los ingresos (dinero que entra) y los costos de producción (dinero gastado). Ejemplo: supongamos que las ganancias de una empresa vienen dadas a partir de la siguiente ecuación: P = -20 s 2 + 1400 s – 12000

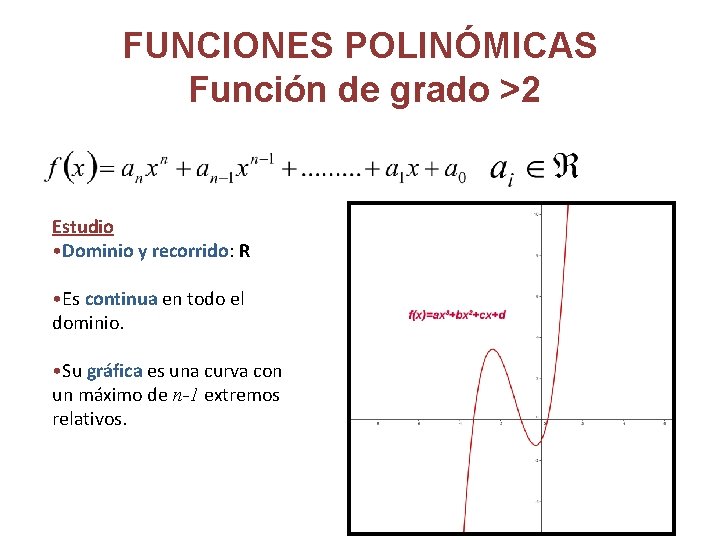
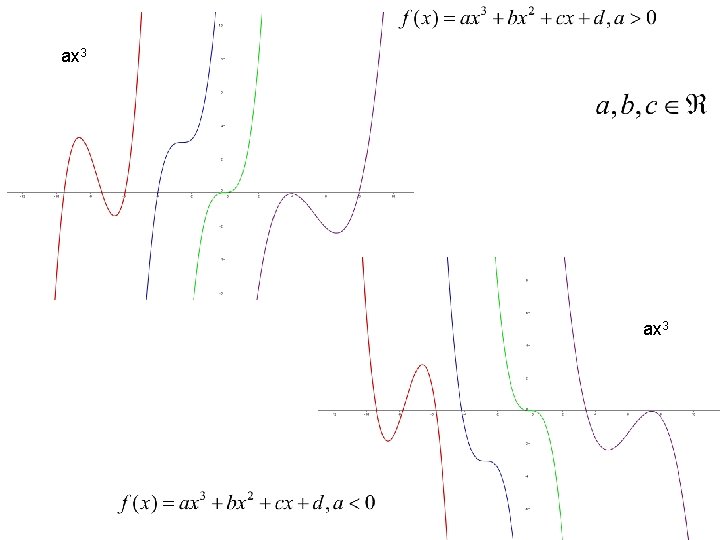
FUNCIONES POLINÓMICAS Función de grado >2 Estudio • Dominio y recorrido: R • Es continua en todo el dominio. • Su gráfica es una curva con un máximo de n-1 extremos relativos.

ax 3

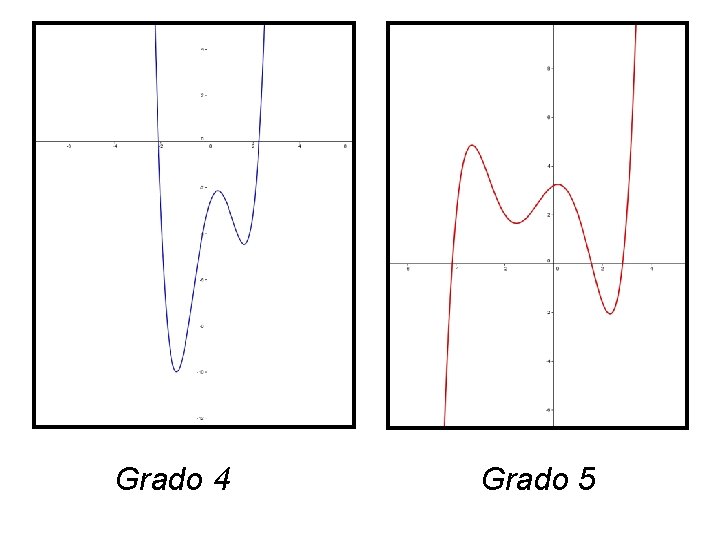
Grado 4 Grado 5

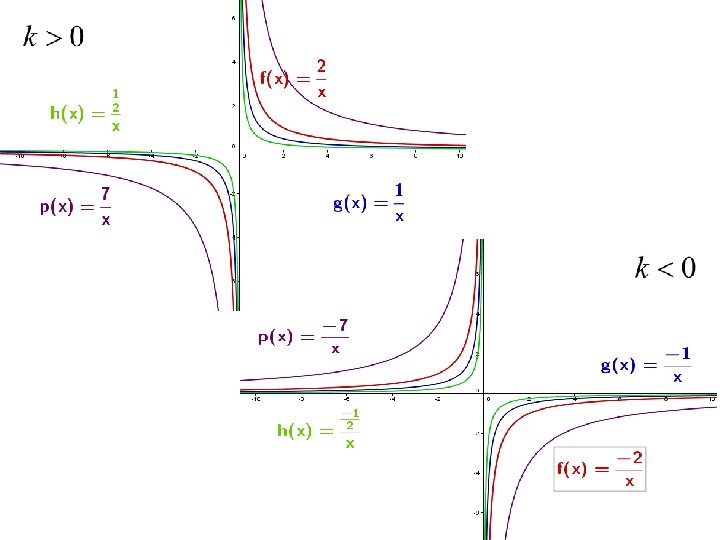
FUNCIONES RACIONALES Función de proporcionalidad inversa Estudio • Su gráfica es una hipérbola con asíntotas en los ejes de coordenadas. • Dominio: • Ramas: • Si k > 0 la hipérbola se sitúa en el primer y el tercer cuadrantes. Es decreciente en todo su dominio. • Si k < 0 la hipérbola se sitúa en el segundo y cuarto cuadrantes. Es creciente en todo su dominio. • Simetría: impar, respecto del origen de coordenadas

FUNCIONES RACIONALES

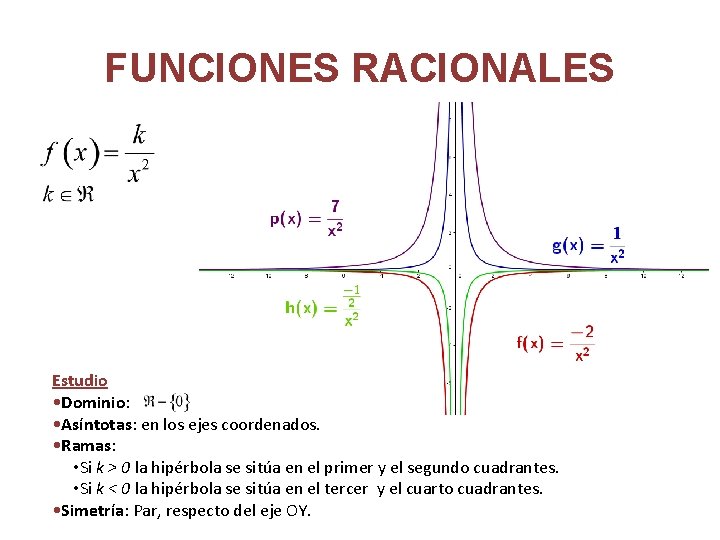
FUNCIONES RACIONALES Estudio • Dominio: • Asíntotas: en los ejes coordenados. • Ramas: • Si k > 0 la hipérbola se sitúa en el primer y el segundo cuadrantes. • Si k < 0 la hipérbola se sitúa en el tercer y el cuarto cuadrantes. • Simetría: Par, respecto del eje OY.

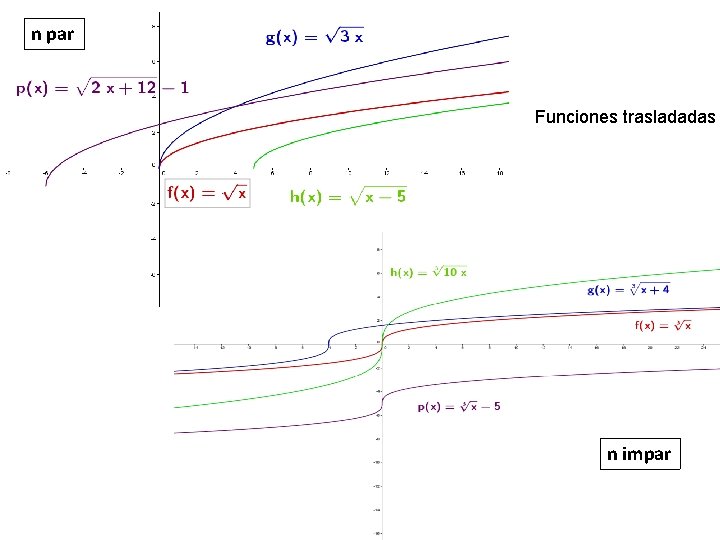
FUNCIONES RAÍZ (funciones irracionales) Estudio • Dominio: • Si n es par: el intervalo en el que n par • Si n es impar: • Monotonía: Creciente en todo su dominio (Para que sea función consideramos solo uno de los resultados, el positivo o el negativo) El periodo de un péndulo T (tiempo de una oscilación) en función de su longitud l: T =

n par Funciones trasladadas n impar

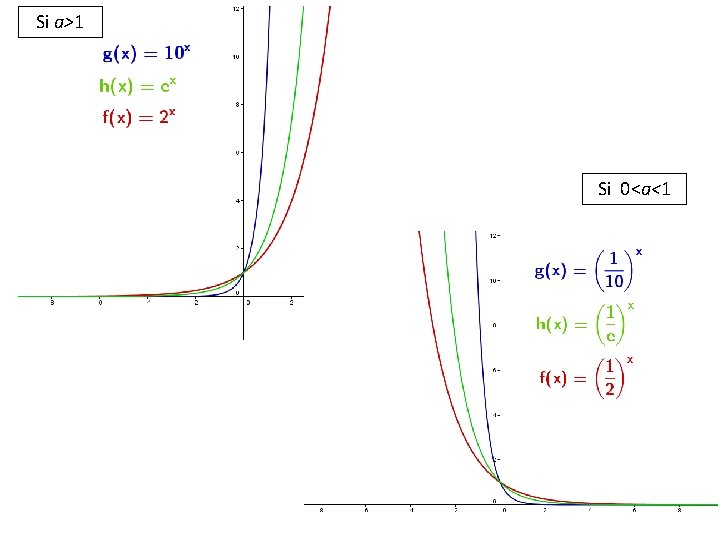
FUNCIONES EXPONENCIALES Estudio • Dominio: Recorrido: • Como a 0 = 1, la función pasa siempre por el punto (0, 1). • Como a 1 = a, la función pasa siempre por el punto (1, a). Si a>1 • Monotonía: son continuas y convexas • Si a>1: creciente. (Su crecimiento es muy rápido, superando incluso a cualquier función potencia) • Si 0<a<1: decreciente. • Asíntotas: asíntota horizontal en y = 0 (eje X) • Observa que las funciones f 1(x)=ax y f 2(x)=(1/a)x cumplen que f 1(-x)=f 2(x) y por tanto son simétricas respecto al eje Y Transformaciones elementales (de forma análoga a las anteriores)

Si a>1 Si 0<a<1

EJEMPLOS FUNCIONES EXPONENCIALES • Ejemplo 1: Algunos tipos de bacterias se reproducen por "mitosis", dividiéndose la célula en dos cada espacio de tiempo muy pequeños, en algunos casos cada 15 minutos. ¿Cuántas bacterias se producen en estos casos, a partir de una, en un día? 2 x siendo x el tiempo en minutos. En un día se producen 7, 9 1028 • Ejemplo 2: Interés compuesto (Crece si el rédito es positivo y decrece si el rédito es negativo)

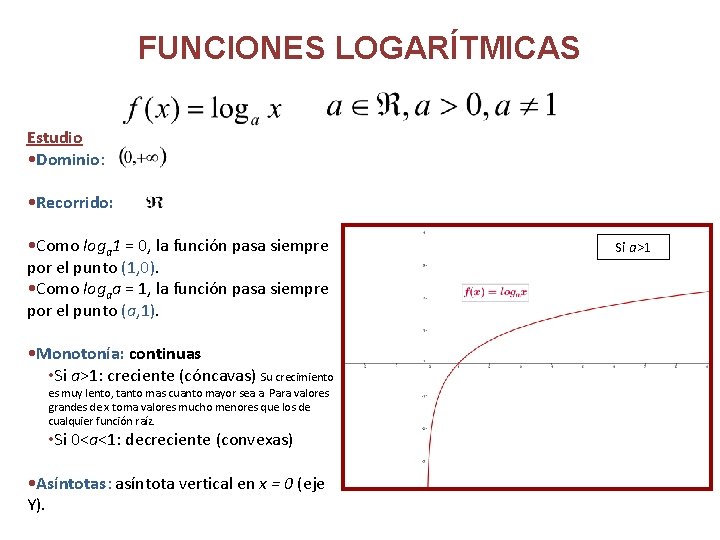
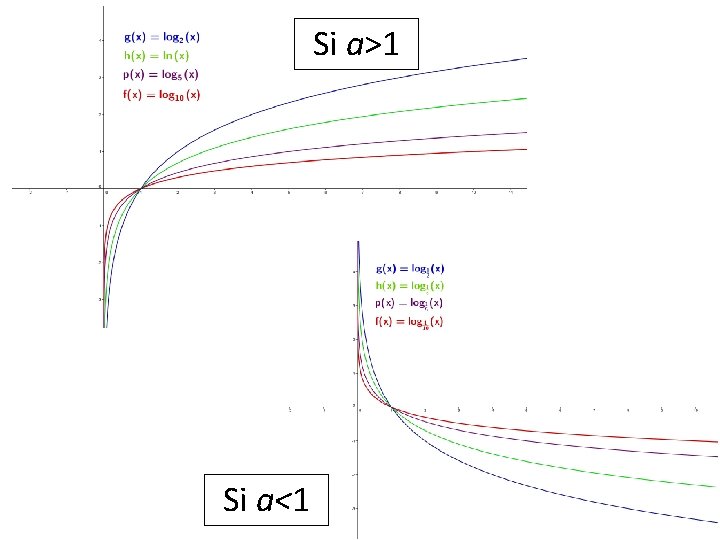
FUNCIONES LOGARÍTMICAS Estudio • Dominio: • Recorrido: • Como loga 1 = 0, la función pasa siempre por el punto (1, 0). • Como logaa = 1, la función pasa siempre por el punto (a, 1). • Monotonía: continuas • Si a>1: creciente (cóncavas) Su crecimiento es muy lento, tanto mas cuanto mayor sea a. Para valores grandes de x toma valores mucho menores que los de cualquier función raíz. • Si 0<a<1: decreciente (convexas) • Asíntotas: asíntota vertical en x = 0 (eje Y). Si a>1

Si a>1 Si a<1

EJEMPLOS FUNCIONES LOGARÍTMICAS • Ejemplo: en psicología tiene gran importancia el estudio de percepciones. El individuo percibe la luz, olores, etc. La percepción depende (es función) de los estímulos físicos. Por ejemplo, hablemos de la iluminación, I, y la percepción, S, que aprecia un individuo. La relación entre las dos variables viene dada por la ley psicológica o la ley de Weber-Fechner: siendo C una constante. Para valores pequeños de I el individuo aprecia pequeños cambios. Pero cuanto mayor sea I mayores tiene que ser los cambios para que se aprecien.

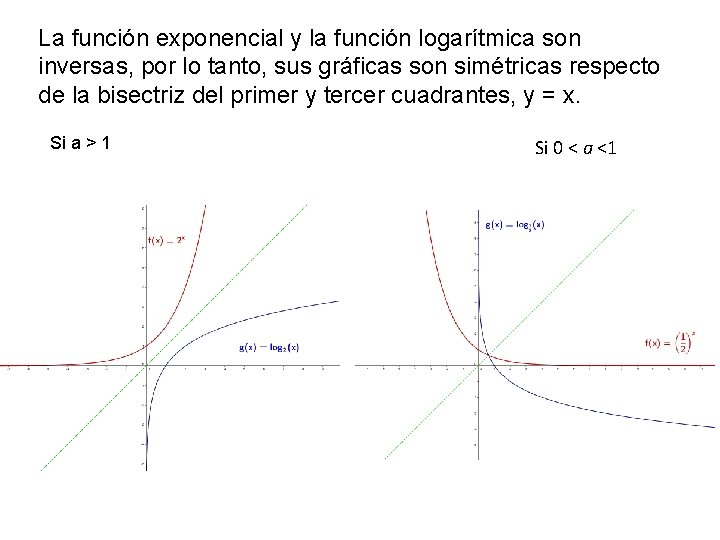
La función exponencial y la función logarítmica son inversas, por lo tanto, sus gráficas son simétricas respecto de la bisectriz del primer y tercer cuadrantes, y = x. Si a > 1 Si 0 < a <1

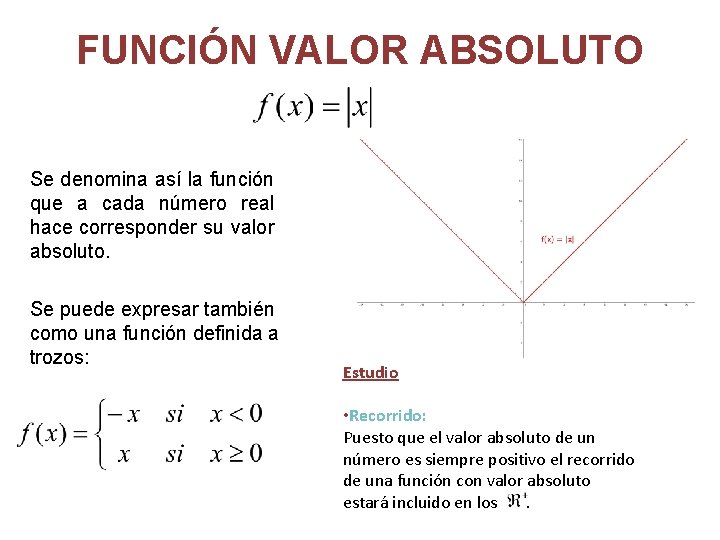
FUNCIÓN VALOR ABSOLUTO Se denomina así la función que a cada número real hace corresponder su valor absoluto. Se puede expresar también como una función definida a trozos: Estudio • Recorrido: Puesto que el valor absoluto de un número es siempre positivo el recorrido de una función con valor absoluto estará incluido en los.

FUNCIÓN VALOR ABSOLUTO De un polinomio A trozos: Para establecer los intervalos en los que P(x) tiene signo negativo hay que resolver la ecuación P(x)=0 y estudiar el signo de P en cada uno de los intervalos en los queda dividida la recta real. Para dibujar su gráfica, se dibuja normalmente y después se hace la simetría respecto del eje horizontal en aquellos tramos en los que la función sea negativa.

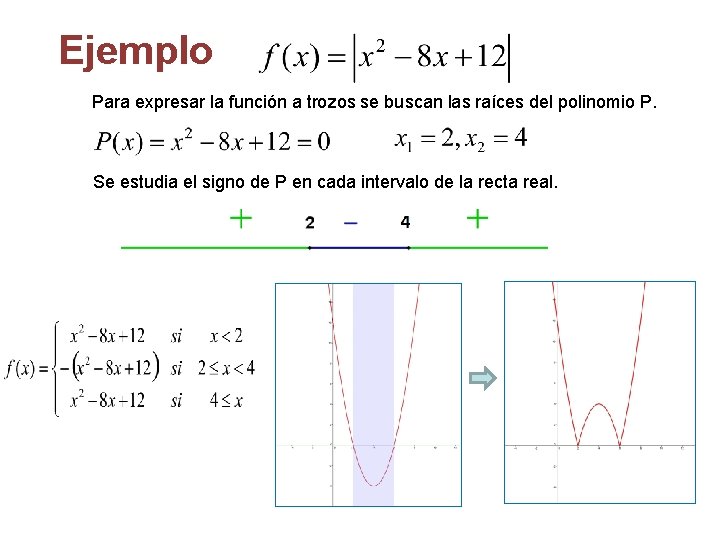
Ejemplo Para expresar la función a trozos se buscan las raíces del polinomio P. Se estudia el signo de P en cada intervalo de la recta real.

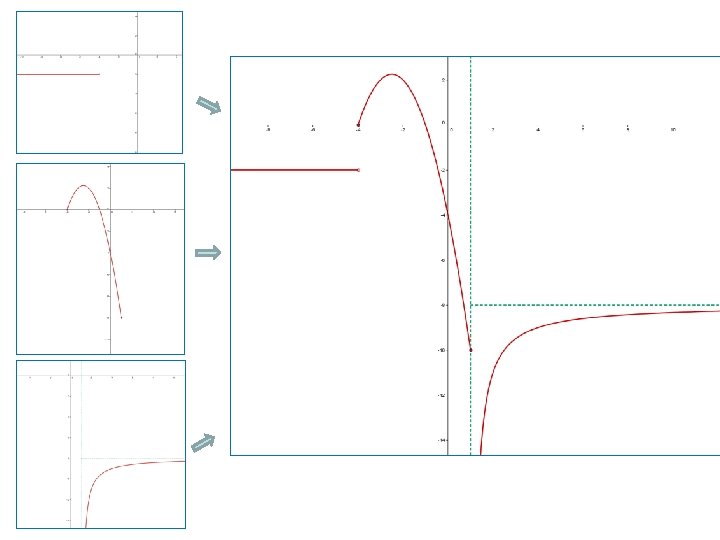
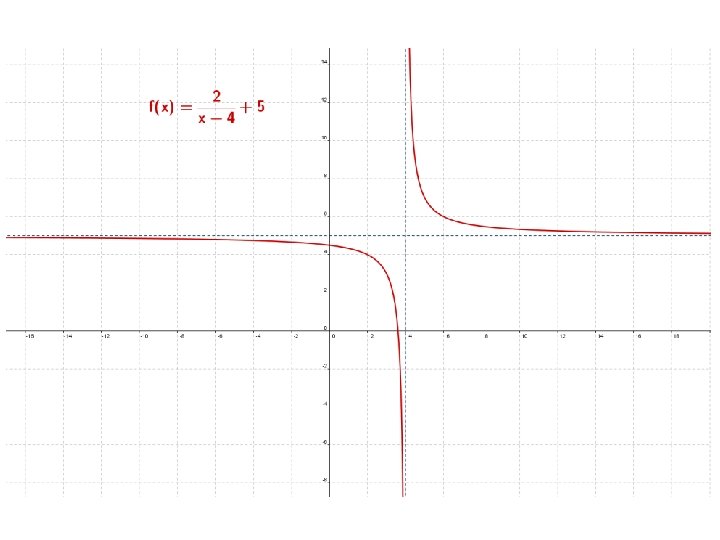
FUNCIONES DEFINIDAS A TROZOS Definición: “Una función definida a trozos es aquella cuyo dominio está dividido en intervalos disjuntos, de forma que en cada intervalo la función viene dada por expresiones matemáticas distintas”. Para dibujar las funciones a trozos tendremos que representar cada una de las partes de las que está compuesta teniendo en cuenta, además, que solo tienen validez en el intervalo en el que están definidas. Ejemplo:

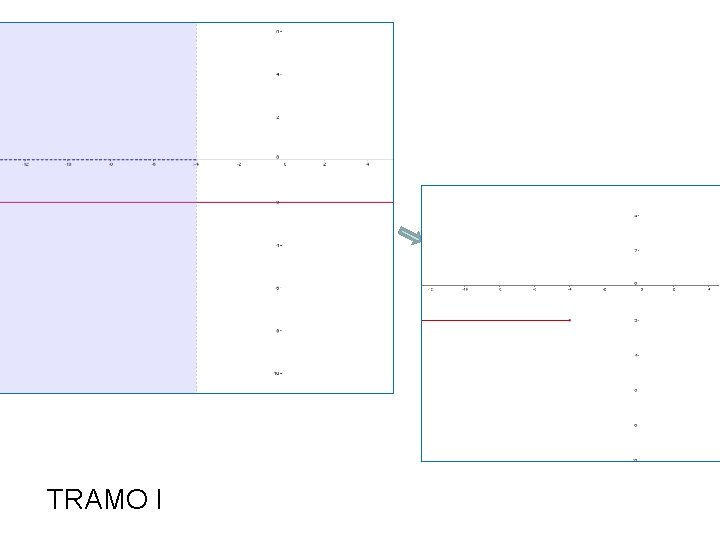
TRAMO I

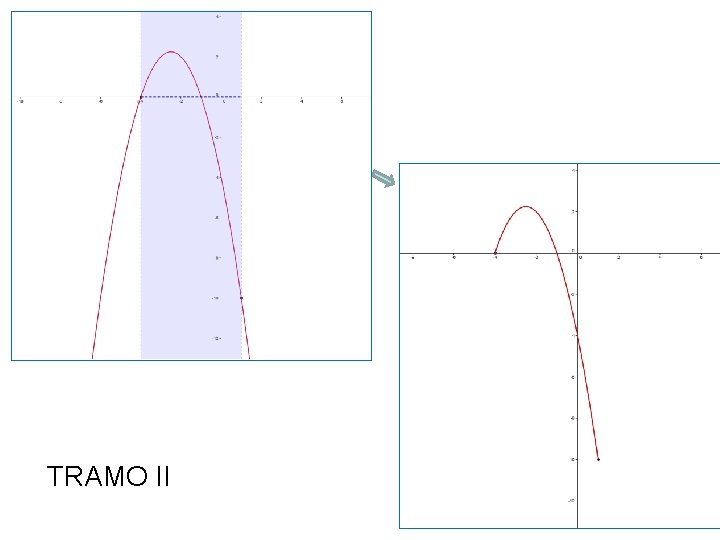
TRAMO II

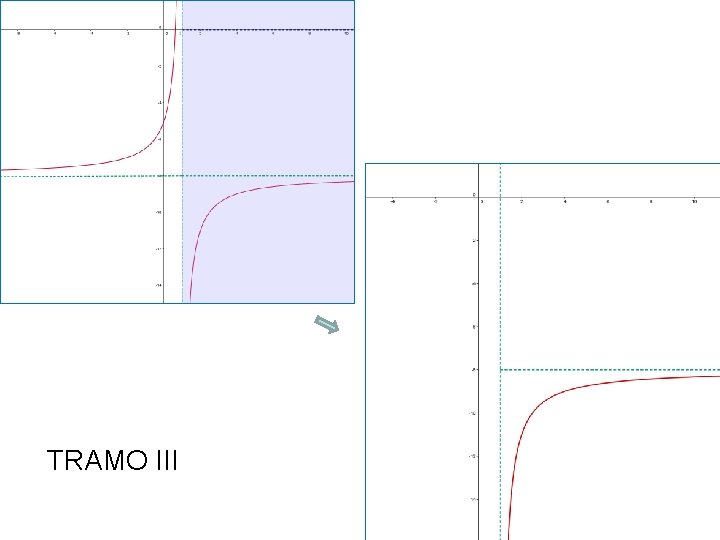
TRAMO III

TRANSFORMACIONES DE FUNCIONES •

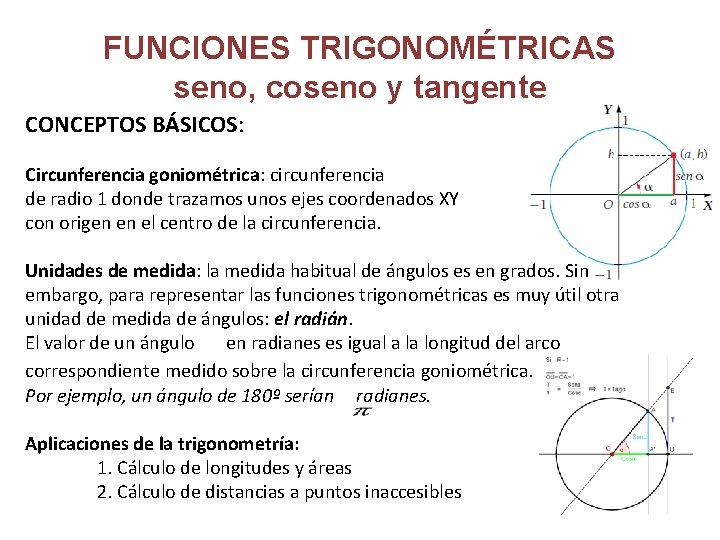
FUNCIONES TRIGONOMÉTRICAS seno, coseno y tangente CONCEPTOS BÁSICOS: Circunferencia goniométrica: circunferencia de radio 1 donde trazamos unos ejes coordenados XY con origen en el centro de la circunferencia. Unidades de medida: la medida habitual de ángulos es en grados. Sin embargo, para representar las funciones trigonométricas es muy útil otra unidad de medida de ángulos: el radián. El valor de un ángulo en radianes es igual a la longitud del arco correspondiente medido sobre la circunferencia goniométrica. Por ejemplo, un ángulo de 180º serían radianes. Aplicaciones de la trigonometría: 1. Cálculo de longitudes y áreas 2. Cálculo de distancias a puntos inaccesibles

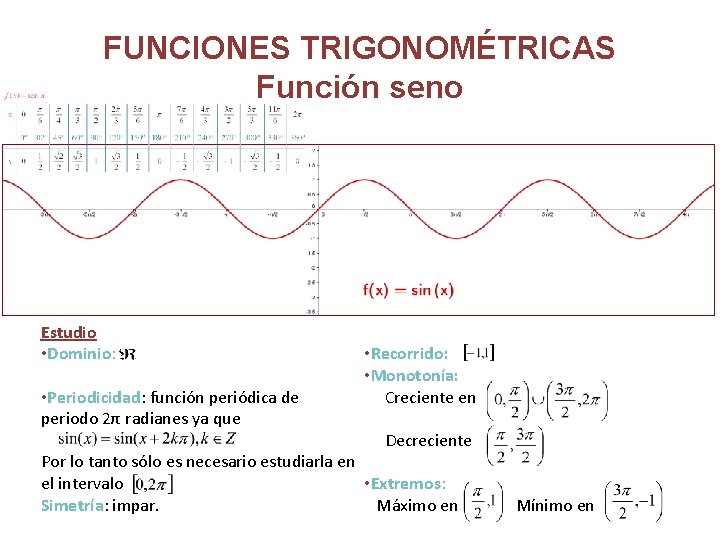
FUNCIONES TRIGONOMÉTRICAS Función seno Estudio • Dominio: • Periodicidad: función periódica de periodo 2π radianes ya que • Recorrido: • Monotonía: Creciente en Decreciente Por lo tanto sólo es necesario estudiarla en el intervalo • Extremos: Simetría: impar. Máximo en Mínimo en

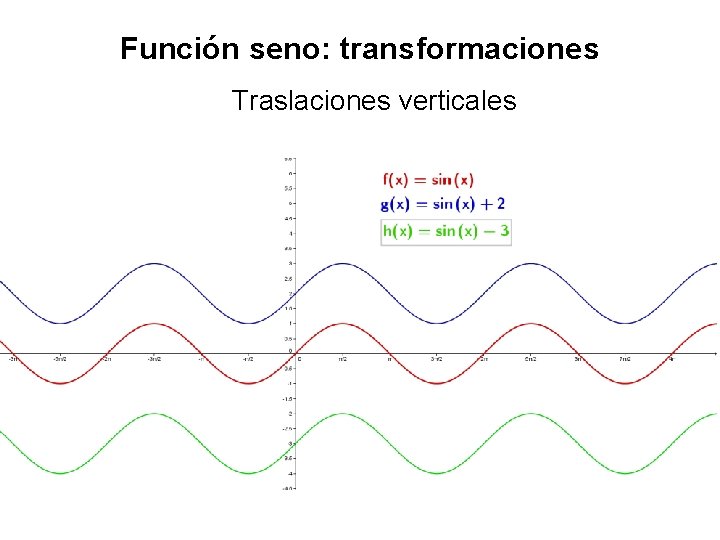
Función seno: transformaciones Traslaciones verticales

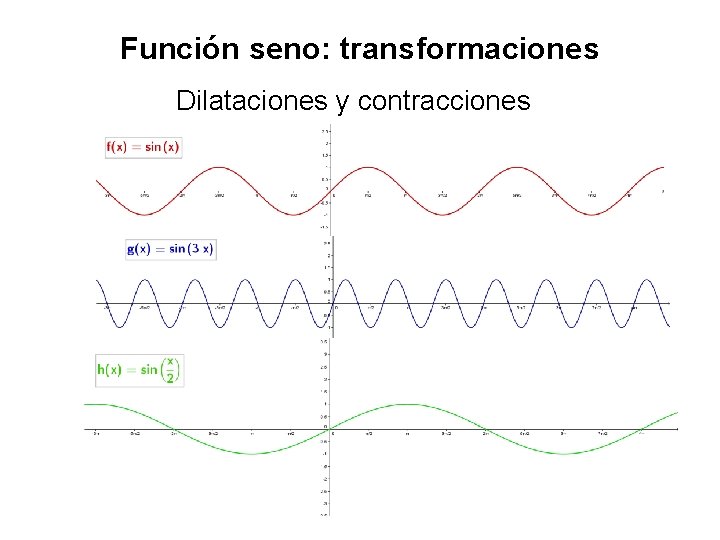
Función seno: transformaciones Dilataciones y contracciones

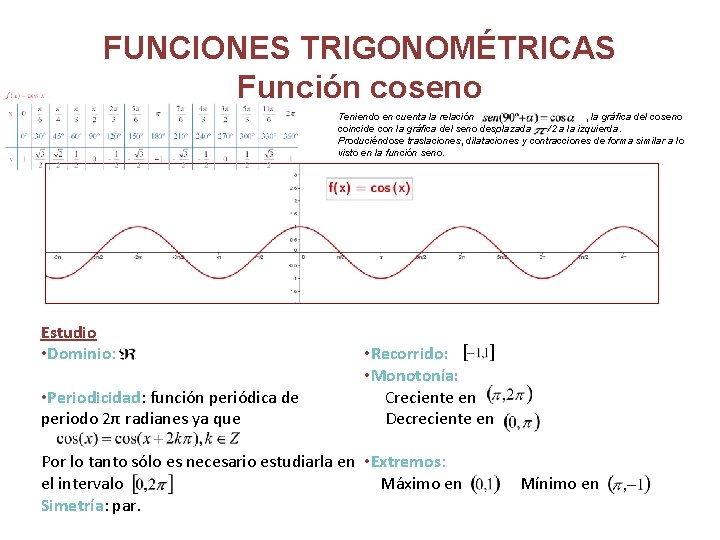
FUNCIONES TRIGONOMÉTRICAS Función coseno Teniendo en cuenta la relación , la gráfica del coseno coincide con la gráfica del seno desplazada /2 a la izquierda. Produciéndose traslaciones, dilataciones y contracciones de forma similar a lo visto en la función seno. Estudio • Dominio: • Periodicidad: función periódica de periodo 2π radianes ya que • Recorrido: • Monotonía: Creciente en Decreciente en Por lo tanto sólo es necesario estudiarla en • Extremos: el intervalo Máximo en Simetría: par. Mínimo en

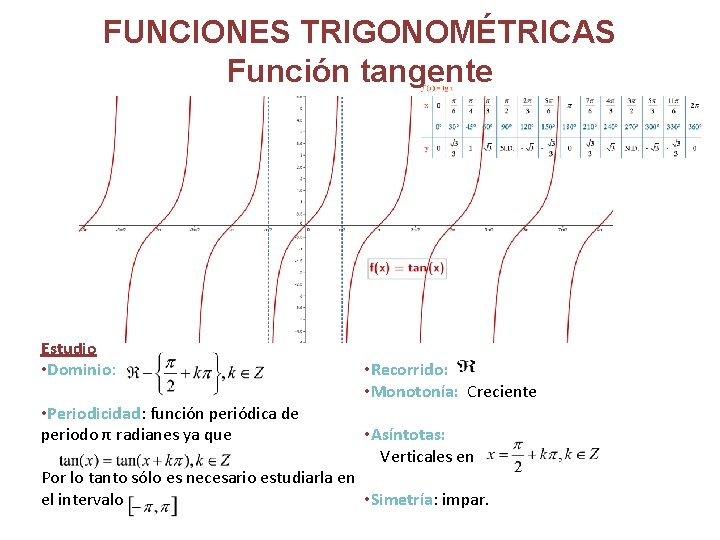
FUNCIONES TRIGONOMÉTRICAS Función tangente Estudio • Dominio: • Periodicidad: función periódica de periodo π radianes ya que • Recorrido: • Monotonía: Creciente • Asíntotas: Verticales en Por lo tanto sólo es necesario estudiarla en el intervalo • Simetría: impar.

FUNCIONES INVERSAS DE LAS TRIGONOMÉTRICAS

FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación f(x)=E[x], que a cada número real hace corresponder el mayor número entero que es menor o igual que él. Se puede expresar también como una función definida a trozos

FUNCIÓN PARTE DECIMAL La parte decimal o mantisa de un número x es Mant(x) = x – Ent(x) • A partir de esto, definimos la función decimal de x, Mant(x), que hace corresponder a cada número x su parte decimal.