Limits and Continuity Definition Evaluation of Limits Continuity







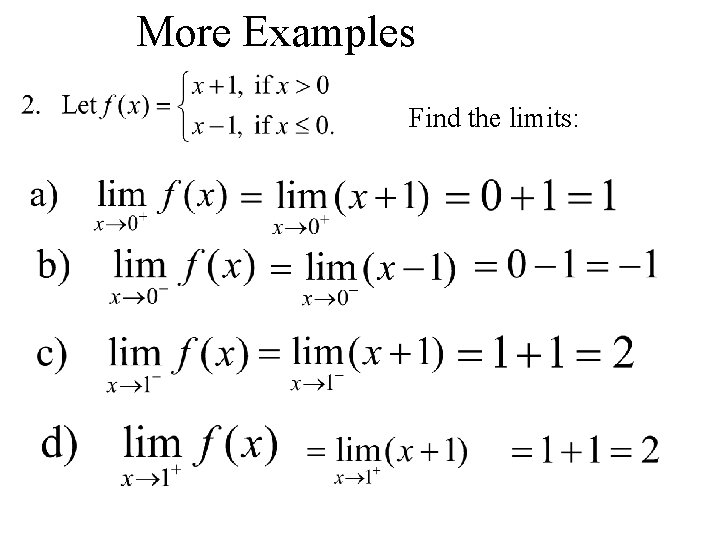



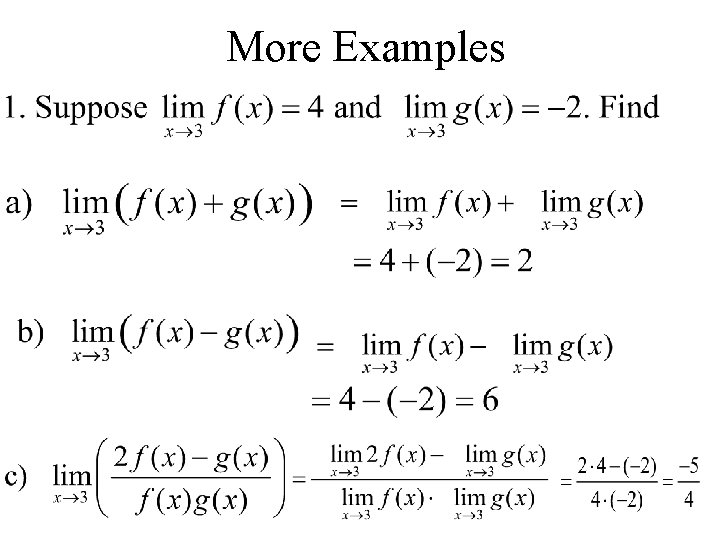

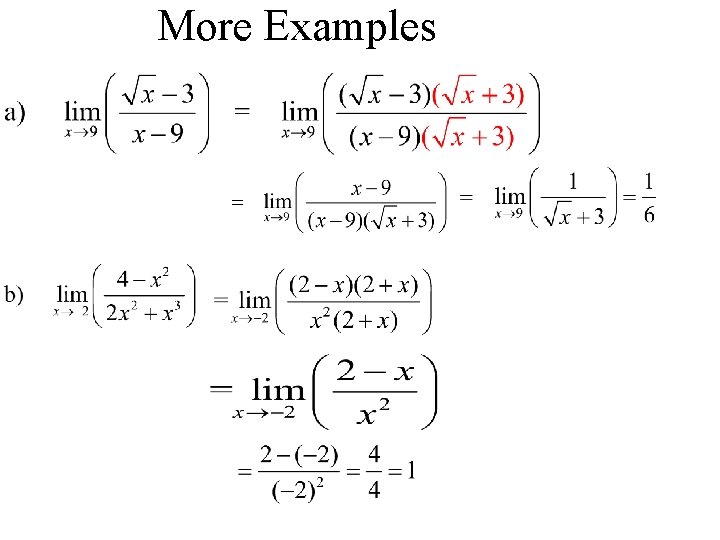












- Slides: 38

Limits and Continuity • Definition • Evaluation of Limits • Continuity • Limits Involving Infinity

Limit L a

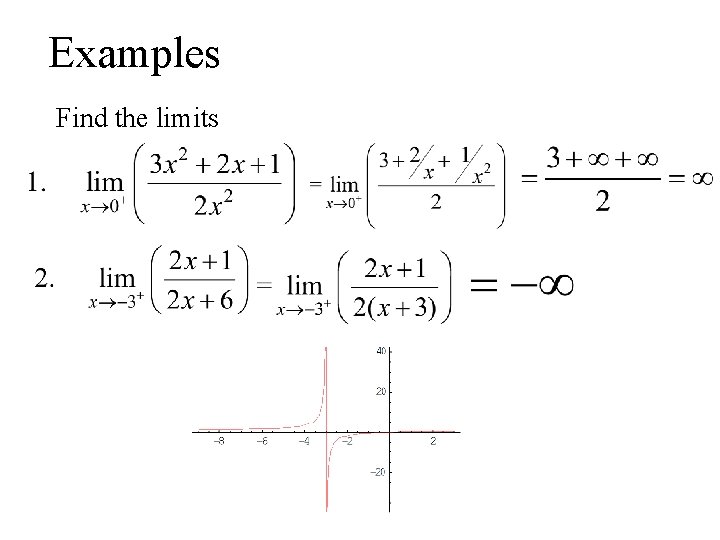
Limits, Graphs, and Calculators c) Use direct substitution Indeterminate form **If direct substitution results in an indeterminate form, then try factoring or rationalizing to simplify f(x) and then try direct substitution again,

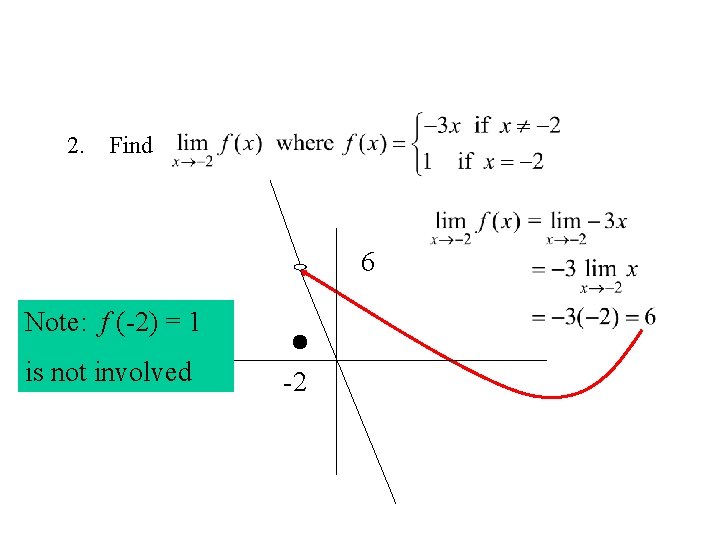
2. Find 6 Note: f (-2) = 1 is not involved -2

3) Use direct substitution to evaluate the limits Answer : 16 Answer : DNE Answer : 1/2

One-Sided Limits The right-hand limit of f (x), as x approaches a, equals L written: if we can make the value f (x) arbitrarily close to L by taking x to be sufficiently close to the right of a. L a

The left-hand limit of f (x), as x approaches a, equals M written: if we can make the value f (x) arbitrarily close to L by taking x to be sufficiently close to the left of a. M a

Examples of One-Sided Limit 1. Given Find
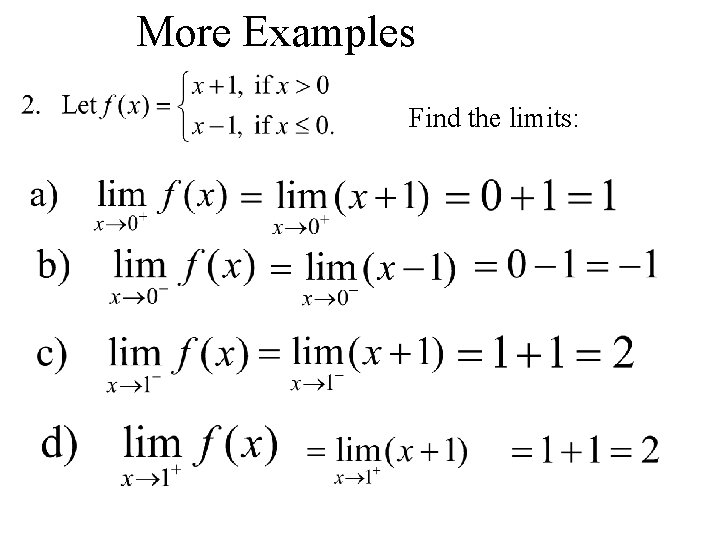
More Examples Find the limits:

A Theorem Memorize This theorem is used to show a limit does not exist. For the function But

Limit Theorems Page 99

Examples Using Limit Rule Ex.
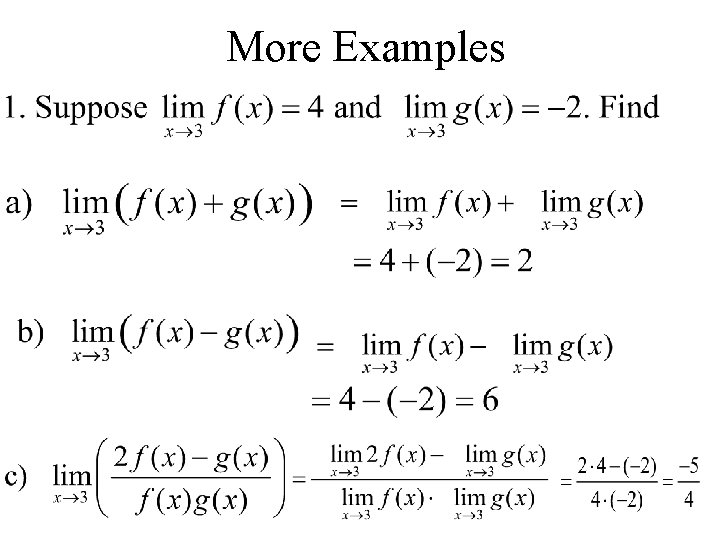
More Examples

Indeterminate Forms Indeterminate forms occur when substitution in the limit results in 0/0. In such cases either factor or rationalize the expressions. Ex. Notice form Factor and cancel common factors
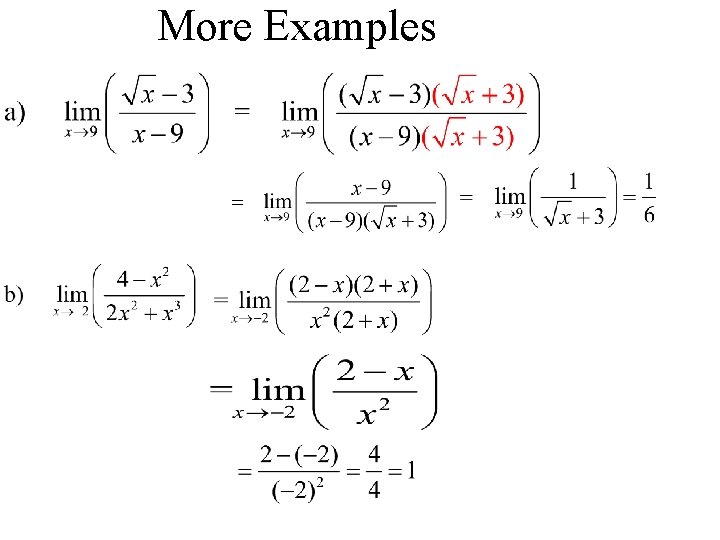
More Examples

The Squeezing Theorem See Graph

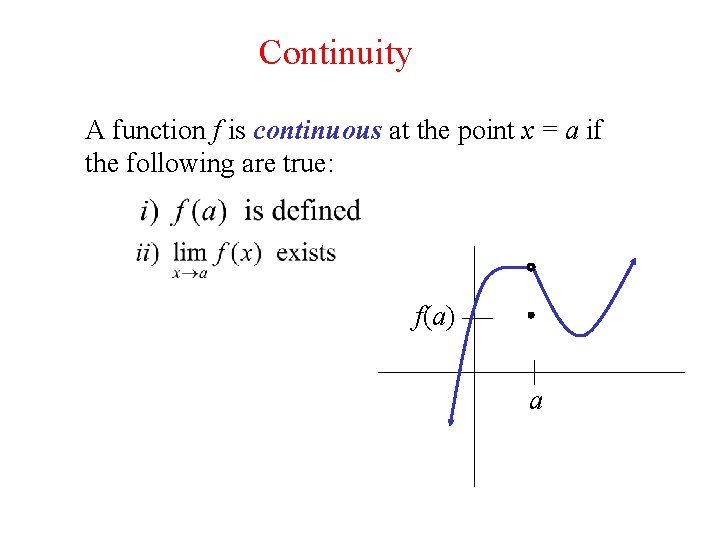
Continuity A function f is continuous at the point x = a if the following are true: f(a) a

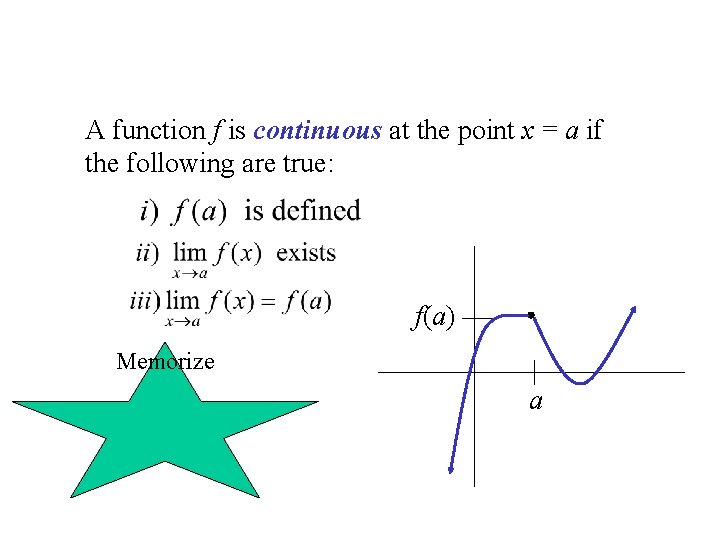
A function f is continuous at the point x = a if the following are true: f(a) Memorize a

Removable Discontinuities: (You can fill the hole. ) Essential Discontinuities: jump infinite oscillating

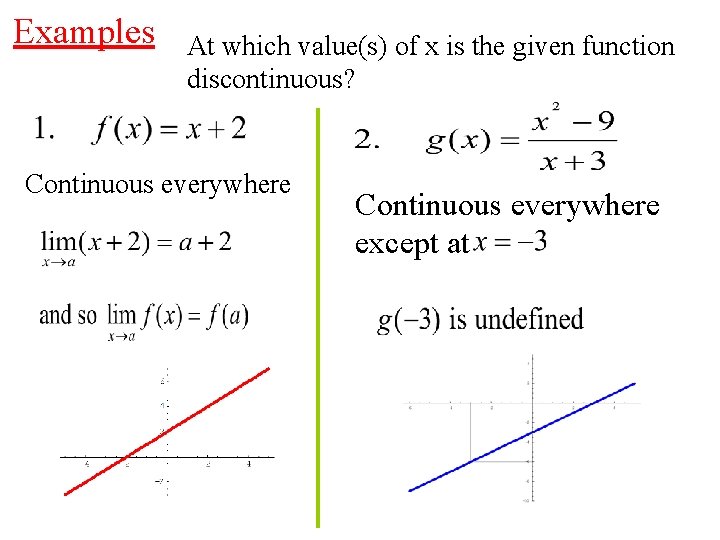
Examples At which value(s) of x is the given function discontinuous? Continuous everywhere except at

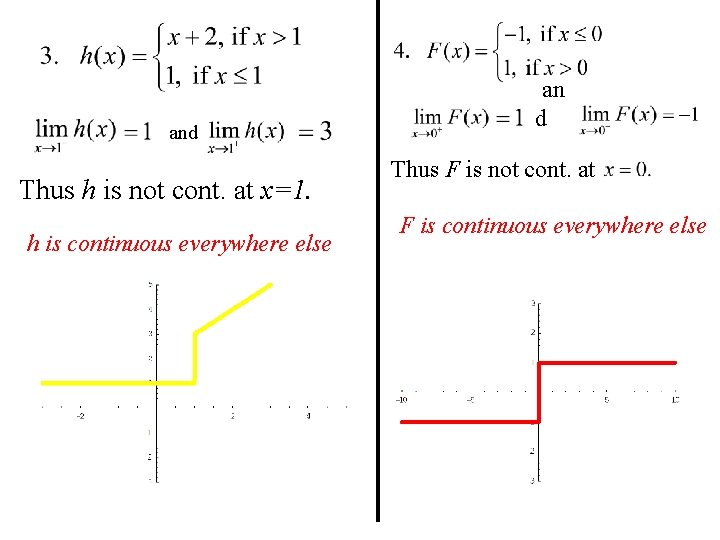
and Thus h is not cont. at x=1. h is continuous everywhere else an d Thus F is not cont. at F is continuous everywhere else

Continuous Functions If f and g are continuous at x = a, then A polynomial function y = P(x) is continuous at every point x. A rational function at every point x in its domain. is continuous

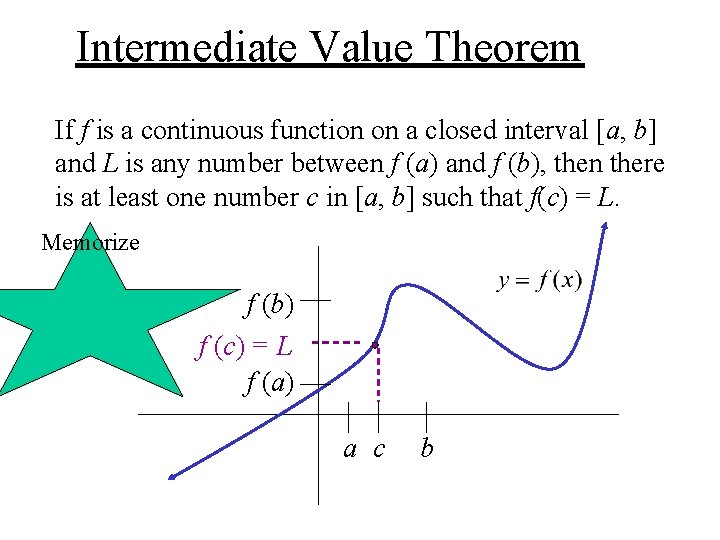
Intermediate Value Theorem If f is a continuous function on a closed interval [a, b] and L is any number between f (a) and f (b), then there is at least one number c in [a, b] such that f(c) = L. Memorize f (b) f (c) = L f (a) a c b

Example f (x) is continuous (polynomial) and since f (1) < 0 and f (2) > 0, by the Intermediate Value Theorem there exists a c on [1, 2] such that f (c) = 0.

Limits at Infinity For all n > 0, provided that Ex. is defined. Divide by

More Examples



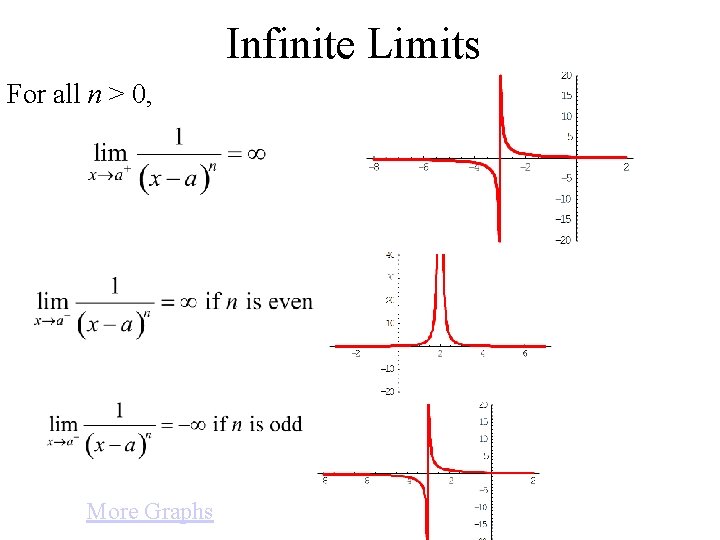
Infinite Limits For all n > 0, More Graphs

Examples Find the limits

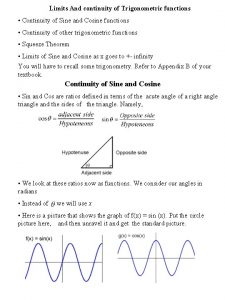
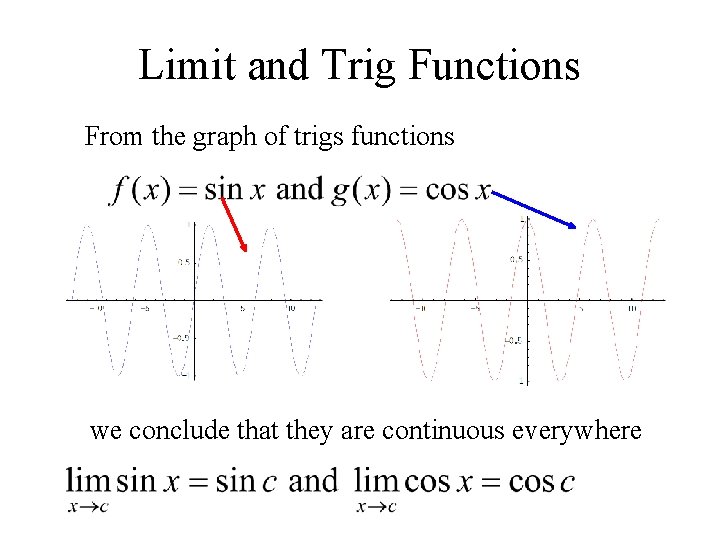
Limit and Trig Functions From the graph of trigs functions we conclude that they are continuous everywhere

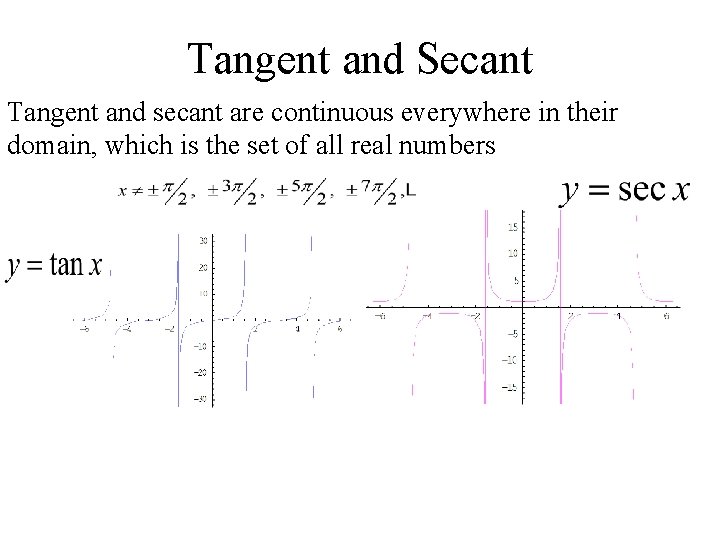
Tangent and Secant Tangent and secant are continuous everywhere in their domain, which is the set of all real numbers

Inverse tangent function • f(x)=tan x is not one-to-one • But the function f(x)=tan x , -π/2 < x < π/2 is one-to-one. The restricted tangent function has an inverse function which is denoted by tan-1 or arctan and is called inverse tangent function. • Example: tan-1(1) = π/4. • Limits involving tan-1:

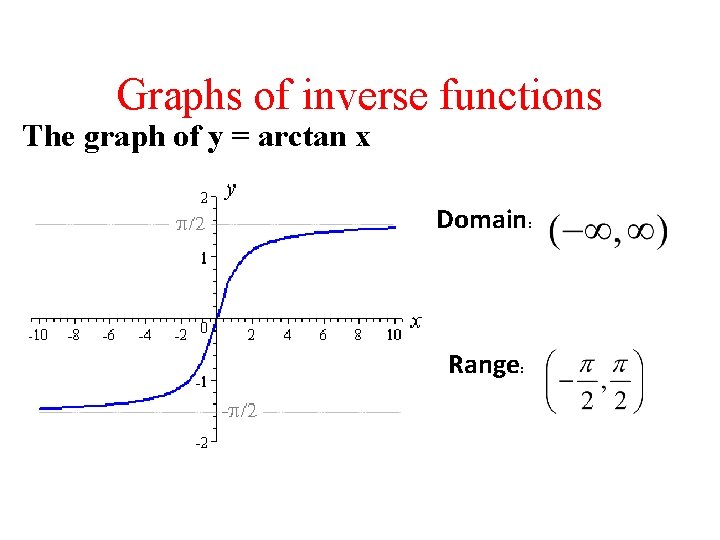
Graphs of inverse functions The graph of y = arctan x Domain: Range:

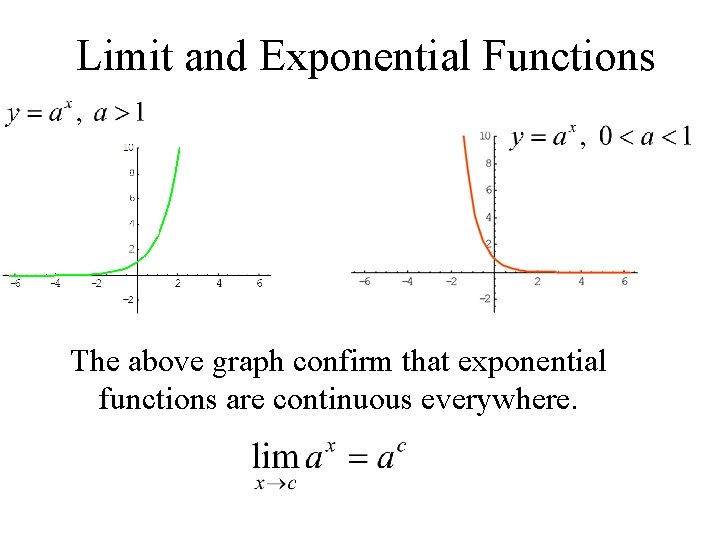
Limit and Exponential Functions The above graph confirm that exponential functions are continuous everywhere.

Asymptotes

Examples Find the asymptotes of the graphs of the functions

 Horizontal
Horizontal Limit and continuity solved problems
Limit and continuity solved problems Calculus chapter 2 limits and continuity
Calculus chapter 2 limits and continuity Thomas calculus limits and continuity
Thomas calculus limits and continuity Limits and continuity
Limits and continuity Limits and continuity
Limits and continuity Application of limits and continuity
Application of limits and continuity Real limits vs. apparent limits
Real limits vs. apparent limits Continuity assessment record and evaluation
Continuity assessment record and evaluation Absolute continuity implies uniform continuity
Absolute continuity implies uniform continuity Nature vs nurture definition psychology
Nature vs nurture definition psychology Beschouwende essay
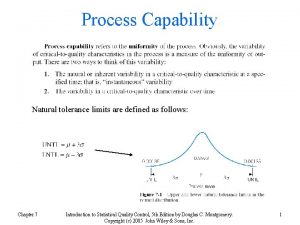
Beschouwende essay Natural tolerance limits in quality control
Natural tolerance limits in quality control Limits at infinity definition
Limits at infinity definition Limits at infinity definition
Limits at infinity definition How to find horizontal asymptotes
How to find horizontal asymptotes Classical continuity editing
Classical continuity editing Cell continuity
Cell continuity Continuity of operations plan definition
Continuity of operations plan definition Kutta–joukowski theorem
Kutta–joukowski theorem Continuity geography definition
Continuity geography definition Mitosis in a winter wonderland
Mitosis in a winter wonderland Limits fits and tolerances
Limits fits and tolerances Radiation dose limits for workers and public pdf
Radiation dose limits for workers and public pdf Difference between allowance and tolerance
Difference between allowance and tolerance Limits and their properties
Limits and their properties Limits and their properties
Limits and their properties Fundamental deviation table
Fundamental deviation table Ncert limits and derivatives pdf
Ncert limits and derivatives pdf Consistency limits and indices
Consistency limits and indices Limits and derivatives
Limits and derivatives Mathgotserved
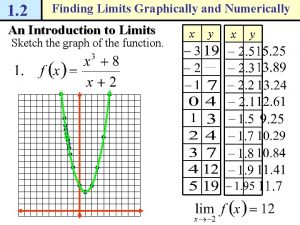
Mathgotserved Finding limits graphically and numerically
Finding limits graphically and numerically Find limit
Find limit Asymptote rules
Asymptote rules Estimating limits graphically
Estimating limits graphically Evaluating limits graphically
Evaluating limits graphically Limits graphically
Limits graphically Chapter 1 limits and their properties
Chapter 1 limits and their properties