Continuity and One Sided Limits 2 4 Continuity

Continuity and One Sided Limits 2. 4

Continuity Definition (with limits) • Continuity at a point: A function f(x) is continuous at point c if the following three condition are met: • 1) f(c) is defined • 2) • 3) exists

Continuity on an Open interval • A function is continuous on an open interval (a, b) if it is continuous at each point in the interval. A function continuous on the entire real line is said to be everywhere continuous.

Types of discontinuity • Removable discontinuity- a discontinuity at c is removable if the function f can be made continuous by redefining f(c). • Ex. Holes • Nonremovable discontinuity- if the function can not be made continuous by redefining a point (or finite set of points) • Ex. Asymptotes, Jump discontinuity

Continuity of a Function Examples • Is each function continuous or are there discontinuities? If so are the discontinuities removable or non-removable. • a) b) • c) d)

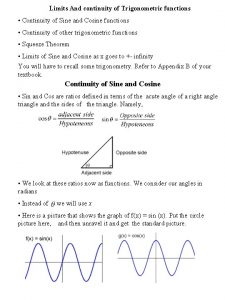
One-Sided Limits • Limit from the right (Right Hand Limit) means that x approaches c from values greater than c. • Limit from the left (Left Hand Limit) means that x approaches c from values less than c.

The Existence of a Limit • Let f be a function and let c and L be real number. The limits of f(x) as x approaches c is L if and only if And

Continuity on a Closed interval • A function is continuous on an closed interval [a, b] if it is continuous on the open interval (a, b) and • The function f is continuous from the right at a and continuous from the left at b

Properties of Continuity • If b is a real number and f and g are continuous at x = c, then the following function are also continuous at c. • • 1) Scalar multiple 2) Sum and difference 3) Product 4) Quotient if

Continuity of a Composite Function • If g is continuous at c and f is continuous at g(c), then the composite function f(g(x)) is continuous at c.

Intermediate Value Theorem • If f continuous on the closed interval [a, b] and k is any number between f(a) and f(b), then there is at least one number c in the interval [a, b] such that f(c)= k This is very useful because if we have two output values of different signs, it tells us that a zero (root) must exist between them.

Using the Intermediate Value theorem • Show that the polynomial has a zero in the interval [0, 1]. To actually find the zero we could use the “bisection method”. If we know that a zero falls in an interval [a , b]. We can split it into two intervals and Using the sign of (a + b)/2 we can determine which interval the zero falls in, and narrow in on this. We can repeat this process until we have located the zero.

Infinite Limits • Let’s examine two limits numerically (by plugging values into a table) from both the left and the right.

Approaching from the right x 0. 1 0. 001 0. 0001 Approaching from the left x -0. 1 -0. 001 -0. 0001

Approaching from the right x 0. 1 0. 001 0. 0001 Approaching from the left x -0. 1 -0. 001 -0. 0001

Infinite Limits Means that we can make f(x) arbitrarily large for all x values sufficiently close to x = c from both sides without actually letting x = c. Means that we can make f(x) arbitrarily “large” and negative for all x values sufficiently close to x = c from both sides without actually letting x = c.

Infinite limits still do not exist! • The equal sign in the statement does not mean the limit exists. It tells you the limit fails to exist by showing that f(x) is unbounded as x approaches c.

Vertical Asymptotes • If f(x) approaches infinity (or negative infinity) as x approaches c from the right or left, then the line x = c is a vertical asymptote of the graph of f.

Determine the vertical asymptotes of the graphs of each function

Properties of Infinite limits Let c and L be real numbers and let f and g be functions: 1) Sum or difference: 2) Product: 3) Quotient:

Use Infinite Limits and their Properties to Determine the following Limits

Hw • Continuity • Page 100 - 83 -91 odd 92, 93, 108 • Infinite limits • Page 108 1, 9, 11, 13, 23, 39, 43, 47, 48, 49, 51, 67