Lecture 2 MGMT 650 Linear Programming Applications Chapter

Lecture 2 MGMT 650 Linear Programming Applications Chapter 4

Possible Outcomes of a LP (Section 2. 6) · A LP is either Infeasible – there exists no solution which satisfies all constraints and optimizes the objective function · or, Unbounded – increase/decrease objective function as much as you like without violating any constraint · or, Has an Optimal Solution · · · Optimal values of decision variables Optimal objective function value 2

Infeasible LP – An Example minimize 4 x 11+7 x 12+7 x 13+x 14+12 x 21+3 x 22+8 x 23+8 x 24+8 x 31+10 x 32+16 x 33+5 x 34 Subject to · x 11+x 12+x 13+x 14=100 · x 21+x 22+x 23+x 24=200 · x 31+x 32+x 33+x 34=150 · · x 11+x 21+x 31=80 x 12+x 22+x 32=90 x 13+x 23+x 33=120 x 14+x 24+x 34=170 · xij>=0, i=1, 2, 3; j=1, 2, 3, 4 · · · Total demand exceeds total supply 3

Unbounded LP – An Example maximize 2 x 1 + x 2 subject to -x 1 + x 2 1 x 1 - 2 x 2 2 x 1 , x 2 0 x 2 can be increased indefinitely without violating any constraint => Objective function value can be increased indefinitely 4

Multiple Optima – An Example maximize x 1 + 0. 5 x 2 subject to 2 x 1 + x 2 4 x 1 + 2 x 2 3 x 1 , x 2 0 • x 1= 2, x 2=0, objective function = 2 • x 1= 5/3, x 2=2/3, objective function = 2 5

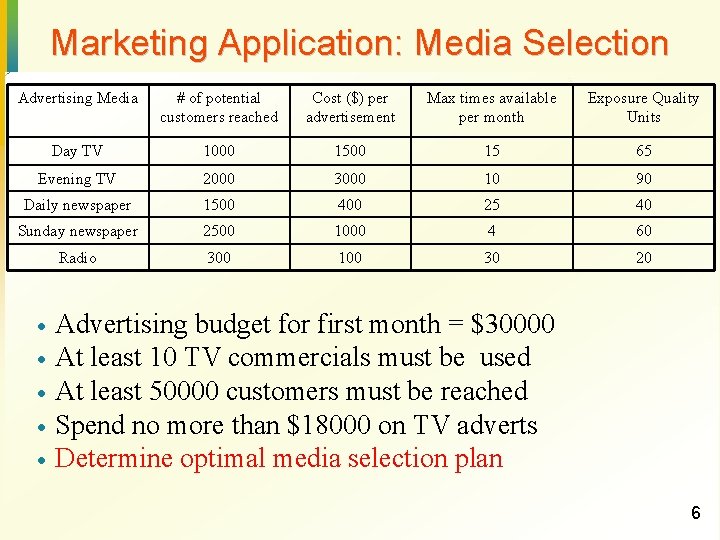
Marketing Application: Media Selection Advertising Media # of potential customers reached Cost ($) per advertisement Max times available per month Exposure Quality Units Day TV 1000 15 65 Evening TV 2000 3000 10 90 Daily newspaper 1500 400 25 40 Sunday newspaper 2500 1000 4 60 Radio 300 100 30 20 · · · Advertising budget for first month = $30000 At least 10 TV commercials must be used At least 50000 customers must be reached Spend no more than $18000 on TV adverts Determine optimal media selection plan 6

Media Selection Formulation · Step 1: Define decision variables · · · Step 2: Write the objective in terms of the decision variables · · DTV = # of day time TV adverts ETV = # of evening TV adverts DN = # of daily newspaper adverts SN = # of Sunday newspaper adverts R = # of radio adverts Maximize 65 DTV+90 ETV+40 DN+60 SN+20 R Step 3: Write the constraints in terms of the decision variables DTV ETV DN SN R + 25 <= 4 <= 30000 0 DN 25 SN 2 R 30 Exposure = 2370 units Availability of Media Budget + ETV >= 10 1500 DTV + 3000 ETV <= 18000 TV Constraints 1000 DTV + 2000 ETV >= 50000 Customers reached DTV, ETV, DN, SN, R >= 0 + 100 R <= ETV DTV 2500 SN + 10 10 3000 ETV + 1000 SN <= DTV + 1500 DN + 15 Value 1500 DTV + 400 DN <= Variable 300 R 7

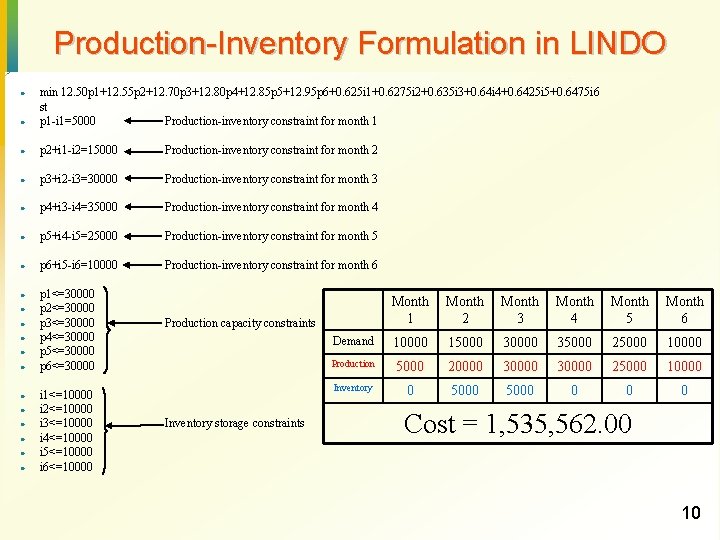
Production-Inventory Model · Nike produces footballs and must decide how many footballs to produce each month over the next 6 months Month 1 Month 2 Month 3 Month 4 Month 5 Month 6 Demand 10000 15000 30000 35000 25000 10000 Unit cost ($) 12. 50 12. 55 12. 70 12. 85 12. 95 · · · Starting inventory = 5000 Production capacity each month = 30000 footballs Storage capacity = 10000 footballs Inventory holding cost of a month = 5% of production cost of that month Determine production schedule that minimizes production and holding cost Assume for simplicity · · Production occurs continuously Demand occurs at month end 8

Production-Inventory Model Formulation · Step 1: define decision variables · · · Step 2: formulate objective function is terms of decision variables · · Pj = production quantity in month j Ij = end-of-month inventory in month j Sum of production cost + inventory holding cost Step 3: formulate objective function is terms of decision variables · Ij-1 + Pj = Dj + Ij · Pj < = 30000 · Ij <= 10000 · Pj, Ij >=0 9

Production-Inventory Formulation in LINDO · min 12. 50 p 1+12. 55 p 2+12. 70 p 3+12. 80 p 4+12. 85 p 5+12. 95 p 6+0. 625 i 1+0. 6275 i 2+0. 635 i 3+0. 64 i 4+0. 6425 i 5+0. 6475 i 6 st p 1 -i 1=5000 Production-inventory constraint for month 1 · p 2+i 1 -i 2=15000 Production-inventory constraint for month 2 · p 3+i 2 -i 3=30000 Production-inventory constraint for month 3 · p 4+i 3 -i 4=35000 Production-inventory constraint for month 4 · p 5+i 4 -i 5=25000 Production-inventory constraint for month 5 · p 6+i 5 -i 6=10000 Production-inventory constraint for month 6 · p 1<=30000 p 2<=30000 p 3<=30000 p 4<=30000 p 5<=30000 p 6<=30000 · · · i 1<=10000 i 2<=10000 i 3<=10000 i 4<=10000 i 5<=10000 i 6<=10000 Month 1 Month 2 Month 3 Month 4 Month 5 Month 6 Demand 10000 15000 30000 35000 25000 10000 Production 5000 20000 30000 25000 10000 Inventory 0 5000 0 Production capacity constraints Inventory storage constraints Cost = 1, 535, 562. 00 10

Blending Problem – Self-study · · Ferdinand Feed Company receives four raw grains from which it blends its dry pet food. The pet food advertises that each 8 -ounce packet meets the minimum daily requirements for vitamin C, protein and iron. The cost of each raw grain as well as the vitamin C, protein, and iron units per pound of each grain are as follows: Ferdinand is interested in producing the 8 -ounce mixture at minimum cost while meeting the minimum daily requirements of 6 units of vitamin C, 5 units of protein, and 5 units of iron. 11

Blending Problem Formulation Define the decision variables xj = the pounds of grain j (j = 1, 2, 3, 4) used in the 8 -ounce mixture · Define the objective function in terms of decision variables Minimize the total cost for an 8 -ounce mixture: MIN. 75 x 1 +. 90 x 2 +. 80 x 3 +. 70 x 4 · 12

Blending Problem - Constraints · Define the constraints Total weight of the mix is 8 -ounces (. 5 pounds): (1) x 1 + x 2 + x 3 + x 4 =. 5 Total amount of Vitamin C in the mix is at least 6 units: (2) 9 x 1 + 16 x 2 + 8 x 3 + 10 x 4 >= 6 Total amount of protein in the mix is at least 5 units: (3) 12 x 1 + 10 x 2 + 10 x 3 + 8 x 4 >= 5 Total amount of iron in the mix is at least 5 units: (4) 14 x 2 + 15 x 3 + 7 x 4 >= 5 Nonnegativity of variables: xj > 0 for all j 13

Blending Problem – Optimal Solution OBJECTIVE FUNCTION VALUE = · · · VARIABLE VALUE X 1 0. 099 X 2 0. 213 X 3 0. 088 X 4 0. 099 Thus, the optimal blend is about. 10 lb. of grain 1, . 21 lb. of grain 2, . 09 lb. of grain 3, and. 10 lb. of grain 4. The mixture costs 40. 6 cents. 0. 406 REDUCED COSTS 0. 000 14

Transportation Problem – Chapter 7 · Objective: · · · determination of a transportation plan of a single commodity from a number of sources to a number of destinations, such that total cost of transportation is minimized Sources may be plants, destinations may be warehouses Question: · · · how many units to transport from source i to destination j such that supply and demand constraints are met, and total transportation cost is minimized 15

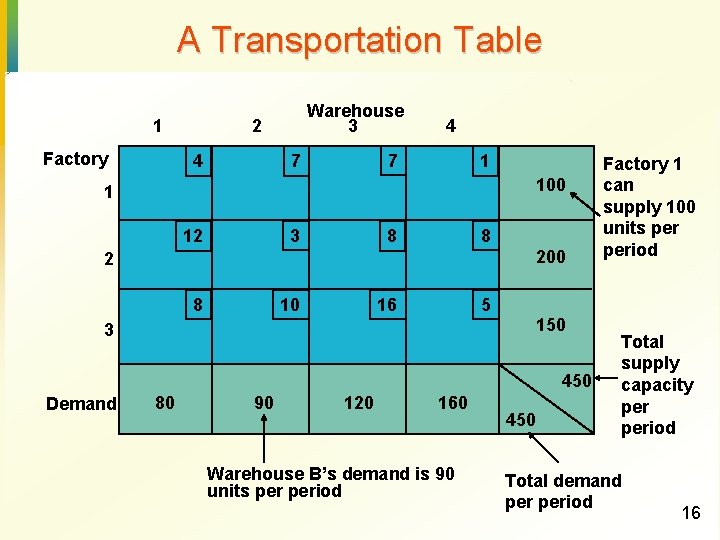
A Transportation Table 1 Factory Warehouse 3 2 4 4 7 7 1 100 1 3 12 8 8 200 2 10 8 16 5 150 3 450 Demand 80 90 120 Factory 1 can supply 100 units period 160 Warehouse B’s demand is 90 units period 450 Total supply capacity period Total demand period 16

LP Formulation of Transportation Problem · minimize 4 x 11+7 x 12+7 x 13+x 14+12 x 21+3 x 22+8 x 23+8 x 24+8 x 31+10 x 32+ 16 x 33+5 x 34 Subject to Minimize total cost of transportation · x 11+x 12+x 13+x 14=100 Supply constraint for factories · x 21+x 22+x 23+x 24=200 · x 31+x 32+x 33+x 34=150 · x 11+x 21+x 31=80 · x 12+x 22+x 32=90 Demand constraint of warehouses · x 13+x 23+x 33=120 · x 14+x 24+x 34=160 · xij>=0, i=1, 2, 3; j=1, 2, 3, 4 17

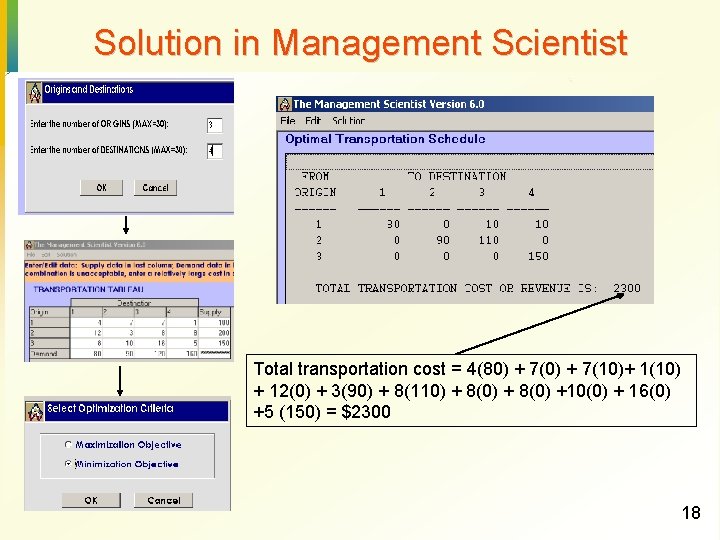
Solution in Management Scientist Total transportation cost = 4(80) + 7(10)+ 1(10) + 12(0) + 3(90) + 8(110) + 8(0) +10(0) + 16(0) +5 (150) = $2300 18

Assignment Problem – Chapter 7 · Special case of transportation problem When # of rows = # of columns in the transportation tableau · All supply and demands =1 · Objective: Assign n jobs/workers to n machines such that the total cost of assignment is minimized · Plenty of practical applications · Job shops · Hospitals · Airlines, etc. · 19

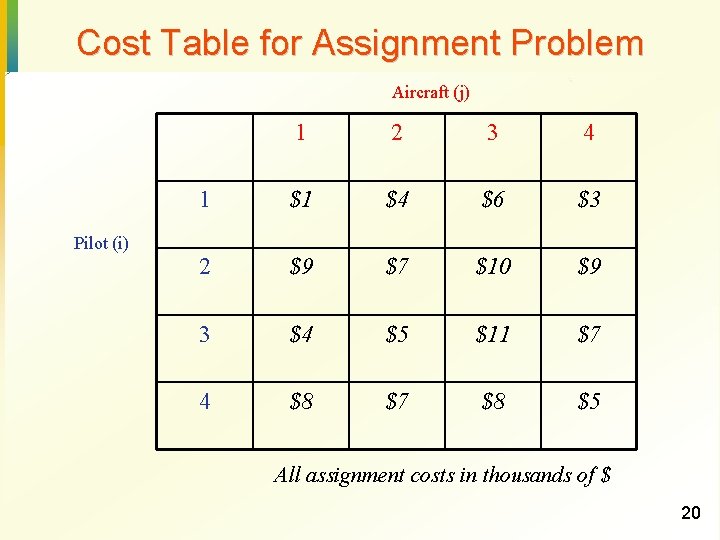
Cost Table for Assignment Problem Aircraft (j) Pilot (i) 1 2 3 4 1 $1 $4 $6 $3 2 $9 $7 $10 $9 3 $4 $5 $11 $7 4 $8 $7 $8 $5 All assignment costs in thousands of $ 20

Formulation of Assignment Problem minimize x 11+4 x 12+6 x 13+3 x 14 + 9 x 21+7 x 22+10 x 23+9 x 24 + 4 x 31+5 x 32+11 x 33+7 x 34 + 8 x 41+7 x 42+8 x 43+5 x 44 subject to Pilot Assigned to Cost · x 11+x 12+x 13+x 14=1 aircraft # (`000 $) · x 21+x 22+x 23+x 24=1 1 · x 31+x 32+x 33+x 34=1 · x 41+x 42+x 43+x 44=1 2 3 10 · · · x 11+x 21+x 31+x 41=1 x 12+x 22+x 32+x 42=1 x 13+x 23+x 33+x 43=1 x 14+x 24+x 34+x 44=1 3 4 2 4 5 5 Optimal Solution: x 11=1; x 23=1; x 32=1; x 44=1; rest=0 Cost of assignment = 1+10+5+5=$21 (`000) xij = 1, if pilot i is assigned to aircraft j, i=1, 2, 3, 4; j=1, 2, 3, 4 0 otherwise 21

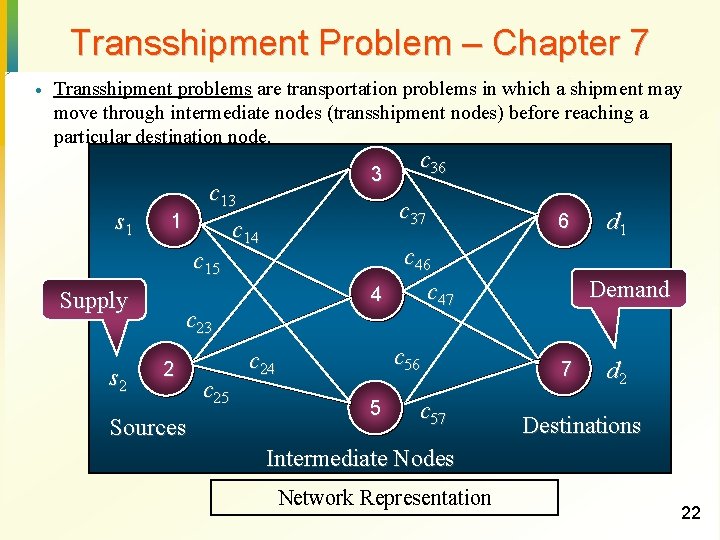
Transshipment Problem – Chapter 7 · Transshipment problems are transportation problems in which a shipment may move through intermediate nodes (transshipment nodes) before reaching a particular destination node. s 1 c 13 1 c 15 Supply s 2 3 c 37 c 14 Sources c 25 6 c 47 4 c 23 2 c 36 c 56 c 24 5 c 57 d 1 Demand 7 d 2 Destinations Intermediate Nodes Network Representation 22

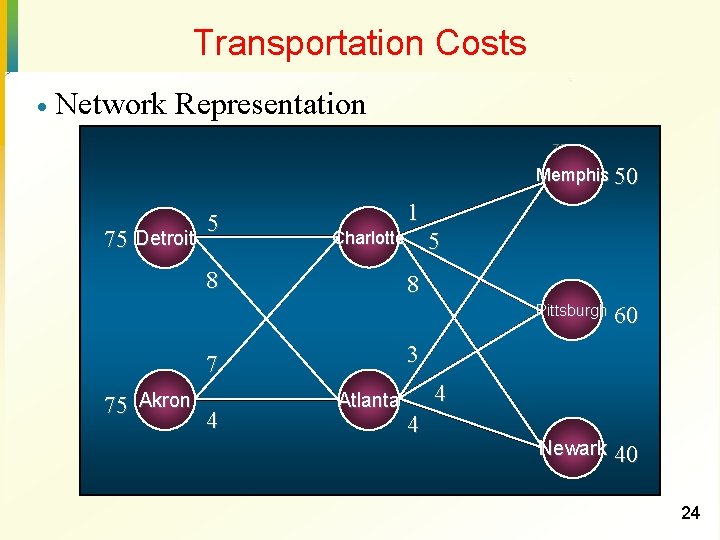
Example: Goodyear Tires The Detroit (1) and Akron (2) facilities of Goodyear supply three customers at Memphis, Pittsburgh, and Newark. · Distribution is done through warehouses located at Charlotte (3) and Atlanta (4). · Current weekly demands by the customers are 50, 60 and 40 units for Memphis (5), Pittsburgh (6), and Newark (7) respectively. · Both facilities at Detroit and Akron can supply at most 75 units per week. · 23

Transportation Costs · Network Representation ZROX Memphis 50 ARNOLD 75 Detroit 5 1 8 8 4 Pittsburgh HEWES 60 Newark 40 3 7 75 Akron 5 Charlotte WASH Atlanta BURN 4 4 24

Goodyear Tires Formulation · Define Decision Variables · · xij = amount shipped from manufacturer i to warehouse j xjk = amount shipped from warehouse j to customer k · where · · i = 1 (Detroit), i = 2 (Akron), j = 3 (Charlotte), j = 4 (Atlanta), k = 5 (Memphis), k = 6 (Pittsburgh), k = 7 (Newark) Define Objective Function Minimize Overall Shipping Costs: Min 5 x 13 + 8 x 14 + 7 x 23 + 4 x 24 + 1 x 35 + 5 x 36 + 8 x 37 + 3 x 45 + 4 x 46 + 4 x 47 25

Goodyear Tires Formulation · Define Constraints Amount Out of Detroit: x 13 + x 14 < 75 Amount Out of Akron: x 23 + x 24 < 75 Amount Through Charlotte: x 13 + x 23 - x 35 - x 36 - x 37 = 0 Amount Through Atlanta: x 14 + x 24 - x 45 - x 46 - x 47 = 0 Amount Into Memphis: x 35 + x 45 = 50 Amount Into Pittsburgh: x 36 + x 46 = 60 Amount Into Newark: x 37 + x 47 = 40 Non-negativity of variables: xij , xjk > 0, for all i, j and k. 26

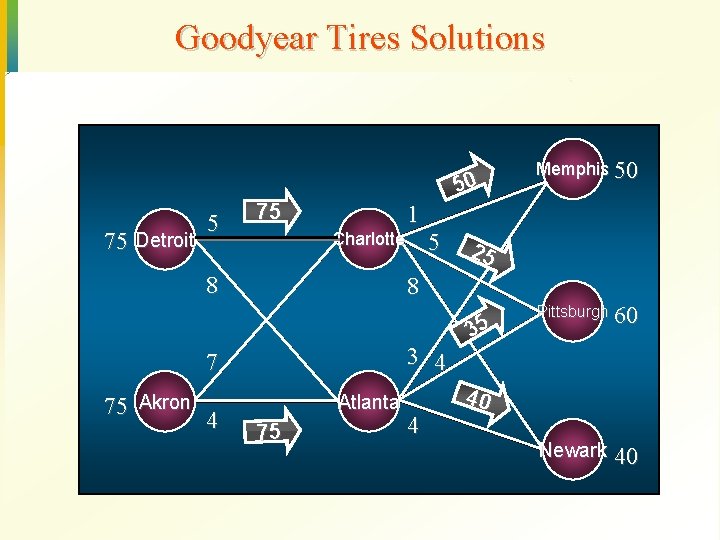
Goodyear Tires Solutions Objective Function Value = Variable X 13 X 14 X 23 X 24 X 35 X 36 X 37 X 45 X 46 X 47 Value 75. 000 0. 000 75. 000 50. 000 25. 000 0. 000 35. 000 40. 000 1150. 000 Reduced Costs 0. 000 2. 000 4. 000 0. 000 3. 000 0. 000

Goodyear Tires Solutions ZROX 50 ARNOLD 75 Detroit 5 75 1 25 8 3 4 7 4 5 Charlotte 8 75 Akron Memphis 50 75 WASH Atlanta BURN 4 35 Pittsburgh HEWES 60 Newark 40 40