Lecture 15 Rotational Dynamics Moment of Inertia The

Lecture 15 Rotational Dynamics

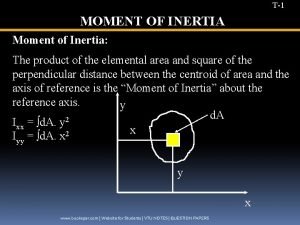
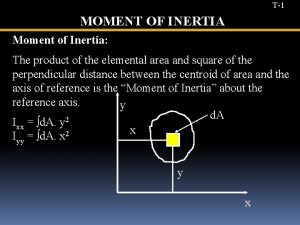
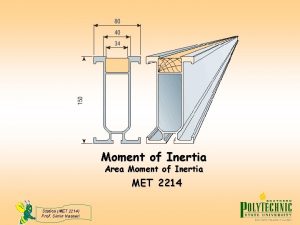
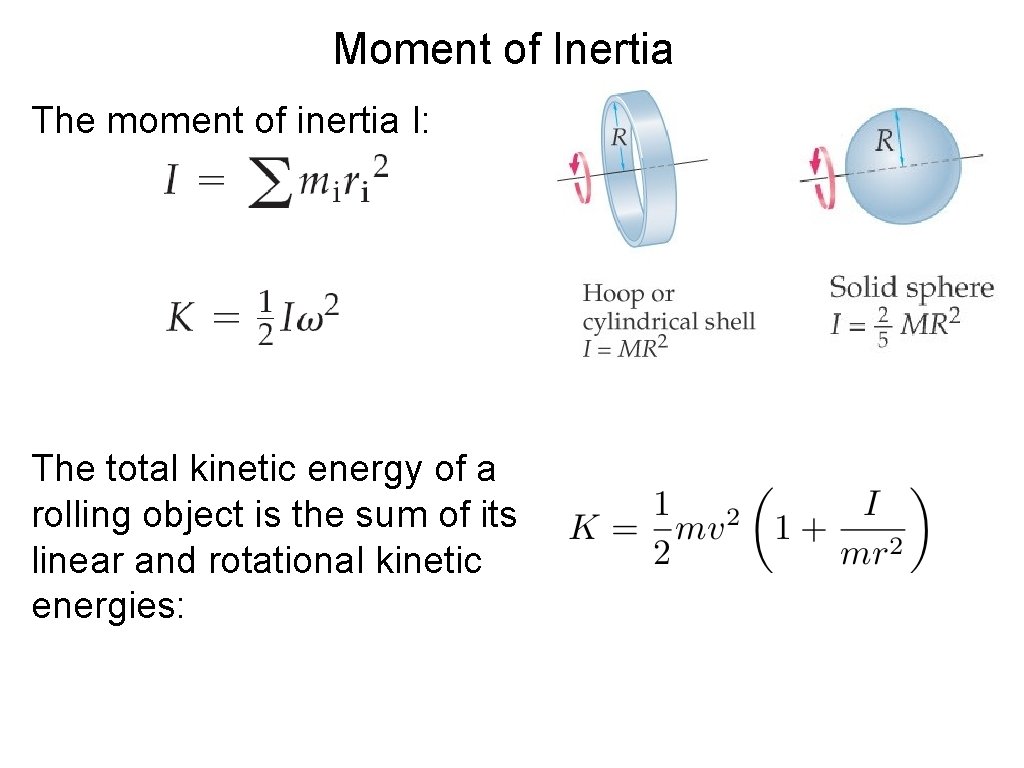
Moment of Inertia The moment of inertia I: The total kinetic energy of a rolling object is the sum of its linear and rotational kinetic energies:

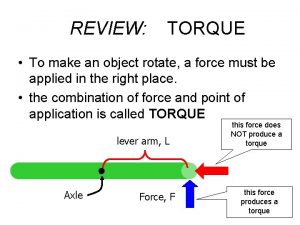
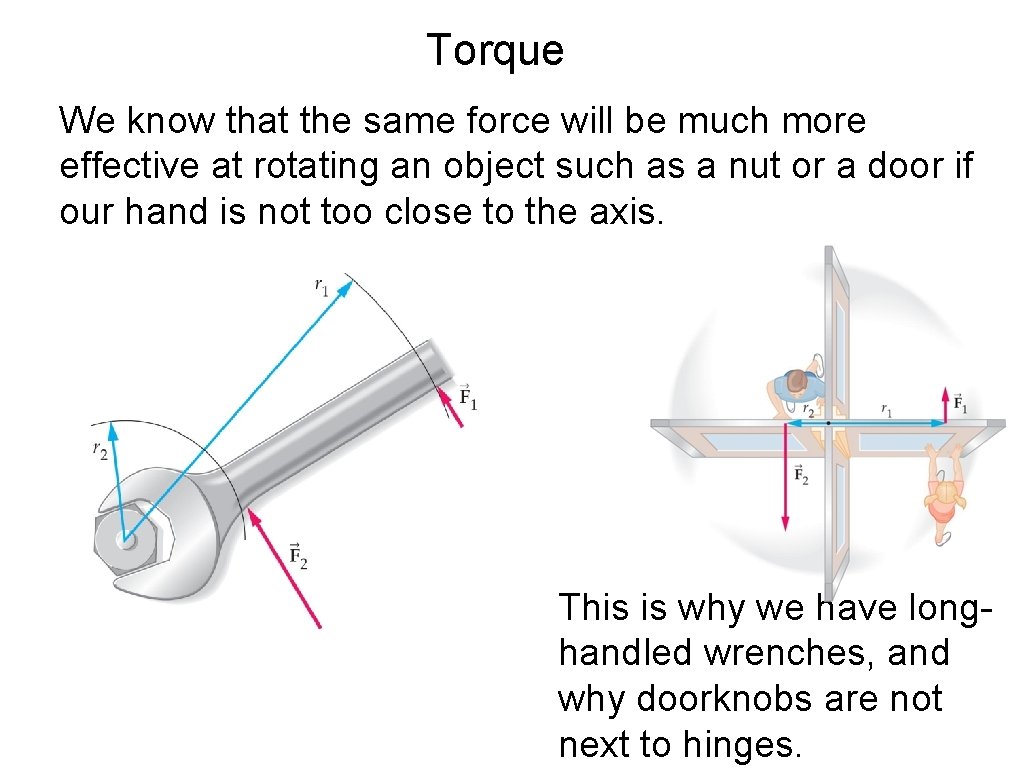
Torque We know that the same force will be much more effective at rotating an object such as a nut or a door if our hand is not too close to the axis. This is why we have longhandled wrenches, and why doorknobs are not next to hinges.

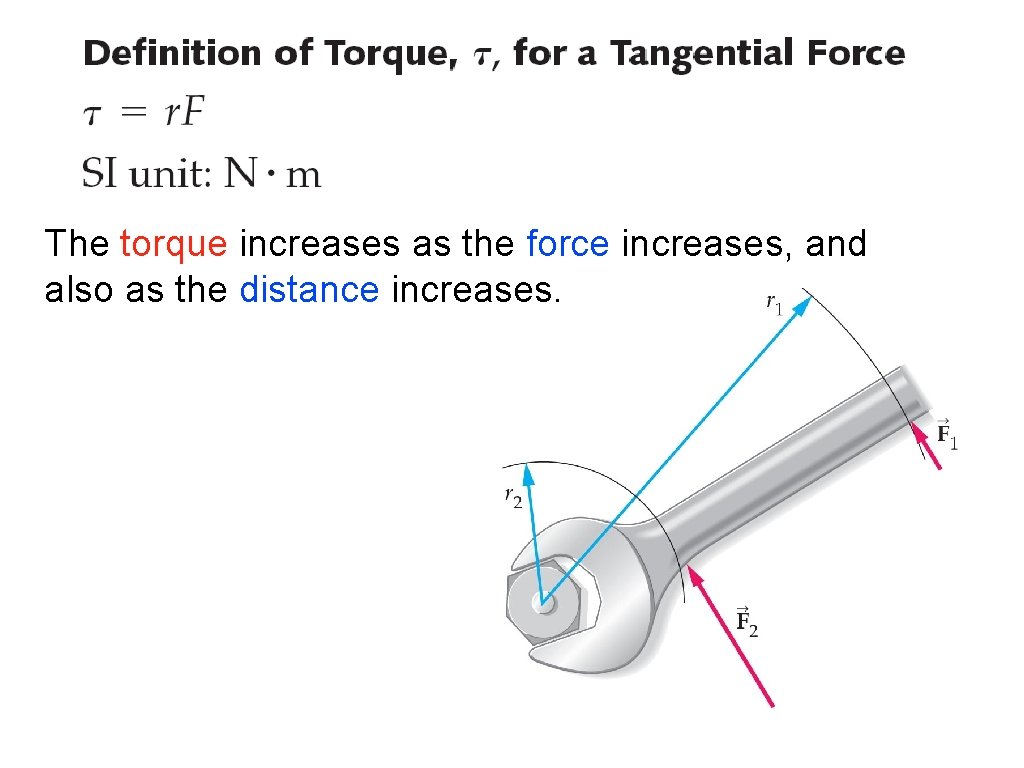
The torque increases as the force increases, and also as the distance increases.

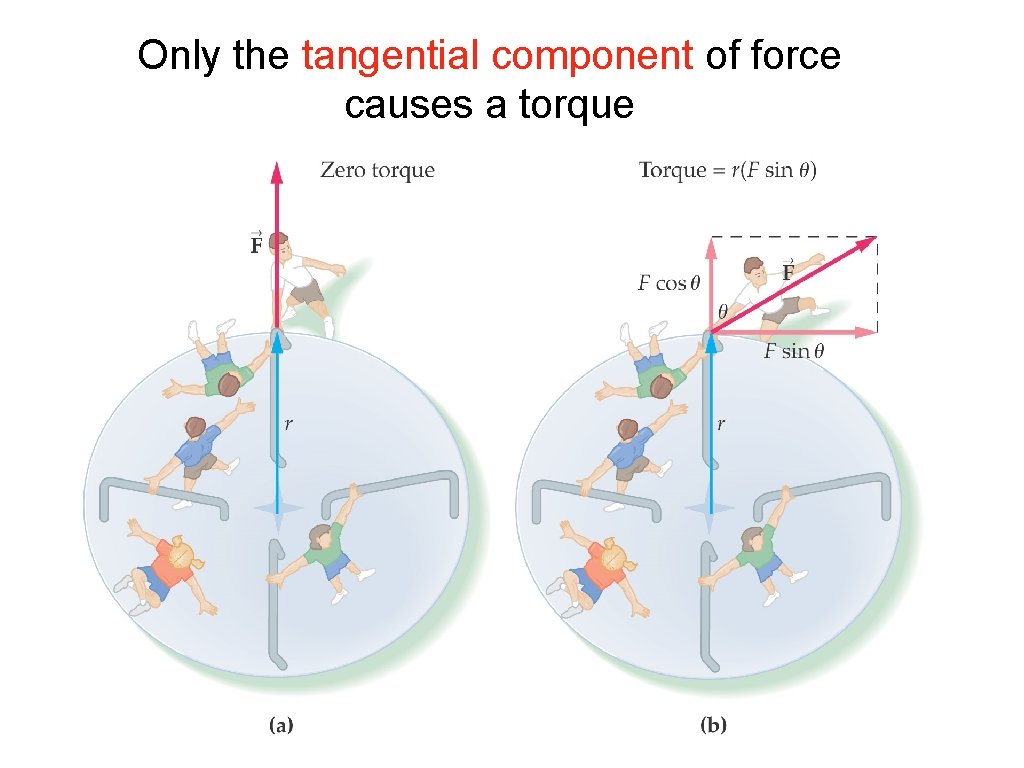
Only the tangential component of force causes a torque

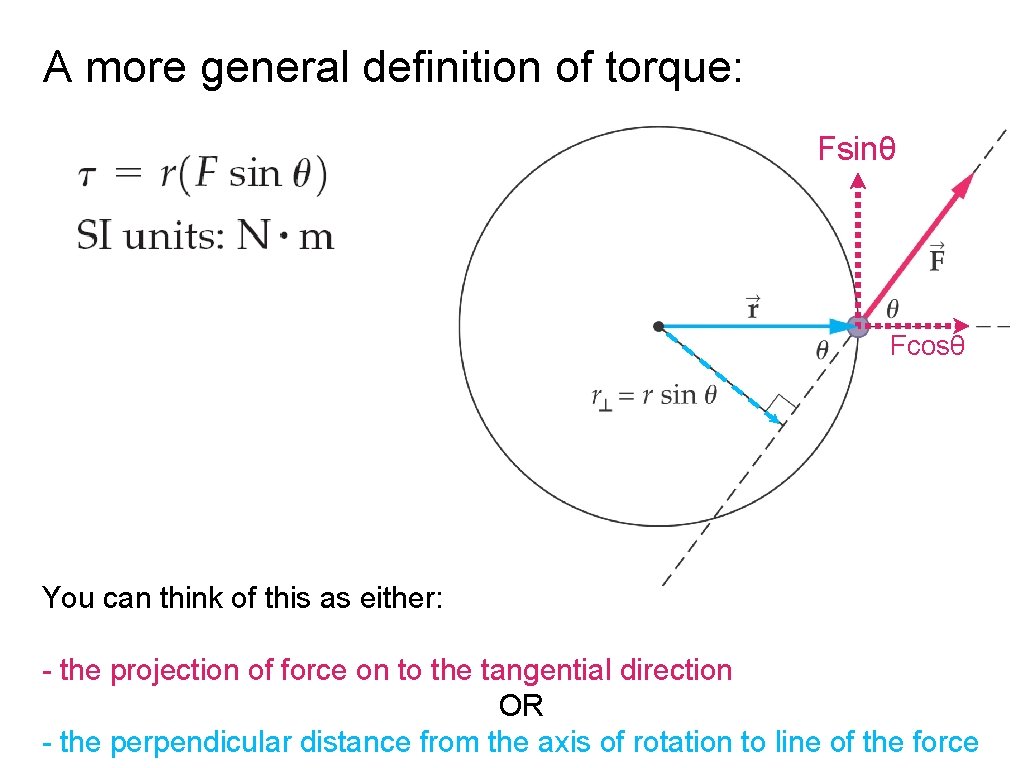
A more general definition of torque: Fsinθ Fcosθ You can think of this as either: - the projection of force on to the tangential direction OR - the perpendicular distance from the axis of rotation to line of the force

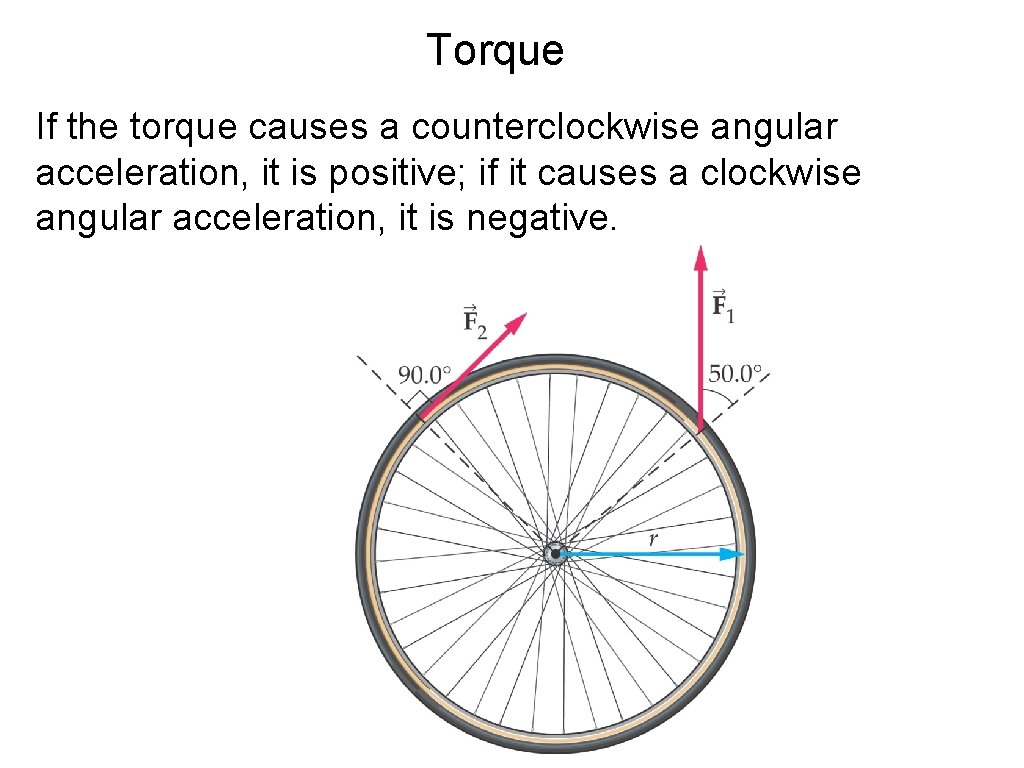
Torque If the torque causes a counterclockwise angular acceleration, it is positive; if it causes a clockwise angular acceleration, it is negative.

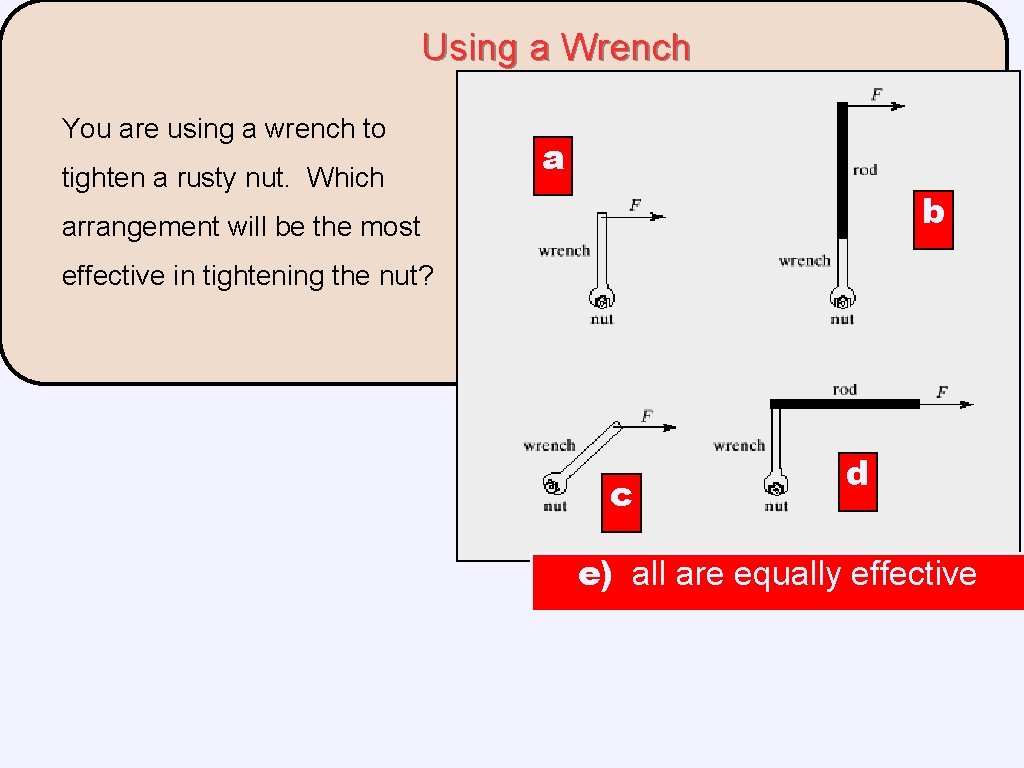
Using a Wrench You are using a wrench to tighten a rusty nut. Which a b arrangement will be the most effective in tightening the nut? c d e) all are equally effective

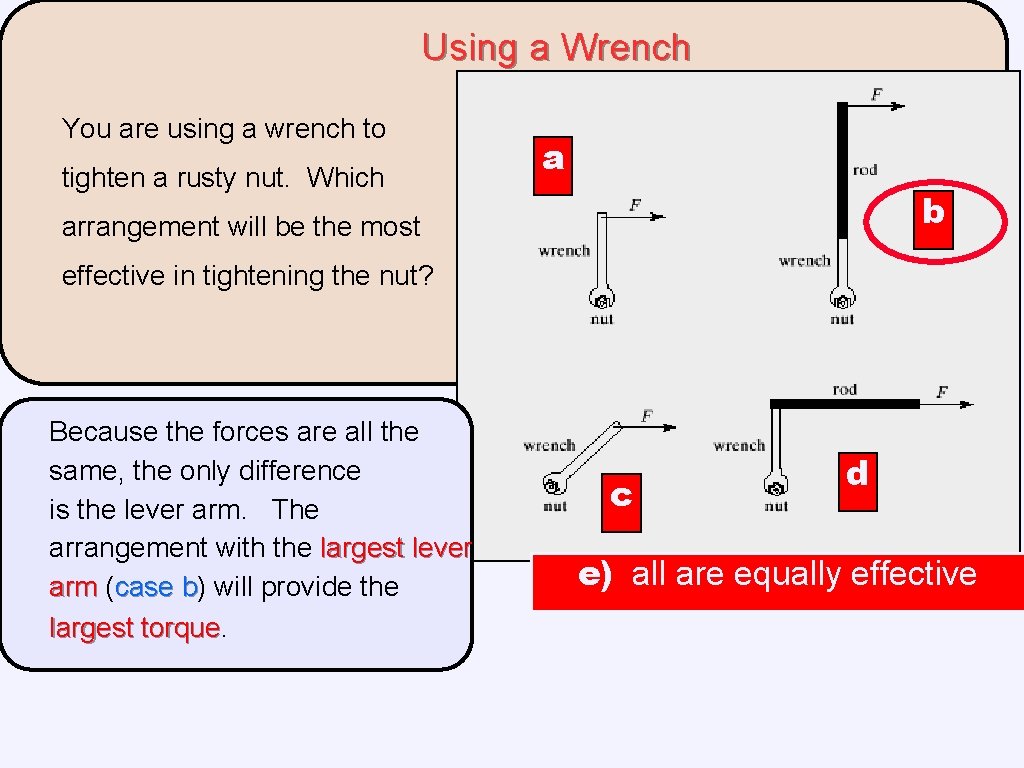
Using a Wrench You are using a wrench to tighten a rusty nut. Which a b arrangement will be the most effective in tightening the nut? Because the forces are all the same, the only difference is the lever arm. The arrangement with the largest lever arm (case b) b will provide the largest torque c d e) all are equally effective

The gardening tool shown is used to pull weeds. If a 1. 23 N-m torque is required to pull a given weed, what force did the weed exert on the tool? What force was used on the tool?

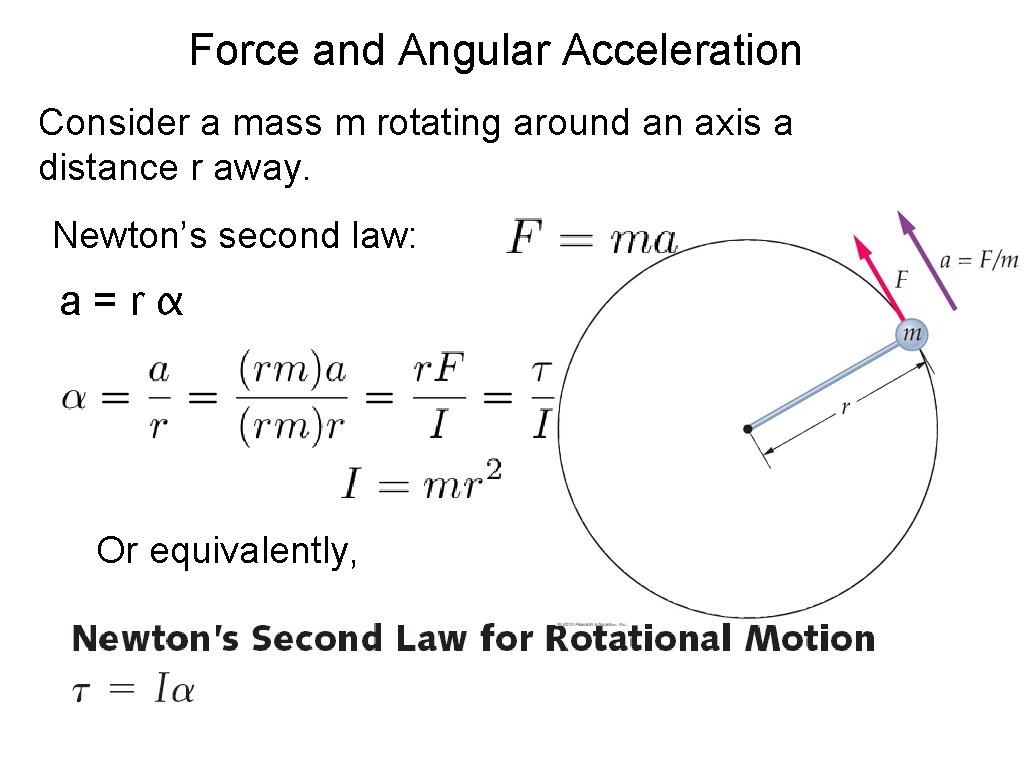
Force and Angular Acceleration Consider a mass m rotating around an axis a distance r away. Newton’s second law: a=rα Or equivalently,

Torque and Angular Acceleration Once again, we have analogies between linear and angular motion:

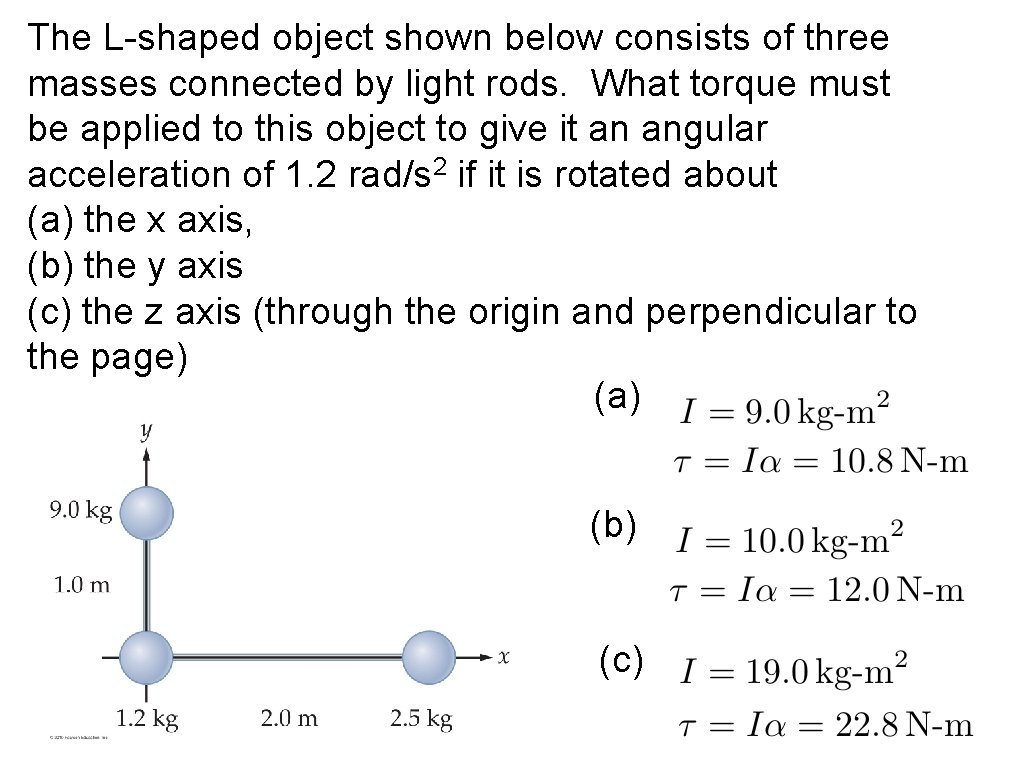
The L-shaped object shown below consists of three masses connected by light rods. What torque must be applied to this object to give it an angular acceleration of 1. 2 rad/s 2 if it is rotated about (a) the x axis, (b) the y axis (c) the z axis (through the origin and perpendicular to the page) (a) (b) (c)

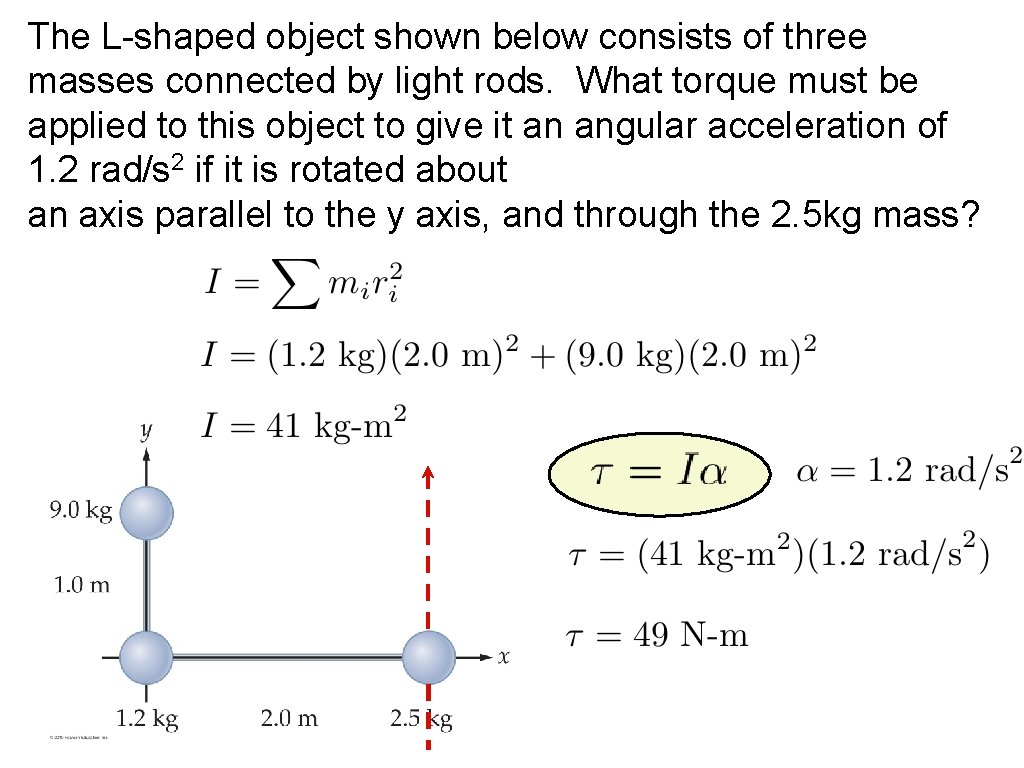
The L-shaped object shown below consists of three masses connected by light rods. What torque must be applied to this object to give it an angular acceleration of 1. 2 rad/s 2 if it is rotated about an axis parallel to the y axis, and through the 2. 5 kg mass?

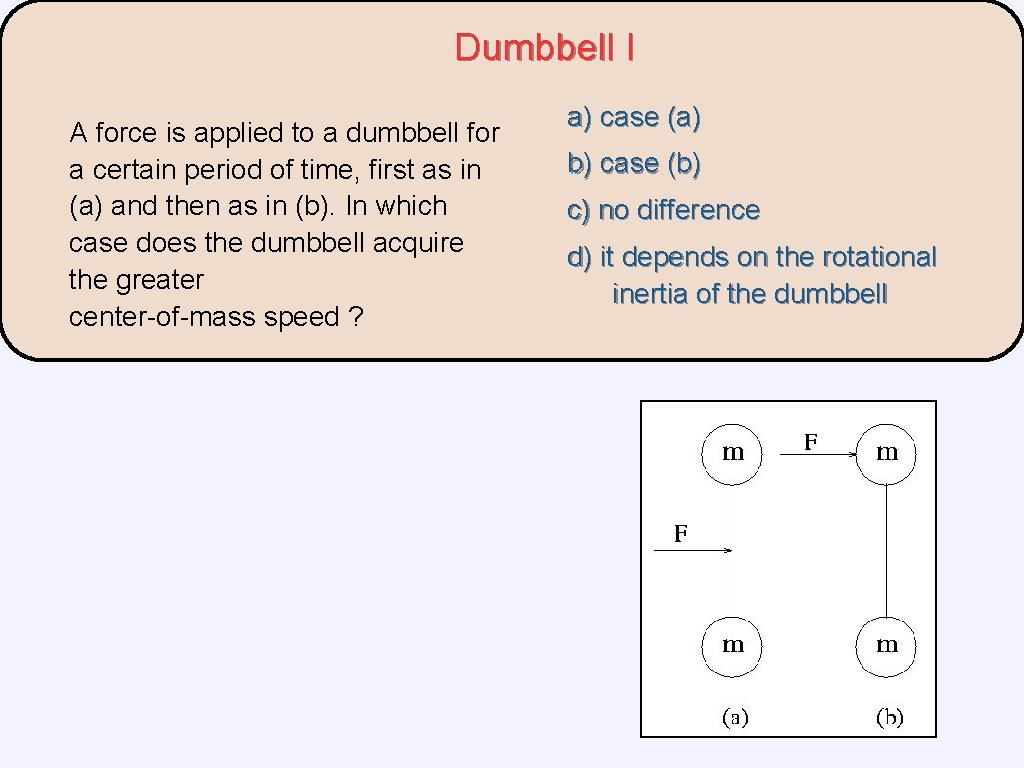
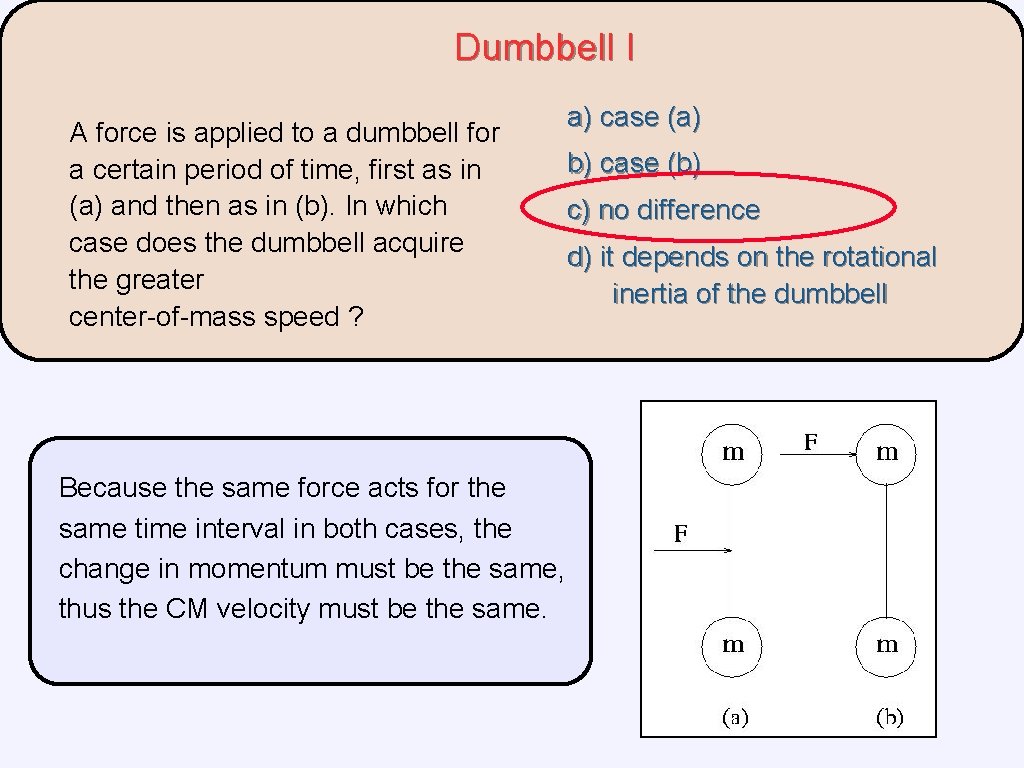
Dumbbell I A force is applied to a dumbbell for a certain period of time, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater center-of-mass speed ? a) case (a) b) case (b) c) no difference d) it depends on the rotational inertia of the dumbbell

Dumbbell I A force is applied to a dumbbell for a certain period of time, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater center-of-mass speed ? Because the same force acts for the same time interval in both cases, the change in momentum must be the same, thus the CM velocity must be the same. a) case (a) b) case (b) c) no difference d) it depends on the rotational inertia of the dumbbell

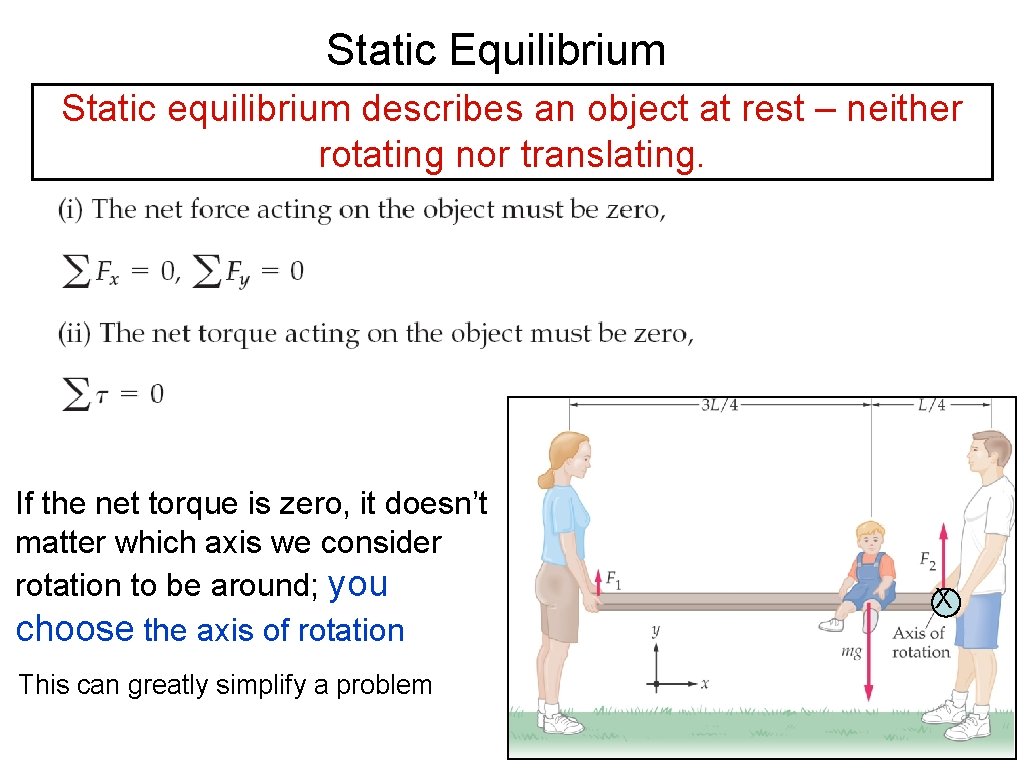
Static Equilibrium Static equilibrium describes an object at rest – neither rotating nor translating. If the net torque is zero, it doesn’t matter which axis we consider rotation to be around; you choose the axis of rotation This can greatly simplify a problem X

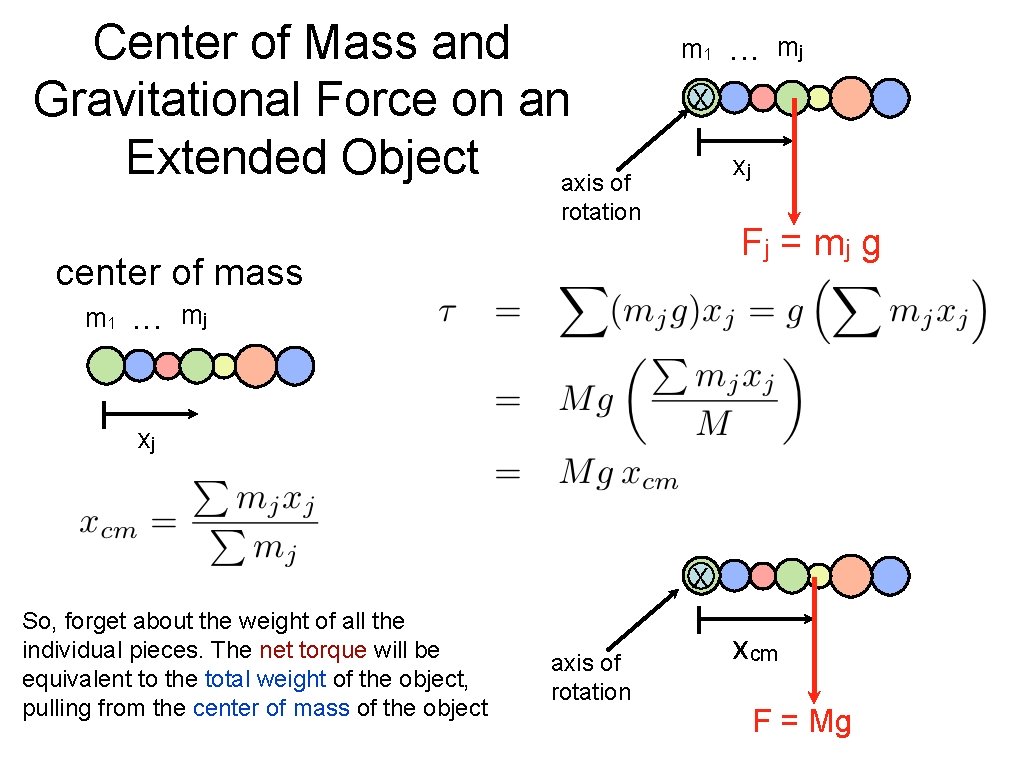
Center of Mass and Gravitational Force on an Extended Object axis of m 1 . . . mj X xj rotation Fj = m j g center of mass m 1. . . mj xj X So, forget about the weight of all the individual pieces. The net torque will be equivalent to the total weight of the object, pulling from the center of mass of the object axis of rotation xcm F = Mg

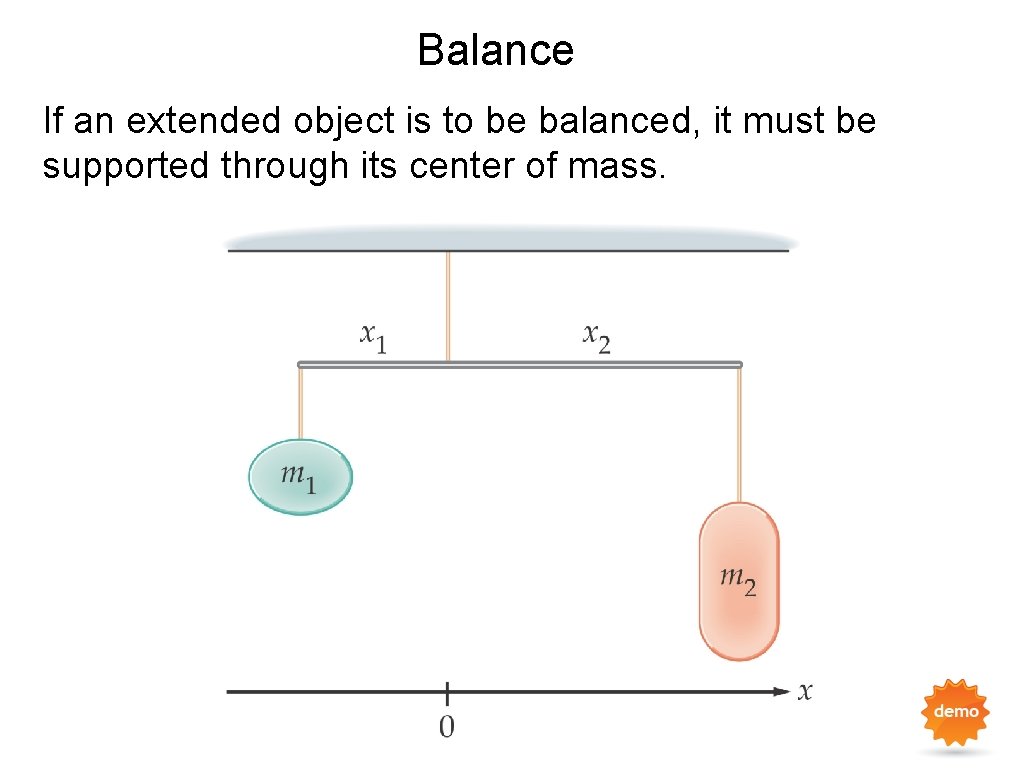
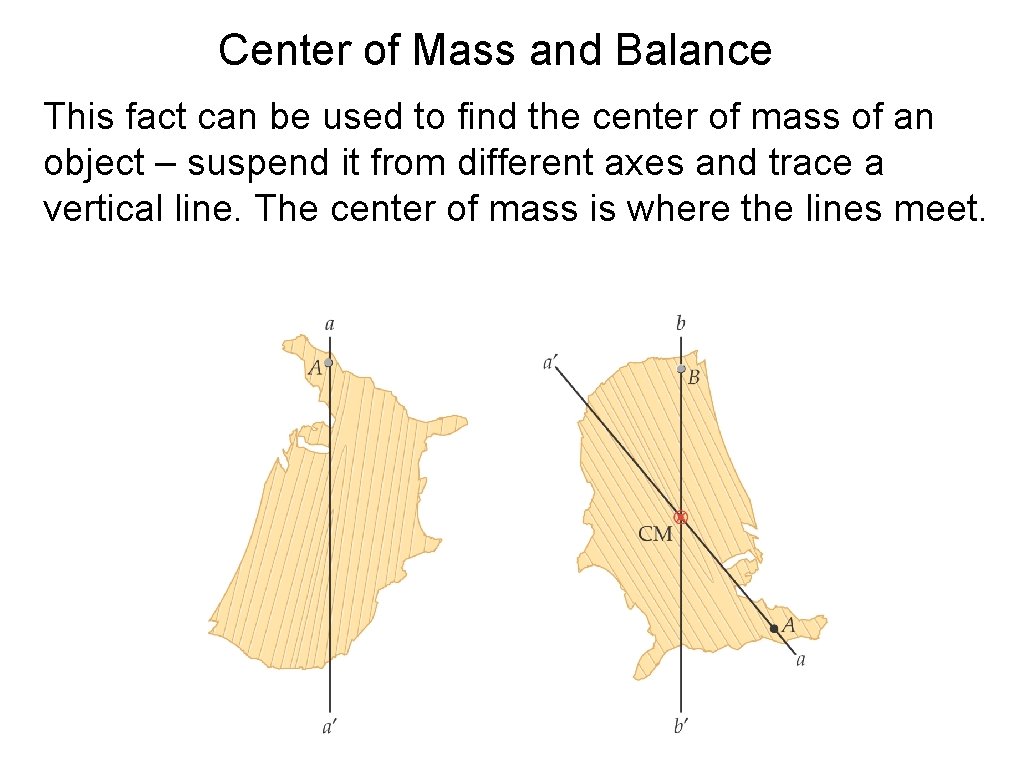
Balance If an extended object is to be balanced, it must be supported through its center of mass.

Center of Mass and Balance This fact can be used to find the center of mass of an object – suspend it from different axes and trace a vertical line. The center of mass is where the lines meet.

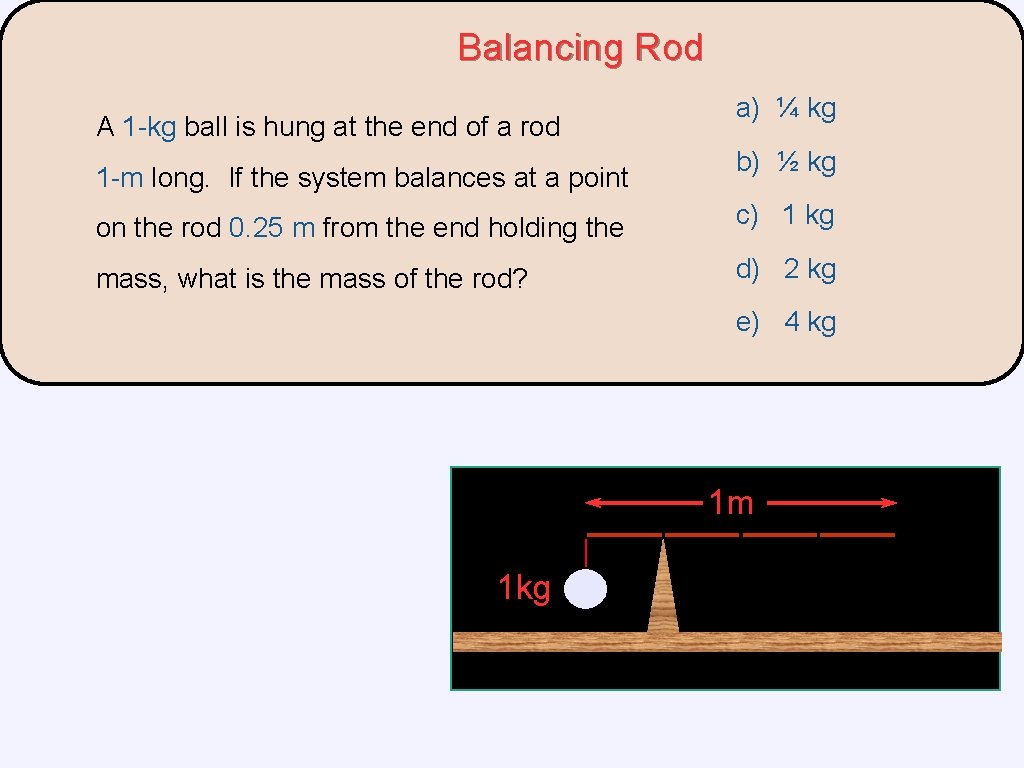
Balancing Rod A 1 -kg ball is hung at the end of a rod 1 -m long. If the system balances at a point a) ¼ kg b) ½ kg on the rod 0. 25 m from the end holding the c) 1 kg mass, what is the mass of the rod? d) 2 kg e) 4 kg 1 m 1 kg

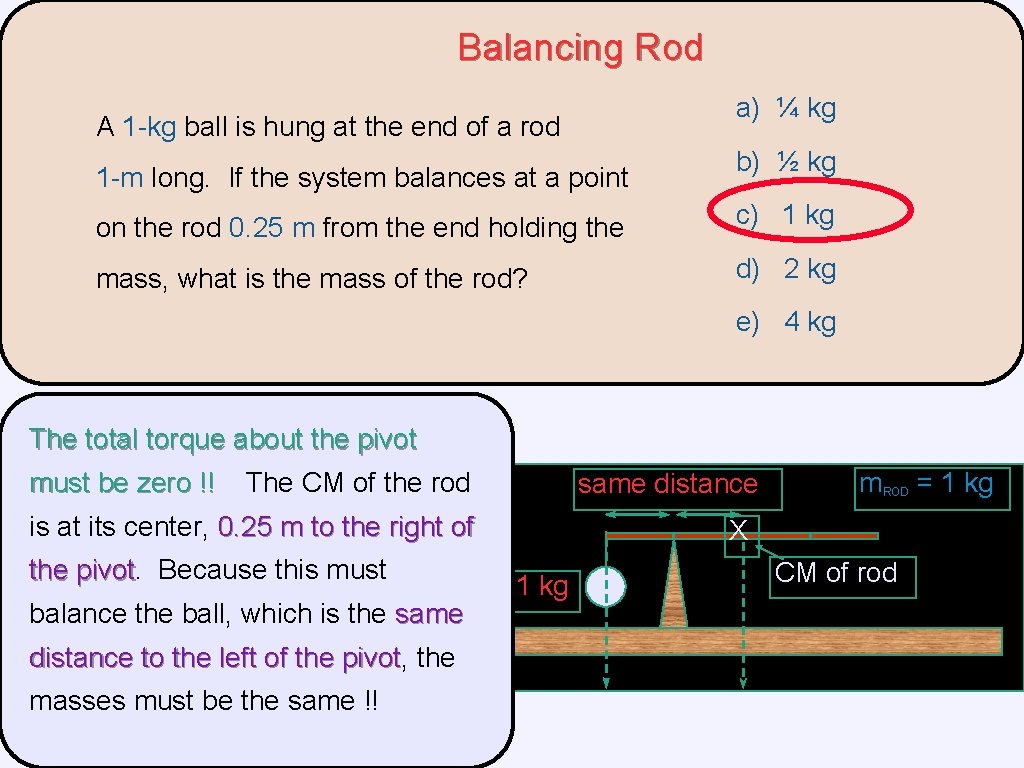
Balancing Rod a) ¼ kg A 1 -kg ball is hung at the end of a rod 1 -m long. If the system balances at a point b) ½ kg on the rod 0. 25 m from the end holding the c) 1 kg mass, what is the mass of the rod? d) 2 kg e) 4 kg The total torque about the pivot must be zero !! The CM of the rod same distance is at its center, 0. 25 m to the right of the pivot Because this must balance the ball, which is the same distance to the left of the pivot, pivot the masses must be the same !! m. ROD = 1 kg X 1 kg CM of rod

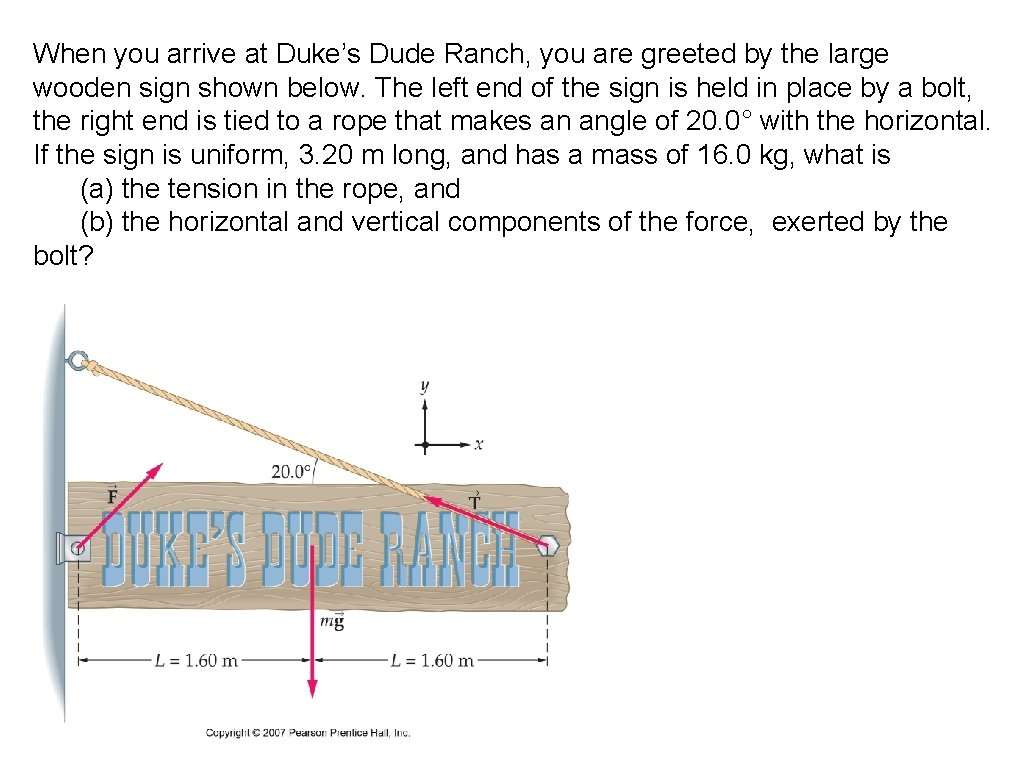
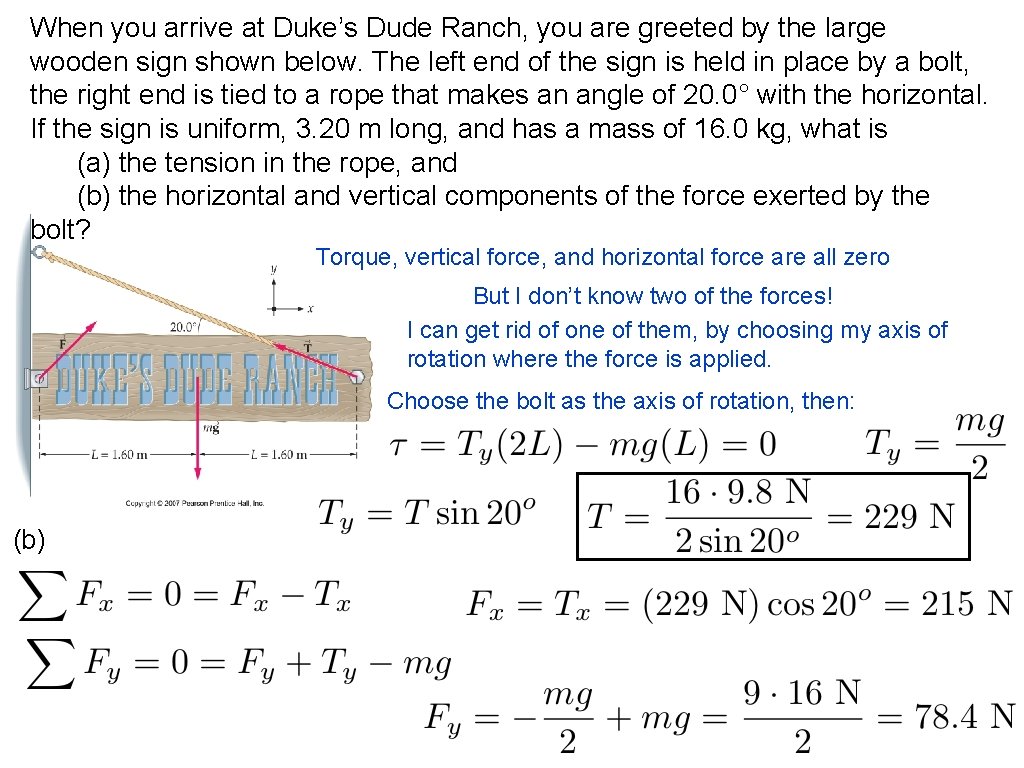
When you arrive at Duke’s Dude Ranch, you are greeted by the large wooden sign shown below. The left end of the sign is held in place by a bolt, the right end is tied to a rope that makes an angle of 20. 0° with the horizontal. If the sign is uniform, 3. 20 m long, and has a mass of 16. 0 kg, what is (a) the tension in the rope, and (b) the horizontal and vertical components of the force, exerted by the bolt?

When you arrive at Duke’s Dude Ranch, you are greeted by the large wooden sign shown below. The left end of the sign is held in place by a bolt, the right end is tied to a rope that makes an angle of 20. 0° with the horizontal. If the sign is uniform, 3. 20 m long, and has a mass of 16. 0 kg, what is (a) the tension in the rope, and (b) the horizontal and vertical components of the force exerted by the bolt? Torque, vertical force, and horizontal force are all zero But I don’t know two of the forces! I can get rid of one of them, by choosing my axis of rotation where the force is applied. Choose the bolt as the axis of rotation, then: (b)

F = ma implies Newton’s first law: without a force, there is no acceleration Now we have Linear momentum was the concept that tied together Newton’s Laws, is there something similar for rotational motion?

Angular and linear acceleration

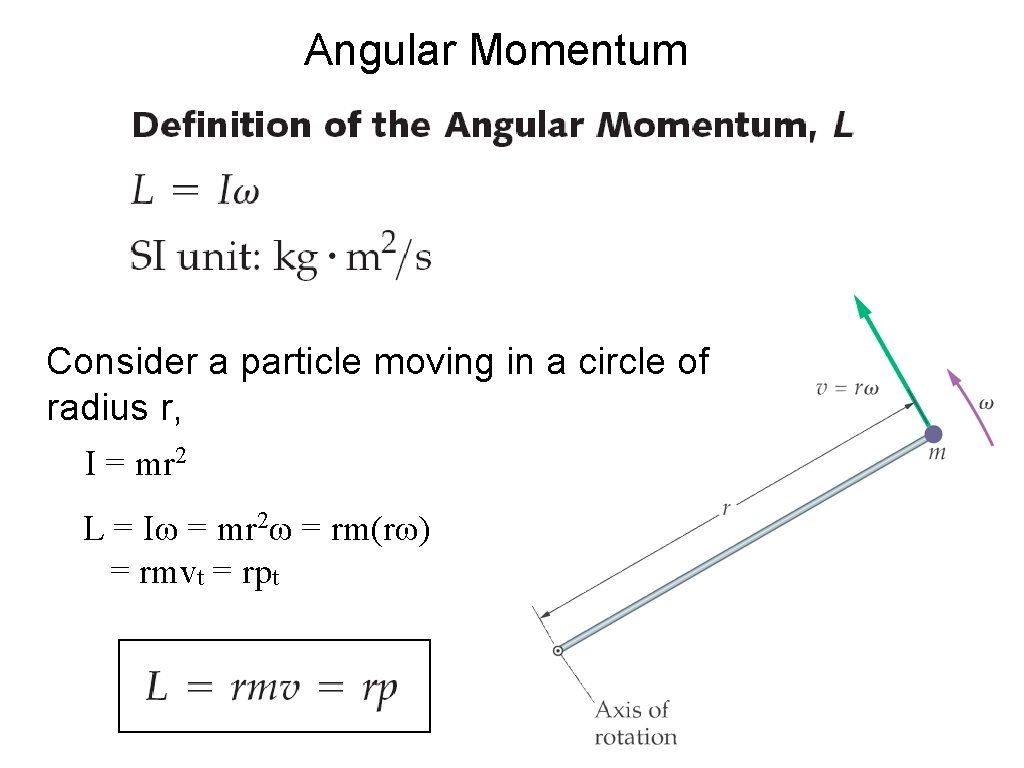
Angular Momentum Consider a particle moving in a circle of radius r, I = mr 2 L = Iω = mr 2ω = rm(rω) = rmvt = rpt

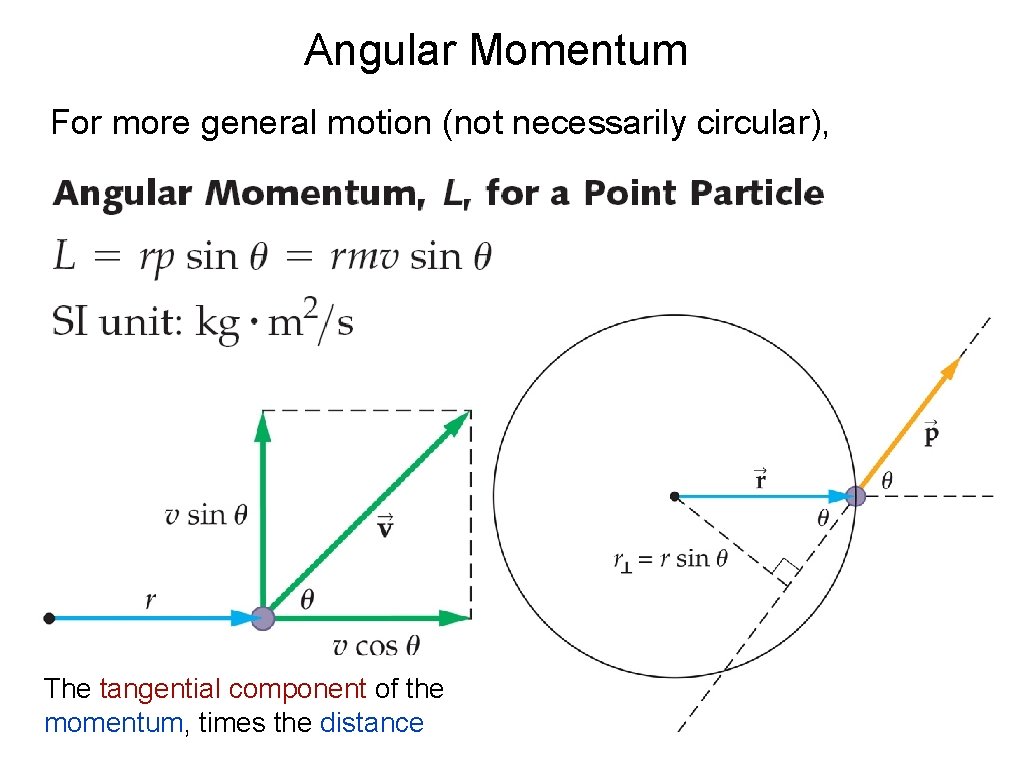
Angular Momentum For more general motion (not necessarily circular), The tangential component of the momentum, times the distance

Angular Momentum For an object of constant moment of inertia, consider the rate of change of angular momentum analogous to 2 nd Law for Linear Motion

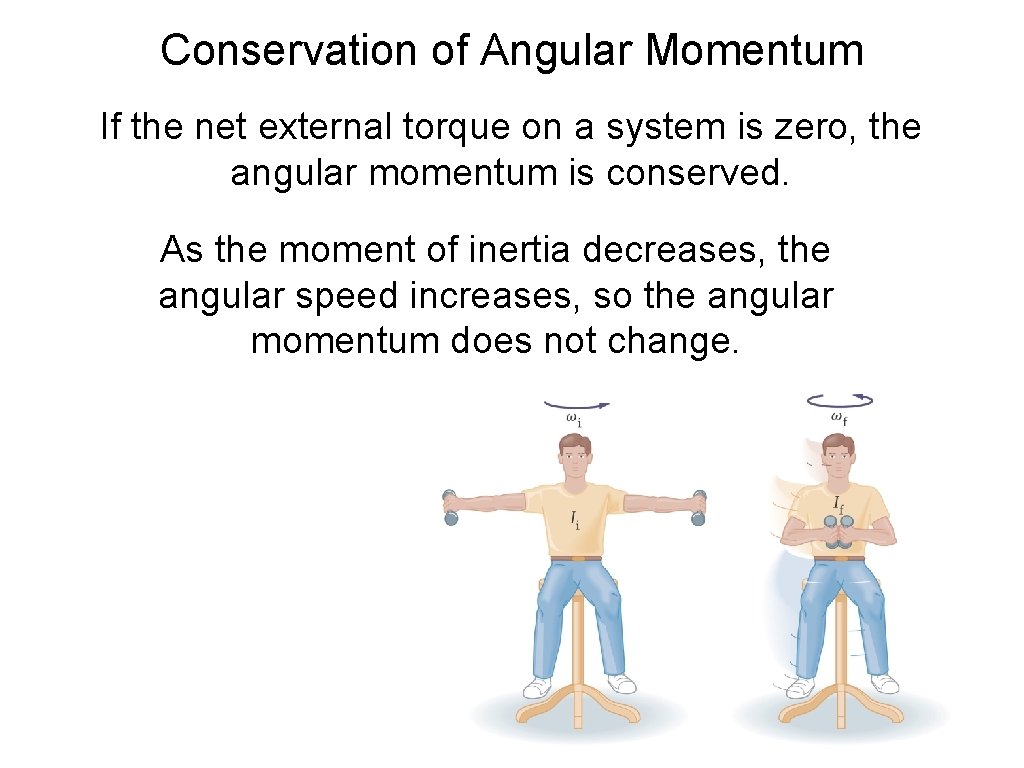
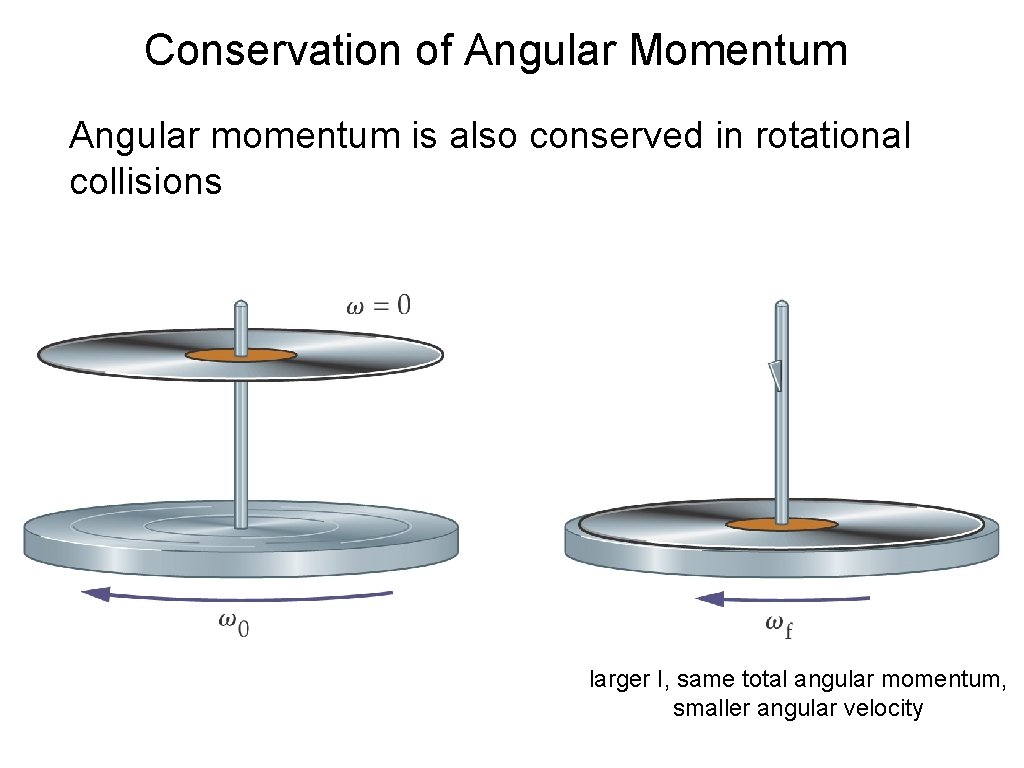
Conservation of Angular Momentum If the net external torque on a system is zero, the angular momentum is conserved. As the moment of inertia decreases, the angular speed increases, so the angular momentum does not change.

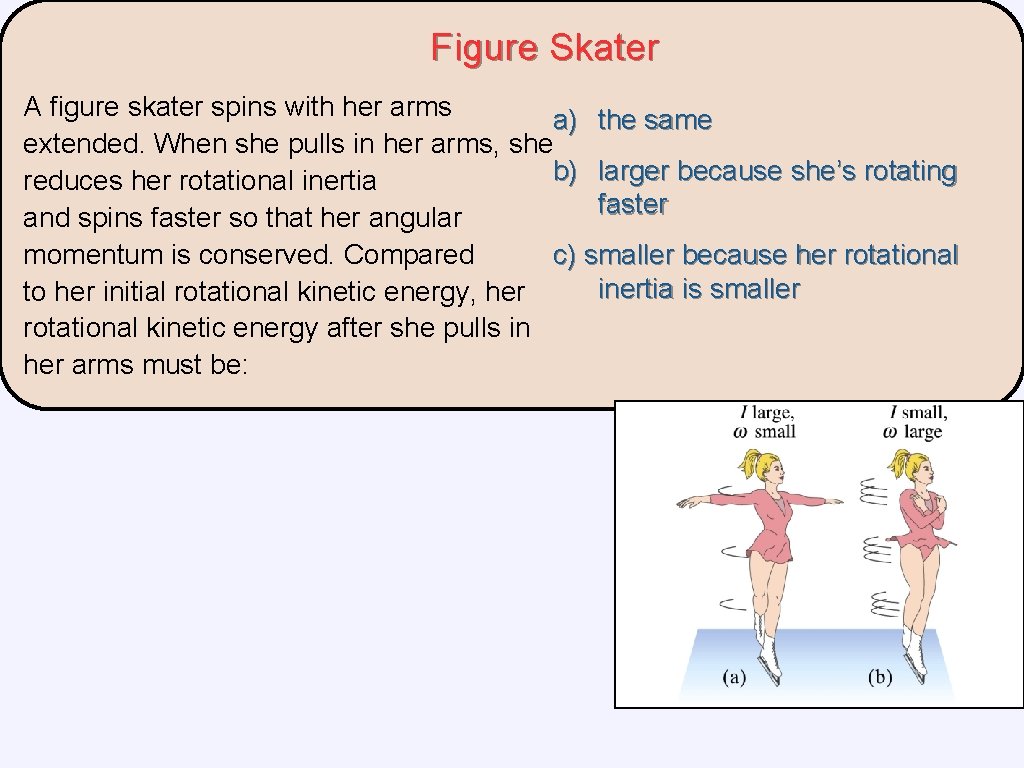
Figure Skater A figure skater spins with her arms a) the same extended. When she pulls in her arms, she b) larger because she’s rotating reduces her rotational inertia faster and spins faster so that her angular momentum is conserved. Compared c) smaller because her rotational inertia is smaller to her initial rotational kinetic energy, her rotational kinetic energy after she pulls in her arms must be:

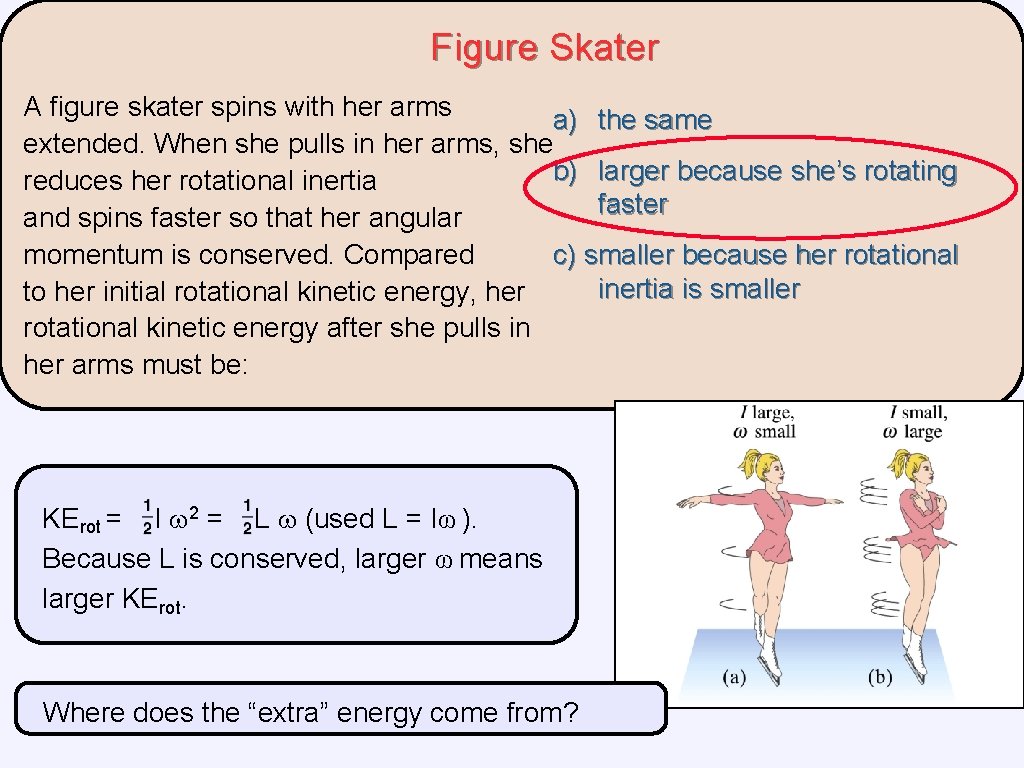
Figure Skater A figure skater spins with her arms a) the same extended. When she pulls in her arms, she b) larger because she’s rotating reduces her rotational inertia faster and spins faster so that her angular momentum is conserved. Compared c) smaller because her rotational inertia is smaller to her initial rotational kinetic energy, her rotational kinetic energy after she pulls in her arms must be: KErot = I 2 = L (used L = Iω ). Because L is conserved, larger ω means larger KErot. Where does the “extra” energy come from?

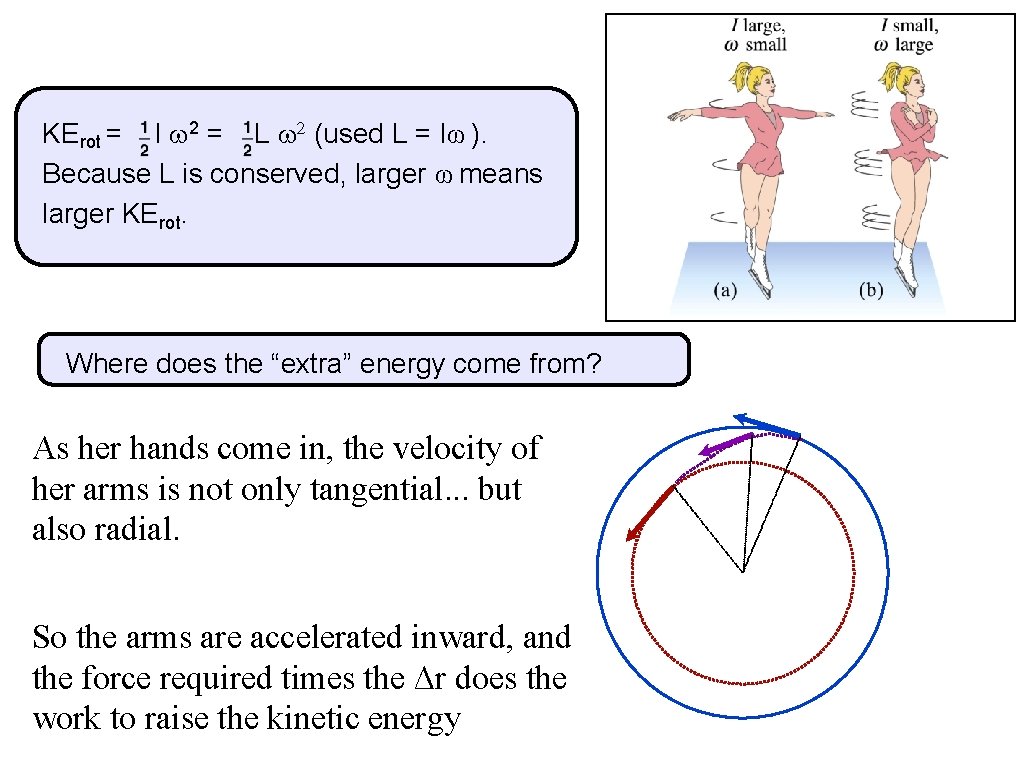
KErot = I 2 = L 2 (used L = Iω ). Because L is conserved, larger ω means larger KErot. Where does the “extra” energy come from? As her hands come in, the velocity of her arms is not only tangential. . . but also radial. So the arms are accelerated inward, and the force required times the Δr does the work to raise the kinetic energy

Conservation of Angular Momentum Angular momentum is also conserved in rotational collisions larger I, same total angular momentum, smaller angular velocity

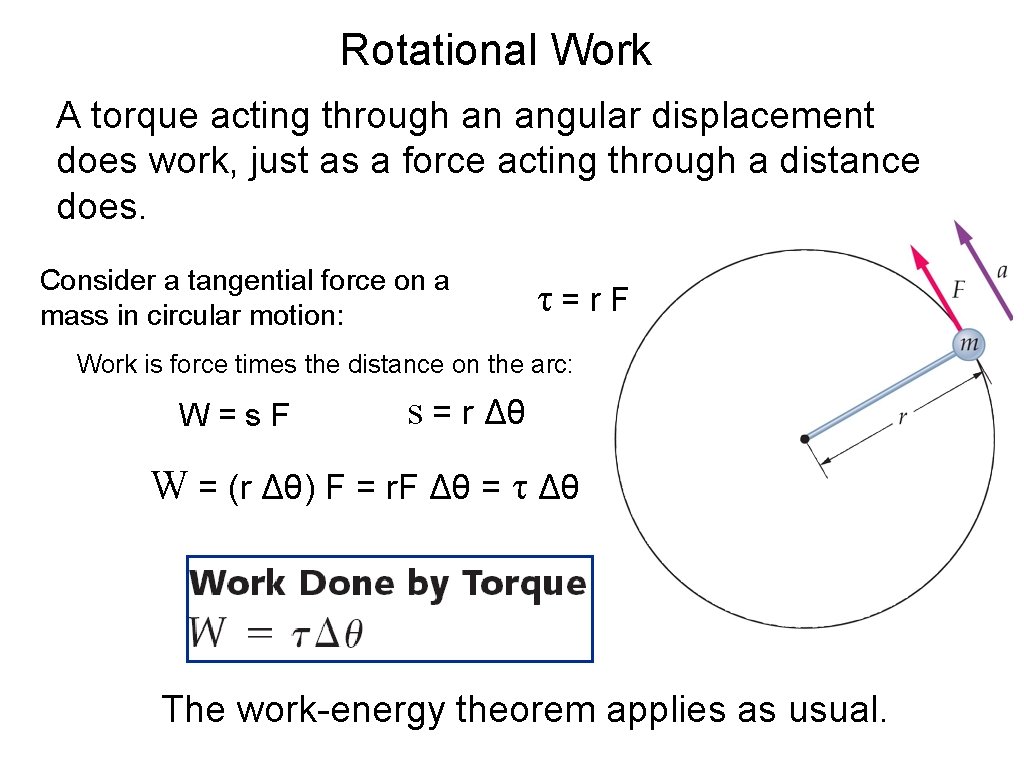
Rotational Work A torque acting through an angular displacement does work, just as a force acting through a distance does. Consider a tangential force on a mass in circular motion: τ=r. F Work is force times the distance on the arc: W=s. F s = r Δθ W = (r Δθ) F = r. F Δθ = τ Δθ The work-energy theorem applies as usual.

Rotational Work and Power is the rate at which work is done, for rotational motion as well as for translational motion. Again, note the analogy to the linear form (for constant force along motion):

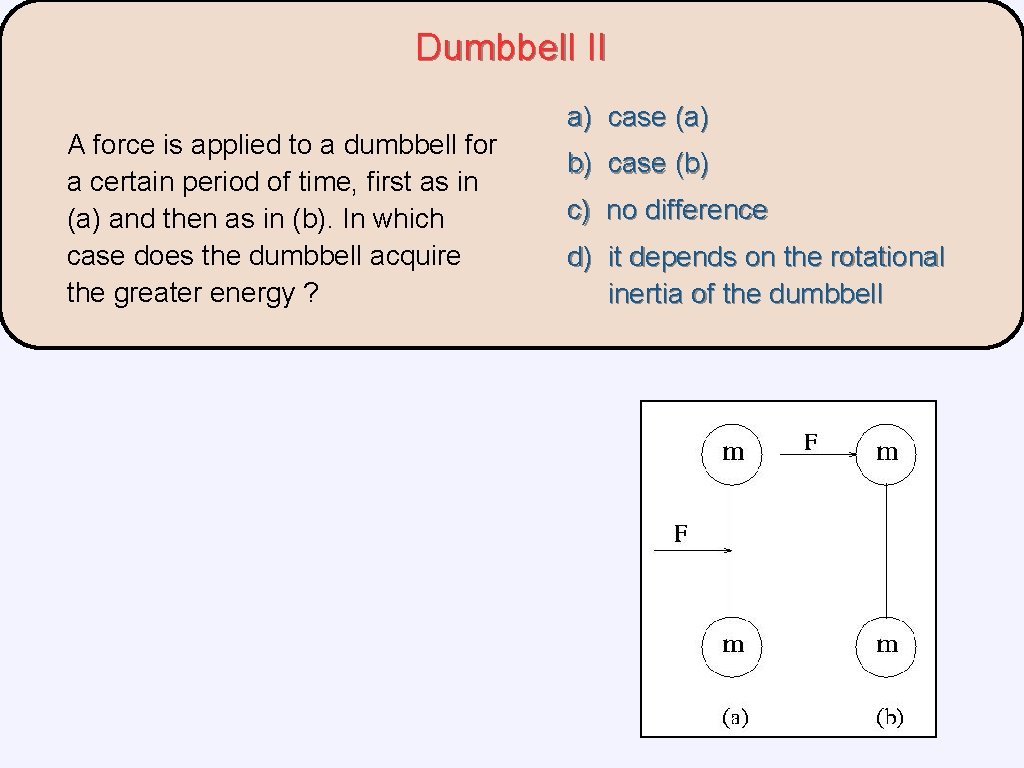
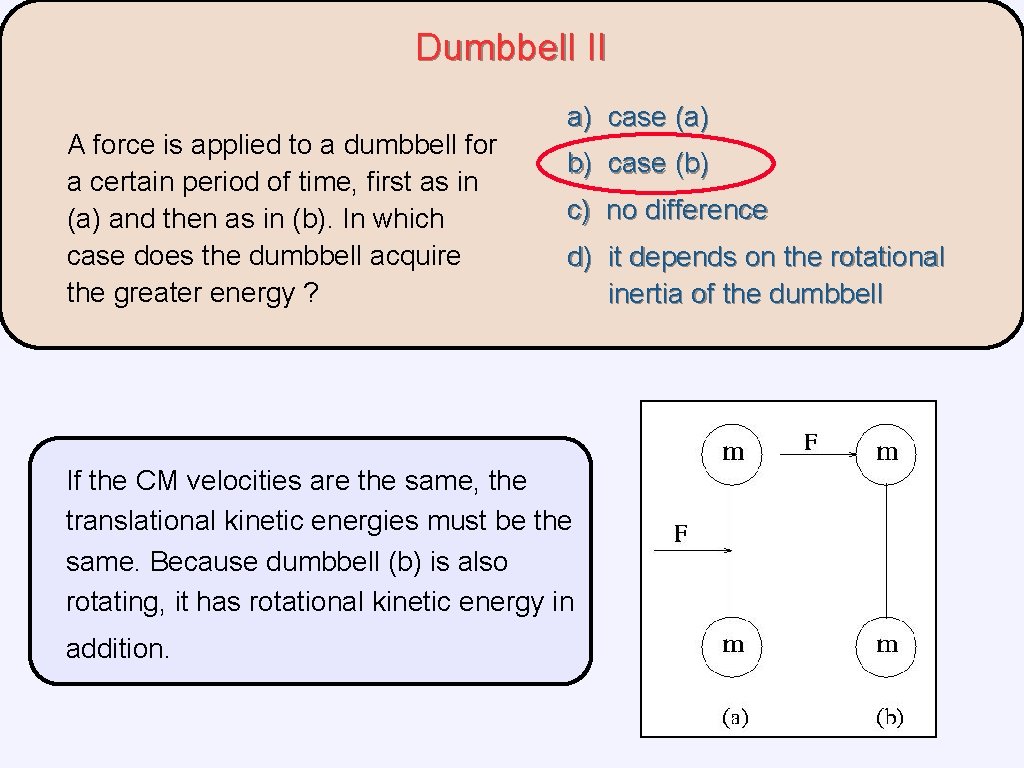
Dumbbell II A force is applied to a dumbbell for a certain period of time, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater energy ? a) case (a) b) case (b) c) no difference d) it depends on the rotational inertia of the dumbbell

Dumbbell II A force is applied to a dumbbell for a certain period of time, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater energy ? a) case (a) b) case (b) c) no difference d) it depends on the rotational inertia of the dumbbell If the CM velocities are the same, the translational kinetic energies must be the same. Because dumbbell (b) is also rotating, it has rotational kinetic energy in addition.

A 2. 85 -kg bucket is attached to a disk-shaped pulley of radius 0. 121 m and mass 0. 742 kg. If the bucket is allowed to fall, (a) what is its linear acceleration? (b) What is the angular acceleration of the pulley? (c) How far does the bucket drop in 1. 50 s?

A 2. 85 -kg bucket is attached to a disk-shaped pulley of radius 0. 121 m and mass 0. 742 kg. If the bucket is allowed to fall, (a) What is its linear acceleration? (b) What is the angular acceleration of the pulley? (c) How far does the bucket drop in 1. 50 s? (a) Pulley spins as bucket falls (b) (c)

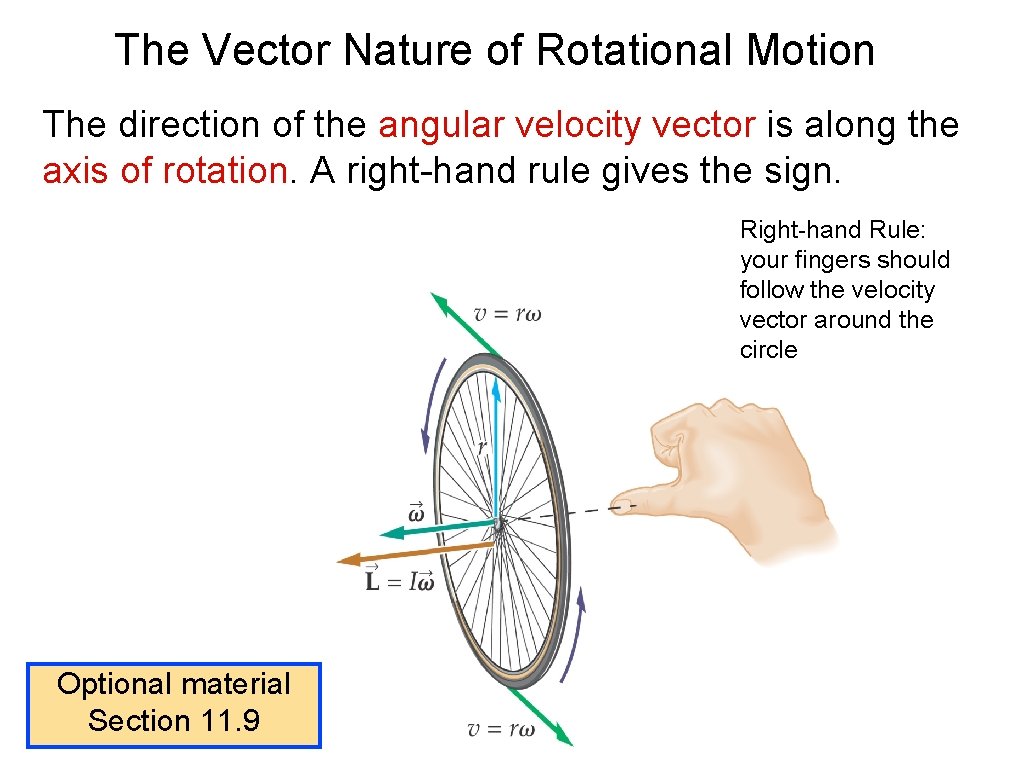
The Vector Nature of Rotational Motion The direction of the angular velocity vector is along the axis of rotation. A right-hand rule gives the sign. Right-hand Rule: your fingers should follow the velocity vector around the circle Optional material Section 11. 9

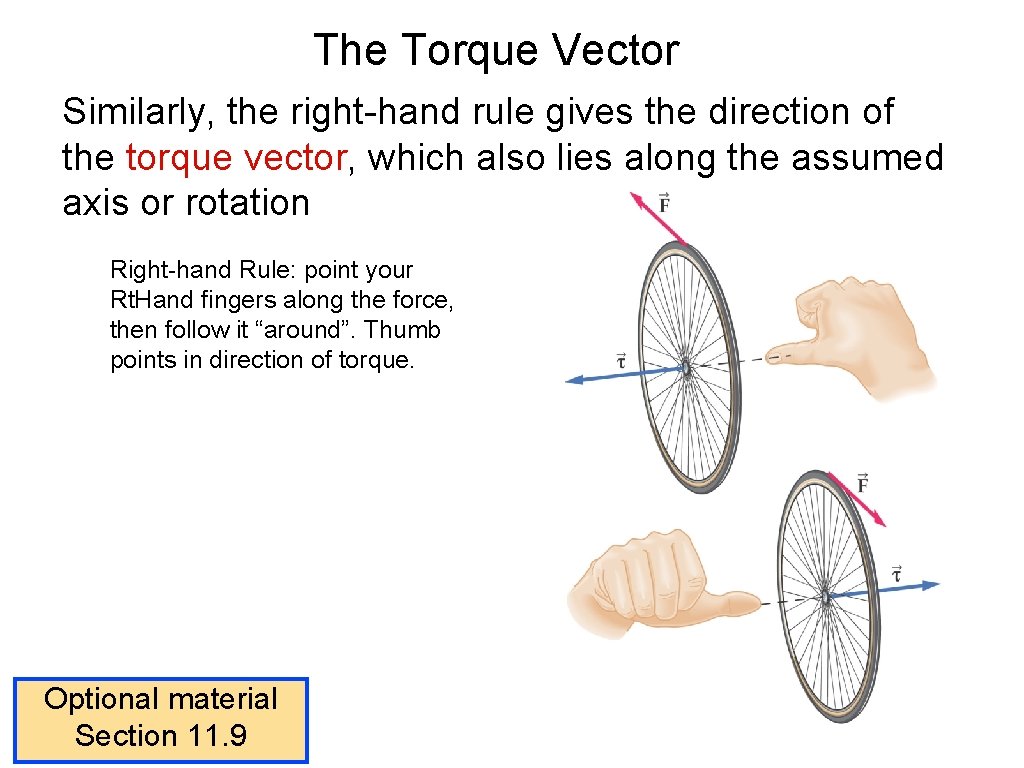
The Torque Vector Similarly, the right-hand rule gives the direction of the torque vector, which also lies along the assumed axis or rotation Right-hand Rule: point your Rt. Hand fingers along the force, then follow it “around”. Thumb points in direction of torque. Optional material Section 11. 9

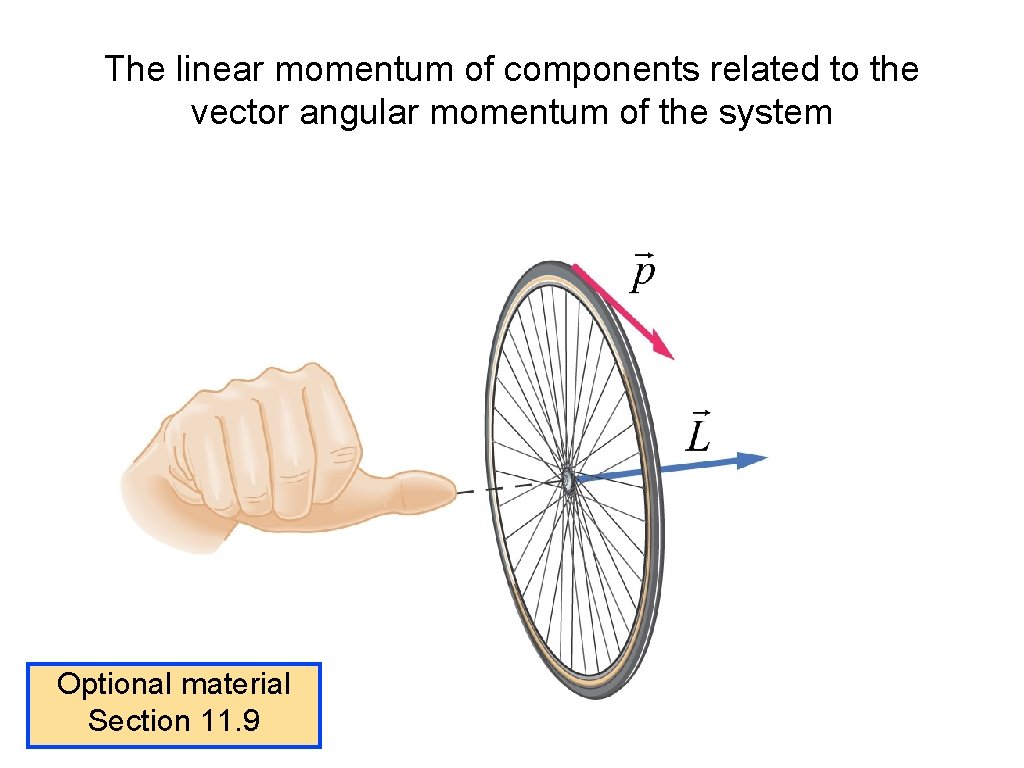
The linear momentum of components related to the vector angular momentum of the system Optional material Section 11. 9

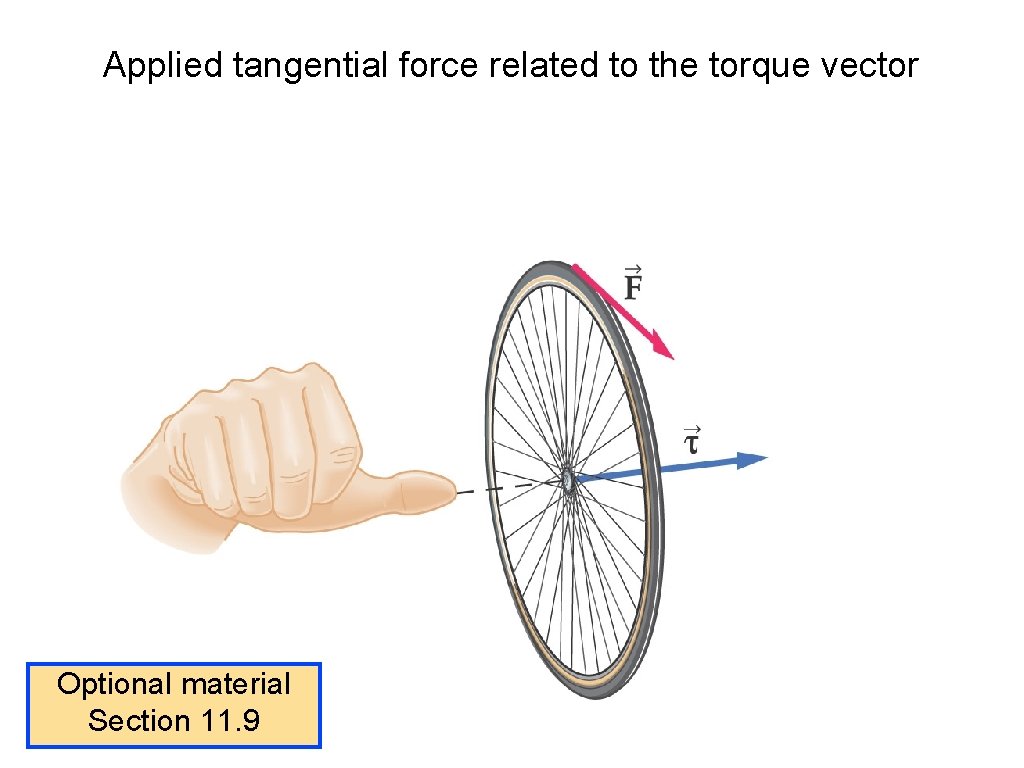
Applied tangential force related to the torque vector Optional material Section 11. 9

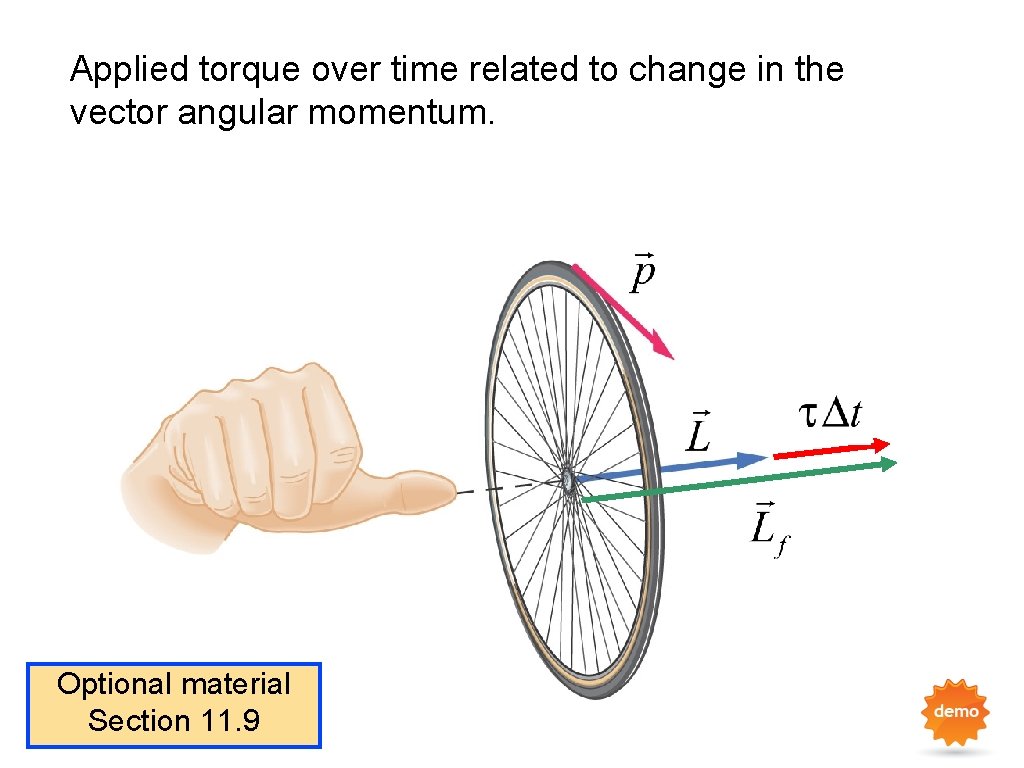
Applied torque over time related to change in the vector angular momentum. Optional material Section 11. 9

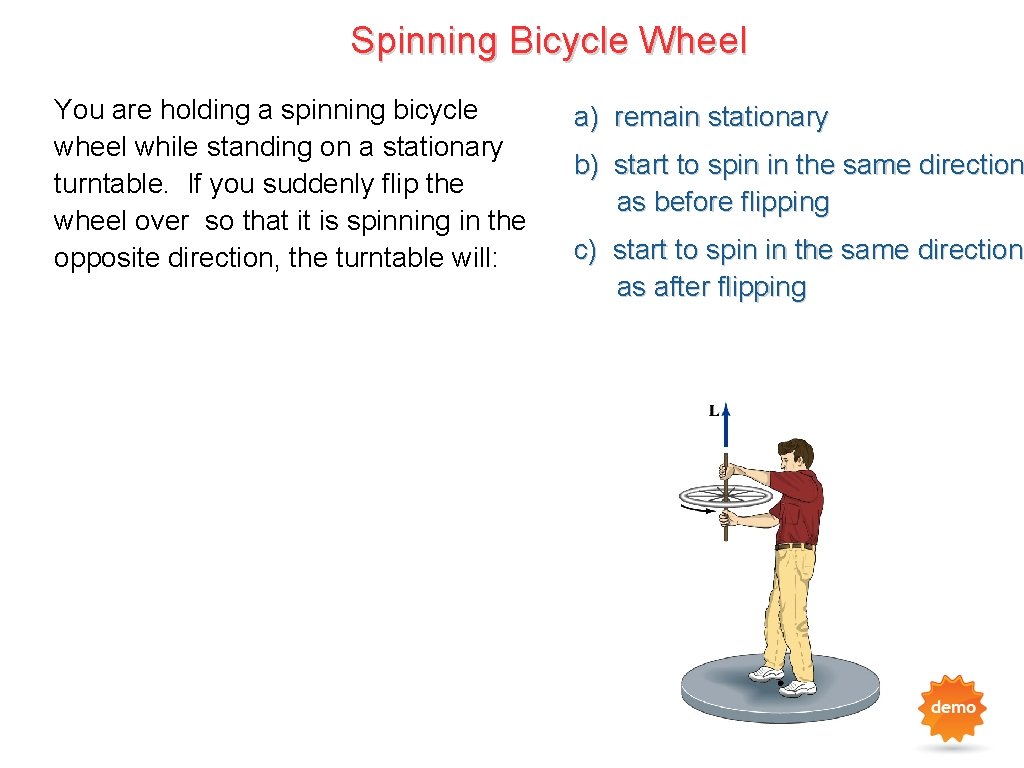
Spinning Bicycle Wheel You are holding a spinning bicycle wheel while standing on a stationary turntable. If you suddenly flip the wheel over so that it is spinning in the opposite direction, the turntable will: a) remain stationary b) start to spin in the same direction as before flipping c) start to spin in the same direction as after flipping

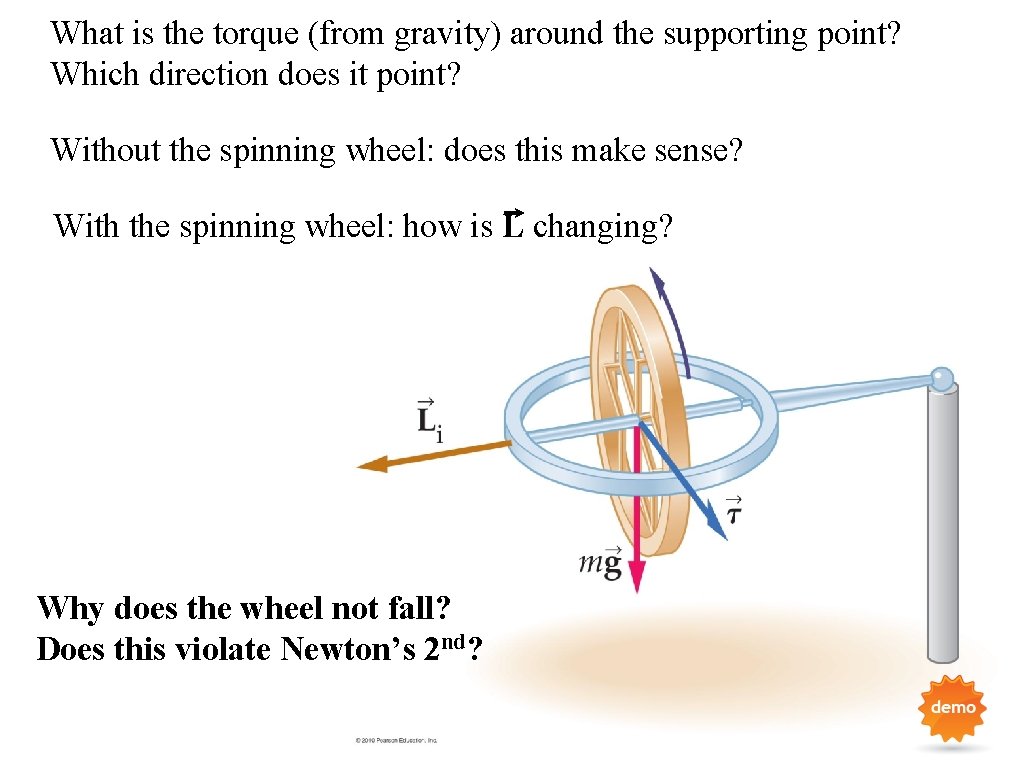
What is the torque (from gravity) around the supporting point? Which direction does it point? Without the spinning wheel: does this make sense? With the spinning wheel: how is L changing? Why does the wheel not fall? Does this violate Newton’s 2 nd?