Leccin 17 Indice 17 1 Introduccin al Potencial

Lección 17 : Indice • 17. 1. - Introducción al Potencial Interno. • 17. 3. - Teorema de Clapeyron. Expresiones del potencial interno. • 17. 4. - Teorema de reciprocidad de Maxwell - Betti.

Lección 18 : Indice • 18. 1. - Teorema de Castigliano. Integrales de Mohr. • 18. 2. - Teorema inverso de Castigliano. • 18. 3. - Sistemas hiperestáticos exteriormente. Teorema de Menabrea o de la energía mínima. • 18. 4. - Sistemas hiperestáticos interiormente. • 18. 5. - Entramados de barras articuladas.

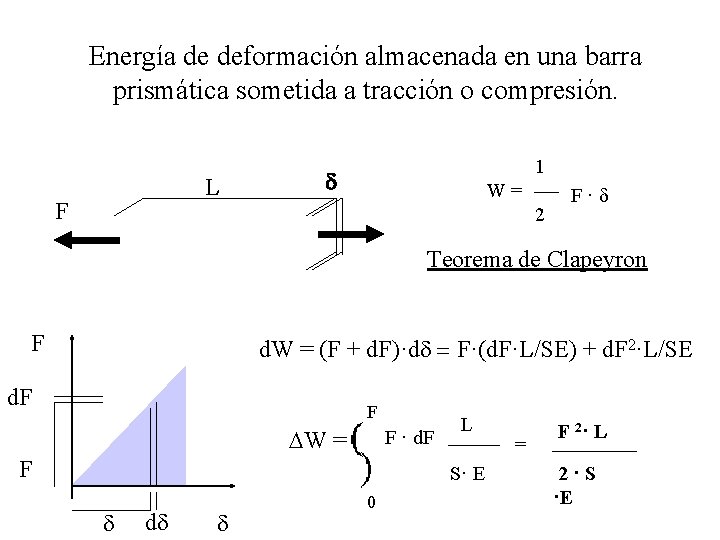
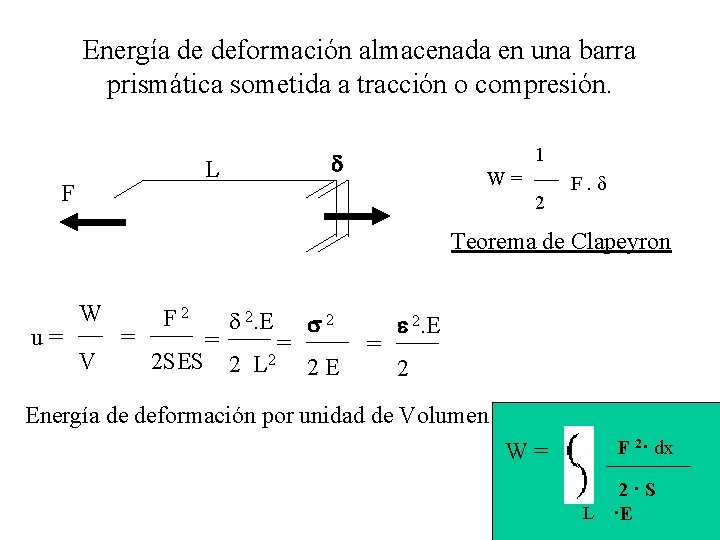
Energía de deformación almacenada en una barra prismática sometida a tracción o compresión. L F 1 d W= 2 F·d Teorema de Clapeyron F d. W = (F + d. F)·dd = F·(d. F·L/SE) + d. F 2·L/SE d. F F DW = F · d. F F L S· E d dd d 0 = F 2· L 2·S ·E

Energía de deformación almacenada en una barra prismática sometida a tracción o compresión. L F 1 d W= 2 F. d Teorema de Clapeyron u= W V = F 2 2 SES = d 2. E 2 L 2 = s 2 2 E = e 2. E 2 Energía de deformación por unidad de Volumen W= F 2· dx 2·S L ·E

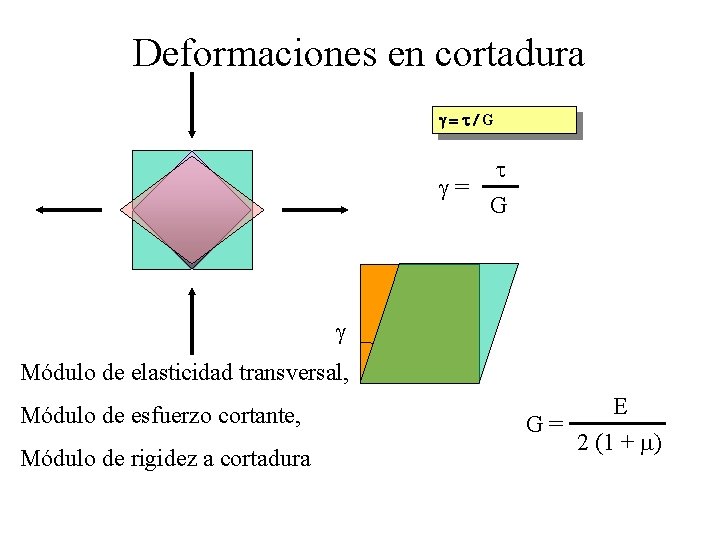
Deformaciones en cortadura g=t/G t g= G g Módulo de elasticidad transversal, Módulo de esfuerzo cortante, Módulo de rigidez a cortadura E G= 2 (1 + m)

Energía de deformación en cortadura por unidad de Volumen Energía de deformación en tracción por unidad de Volumen W= 1 2 F·d u= d 2 · E s 2 = 2 2 E Energía de deformación en cortadura por unidad de Volumen u= g 2 · G t 2 = 2 2 G

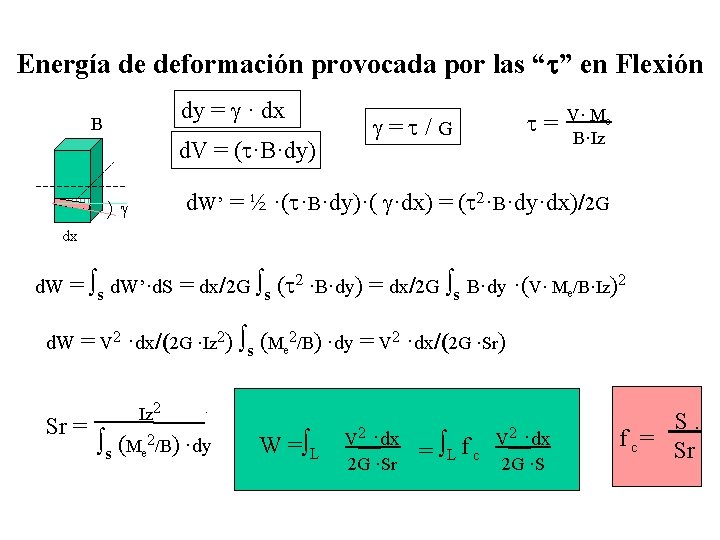
Energía de deformación provocada por las “t” en Flexión dy = g · dx B t= g=t/G d. V = (t·B·dy) V· Me B·Iz d. W’ = ½ ·(t·B·dy)·( g·dx) = (t 2·B·dy·dx)/2 G g dx d. W = s d. W’·d. S = dx/2 G s (t 2 ·B·dy) = dx/2 G s B·dy ·(V· Me/B·Iz)2 d. W = V 2 ·dx/(2 G ·Iz 2) s (Me 2/B) ·dy = V 2 ·dx/(2 G ·Sr) Sr = Iz 2 . s (Me 2/B) ·dy W = L V 2 ·dx 2 G ·Sr = L f c V 2 ·dx 2 G ·S S. f c = Sr

Energía de deformación en Flexión W= 1 2 F·d u= d 2 · E s 2 = 2 2 E Energía de deformación en Flexión s= M·y Iz V= d. S·dx d. W= u·V = M 2·dx/2 EIz W= L M 2·dx 2 EIz

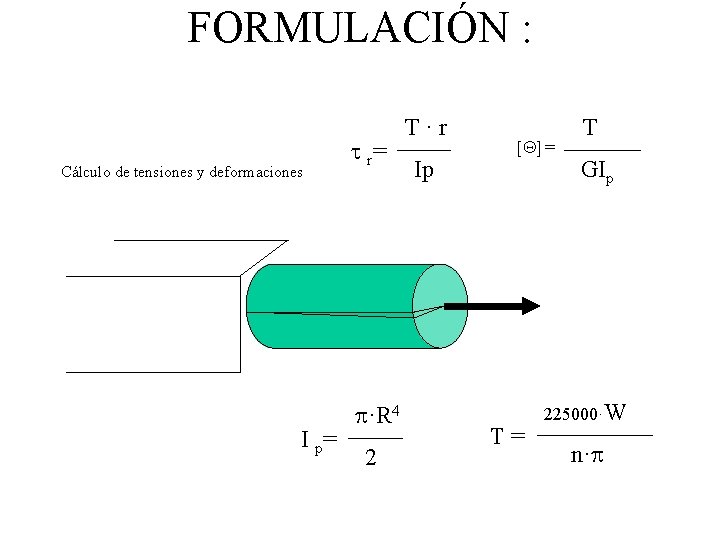
FORMULACIÓN : Cálculo de tensiones y deformaciones I p= t r= p·R 4 2 T·r Ip [Q] = T= T GIp 225000·W n·p

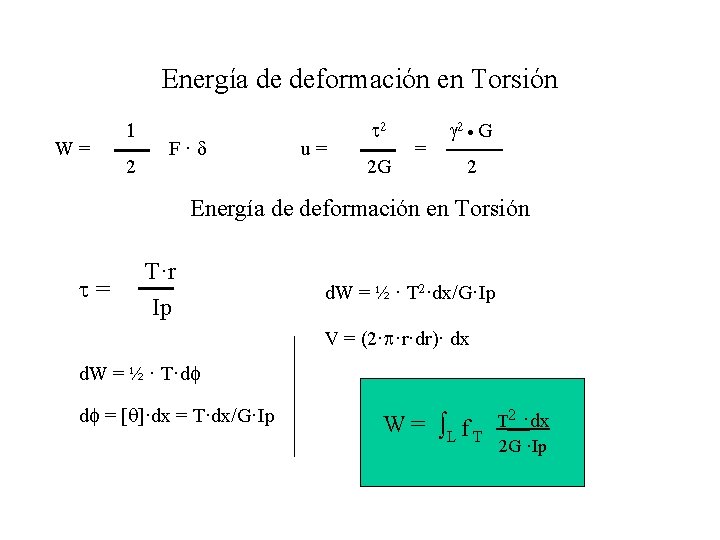
Energía de deformación en Torsión W= 1 2 F·d u= t 2 2 G = g 2 · G 2 Energía de deformación en Torsión t= T·r Ip d. W = ½ · T 2·dx/G·Ip V = (2·p·r·dr)· dx d. W = ½ · T·df df = [q]·dx = T·dx/G·Ip W = L f T T 2 ·dx 2 G ·Ip

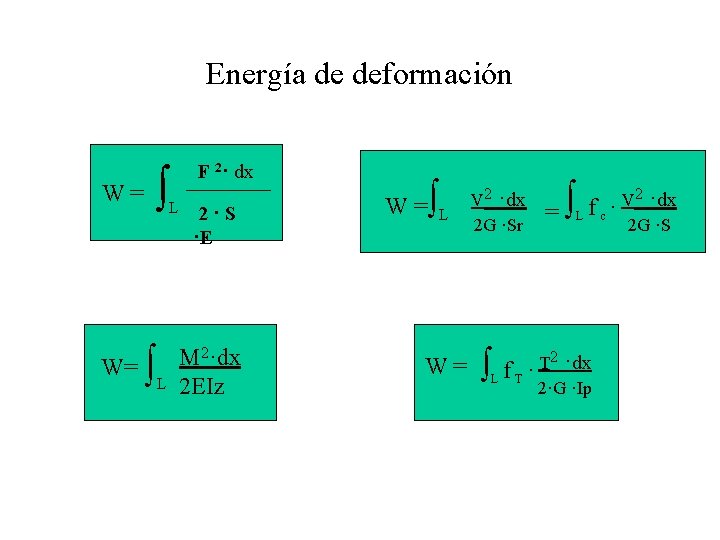
Energía de deformación W= W= L F 2· dx L 2·S ·E M 2·dx 2 EIz W= L W= V 2 ·dx 2 G ·Sr = V 2 ·dx Lfc· 2 G ·S 2 ·dx T Lf. T· 2·G ·Ip

Expresiones de potencial interno • Módulo de Resiliencia: – Máxima energía de deformación, por unidad de volumen que se puede almacenar en un cuerpo sin que se produzcan deformaciones permanentes. d. W = ½ · [s. T]·[e] UTotal = UN + UV + UMF + UMT U= F 2· dx L 2·S ·E + V 2 ·dx Lfc· 2·G ·S + L M 2·dx 2·E·Iz + T 2 ·dx Lf. T· 2·G ·Ip

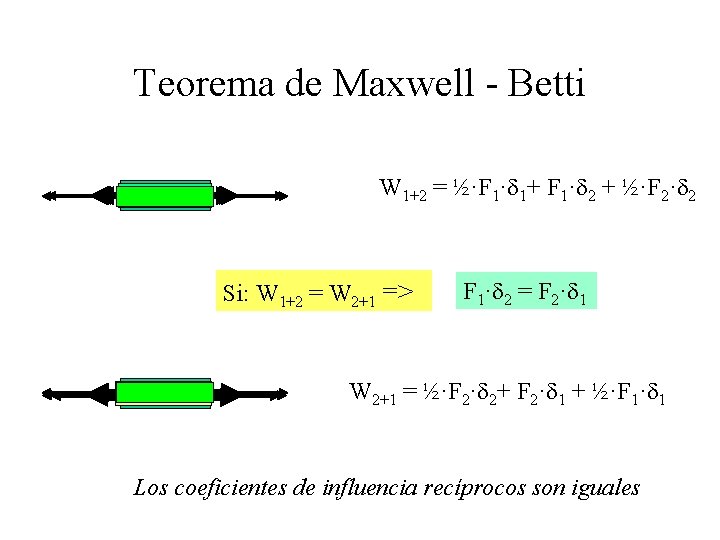
Teorema de Maxwell - Betti W 1+2 = ½·F 1·d 1+ F 1·d 2 + ½·F 2·d 2 Si: W 1+2 = W 2+1 => F 1·d 2 = F 2·d 1 W 2+1 = ½·F 2·d 2+ F 2·d 1 + ½·F 1·d 1 Los coeficientes de influencia recíprocos son iguales

Teorema de Castigliano La derivada parcial del potencial interno de un sistema elástico, sometido a un conjunto de acciones, respecto a una de ellas es igual a la proyección, sobre la dirección y sentido de la acción, del correspondiente desplazamiento de su punto de aplicación originado por el conjunto de todas ellas. U= F 2· dx L 2·S ·E + V 2 ·dx L f c· 2·G ·S + L M 2·dx 2·E·Iz + T 2 ·dx L f T· 2·G ·Ip d. F = ∂U/∂F = ∫(∂MF 2 /∂F) ·dx/(2·E·Iz) = ∫ MF ·(∂MF/∂F) ·dx/(E·Iz) FM =∂U/∂M = ∫(∂MF 2 /∂M) ·dx/(2·E·Iz) = ∫MF ·(∂MF/∂M) ·dx/(E·Iz)

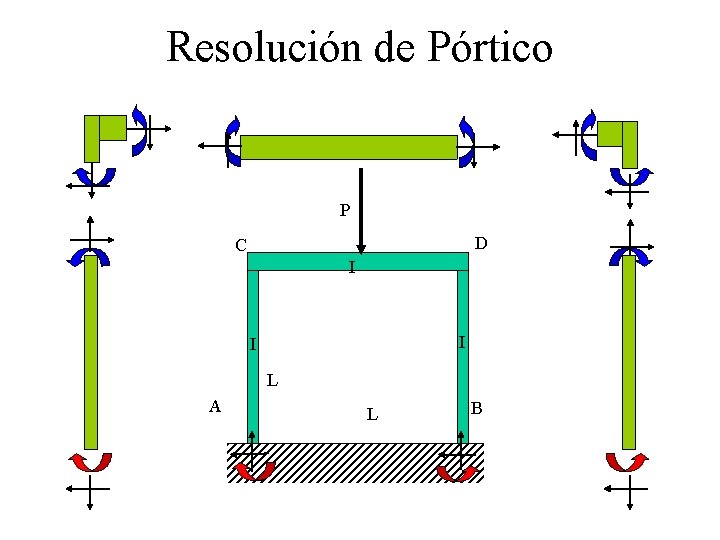
Resolución de Pórtico P D C I I I L A L B

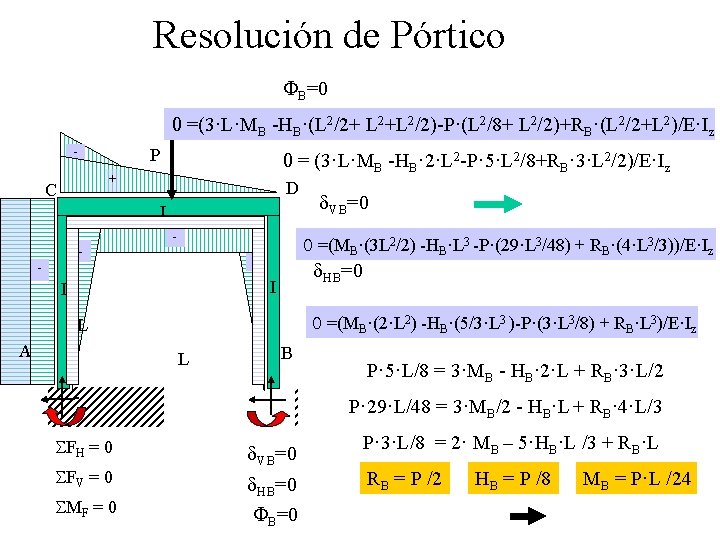
Resolución de Pórtico FB=0 0 =(3·L·MB -HB·(L 2/2+ L 2+L 2/2)-P·(L 2/8+ L 2/2)+RB·(L 2/2+L 2)/E·Iz P 0 = (3·L·MB -HB· 2·L 2 -P· 5·L 2/8+RB· 3·L 2/2)/E·Iz + C D I - - 0 =(MB·(3 L 2/2) -HB·L 3 -P·(29·L 3/48) + RB·(4·L 3/3))/E·Iz - d. HB=0 - I I 0 =(MB·(2·L 2) -HB·(5/3·L 3 )-P·(3·L 3/8) + RB·L 3)/E·Iz L A d. VB=0 L B P· 5·L/8 = 3·MB - HB· 2·L + RB· 3·L/2 P· 29·L/48 = 3·MB/2 - HB·L + RB· 4·L/3 SFH = 0 SFV = 0 SMF = 0 d. VB=0 d. HB=0 FB=0 P· 3·L/8 = 2· MB – 5·HB·L /3 + RB·L RB = P /2 HB = P /8 MB = P·L /24

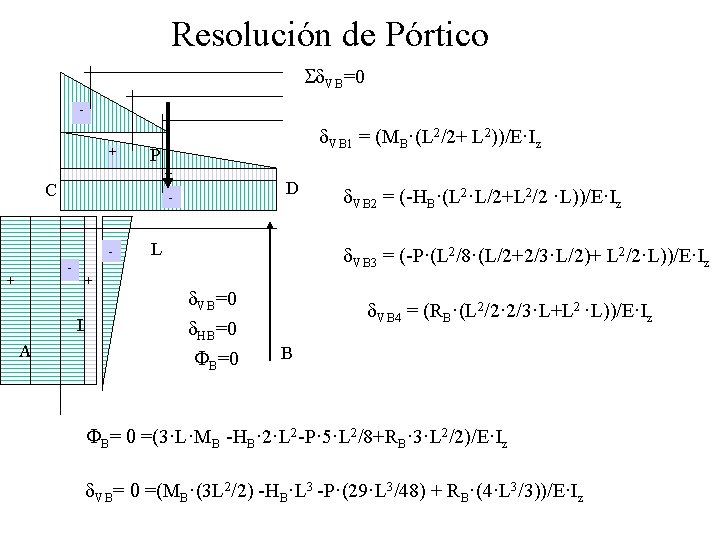
Resolución de Pórtico Sd. VB=0 + P + C + - L A D - + d. VB 1 = (MB·(L 2/2+ L 2))/E·Iz L d. VB 2 = (-HB·(L 2·L/2+L 2/2 ·L))/E·Iz d. VB 3 = (-P·(L 2/8·(L/2+2/3·L/2)+ L 2/2·L))/E·Iz d. VB=0 d. HB=0 FB=0 d. VB 4 = (RB·(L 2/2· 2/3·L+L 2 ·L))/E·Iz B FB= 0 =(3·L·MB -HB· 2·L 2 -P· 5·L 2/8+RB· 3·L 2/2)/E·Iz d. VB= 0 =(MB·(3 L 2/2) -HB·L 3 -P·(29·L 3/48) + RB·(4·L 3/3))/E·Iz

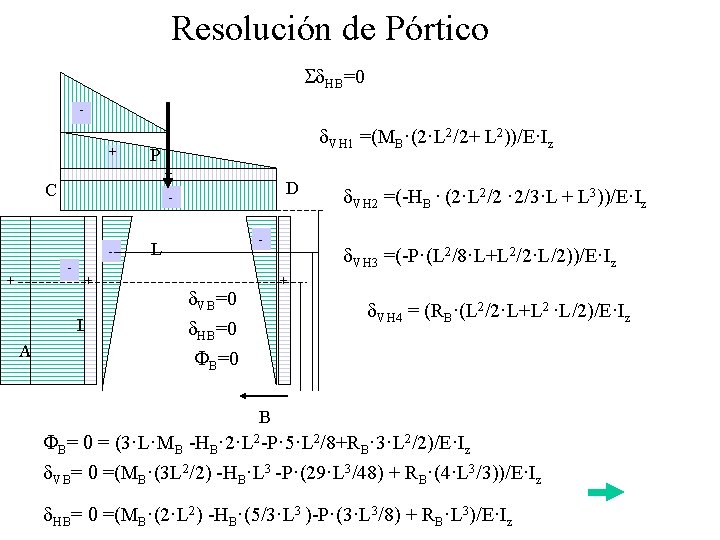
Resolución de Pórtico Sd. HB=0 + P + C + - L A D - + d. VH 1 =(MB·(2·L 2/2+ L 2))/E·Iz - L d. VH 2 =(-HB · (2·L 2/2 · 2/3·L + L 3))/E·Iz d. VH 3 =(-P·(L 2/8·L+L 2/2·L/2))/E·Iz + d. VB=0 d. VH 4 = (RB·(L 2/2·L+L 2 ·L/2)/E·Iz d. HB=0 FB=0 B FB= 0 = (3·L·MB -HB· 2·L 2 -P· 5·L 2/8+RB· 3·L 2/2)/E·Iz d. VB= 0 =(MB·(3 L 2/2) -HB·L 3 -P·(29·L 3/48) + RB·(4·L 3/3))/E·Iz d. HB= 0 =(MB·(2·L 2) -HB·(5/3·L 3 )-P·(3·L 3/8) + RB·L 3)/E·Iz

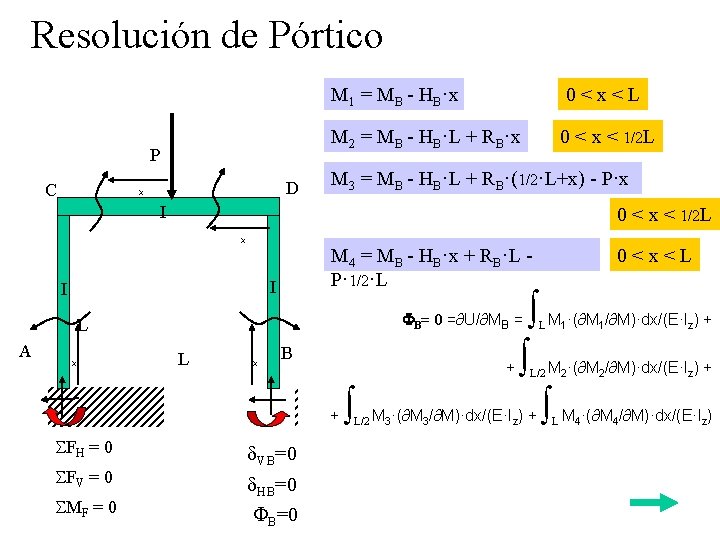
Resolución de Pórtico P C D x M 1 = MB - HB·x 0<x<L M 2 = MB - HB·L + RB·x 0 < x < 1/2 L M 3 = MB - HB·L + RB·(1/2·L+x) - P·x I 0 < x < 1/2 L x M 4 = MB - HB·x + RB·L P· 1/2·L I I A x L x B + + SFH = 0 SFV = 0 SMF = 0 FB= 0 =∂U/∂MB = L d. VB=0 d. HB=0 FB=0 L/2 M 3·(∂M 3/∂M)·dx/(E·Iz) 0<x<L L M 1·(∂M 1/∂M)·dx/(E·Iz) + L/2 M 2·(∂M 2/∂M)·dx/(E·Iz) + + L M 4·(∂M 4/∂M)·dx/(E·Iz)

Resolución de Pórtico M 2 = MB - HB·L + RB·x 0<x<L M 1 = MB - HB·x M 3 = MB - HB·L + RB·(1/2·L+x) - P·x 0 < x < 1/2 L M 4 = MB - HB·x + RB·L - P· 1/2·L 0<x<L (∂M 1/∂RB)= 0 ; (∂M 2/∂HB)= x ; (∂M 3/∂HB)= ½·L+x ; (∂M 4/∂MB)= L d. BR=0 =∂U/∂RB = = + = L M 1·(∂M 1/∂ RB)/(E·Iz) + L/2 M 2·(∂M 2/∂ MB - HB·x) ·(0)/(E·Iz) + P·x)·(1/2·L+x) L( L( = L/2 ( RB)/(E·Iz) + ( B 2+ RB· 1/3·x 3) /(E·Iz) ¼·RB·L·x 2 – ¼·P· L·x 2)/(E·Iz) L· 1/3·x 3)/(E·Iz) ) ] L/2 + L/2 M 3·(∂M 3/∂ MB - HB·L + RB·x)·(x)/(E·Iz) + MB - HB·x + RB·L - P· 1/2·L)·(L)/(E·Iz) = [ M ·½·x - ½·H ·L·x + ( B L/2 ( ] [M· L/2 + ( 2 B 2+ L M 4·(∂M 4/∂ RB)/(E·Iz) = MB - HB·L + RB·(1/2·L+x) - B 1/2·L·x - ] [ M ·½·x - ½·H ·L·x L/2 RB)/(E·Iz) + ½·HB·L 2 ·x· + ¼·RB·L 2·x + RB·¼·L·x 2 + RB 1/3·x 3) - P·

Resolución de Pórtico P· 5·L/8 = 3·MB - HB· 2·L + RB· 3·L/2 P· 29·L/48 = 3·MB/2 - HB·L + RB· 4·L/3 P· 3·L/8 = 2· MB – 5·HB·L /3 + RB·L RB = P /2 HB = P /8 3·M – 2·H·L + 3/2·R·L - 5/8·P·L = 0 -2·M + 5/3·H·L - R·L - 3/8·P·L = 0 3/2·M - H·L + 4/3·R·L - 29/48·P·L = 0 MB = P·L /24