REPASO Potencial Efectivo Potencial centrfugo Ejemplo Potencial elstico

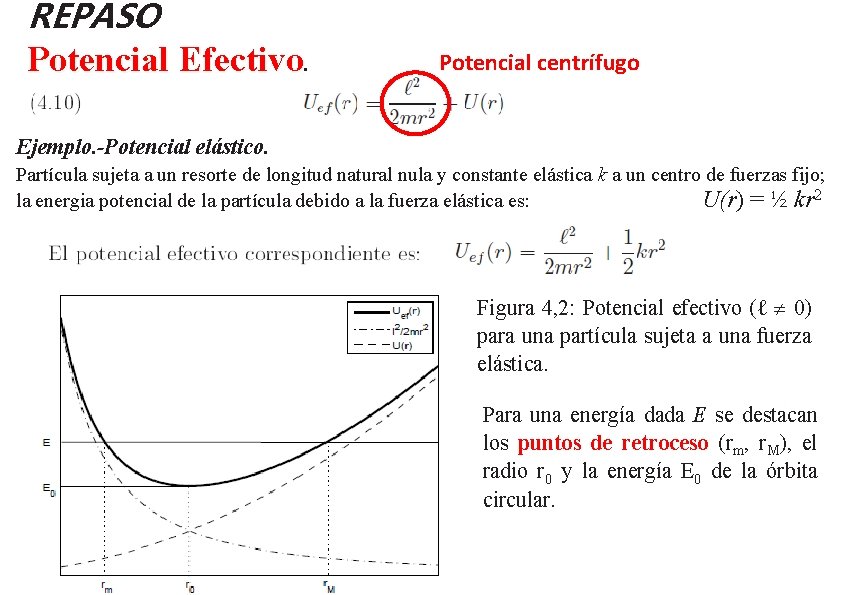
REPASO Potencial Efectivo. Potencial centrífugo Ejemplo. -Potencial elástico. Partícula sujeta a un resorte de longitud natural nula y constante elástica k a un centro de fuerzas fijo; U(r) = ½ kr 2 la energia potencial de la partícula debido a la fuerza elástica es: Figura 4, 2: Potencial efectivo (ℓ 0) para una partícula sujeta a una fuerza elástica. Para una energía dada E se destacan los puntos de retroceso (rm, r. M), el radio r 0 y la energía E 0 de la órbita circular.

4. 2. 2. Leyes horarias. A partir de la expresión (4, 9) para la energía del problema unidimensional. podemos hallar las leves horarias r(t), q(t) como sigue: despejamos r

4. 3. Fórmulas de Binet. Existe una forma alternativa de obtener la trayectoria de un móvil que, para algunos campos centrales, es mucho más efectiva que la descrita en el apartado anterior. Este método se basa en re-escribir las ecuaciones de movimiento en términos de una nueva variable.

Partamos de las ecuaciones de movimiento (4. 4), (4. 5): y consideremos ahora el siguiente cambio de variable:

Lo que es equivalente a escribir: Puede ser de utilidad también conocer la relación entre la velocidad de la partícula v la función u v su derivada. El cuadrado de la velocidad en polares es: En la sección que sigue veremos cómo hallar la trayectoria a partir de estas ecuaciones en un caso sencillo.

4. 4. Movimiento Planetario. Nos planteamos ahora estudiar el movimiento de dos cuerpos sometidos. únicamente a la interacción gravitatoria mutua. Para ello, comenzaremos por ver el problema genérico de dos partículas que interactúan entre sí mediante un potencial U(r) función únicamente de la distancia r que separa a las partículas; este problema se conoce como problema de dos cuerpos. 4. 4. 1. Problema de dos cuerpos. Consideremos la segunda ley de Newton para cada una de las partículas:

Por otro lado definamos la masa reducida m :

y sustituyendo en las ecuaciones de movimiento nos queda (ejercicio: verificar esto) : Si ahora sumamos las ecuaciones de movimiento:

4. 4. 2. Fuerza gravitatoria. Veamos ahora el caso de una fuerza f(r) que depende del inverso del cuadrado de la distancia entre las partículas: que en el caso de la interacción gravitatoria corresponde a K = GMm. La energía potencial asociada a esta fuerza es: donde tomamos el potencial de modo que se anule en el infinito. El potencial efectivo asociado se muestra en la figura:

Existe un valor mínimo para este potencial que corresponde a una órbita circular estable. • Para energías E 0 < E < 0, la partícula tiene dos puntos de retorno y por lo tanto describirá una órbita acotada. • Para energías E > 0 tenemos un solo punto de retorno y por lo tanto nos encontraremos con órbitas no acotadas.

Para ver la forma detallada de las órbitas consideremos ahora las fórmulas de Binet para la partícula de masa reducida:

Ejercicio Mostrar que:

De acuerdo a (4. 20),