Last time we proved theorems Theorem 1 For





![f) B A A B B A x [x B x A] by definition f) B A A B B A x [x B x A] by definition](https://slidetodoc.com/presentation_image_h2/8074674817ef1bf6c36d41e727c4ba70/image-8.jpg)

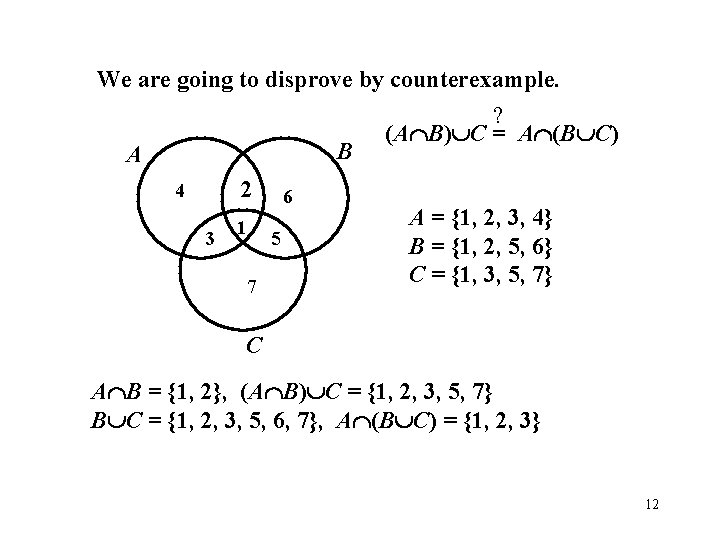










- Slides: 27

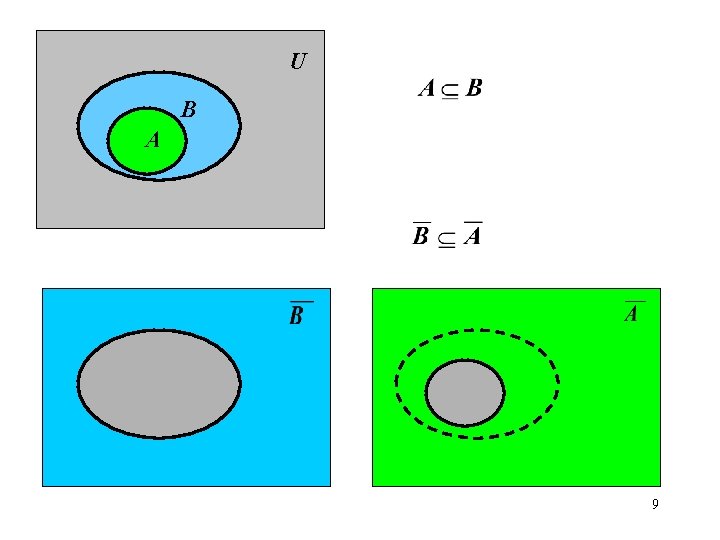
Last time we proved theorems: Theorem 1. For any two sets A and B A A B. Theorem 2. For any two sets A and B A B A. Theorem 3. Let A, B and C be any sets. Then if A B and B C , then A C. 1

We can prove some more theorems by using definitions, logical reasoning and other theorems. Theorem 4. Let A and B be any sets. Then A B if and only if each of the following holds: a) A B=B. A B=B B A B (by Theorem 1) 1. A B=B A B B x A x B 2. A B=B A B x B 2

Proof of A B = B Part 1. A B=B Assume A B. To prove A B=B we need to prove B A B and A B B. B A B by the Theorem 1. To prove A B B take some x A B. Then there might be two cases: either x B or x A implies x B because A B by assumption. So in both cases x B. Thus, for arbitrary x, x A B x B, i. e. A B B. Part 2. A B = B A B Assume A B=B. To prove A B take any x A. By the Theorem 1, x A implies x A B. By assumption A B=B, x A B implies x B. Thus, for arbitrary x A x B, i. e. A B. We proved A B=B and A B=B A B. Thus, it implies that A B=B 3

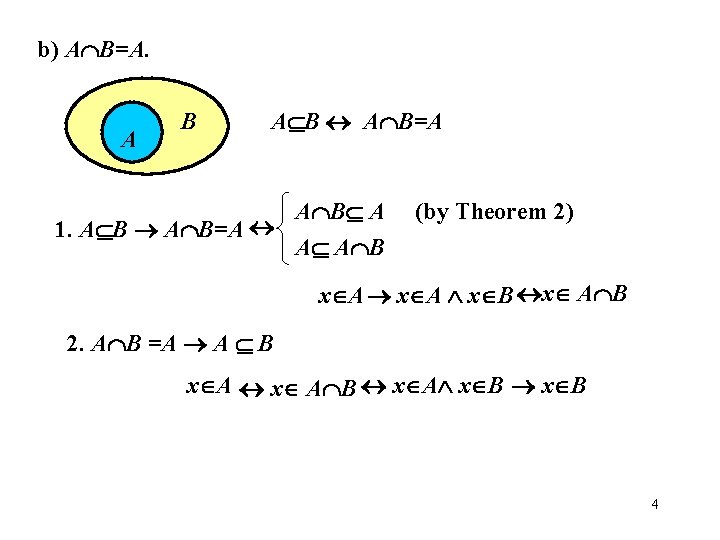
b) A B=A. A B=A A B A 1. A B=A A A B (by Theorem 2) x A x B x A B 2. A B =A A B x A B x A x B 4

Proof of A B=A Part 1. A B=A Assume A B. We need to prove A B A and A A B A by the Theorem 2. To prove A A B take an arbitrary x A. By assumption A B, x A implies that x B, so now we have x A and x B, i. e. x A B by the definition of A B. Part 2. A B=A A B Assume A B=A. To prove A B take some x A. By assumption A B=A, x A implies x A B. By the Theorem 2, x A B implies x B. We proved implications in both directions, A B=A and A B =A A B , that means the propositions are equivalent, A B =A A B 5

c) A B= If you can build the chain of identical (in both directions) transformations, then you don’t need double inclusion. A B x [x A x B] by subset definition by equivalence p q x [x A x B] by De. Morgan’s law x [x A B] by definition of A B x [x A B] by negation of A B = by definition of empty set 6

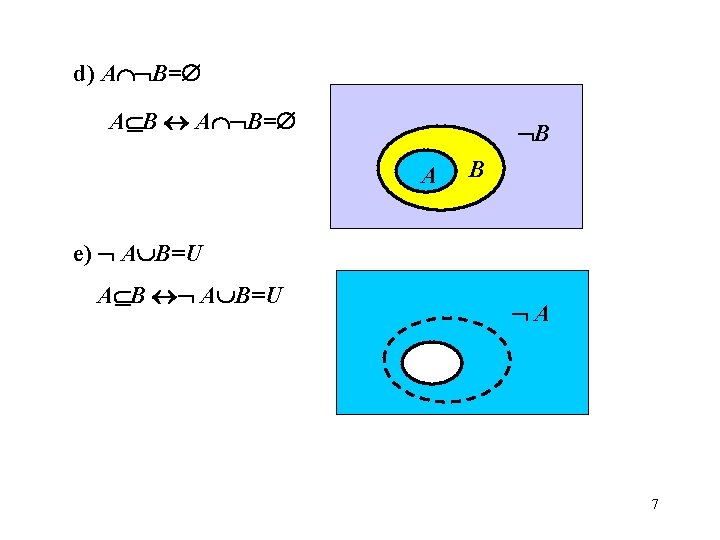
d) A B= A B= B A B e) A B=U A B=U A 7
![f B A A B B A x x B x A by definition f) B A A B B A x [x B x A] by definition](https://slidetodoc.com/presentation_image_h2/8074674817ef1bf6c36d41e727c4ba70/image-8.jpg)
f) B A A B B A x [x B x A] by definition of set compliment x [x A x B] by equivalence of an implication and its contrapositive. A B by definition of subset relation 8

U B A 9

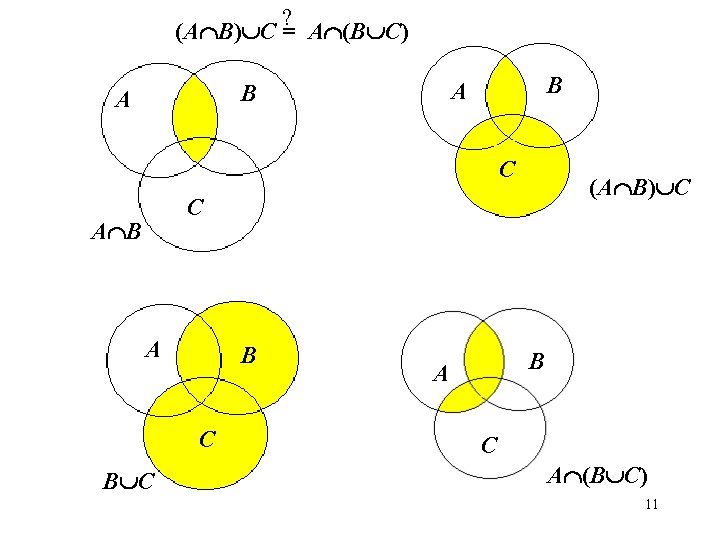
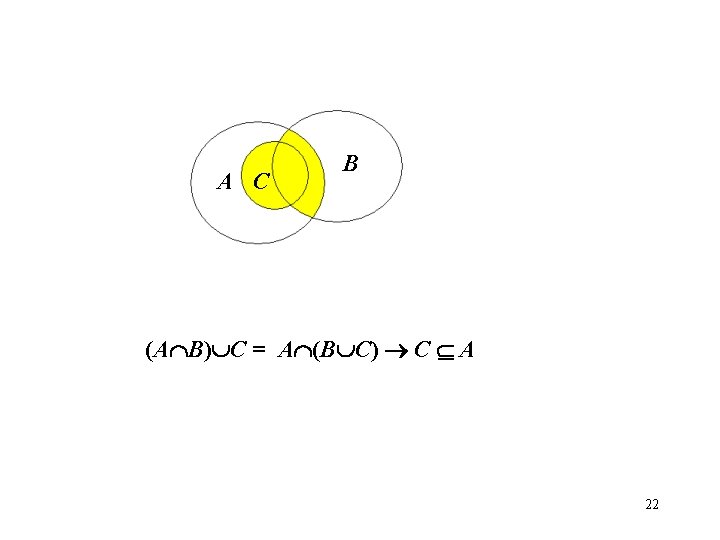
Prove or disprove the following proposition For any three sets A, B and C (A B) C = A (B C) First you need to decide what to do…If the proposition looks like to be true, prove it for arbitrary sets. But suppose you suspect that it not always true… It is sufficient to find a single counterexample to disprove it! To disprove that the proposition is true for any sets its sufficient to find a single example of three sets, such that the proposition is false. 10

? (A B) C = A (B C) B A C (A B) C C A B C B A C A (B C) 11
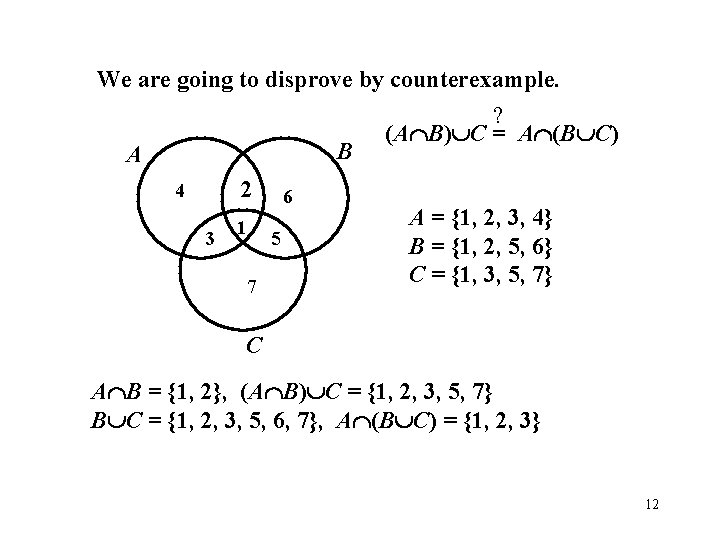
We are going to disprove by counterexample. ? (A B) C = A (B C) B A 2 4 3 1 6 5 7 A = {1, 2, 3, 4} B = {1, 2, 5, 6} C = {1, 3, 5, 7} C A B = {1, 2}, (A B) C = {1, 2, 3, 5, 7} B C = {1, 2, 3, 5, 6, 7}, A (B C) = {1, 2, 3} 12

You can use a membership method here. A B C 1 1 2 1 1 0 3 1 0 1 4 1 0 0 5 0 1 1 6 0 1 0 7 0 0 1 8 0 0 0 A B (A B) C B C A (B C) 1 1 0 0 0 1 1 1 0 1 1 1 0 0 A 4 0 B 2 6 1 3 5 7 C 8 13

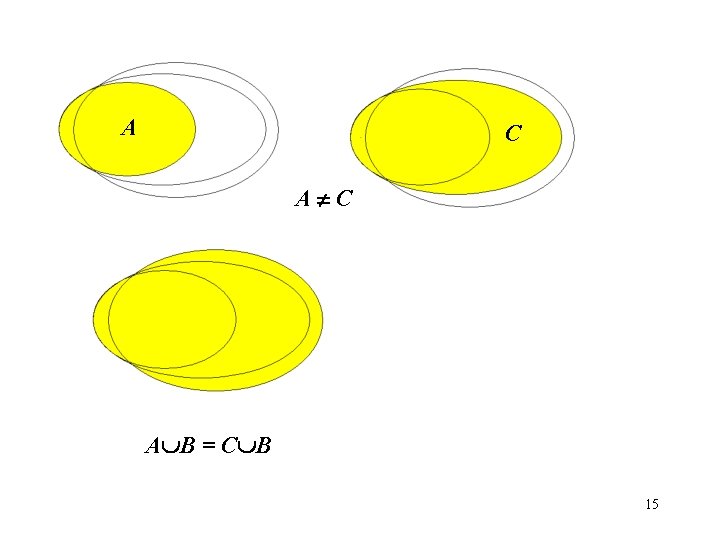
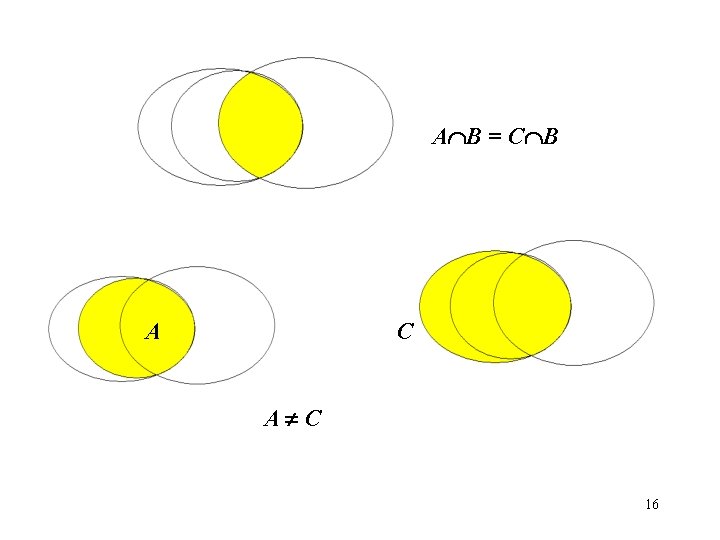
Theorem 5. Let A, B and C be arbitrary sets. Prove that if A B = C B and A B = C B, then A = C. What this theorem says? A B = C B / A=C Counterexample: A = {1}, C ={1, 2}, B ={1, 2} A=C / A B = C B Counterexample: A = {1}, C ={1, 2}, B ={1} But A B = C B and A B = C B A = C 14

A C A B = C B 15

A B = C B A C 16

Theorem 5. Let A, B and C be arbitrary sets. Prove that if A B = C B and A B = C B, then A = C. Direct proof of p q Assume p: A B = C B and A B = C B to prove q: A = C The equality of two sets can be proved as two subset relations (‘double inclusion’ ): A C C A A=C p A C C A p A C p C A So, there should be two parts of the proof. 1). A B = C B and A B = C B A C x A x A B x C B x A B x C 2). A B = C B and A B = C B C A 17

Part 1: proof of A B = C B and A B = C B A C Assume A B = C B (1) and A B = C B (2). To prove A C we need to show that any element from A belongs to C, x [x A x C]. So, take arbitrary element x A (3) to show that x C. By the Theorem 1, (3) implies x A B (4). By assumption (1) we conclude from (4) that x C B (5), or by the definition of the set union that x C or x B (6). So, we have one of two cases to consider. Case x C: we are done. Case x B: we can imply x A B (7) by the Theorem 2. By assumption (2) it can be implied from (7) that x C B (8). From (8) we can conclude that x C making use of the Theorem 2. So, in both cases we come to x C. QED. 18

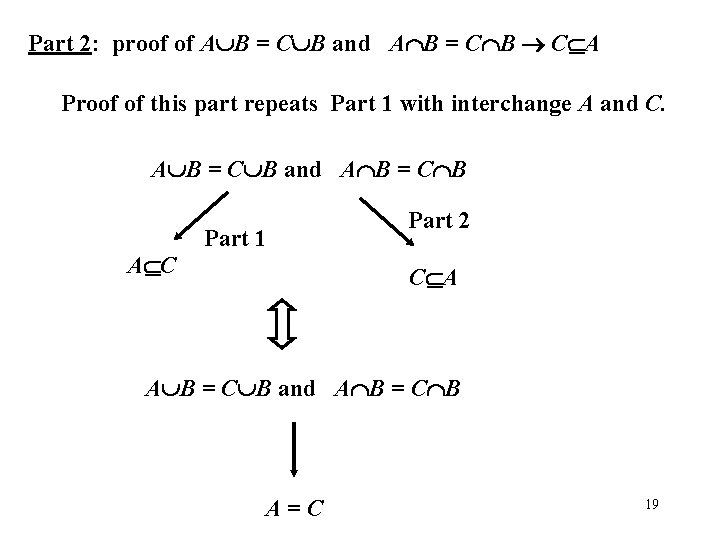
Part 2: proof of A B = C B and A B = C B C A Proof of this part repeats Part 1 with interchange A and C. A B = C B and A B = C B Part 1 A C Part 2 C A A B = C B and A B = C B A=C 19

Consider an example of application of the Theorem 5. Theorem 6. For any three sets A, B and C if (A B) C = A (B C) then C A. Proof. Assume (A B) C = A (B C), (1) to prove C A, (2) (direct proof). (A B) C = (A C) (B C), by distributive law = A (B C), by assumption (1). So we have (A C) (B C)= A (B C), (3). By associative and commutative laws we have: (A C) (B C) = A (B C), (4). By the Theorem 5, (3) and (4) imply that A C =A, (5). By the Theorem 4 a (C A A C =A), (5) implies C A. QED 20

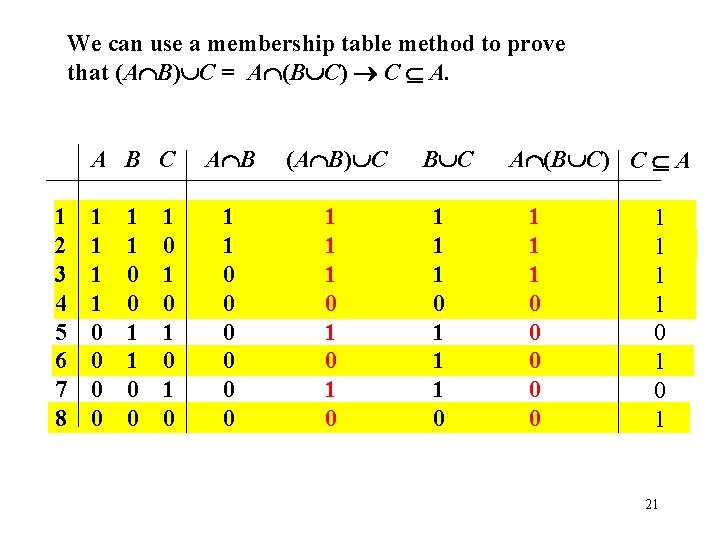
We can use a membership table method to prove that (A B) C = A (B C) C A. A B C 1 1 2 1 1 0 3 1 0 1 4 1 0 0 5 0 1 1 6 0 1 0 7 0 0 1 8 0 0 0 A B (A B) C 1 1 0 0 0 1 1 1 0 1 0 B C 1 1 1 0 A (B C) C A 1 1 1 0 0 0 1 1 0 1 21

A C B (A B) C = A (B C) C A 22

Theorem 7. Suppose A, B and C are sets and A B C. Then A C B. Goal Given A B C A C B x[ x (A C ) x B] Let x be arbitrary x to prove x (A C ) x B A B C x (A C ) x B Try to prove by contradiction 23

Proof by contradiction. Given A B C x (A C ) x B Goal contradiction A B C x A x C x B x A x B x C False 24

Theorem 7. Suppose A, B and C are sets and A B C. Then A C B. Proof. Let x be arbitrary. Suppose x A C. This means x A and x C. Suppose x B. Then x A B and since A B C , x C. But this contradicts to the fact that x C. Therefore x B. Thus, if x A C , then x B. Since x is arbitrary, we can conclude that x [x (A C ) x B], so A C B 25

Theorem 8. Suppose A B, and A and C are disjoint. Prove that A B C. Given A B A C= x A Goal A B C Let x be arbitrary to prove x A x B C x B x C x A x B by A B A C = y [ y A y C ] 26

Theorem 8. Suppose A B, and A and C are disjoint. Prove that A B C. Proof. Let x be arbitrary. Suppose x A. Since A B it follows that x B. Since A and C are disjoint, we must have x C. Thus, x B C. Since x was arbitrary element of A , we can conclude, that A B C. 27
 Green's theorem
Green's theorem Wisdom is proved right by her actions proverbs
Wisdom is proved right by her actions proverbs Who proved copernicus theory
Who proved copernicus theory Facts admitted need not be proved
Facts admitted need not be proved When is a fact said to be proved
When is a fact said to be proved Example of elapsed time
Example of elapsed time Fermat's last theorem
Fermat's last theorem Fermat's last theorem
Fermat's last theorem Last theorem
Last theorem Fspos vägledning för kontinuitetshantering
Fspos vägledning för kontinuitetshantering Novell typiska drag
Novell typiska drag Tack för att ni lyssnade bild
Tack för att ni lyssnade bild Returpilarna
Returpilarna Varför kallas perioden 1918-1939 för mellankrigstiden?
Varför kallas perioden 1918-1939 för mellankrigstiden? En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Adressändring ideell förening
Adressändring ideell förening Tidböcker
Tidböcker Sura för anatom
Sura för anatom Förklara densitet för barn
Förklara densitet för barn Datorkunskap för nybörjare
Datorkunskap för nybörjare Tack för att ni lyssnade bild
Tack för att ni lyssnade bild Hur skriver man en debattartikel
Hur skriver man en debattartikel Autokratiskt ledarskap
Autokratiskt ledarskap Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande Påbyggnader för flakfordon
Påbyggnader för flakfordon Lufttryck formel
Lufttryck formel Publik sektor
Publik sektor Kyssande vind
Kyssande vind