Klargjring fra forrige gang fn Det antall elementre

Klargjøring fra forrige gang f(n): Det antall elementære operasjoner vi kommer fram til i algoritmen g(n): En eller annen referansefunksjon, gjerne n, n 2, nlogn eller liknende O: Verste fall, mest mulig arbeid (for eksempel i if-setninger) Ω: Beste fall, minst mulig arbeid Θ: Både verste og beste kan uttrykkes med samme g

Eksempel: • Har funnet ut at vår algoritme i verste fall utføres 2 n 2+8 n+3 ganger og i beste fall n 2/2 + 5 n + 3 ganger • Verste fall: Siden 2 n 2+8 n+3 <= 4 n 2 når n>=5 har vi f(n)єO(n 2) • Beste fall: Siden n 2/2 + 5 n + 3 >= n 2/2 når n>=0, har vi f(n)єΩ(n 2) • Siden g(n)=n 2 for begge tilfeller, får vi f(n)єΘ(n 2)

Rekursjon Programmeringsteknikk der en metode kaller seg selv

Eksempel: Fakultet n! = n * (n-1)! 5! = 5 * 4! 4! = 4 * 3! 3! = 3 * 2! 2! = 2 * 1! og 1! = 1 2! = 2 * 1 = 2 3! = 3 * 2 = 6 4! = 4 * 6 = 24 5! = 5 * 24 = 120

Oppbygging • En basis – enkelt tilfelle som kan beregnes/utføres direkte (1! = 1) • Et rekursjonstrinn der problemet splittes i et eller flere ny(e) problem(er) av samme type, men enklere enn det opprinnelige (n! = n * (n-1)! ) • Enklere betyr i denne sammenhengen nærmere basis (n-1 er nærmere 1 enn n er)

Tenkemåte • Anta at vi har løst problemet for de(t) enklere problemet/ene. Ikke tenk på hvordan dette skal løses! • Bruk løsningen til å løse det opprinnelige problemet. • Husk å sette opp løsningen for basis. • Se algoritme 2. 1 side 23

Alternativ: iterasjon • Rekursjon krever mye ressurser under kjøring • Hvis det er like enkelt å lage ei løkke, ikke bruk rekursjon! • Rekursjon brukes når det er mye mer komplisert å programmere ikke-rekursivt

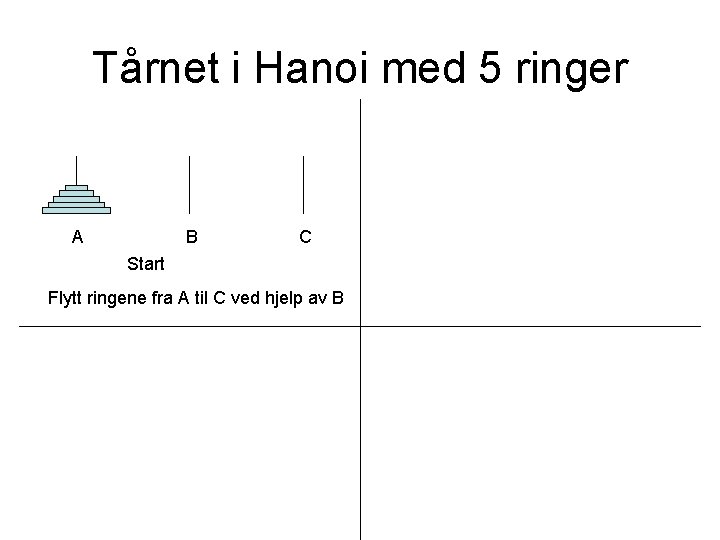
Et eksempel der rekursjon er beste løsning: Tårnet i Hanoi • Har n ringer som skal flyttes fra en pinne til en annen. Har en tredje pinne som kan brukes til mellomlagring underveis • Alle ringene har forskjellig størrelse. Ingen ring får ligge over en mindre ring • Bare en ring får flyttes om gangen

Tårnet i Hanoi med 5 ringer B A C Start Flytt ringene fra A til C ved hjelp av B

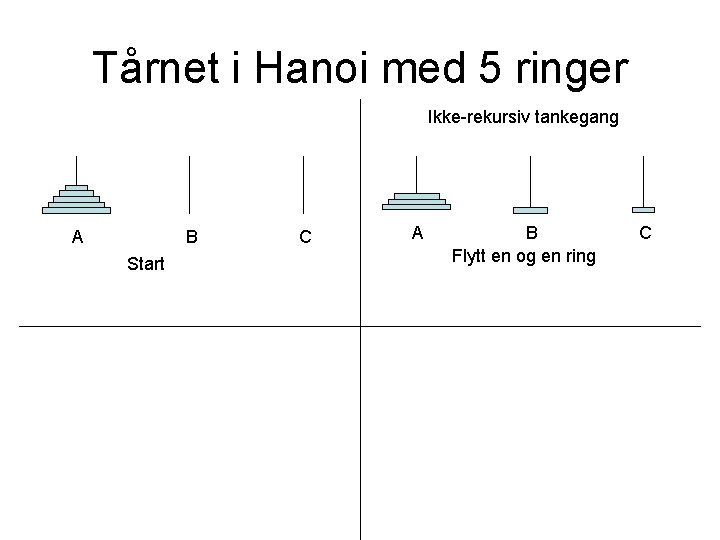
Tårnet i Hanoi med 5 ringer Ikke-rekursiv tankegang B A Start C A B Flytt en og en ring C

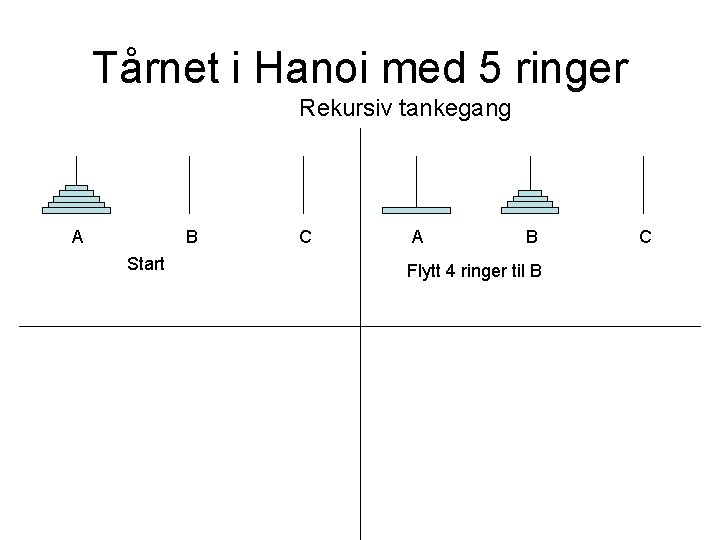
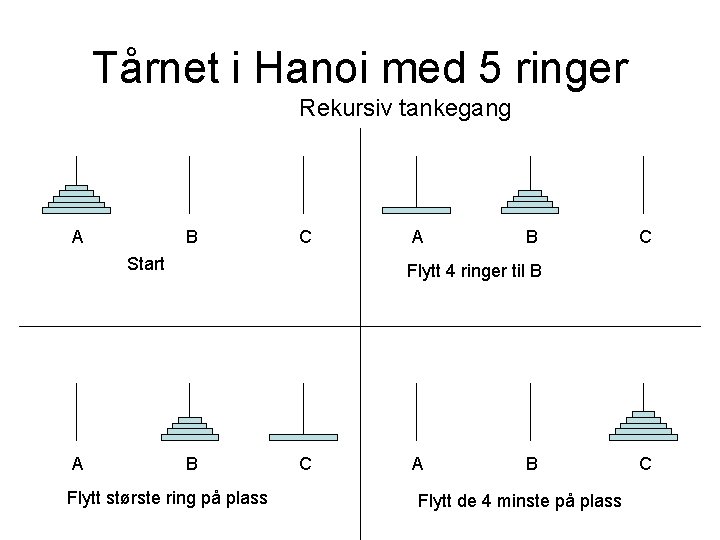
Tårnet i Hanoi med 5 ringer Rekursiv tankegang B A Start C A B Flytt 4 ringer til B C

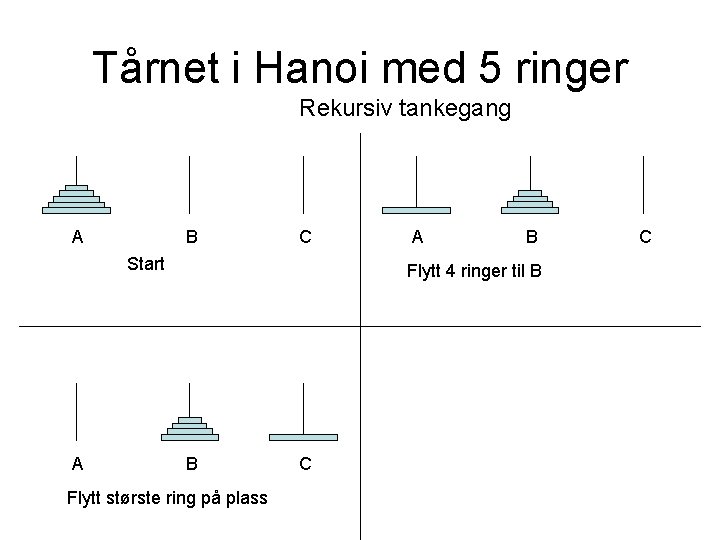
Tårnet i Hanoi med 5 ringer Rekursiv tankegang B A C Start A A B Flytt 4 ringer til B B Flytt største ring på plass C C

Tårnet i Hanoi med 5 ringer Rekursiv tankegang B A C Start A A B C Flytt 4 ringer til B B Flytt største ring på plass C A B Flytt de 4 minste på plass C

Finn summen av n tall

Finn summen av n tall • Løsning 1: Summen av n tall er summen av de n-1 første tallene pluss det siste

Finn summen av n tall • Løsning 1: Summen av n tall er summen av de n-1 første tallene pluss det siste • Løsning 2: Summen av n tall er summen av de n/2 første pluss summen av de n/2 siste

Finn summen av n tall • Løsning 1: Summen av n tall er summen av de n-1 første tallene pluss det siste • Løsning 2: Summen av n tall er summen av de n/2 første pluss summen av de n/2 siste • Løsning 3: Summen av n tall er summen av de n/2 tallene vi får når vi summerer to og to av dem

Finn summen av n tall • Løsning 1: Summen av n tall er summen av de n-1 første tallene pluss det siste • Løsning 2: Summen av n tall er summen av de n/2 første pluss summen av de n/2 siste • Løsning 3: Summen av n tall er summen av de n/2 tallene vi får når vi summerer to og to av dem • Se algoritme 2. 6 side 32

Finn en bestemt verdi i en sortert tabell - binærsøkealgoritmen • Sjekk midterste element – Hvis det er det vi leter etter, er vi ferdige – Hvis det vi leter etter er mindre, let videre i første halvdel – Hvis det vi leter etter er større, let videre i andre halvdel • Fortsett til vi enten finner det vi leter etter, eller vi ikke har flere plasser å lete • Eks: Finn 8 i tabellen 0, 2, 4, 5, 6, 8, 9, 13, 17

Kompleksitetsberegninger for rekursive algoritmer • Fakultetsalgoritmen: T(n) = T(n-1) + 1 • Tårnet i Hanoi: T(n) = 2 T(n-1) + 1 • Summasjonsalgoritmene – Løsning 1: T(n) = T(n-1) + 1 – Løsning 2: T(n) = 2 T(n/2) + 1 – Løsning 3: T(n) = T(n/2) + n/2 • Binærsøkealgoritmen: T(n) = T(n/2) + 1

Generell regel • Gjelder når vi har uttrykk på formen T(n) = a. T(n/b) + cnk • Hvis bk < a vil T(n) є Θ(nlogba) • Hvis bk = a vil T(n) є Θ(nklogn) • Hvis bk > a vil T(n) є Θ(nk)

Oppgaver • 2. 1 -2 side 28 • 2. 2 -7 side 39 • 2. 1 side 45