Introduction Un mcanismes est lassociation de plusieurs pices






















- Slides: 33

Introduction Un mécanismes est l'association de plusieurs pièces liées entre elles par des contacts physiques qui les rendent totalement ou partiellement solidaires, selon qu'ils autorisent ou non des mouvements relatifs. La liaison mécanique est le modèle utilisé pour décrire cette relation. Elle emploie des représentations mathématiques qui diffèrent suivant qu'on l'aborde sous différents aspects • Statique • Cinématique (étude des mouvements) X Réel Schématisé

Présentation Une liaison mécanique entre deux pièces existe s'il y a contact direct entre une ou plusieurs surfaces respectives de ces pièces. Il en résulte un ensemble de points de contact; ces points peuvent être isolés dans l'espace, disposés sur une ligne commune ou répartis sur une surface. Il existe différents types de surfaces de contact. Plan : Sphère :

Présentation Cylindre plein ou creux: Cône :

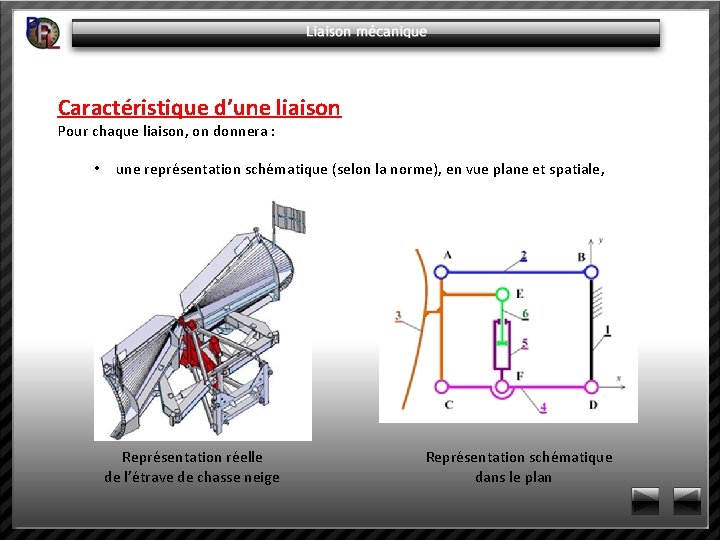
Caractéristique d’une liaison Pour chaque liaison, on donnera : • la dénomination normalisée de la liaison, avec sa référence centrée (permettant la construction du repère local avec directions principales par lequel sont distingués les degrés de liaison ou de liberté. Exemple liaison pivot

Caractéristique d’une liaison Pour chaque liaison, on donnera : • une représentation schématique (selon la norme), en vue plane et spatiale, Représentation réelle Représentation schématique de l’étrave de chasse neige dans le plan

Caractéristique d’une liaison Pour chaque liaison, on donnera : • les degrés de liaisons et les degrés de liberté suivant trois axes. Degrés de liberté d'une liaison: C'est le nombre de déplacements élémentaires indépendants autorisés par cette liaison. Degrés de liaison: C'est le nombre de déplacements élémentaires interdits. On notera que pour une liaison, la somme des degrés de liberté et des degrés de liaisons est égale à 6.

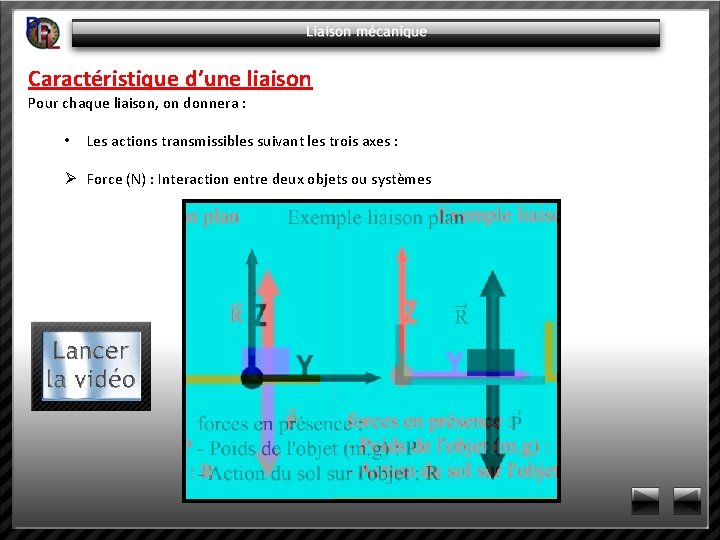
Caractéristique d’une liaison Pour chaque liaison, on donnera : • Les actions transmissibles suivant les trois axes : Ø Force (N) : Interaction entre deux objets ou systèmes

Caractéristique d’une liaison Pour chaque liaison, on donnera : • Les actions transmissibles suivant les trois axes : Ø Moment (Nm) : C’est l'effort en rotation appliqué à un axe. M (Nm) = F(N) x R (m) R F

Hypothèse d’étude Pour la suite de l’étude on partira du principe que les liaisons sont parfaites : • • Contacts sans frottement entre les surfaces ; Des surfaces de contact géométriquement parfaites ; Aucun jeu ; Toutes les pièces sont indéformables.

Liaison encastrement Axe Translation Rotation Force Moment X 0 0 1 1 Y 0 0 1 1 Z 0 0 1 1 Attendre animation, appuyer sur touche pour voir tableau

Liaison encastrement

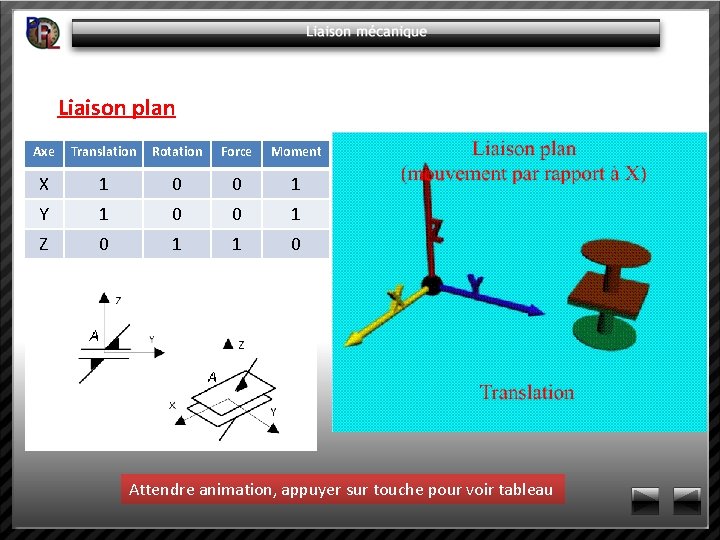
Liaison plan Axe Translation Rotation Force Moment X 1 0 0 1 Y 1 0 0 1 Z 0 1 1 0 Attendre animation, appuyer sur touche pour voir tableau

Liaison plan

Liaison rotule Axe Translation Rotation Force Moment X 0 1 1 0 Y 0 1 1 0 Z 0 1 1 0 Attendre animation, appuyer sur touche pour voir tableau

Liaison rotule

Liaison pivot Axe Translation Rotation Force Moment X 0 0 1 1 Y 0 1 1 0 Z 0 0 1 1 Attendre animation, appuyer sur touche pour voir tableau

Liaison pivot

Liaison pivot glissant Axe Translation Rotation Force Moment X 0 0 1 1 Y 1 1 0 0 Z 0 0 1 1 Attendre animation, appuyer sur touche pour voir tableau

Liaison pivot glissant

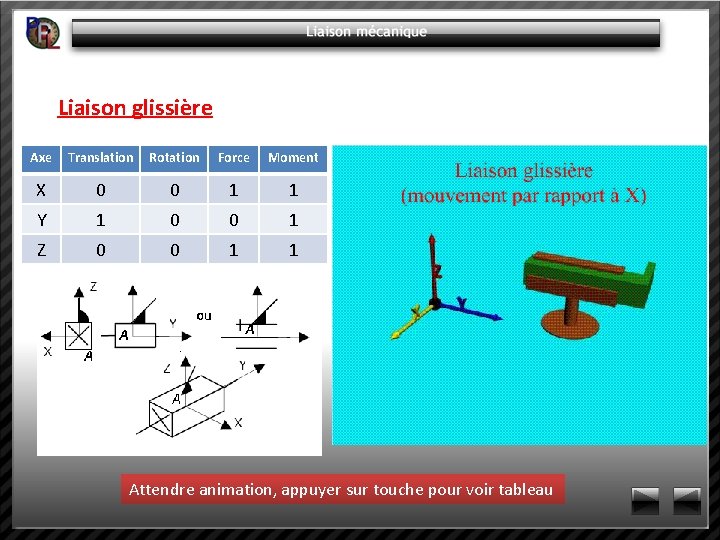
Liaison glissière Axe Translation Rotation Force Moment X 0 0 1 1 Y 1 0 0 1 Z 0 0 1 1 Attendre animation, appuyer sur touche pour voir tableau

Liaison glissière

Liaison hélicoïdale Axe Translation Rotation Force Moment X 0 0 1 1 Y 1 1 0 0 Z 0 0 1 1 Rotation et translation conjuguées Attendre animation, appuyer sur touche pour voir tableau

Liaison hélicoïdale

Liaison linéaire rectiligne Axe Translation Rotation Force Moment X 1 0 0 1 Y 1 1 0 0 Z 0 1 1 0 Attendre animation, appuyer sur touche pour voir tableau

Liaison linéaire rectiligne

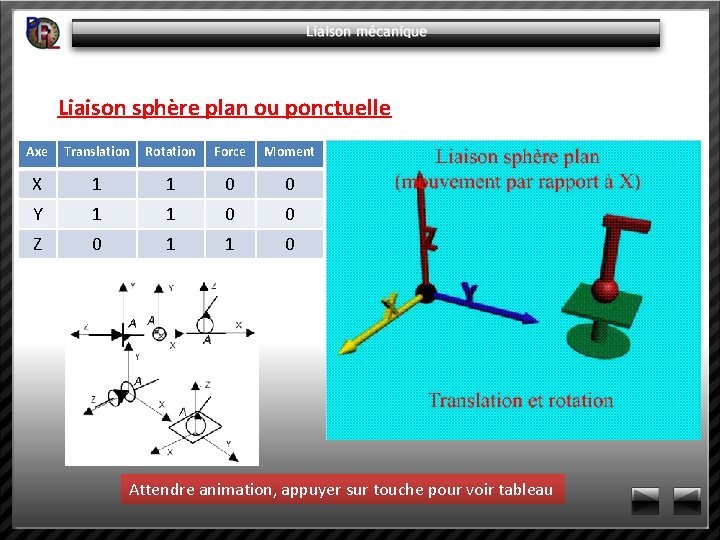
Liaison sphère plan ou ponctuelle Axe Translation Rotation Force Moment X 1 1 0 0 Y 1 1 0 0 Z 0 1 1 0 Attendre animation, appuyer sur touche pour voir tableau

Liaison sphère plan

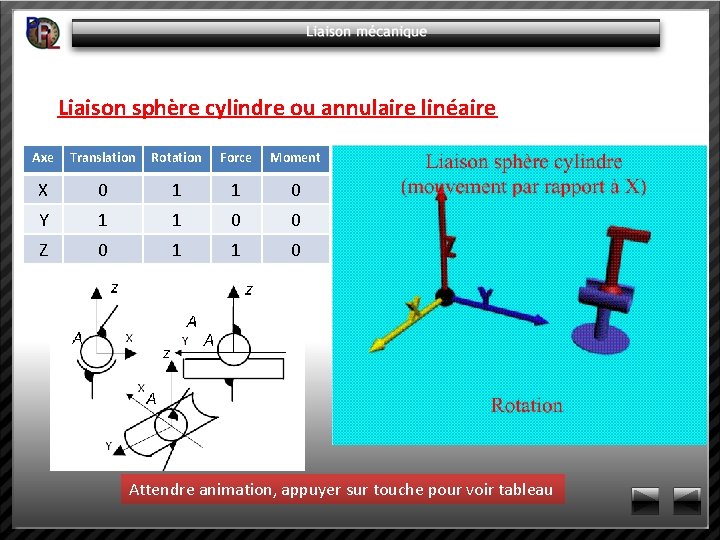
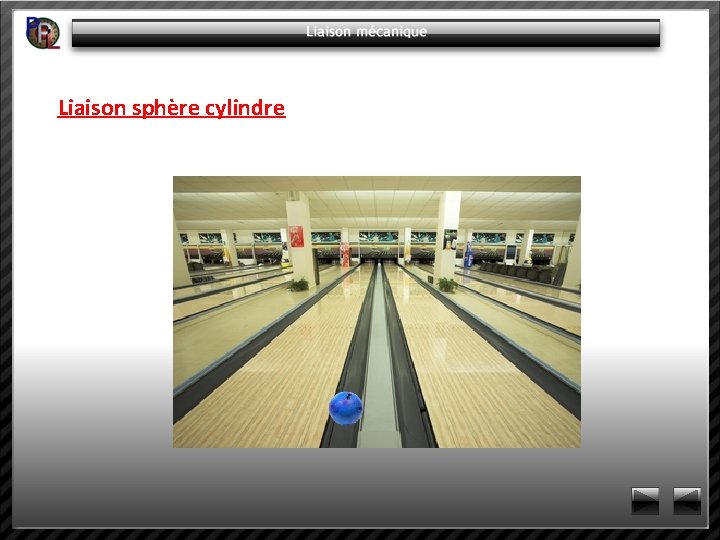
Liaison sphère cylindre ou annulaire linéaire Axe Translation Rotation Force Moment X 0 1 1 0 Y 1 1 0 0 Z 0 1 1 0 Attendre animation, appuyer sur touche pour voir tableau

Liaison sphère cylindre

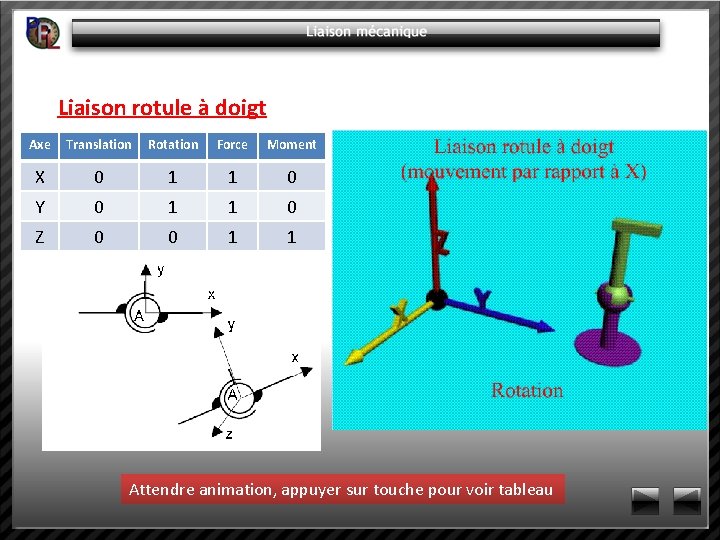
Liaison rotule à doigt Axe Translation Rotation Force Moment X 0 1 1 0 Y 0 1 1 0 Z 0 0 1 1 Attendre animation, appuyer sur touche pour voir tableau

Liaison rotule à doigt

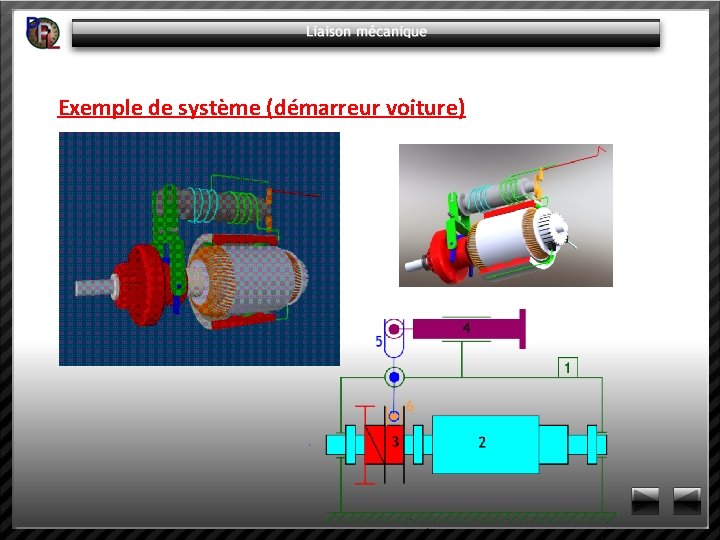
Exemple de système (démarreur voiture)

FIN
 Pices
Pices Liaison linéaire annulaire
Liaison linéaire annulaire Comparaison de 2 pourcentages
Comparaison de 2 pourcentages Echeance moyenne
Echeance moyenne Accord du verbe avec plusieurs sujets
Accord du verbe avec plusieurs sujets Lémuroidea
Lémuroidea Il est douteux que le metteur en scène où est l’acteur.
Il est douteux que le metteur en scène où est l’acteur. Quel est le nom de la femelle du sanglier
Quel est le nom de la femelle du sanglier Faites-vous du sport? oui, nous 1 of 1 faisons.
Faites-vous du sport? oui, nous 1 of 1 faisons. Alléluia alléluia christ est vivant ressuscité
Alléluia alléluia christ est vivant ressuscité Je suis tu es il est nous sommes vous êtes ils sont
Je suis tu es il est nous sommes vous êtes ils sont Qu'est ce que c'est
Qu'est ce que c'est Total float= * 1 point lst-est lst-eft est-lft eft-lst
Total float= * 1 point lst-est lst-eft est-lft eft-lst Seul le silence est grand
Seul le silence est grand Mon dieu tu es grand tu es beau lyrics
Mon dieu tu es grand tu es beau lyrics Dieu tu es grand tu es beau
Dieu tu es grand tu es beau Je suis tu es il est elle est
Je suis tu es il est elle est Gilles vigneault mon pays
Gilles vigneault mon pays Qu'est ce que c'est
Qu'est ce que c'est Appuyez sur l’image qui est dans le bon sens
Appuyez sur l’image qui est dans le bon sens Qu'est-ce que c'est un groupe nominal
Qu'est-ce que c'est un groupe nominal Verbe detat
Verbe detat Verbes qui exigent le subjonctif
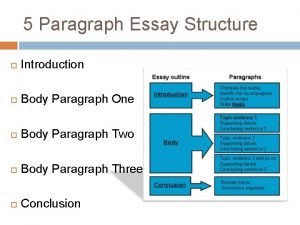
Verbes qui exigent le subjonctif Essay structure introduction
Essay structure introduction Sol ardet silentium est villa sub sole iacet
Sol ardet silentium est villa sub sole iacet Zany teninao ry tompo
Zany teninao ry tompo War poetry themes
War poetry themes Je suis tu es il est
Je suis tu es il est The rear guard poem
The rear guard poem Arcus ab imperatore dedicatus est
Arcus ab imperatore dedicatus est Nobis currendum est
Nobis currendum est Nobis currendum est
Nobis currendum est Divinum opus est sedare dolorem
Divinum opus est sedare dolorem Injection continue
Injection continue