Introduction This chapter focuses on vectors Vectors are

Introduction • This chapter focuses on vectors • Vectors are used to describe movement in a given direction • They are also used to describe straight lines in 3 D (in a similar way to y = mx + c being used for 2 D straight line graphs)

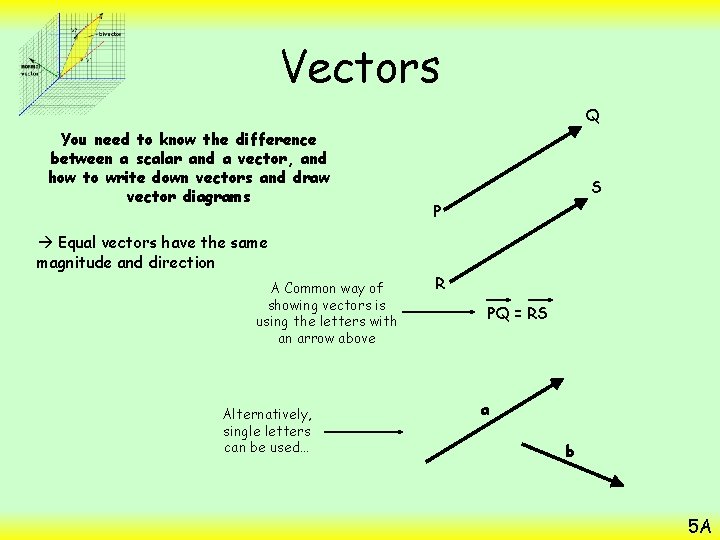
Vectors You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams Q Scalar Vector The distance from P to Q is 100 m From P to Q you go 100 m north P A scalar quantity has only a magnitude (size) A vector quantity has both a magnitude and a direction Direction and Magnitude Scalar A ship is sailing at 12 km/h N Vector 60° A ship is sailing at 12 km/h on a bearing of 060° 5 A

Vectors Q You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams Equal vectors have the same magnitude and direction A Common way of showing vectors is using the letters with an arrow above Alternatively, single letters can be used… S P R PQ = RS a b 5 A

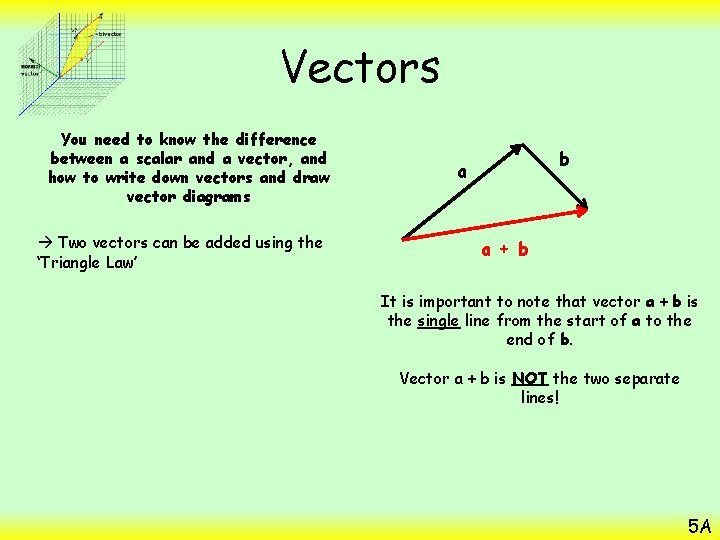
Vectors You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams Two vectors can be added using the ‘Triangle Law’ b a a + b It is important to note that vector a + b is the single line from the start of a to the end of b. Vector a + b is NOT the two separate lines! 5 A

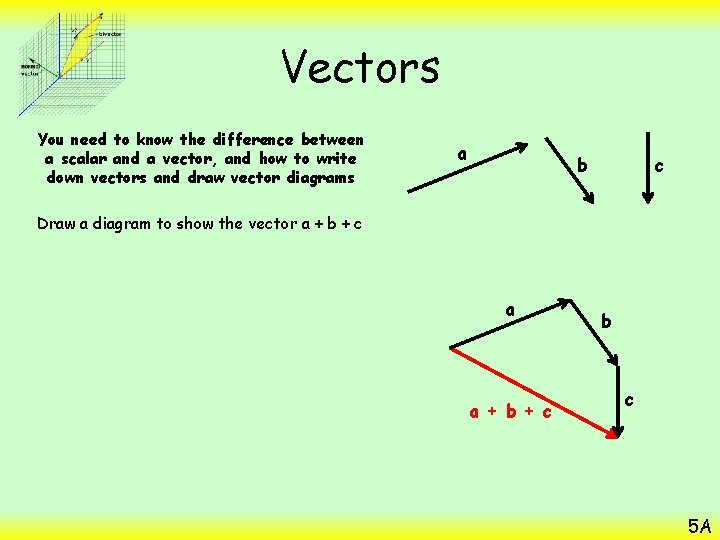
Vectors You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams a b c Draw a diagram to show the vector a + b + c a a + b + c b c 5 A

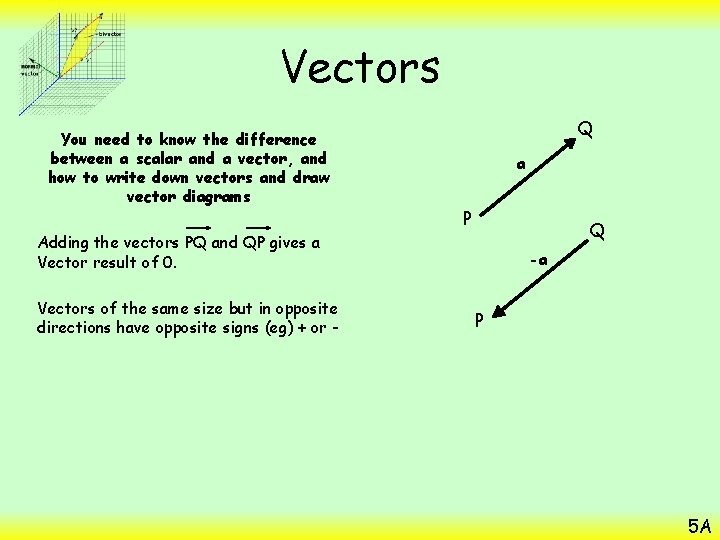
Vectors You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams Q a P Q Adding the vectors PQ and QP gives a Vector result of 0. Vectors of the same size but in opposite directions have opposite signs (eg) + or - -a P 5 A

Vectors a You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams a + b b The modulus value of a vector is another name for its magnitude Use Pythagoras’ Theorem Eg) The modulus of the Vector a is |a| The modulus of the vector PQ is |PQ| Question: The vector a is directed due east and |a| = 12. Vector b is directed due south and |b| = 5. Find |a + b| Square the shorter sides… Square Root 5 A

Vectors Q You need to know the difference between a scalar and a vector, and how to write down vectors and draw vector diagrams In the diagram opposite, find the following vectors in terms of a, b, c and d. a) PS = -a + c Or c - a b) RP = -b + a Or a - b c) PT = -a + b + d Or b + d - a d) TS = -d - b + c Or c - b - d a c P b S R d T 5 A

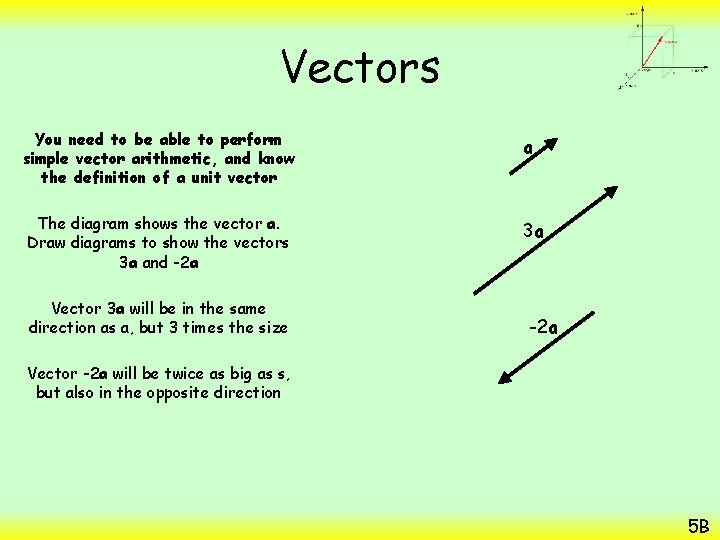
Vectors You need to be able to perform simple vector arithmetic, and know the definition of a unit vector a The diagram shows the vector a. Draw diagrams to show the vectors 3 a and -2 a 3 a Vector 3 a will be in the same direction as a, but 3 times the size -2 a Vector -2 a will be twice as big as s, but also in the opposite direction 5 B

Vectors You need to be able to perform simple vector arithmetic, and know the definition of a unit vector Any vector parallel to a may be written as λa, where λ (lamda) is a non-zero scalar (ie - represents a number…) Show that the vectors 6 a + 8 b and 9 a + 12 b are parallel… Factorise The second Vector is a multiple of the first, so they are parallel. In this case, λ is 3/2 or 1. 5 5 B

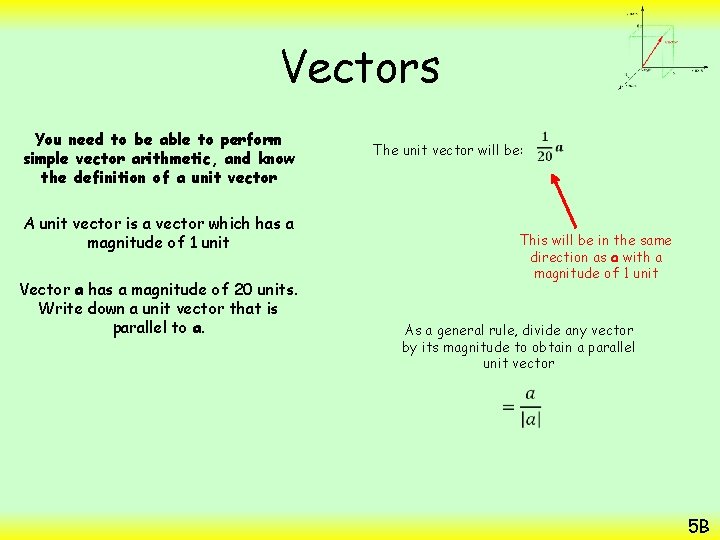
Vectors You need to be able to perform simple vector arithmetic, and know the definition of a unit vector The unit vector will be: A unit vector is a vector which has a magnitude of 1 unit Vector a has a magnitude of 20 units. Write down a unit vector that is parallel to a. This will be in the same direction as a with a magnitude of 1 unit As a general rule, divide any vector by its magnitude to obtain a parallel unit vector 5 B

Vectors You need to be able to perform simple vector arithmetic, and know the definition of a unit vector Given that: Find the values of the scalars s and t If: Comparing coefficients: And the vectors a and b are not parallel and non-zero, then: and Effectively, if the two vectors are equal then the coefficients of a and b must also be equal 1) 2) Add the equations together Divide by 3 Sub into either of 1) or 2) to find the value of t 5 B

Vectors You need to be able to perform simple vector arithmetic, and know the definition of a unit vector In the diagram opposite, PQ = 3 a, QR = b, P b-a k(3 a+b) S 3 a Q X 4 a b R SR = 4 a and PX = k. PR. Find in terms of a, b and k: a) PS = 3 a + b – 4 a b) PX = k. PR = b–a = k(3 a + b) c) SQ = 4 a - b d) SX = -b + a + k(3 a + b) = -b + a + 3 ka + kb = (3 k + 1)a + (k – 1)b Multiply out the bracket Group up and factorise the ‘a’ and ‘b’ terms separately 5 B

Vectors P You need to be able to perform simple vector arithmetic, and know the definition of a unit vector 3 a Q b X S e) Use the fact that X lies on SQ to find the value of k 4 a R SX = (3 k + 1)a + (k – 1)b SQ = 4 a - b Since X is on SQ, SX and SQ are parallel, ie) one is a multiple of another! 1) 2) x 4 Multiply out the bracket Use the lamda symbol to represent one being a multiple of the other… Add together Solve for k 5 B

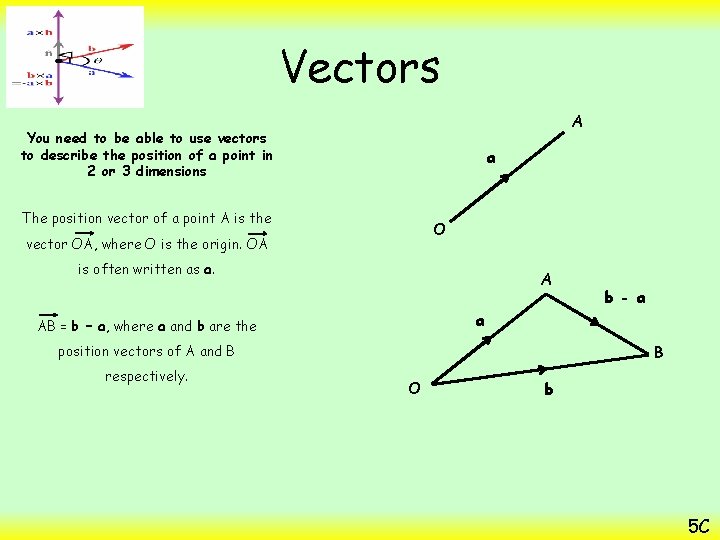
Vectors A You need to be able to use vectors to describe the position of a point in 2 or 3 dimensions a The position vector of a point A is the O vector OA, where O is the origin. OA is often written as a. A a AB = b – a, where a and b are the B position vectors of A and B respectively. b - a O b 5 C

Vectors You need to be able to use vectors to describe the position of a point in 2 or 3 dimensions 1/ A 3(b 1 – a) 2/ P b-a 3(b – a) 2 a In the diagram, points A and B have B position vectors a and b respectively. The point P divides AB in the ratio 1: 2. b O Find the position vector of P. Using the rule we just saw… If the line is split in the ratio 1: 2, then one part is 1/3 and the other is 2/3 The position vector of P is how we get from O to P 5 C

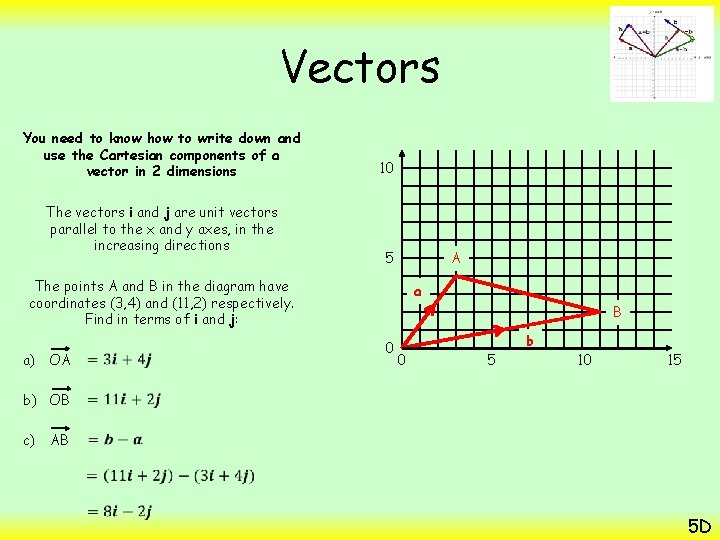
Vectors You need to know how to write down and use the Cartesian components of a vector in 2 dimensions The vectors i and j are unit vectors parallel to the x and y axes, in the increasing directions 10 5 A The points A and B in the diagram have coordinates (3, 4) and (11, 2) respectively. Find in terms of i and j: a) OA b) OB c) AB a B 0 0 5 b 10 15 5 D

Vectors Given that: a = 2 i + 5 j b = 12 i – 10 j c = -3 i + 9 j You need to know how to write down and use the Cartesian components of a vector in 2 dimensions You can write a vector with Cartesian components as a column matrix: Find a + b + c Column matrix notation can be easier to read and avoids the need to write out lots of i and j terms. Be careful with negatives! 5 D

Vectors You need to know how to write down and use the Cartesian components of a vector in 2 dimensions The vector a is equal to 5 i - 12 j. Find |a| and find a unit vector in the same direction as a. 5 i The modulus (magnitude) of xi + yj is: 12 j 5 i – 12 j xi + yj yj xi This comes from Pythagoras’ Theorem Alternative notation… 5 D

Vectors You need to know how to write down and use the Cartesian components of a vector in 2 dimensions Given that a = 5 i + j and b = -2 i – 4 j, find the exact value of |2 a + b| The modulus (magnitude) of xi + yj is: Use x = 8 and y = -2 ‘Exact’ means you can leave in surd form 5 D

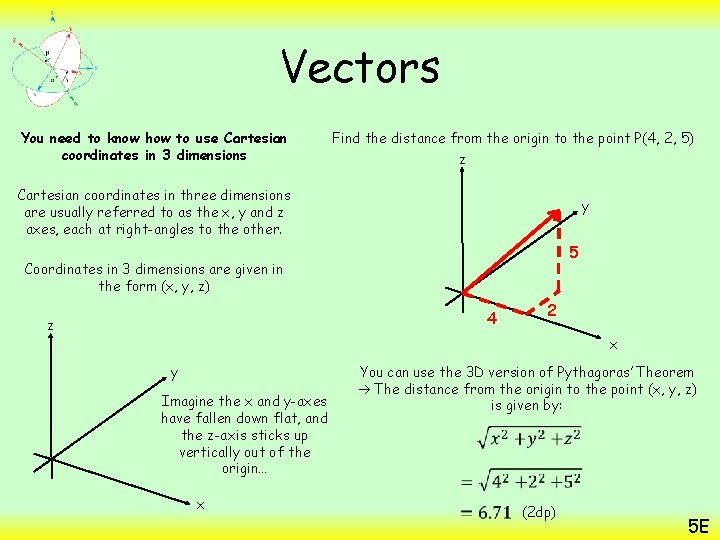
Vectors You need to know how to use Cartesian coordinates in 3 dimensions Find the distance from the origin to the point P(4, 2, 5) z Cartesian coordinates in three dimensions are usually referred to as the x, y and z axes, each at right-angles to the other. y 5 Coordinates in 3 dimensions are given in the form (x, y, z) 4 z 2 x y Imagine the x and y-axes have fallen down flat, and the z-axis sticks up vertically out of the origin… x You can use the 3 D version of Pythagoras’ Theorem The distance from the origin to the point (x, y, z) is given by: (2 dp) 5 E

Vectors You need to know how to use Cartesian coordinates in 3 dimensions Cartesian coordinates in three dimensions are usually referred to as the x, y and z axes, each at right-angles to the other. Find the distance between the points A(1, 3, 4) and B(8, 6, -5) First calculate the vector from A to B Coordinates in 3 dimensions are given in the form (x, y, z) z y Then use 3 D Pythagoras x (1 dp) 5 E

Vectors You need to know how to use Cartesian coordinates in 3 dimensions Cartesian coordinates in three dimensions are usually referred to as the x, y and z axes, each at right-angles to the other. Coordinates in 3 dimensions are given in the form (x, y, z) The coordinates of A and B are (5, 0, 3) and (4, 2, k) respectively. Given that |AB| is 3 units, find the possible values of k Calculate AB using k Use Pythagoras in 3 D z Careful when squaring the bracket y |AB| = 3 Square both sides Solve as a quadratic x 5 E

Vectors You can extend the two dimensional vector results to 3 dimensions, using k as the unit vector parallel to the zaxis The vectors i, j and k are unit vectors parallel to the x, y and zaxes in the increasing directions The vector xi + yj + zk can be written as a column matrix: The points A and B have position vectors 4 i + 2 j + 7 k and 3 i + 4 j – k respectively. Find |AB| and show that triangle OAB is isosceles. The modulus (magnitude) of xi + yj + zk is given by: Find the vector AB Now find the magnitude of AB Find the magnitude of OA and OB using their position vectors Isosceles as 2 vectors are equal… 5 F

Vectors You can extend the two dimensional vector results to 3 dimensions, using k as the unit vector parallel to the zaxis a) Find |AB| Calculate the vector AB The points A and B have the coordinates (t, 5, t-1) and (2 t, t, 3) respectively. a) Find |AB| b) By differentiating |AB|2, find the value of t for which |AB| is a minimum c) Hence, find the minimum value of |AB| Find the magnitude of AB in terms of t Careful with the bracket expansion! 5 F

Vectors You can extend the two dimensional vector results to 3 dimensions, using k as the unit vector parallel to the zaxis The points A and B have the coordinates (t, 5, t-1) and (2 t, t, 3) respectively. a) Find |AB| b) By differentiating |AB|2, find the value of t for which |AB| is a minimum c) Hence, find the minimum value of |AB| b) By differentiating |AB|2, find the value of t for which |AB| is a minimum Square both sides Differentiate (often p is used to represent the vector) Set equal to 0 for a minimum Solve The value of t = 3 is the value for which the distance between the points A and B is the smallest. . It is possible to do this by differentiating |AB| rather than |AB|2, but it can be more difficult! 5 F

Vectors You can extend the two dimensional vector results to 3 dimensions, using k as the unit vector parallel to the zaxis The points A and B have the coordinates (t, 5, t-1) and (2 t, t, 3) respectively. c) Hence, find the minimum value of |AB| Sub in the value of t a) Find |AB| b) By differentiating find the value of t for which |AB| is a minimum |AB|2, c) Hence, find the minimum value of |AB| (2 dp) So for the given coordinates, the closest that points A and B could be is 3. 74 units apart, when t = 3. 5 F

Vectors a You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors 30° X b On the diagram to the right, the angle between a and b is θ. The two vectors must be directed away from point X a 20° X On the second diagram, vector b is directed towards X. Hence, the angle between the two vectors is 160°. b a This comes from re-drawing the diagram with vector b pointing away from point X. 160° b X 20° b 5 G

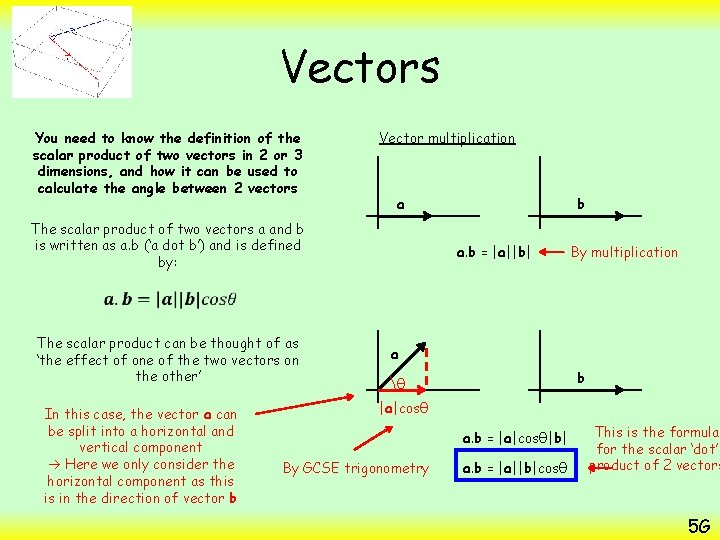
Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors Vector multiplication a The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: b a. b = |a||b| By multiplication The scalar product can be thought of as ‘the effect of one of the two vectors on the other’ In this case, the vector a can be split into a horizontal and vertical component Here we only consider the horizontal component as this is in the direction of vector b a b θ |a|cosθ a. b = |a|cosθ|b| By GCSE trigonometry a. b = |a||b|cosθ This is the formula for the scalar ‘dot’ product of 2 vectors 5 G

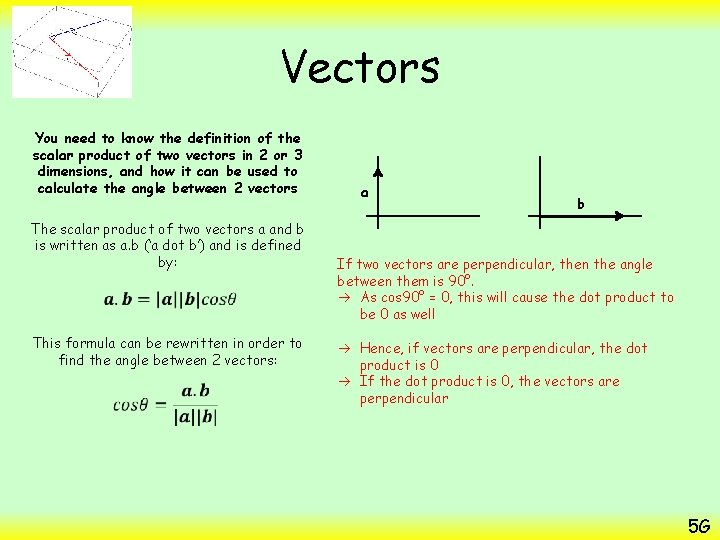
Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: This formula can be rewritten in order to find the angle between 2 vectors: a b If two vectors are perpendicular, then the angle between them is 90°. As cos 90° = 0, this will cause the dot product to be 0 as well Hence, if vectors are perpendicular, the dot product is 0 If the dot product is 0, the vectors are perpendicular 5 G

Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: If a = x 1 i + y 1 j + z 1 k and b = x 2 i + y 2 j + z 2 k Then: This formula can be rewritten in order to find the angle between 2 vectors: This is a way to find the dot product from 2 vectors If we are to use this formula to work out the angle between 2 vectors, we therefore need an alternative way to calculate the scalar product… 5 G

Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: This formula can be rewritten in order to find the angle between 2 vectors: Given that a = 8 i – 5 j – 4 k and b = 5 i + 4 j – k: a) Find a. b Use the dot product formula If a = x 1 i + y 1 j + z 1 k and b = x 2 i + y 2 j + z 2 k Then: 5 G

Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: This formula can be rewritten in order to find the angle between 2 vectors: Given that a = 8 i – 5 j – 4 k and b = 5 i + 4 j – k: a) Find a. b b) Calculate the angle between vectors a and b Use the angle formula – you will need to calculate the magnitude of each vector as well… If a = x 1 i + y 1 j + z 1 k and b = x 2 i + y 2 j + z 2 k Then: Sub in the values Solve, remembering to use inverse Cos 5 G

Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors The scalar product of two vectors a and b is written as a. b (‘a dot b’) and is defined by: This formula can be rewritten in order to find the angle between 2 vectors: Given that the vectors a = 2 i – 6 j + k and b = 5 i + 2 j + λk are perpendicular, calculate the value of λ. If a = x 1 i + y 1 j + z 1 k and b = x 2 i + y 2 j + z 2 k Calculate the dot product in terms of λ As the vectors are perpendicular, the dot product must be 0 Solve Then: Only this value of λ will cause these vectors to be perpendicular… 5 G

Vectors You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors Let the required vector be xi + yj + zk Given that a = -2 i + 5 j - 4 k and b = 4 i 8 j + 5 k, find a vector which is perpendicular to both a and b The dot products of both a and b with the required vector will be 0 and Choosing a different value for z will lead to a vector that is a different size, but which is still pointing in the same direction (ie – perpendicular) Let z=1 x 2 Now solve as simultaneous equations However, this will not work if you choose z = 0 So a possible answer would be: x 4 5 G

Vectors Link to Autograph You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors Given that a = -2 i + 5 j - 4 k and b = 4 i 8 j + 5 k, find a vector which is perpendicular to both a and b The 3 D axes show the 3 vectors in question. The green vector is perpendicular to both the others, but you can only see this clearly when it is rotated! 5 G

Vectors Link to Autograph You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors On this example, the second picture shows the diagram being viewed from the top of the red vector 5 G

Vectors Link to Autograph You need to know the definition of the scalar product of two vectors in 2 or 3 dimensions, and how it can be used to calculate the angle between 2 vectors On this example, the second picture shows the diagram being viewed from the top of the red vector The vectors do not need to be touching – it is always possible to find a vector that is perpendicular to 2 others! 5 G

Vectors y You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) Let us first consider how this is done in 2 dimensions x So any linear 2 D graph needs a direction, and a point on the line With just the direction, the line wouldn’t have a specific path and could effectively be anywhere With only a given point, the line would not have a specific direction m is the gradient of the line This can also be thought of as the DIRECTION the line goes c is the y-intercept This is a given point on the line 5 H

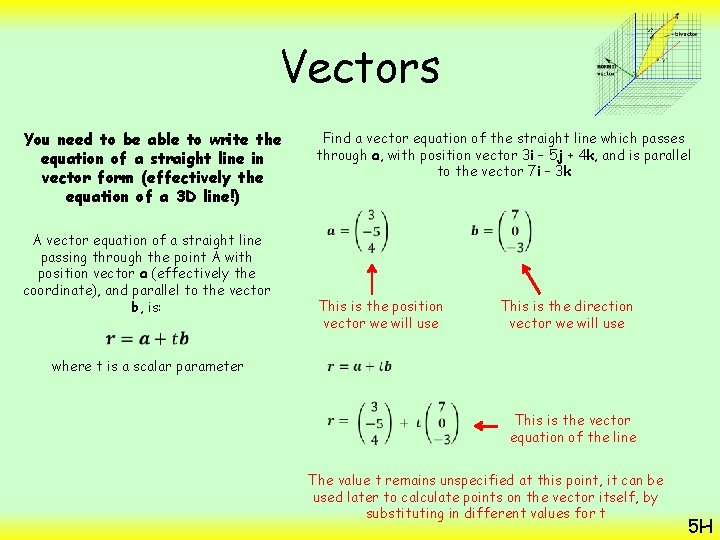
Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) In 3 D, we effectively need the same bits of information A vector equation of a straight line passing through the point A with position vector a (effectively the coordinate), and parallel to the vector b, is: where t is a scalar parameter We need any point on the line (ie – a coordinate in the form (x, y, z)) We also need to know the direction the line is travelling (a vector with terms i, j and k) 5 H

Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) Find a vector equation of the straight line which passes through a, with position vector 3 i – 5 j + 4 k, and is parallel to the vector 7 i – 3 k A vector equation of a straight line passing through the point A with position vector a (effectively the coordinate), and parallel to the vector b, is: where t is a scalar parameter This is the position vector we will use This is the direction vector we will use This is the vector equation of the line The value t remains unspecified at this point, it can be used later to calculate points on the vector itself, by substituting in different values for t 5 H

Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) A vector equation of a straight line passing through the point A with position vector a (effectively the coordinate), and parallel to the vector b, is: Some alternative forms (By writing in a different form) (By multiplying out the brackets and then regrouping i, j and k terms) where t is a scalar parameter (By rewriting again in the original column vector form) 5 H

Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) Working in 2 D – the equation of the line can be calculated by using either: a) The gradient (direction) and a coordinate (like we just did) b) Two coordinates (since you can calculate the gradient between them) 3 D can also be done either way… Find a vector equation of the straight line passing through the points A and B, with coordinates (4, 5, -1) and (6, 3, 2) respectively. Calculating b – a will give you the vector AB, ie) the direction vector that passes through A and B A vector equation of a straight line passing through the points A and B, with position vectors a and b respectively, is given by: where t is a scalar parameter As you aren’t given the direction vector in this type, you have to work it out by calculating the vector AB (b – a) Then use (b – a) along with either of the 2 coordinates/position vectors you’re given 5 H

Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) A vector equation of a straight line passing through the points A and B, with position vectors a and b respectively, is given by: The straight line l has a vector equation: r = (3 i + 2 j – 5 k) + t(i – 6 j – 2 k) Given that the point (a, b, 0) lies on l, calculate the values of a and b The top numbers give the x coordinate, the middles give the y, and the bottom gives the z, all for an unknown value of t (at this point) where t is a scalar parameter As you aren’t given the direction vector in this type, you have to work it out by calculating the vector AB (b – a) We can use the bottom equation to find the value of t The coordinate itself is (0. 5, 17, 0) 5 H

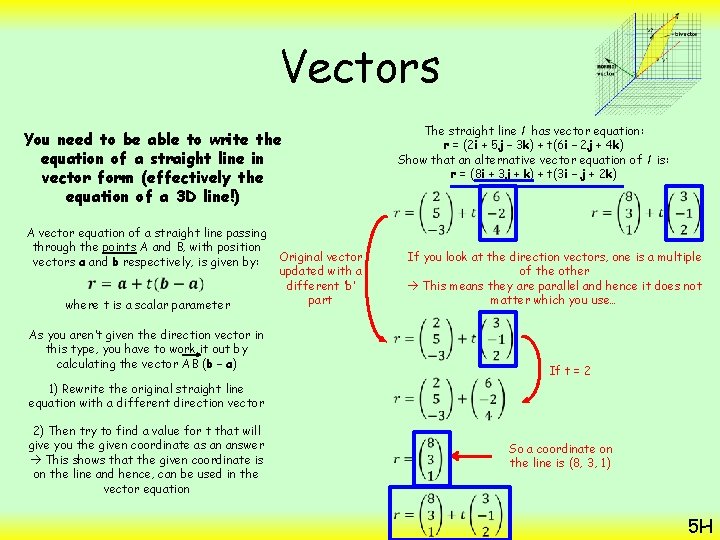
Vectors You need to be able to write the equation of a straight line in vector form (effectively the equation of a 3 D line!) The straight line l has vector equation: r = (2 i + 5 j – 3 k) + t(6 i – 2 j + 4 k) Show that an alternative vector equation of l is: r = (8 i + 3 j + k) + t(3 i – j + 2 k) A vector equation of a straight line passing through the points A and B, with position Original vectors a and b respectively, is given by: updated with a different ‘b’ part where t is a scalar parameter As you aren’t given the direction vector in this type, you have to work it out by calculating the vector AB (b – a) 1) Rewrite the original straight line equation with a different direction vector 2) Then try to find a value for t that will give you the given coordinate as an answer This shows that the given coordinate is on the line and hence, can be used in the vector equation If you look at the direction vectors, one is a multiple of the other This means they are parallel and hence it does not matter which you use… If t = 2 So a coordinate on the line is (8, 3, 1) 5 H

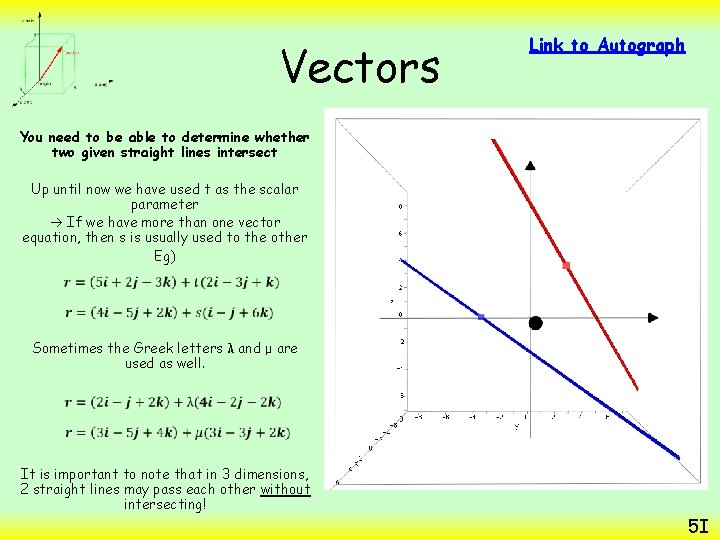
Vectors Link to Autograph You need to be able to determine whether two given straight lines intersect Up until now we have used t as the scalar parameter If we have more than one vector equation, then s is usually used to the other Eg) Sometimes the Greek letters λ and μ are used as well. It is important to note that in 3 dimensions, 2 straight lines may pass each other without intersecting! 5 I

Vectors You need to be able to determine whether two given straight lines intersect It is important to note that in 3 dimensions, 2 straight lines may pass each other without intersecting! 1 a) Show that the lines with vector equations: r = (3 i + 8 j – 2 k) + t(2 i – j + 3 k) and r = (7 i + 4 j + 3 k) + s(2 i + j + 4 k) intersect. Find the x, y and z coordinates in terms of t and s If there is a point of intersection, then at this point the equations for the x, y and z coordinates in terms of t and s will be equal… Solve 2 of the equations simultaneously, and then check if the answers also satisfy the third rearrange Solve simultaneously by making either the t or s terms ‘equal’ Sub s and t into the 3 rd pair – if it ‘works’ then the lines intersect. If not, then they don’t… So the lines DO intersect 5 I

Vectors You need to be able to determine whether two given straight lines intersect It is important to note that in 3 dimensions, 2 straight lines may pass each other without intersecting! Sub t = 3 into the first equation and calculate the position vector 1 a) Show that the lines with vector equations: r = (3 i + 8 j – 2 k) + t(2 i – j + 3 k) and r = (7 i + 4 j + 3 k) + s(2 i + j + 4 k) intersect. We have just calculated that the above lines intersect for the values of t = 3 and s = 1 b) Calculate the position vector of the point of intersection Sub s = 1 into the second equation and calculate the position vector You only need to choose one of the equations for the substitution, as you can see, it works for both! 5 I

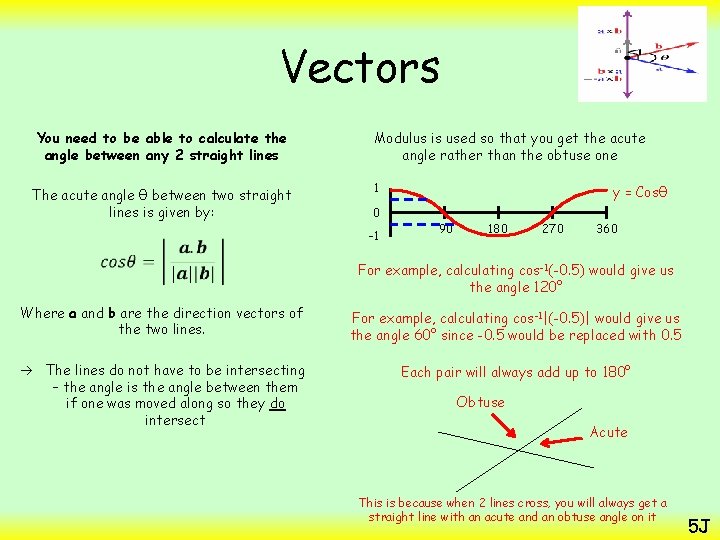
Link to Autograph Vectors You need to be able to calculate the angle between any 2 straight lines The acute angle θ between two straight lines is given by: Where a and b are the direction vectors of the two lines. The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect Eg) The lines to the right do not intersect, but the angle calculated is the angle between them if one was translated such that they do intersect 5 J

Vectors You need to be able to calculate the angle between any 2 straight lines The acute angle θ between two straight lines is given by: Modulus is used so that you get the acute angle rather than the obtuse one 1 0 -1 y = Cosθ 90 180 270 360 For example, calculating cos-1(-0. 5) would give us the angle 120° Where a and b are the direction vectors of the two lines. For example, calculating cos-1|(-0. 5)| would give us the angle 60° since -0. 5 would be replaced with 0. 5 The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect Each pair will always add up to 180° Obtuse Acute This is because when 2 lines cross, you will always get a straight line with an acute and an obtuse angle on it 5 J

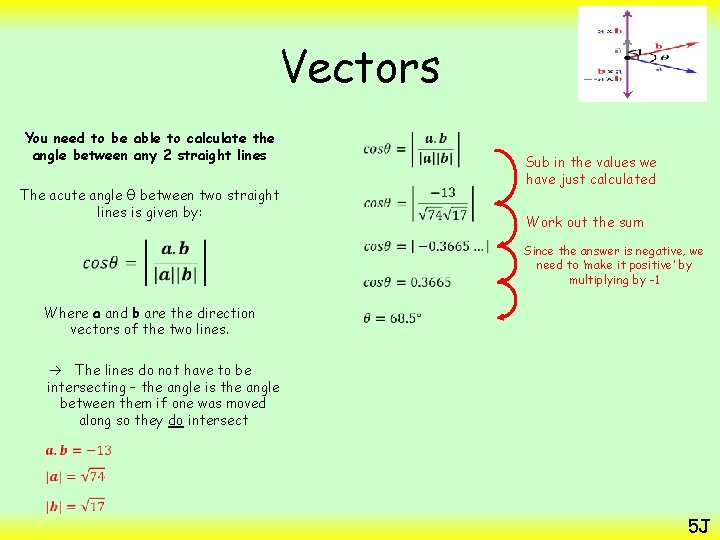
Vectors You need to be able to calculate the angle between any 2 straight lines Find the acute angle between the lines with vector equations: r = (2 i + j + k) + t(3 i – 8 j – k) and r = (7 i + 4 j + k) + s(2 i + 2 j + 3 k) The acute angle θ between two straight lines is given by: To do this, you only need the direction vectors Where a and b are the direction vectors of the two lines. The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect Calculate the dot product, a. b Calculate the magnitude of a and b 5 J

Vectors You need to be able to calculate the angle between any 2 straight lines The acute angle θ between two straight lines is given by: Work out the sum Where a and b are the direction vectors of the two lines. Sub in the values we have just calculated Since the answer is negative, we need to ‘make it positive’ by multiplying by -1 The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect 5 J

Summary • We have learnt a great deal about vectors this chapter • We have seen that when vectors are perpendicular, their dot ‘scalar’ product is equal to 0 • We have looked at the vector equation of a straight line • We have seen how to calculate the angle between 2 lines • We have learnt how to calculate whether 2 vectors intersect