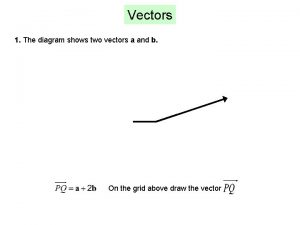
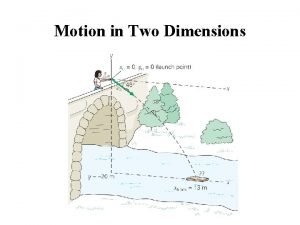
Vectors in Two Dimensions Read Chapter 1 6

Vectors in Two Dimensions Read Chapter 1. 6 -1. 9

Scalars and Vectors All measurements are considered to be quantities. In physics, there are 2 types of quantities – SCALARS AND VECTORS. Scalar quantities have only magnitude. time mass temperature Vector quantities have magnitude and direction. displacement acceleration Force velocity Gravitational Field Magnetic Field

Vectors are used to describe motion and solve problems concerning motion. For this reason, it is critical that you have an understanding of how to represent vectors add vectors subtract vectors manipulate vector quantities. in 2 and 3 dimensions.

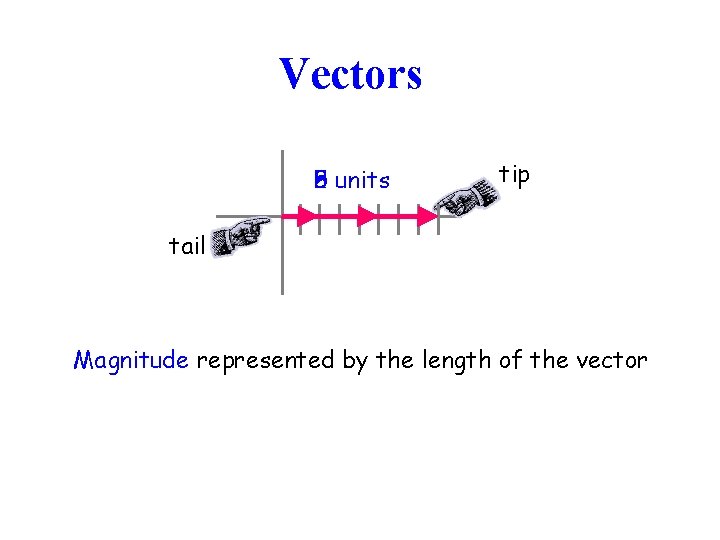
Vectors 8 units 5 2 tip tail Magnitude represented by the length of the vector

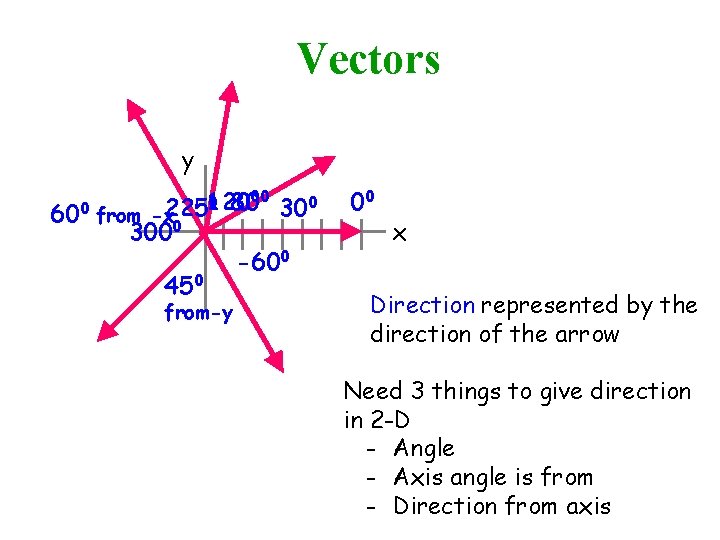
Vectors y 600 00 0 80 120 225 300 from -x 3000 -600 450 from-y 00 x Direction represented by the direction of the arrow Need 3 things to give direction in 2 -D - Angle - Axis angle is from - Direction from axis

Adding Vectors We know how to add vectors in 1 -dimension. Example: displacement. If someone walks 4 mi east (Dx 1) and then 7 mi west (Dx 2) the total displacement (Dx 1 + Dx 2) is 3 mi west. 1. Adding vectors GRAPHICALLY – place them TAIL TO TIP west Dx 1 + Dx 2 = 3 mi west -3 -2 -1 Dx 2 = 7 mi W Dx 1 = 4 mi E 0 1 2 3 4 2. Adding vectors MATHEMATICALLY – In 1 - dimension, assign direction + or – and add algebraically Dx 1 + Dx 2 = +4 mi + (-7 mi) = -3 mi east

Adding Vectors v 1 = 5 What about if the vectors are in different directions in 2 -D? How do we describe the direction? How do we add/subtract the vectors? 50 o above +x v 2 35 o below +x =3

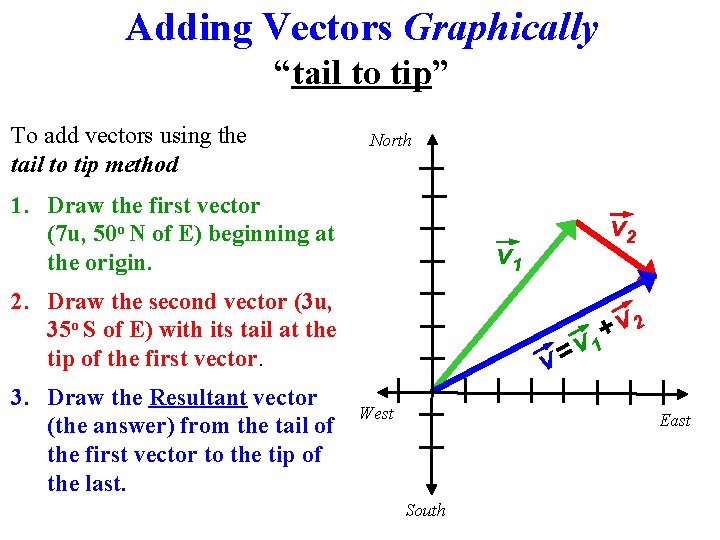
Adding Vectors Graphically “tail to tip” To add vectors using the tail to tip method North 1. Draw the first vector (7 u, 50 o N of E) beginning at the origin. v 1 2. Draw the second vector (3 u, 35 o S of E) with its tail at the tip of the first vector. 3. Draw the Resultant vector (the answer) from the tail of the first vector to the tip of the last. v 2 v= West v 2 + v 1 East South

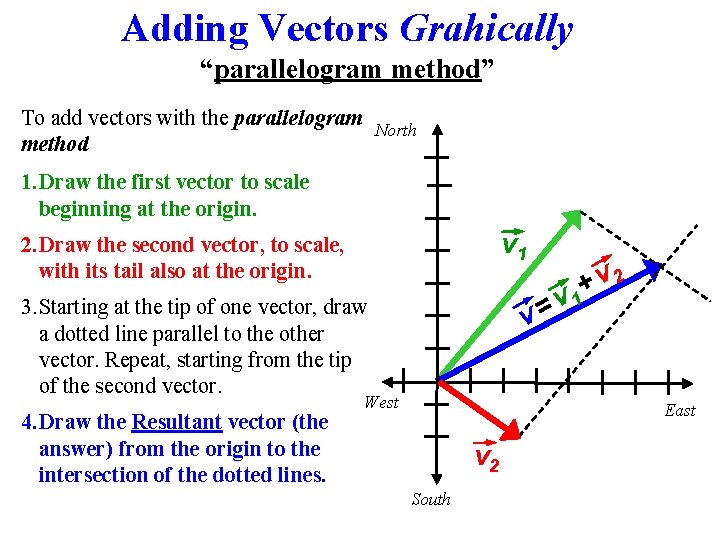
Adding Vectors Grahically “parallelogram method” To add vectors with the parallelogram North method 1. Draw the first vector to scale beginning at the origin. v 1 2. Draw the second vector, to scale, with its tail also at the origin. v= 3. Starting at the tip of one vector, draw a dotted line parallel to the other vector. Repeat, starting from the tip of the second vector. 4. Draw the Resultant vector (the answer) from the origin to the intersection of the dotted lines. West v 2 + v 1 East v 2 South

Adding Vectors Mathematically What if the vectors are in different directions? For example, what if I walk 5 steps north and then 4 steps east. What is my total displacement , Dx, for the trip? OR what is the vector sum of the Dx 1 and Dx 2? Dx 2 =4 steps east Dx 1= 5 steps north D x = D x 1+ D x 2 = ?

Adding Vectors Mathematically 4 steps east 5 steps north q Use Pythagorean Theorem to find the magnitude of Dx Dx = ? Use right triangle trig to find the direction of Dx

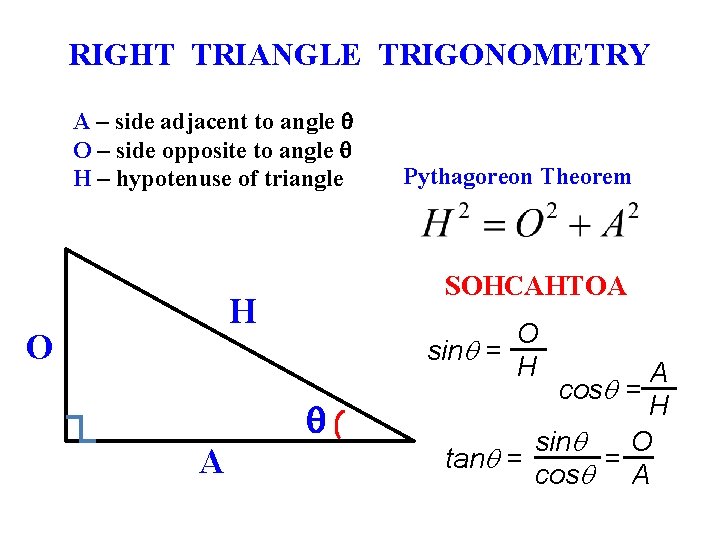
RIGHT TRIANGLE TRIGONOMETRY A – side adjacent to angle q O – side opposite to angle q H – hypotenuse of triangle SOHCAHTOA H O O sinq = H q A Pythagoreon Theorem A cosq = H sinq O tanq = = cosq A

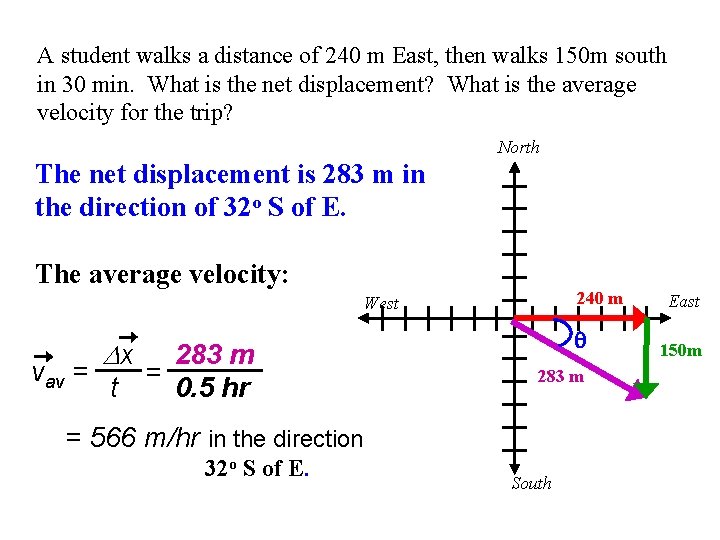
A student walks a distance of 240 m East, then walks 150 m south in 30 min. What is the net displacement? What is the average velocity for the trip? MAGNITUDE R 2 = A 2 +B 2 = 2402 + 1502 North R = 283 m DIRECTION opp 150 m tanq = = adj 240 m tanq = 0. 625 A = 240 m West R= q= tan-1(1. 3) = 32 o south of east Notice that A and B are perpendicular components of R. They are the amount of R in each direction South q 28 3 m East B= 150 m

A student walks a distance of 240 m East, then walks 150 m south in 30 min. What is the net displacement? What is the average velocity for the trip? North The net displacement is 283 m in the direction of 32 o S of E. The average velocity: 240 m West Dx 283 m vav = = t 0. 5 hr q 283 m = 566 m/hr in the direction 32 o S of E. South East 150 m

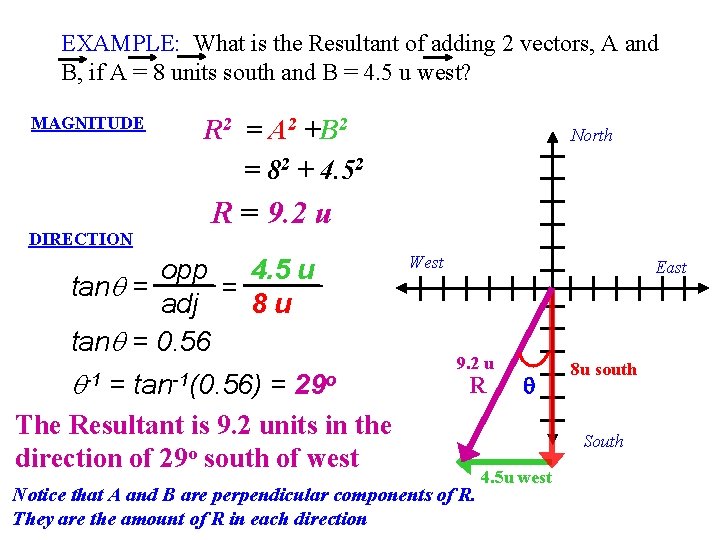
EXAMPLE: What is the Resultant of adding 2 vectors, A and B, if A = 8 units south and B = 4. 5 u west? MAGNITUDE DIRECTION R 2 = A 2 +B 2 = 82 + 4. 52 R = 9. 2 u opp 4. 5 u tanq = = adj 8 u tanq = 0. 56 q = = The Resultant is 9. 2 units in the direction of 29 o south of west -1 North tan-1(0. 56) 29 o West East 9. 2 u R Notice that A and B are perpendicular components of R. They are the amount of R in each direction q 8 u south South 4. 5 u west

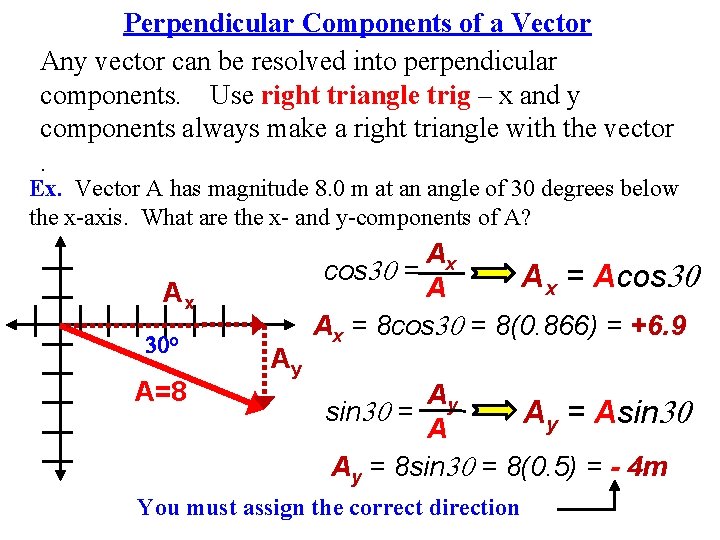
Perpendicular Components of a Vector Any vector can be resolved into perpendicular components. Use right triangle trig – x and y components always make a right triangle with the vector. Ex. Vector A has magnitude 8. 0 m at an angle of 30 degrees below the x-axis. What are the x- and y-components of A? Ax 30 o A=8 Ay Ax cos 30 = Ax = Acos 30 A Ax = 8 cos 30 = 8(0. 866) = +6. 9 Ay sin 30 = Asin 30 y A Ay = 8 sin 30 = 8(0. 5) = - 4 m You must assign the correct direction

x- and y- Components of a Vector What are the x- and y- components of the vector A, shown below? y Ax = Acosq = 10 cos(30) = 10(0. 866) = -8. 7 m Ax is the amount of A in the x-direction Ay A = 10 m 30 o Ax Ay = Asinq = 10 sin(30) = 10(0. 5) Ay is the amount of A in = +5 m the y-direction x

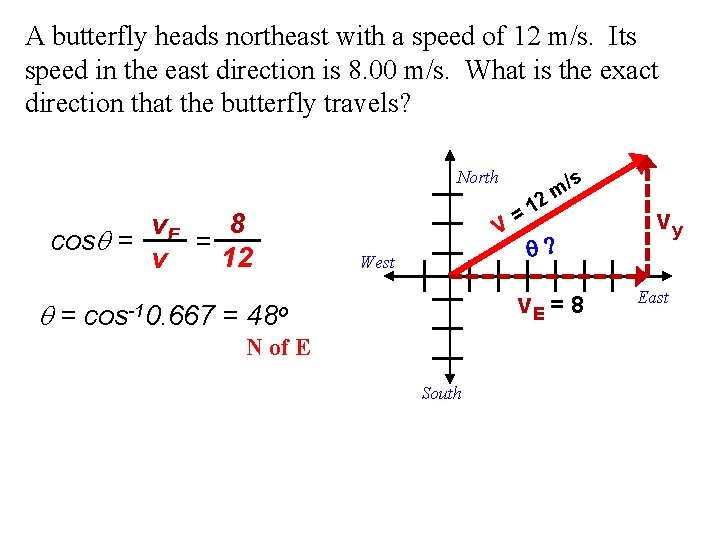
A butterfly heads northeast with a speed of 12 m/s. Its speed in the east direction is 8. 00 m/s. What is the exact direction that the butterfly travels? North 8 v. E cosq = = 12 v v West s / m 2 =1 q? v. E = 8 q = cos-10. 667 = 48 o N of E South vy East

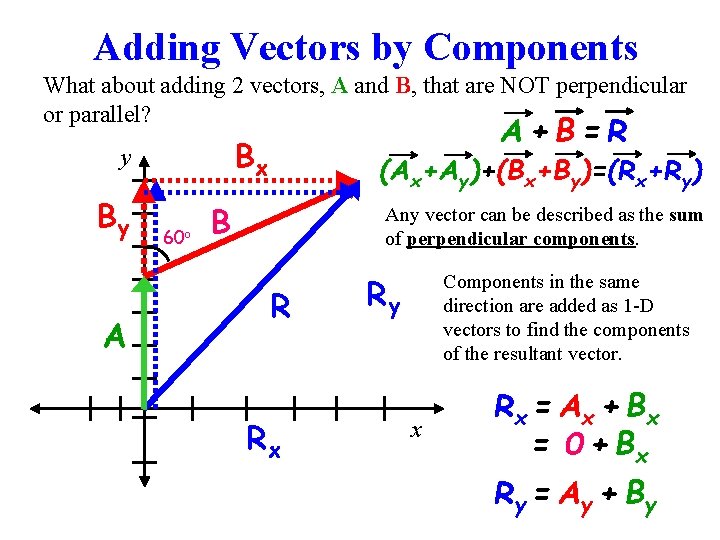
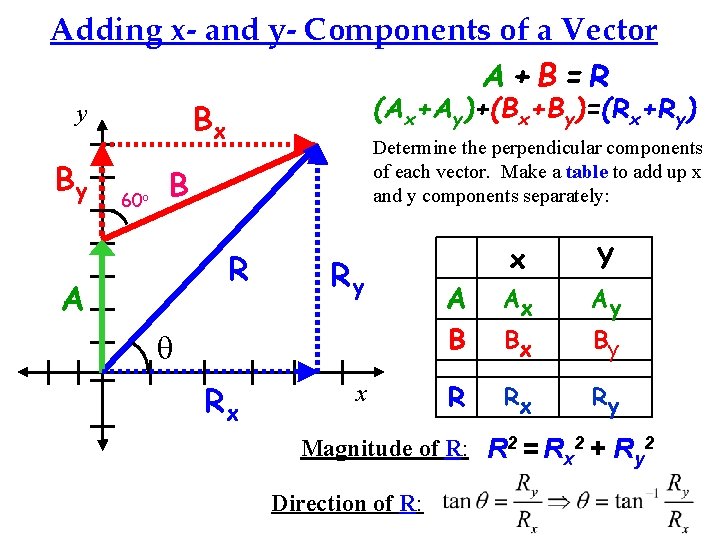
Adding Vectors by Components What about adding 2 vectors, A and B, that are NOT perpendicular or parallel? Bx y By A A+B=R 60 o (Ax+Ay)+(Bx+By)=(Rx+Ry) B Any vector can be described as the sum of perpendicular components. R Rx Ry Components in the same direction are added as 1 -D vectors to find the components of the resultant vector. x Rx = A x + B x = 0 + Bx Ry = A y + B y

Adding x- and y- Components of a Vector A+B=R (Ax+Ay)+(Bx+By)=(Rx+Ry) y Bx By 60 o Determine the perpendicular components of each vector. Make a table to add up x and y components separately: B R A Ry q Rx x x Y A B Ax Ay Bx By R Rx Ry Magnitude of R: R 2 = Rx 2 + Ry 2 Direction of R:

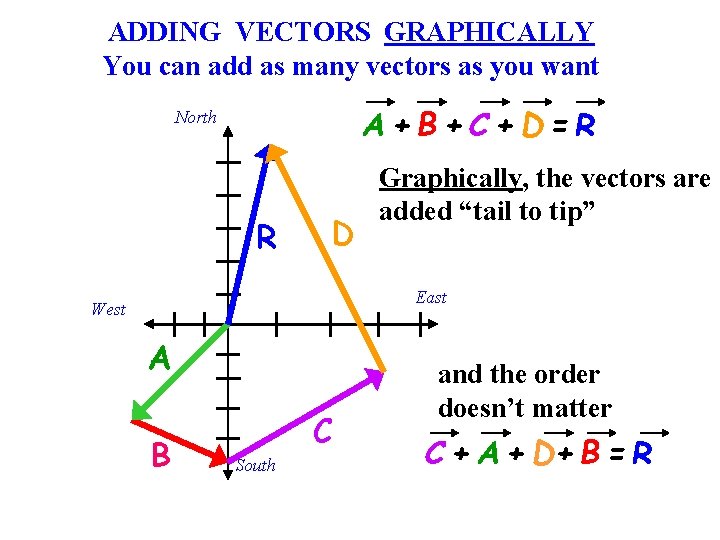
ADDING VECTORS GRAPHICALLY You can add as many vectors as you want A+B+C+D=R North R D Graphically, the vectors are added “tail to tip” East West A B C South and the order doesn’t matter C + A + D+ B = R

Mathematically ADDING VECTORS x Y A -Ax -Ay B +Bx -By C +Cx +Cy D -Dx +Dy R Rx Ry D A A + B + C +D = R (Ax+Ay)+(Bx+By)+(Cx+Cy)+(Dx+Dy)=(Rx+Ry) To Add Vectors by Components: 1. Place each vector at origin. Find the x- and y- components of each vector in the sum, and list them in a table. Make sure to include the direction of each component by hand. 2. Add all the x-components to find Rx. 3. Add all the y-components to find Ry. 4. Use Pythagorean Theorem and trigonometry to find the magnitude and direction of R. Magnitude of R: B C Direction of R: R 2 = R x 2 + R y 2

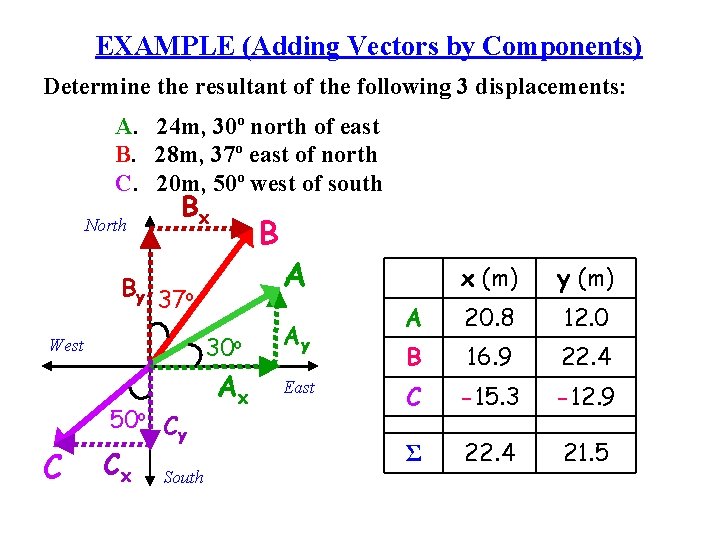
EXAMPLE (Adding Vectors by Components) Determine the resultant of the following 3 displacements: A. 24 m, 30º north of east B. 28 m, 37º east of north C. 20 m, 50º west of south North Bx B By 37 o 30 o West C 50 o Cy Cx South Ax A Ay East x (m) y (m) A 20. 8 12. 0 B 16. 9 22. 4 C -15. 3 -12. 9 Ʃ 22. 4 21. 5

EXAMPLE R North Ry q West Rx South East Magnitude x (m) y (m) A 20. 8 12. 0 B 16. 9 22. 4 C -15. 3 -12. 9 Ʃ R 22. 4 21. 5 Direction R = 31 m, 440 N of E (from the x-axis)

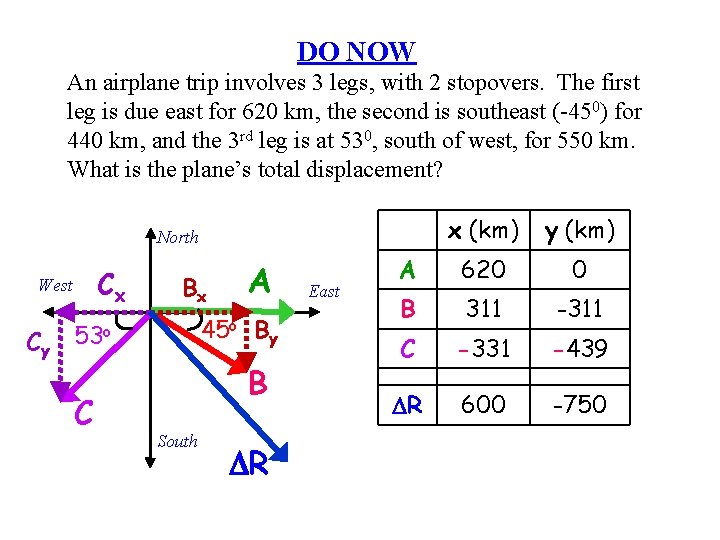
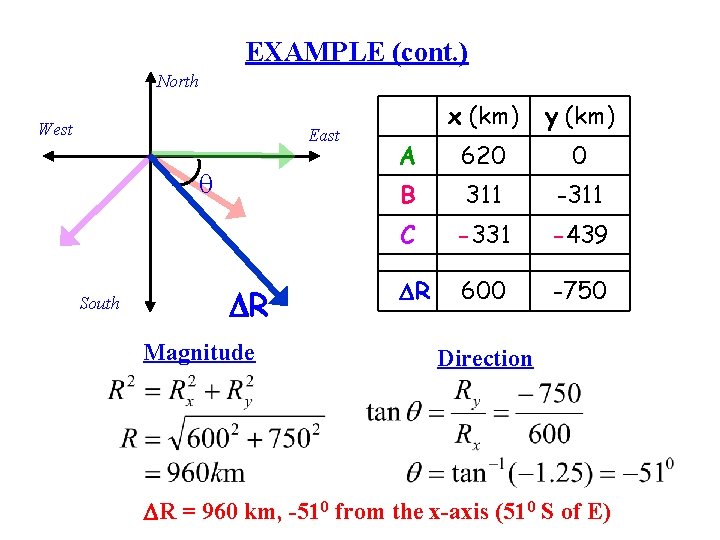
DO NOW An airplane trip involves 3 legs, with 2 stopovers. The first leg is due east for 620 km, the second is southeast (-450) for 440 km, and the 3 rd leg is at 530, south of west, for 550 km. What is the plane’s total displacement? x (km) y (km) A 620 0 B 311 -311 C -331 -439 DR 600 -750 North Cx West Cy Bx 45 o 53 o C A By B South DR East

EXAMPLE (cont. ) North West East q South DR Magnitude x (km) y (km) A 620 0 B 311 -311 C -331 -439 DR 600 -750 Direction DR = 960 km, -510 from the x-axis (510 S of E)

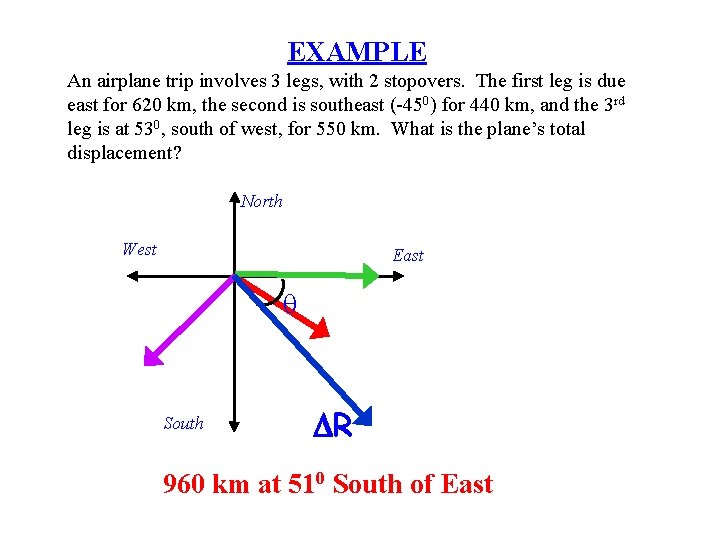
EXAMPLE An airplane trip involves 3 legs, with 2 stopovers. The first leg is due east for 620 km, the second is southeast (-450) for 440 km, and the 3 rd leg is at 530, south of west, for 550 km. What is the plane’s total displacement? North West East q South DR 960 km at 510 South of East

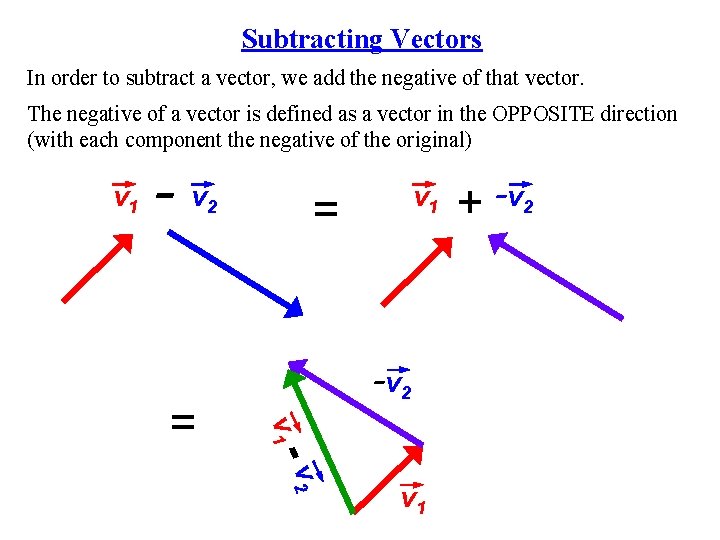
Subtracting Vectors In order to subtract a vector, we add the negative of that vector. The negative of a vector is defined as a vector in the OPPOSITE direction (with each component the negative of the original) v 1 -v v 1 = -v 2 v 1 - = 2 v 1 + -v 2

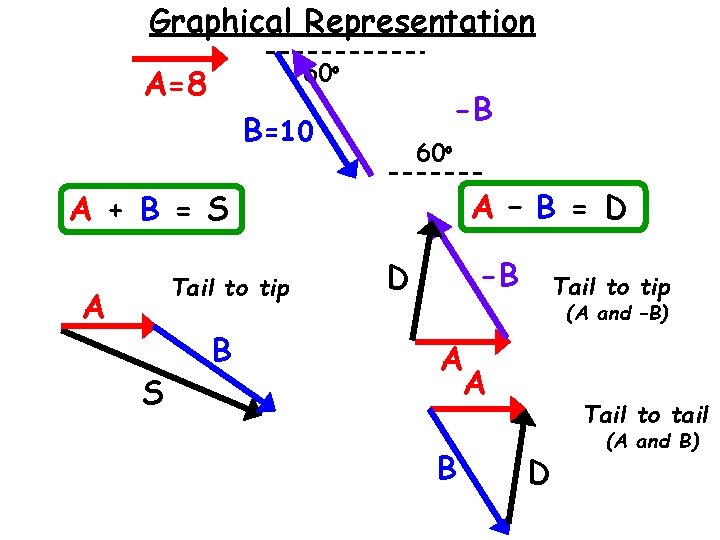
Graphical Representation 60 o A=8 -B B=10 60 o A – B = D A + B = S Tail to tip A S B -B D Tail to tip (A and –B) A A B Tail to tail D (A and B)

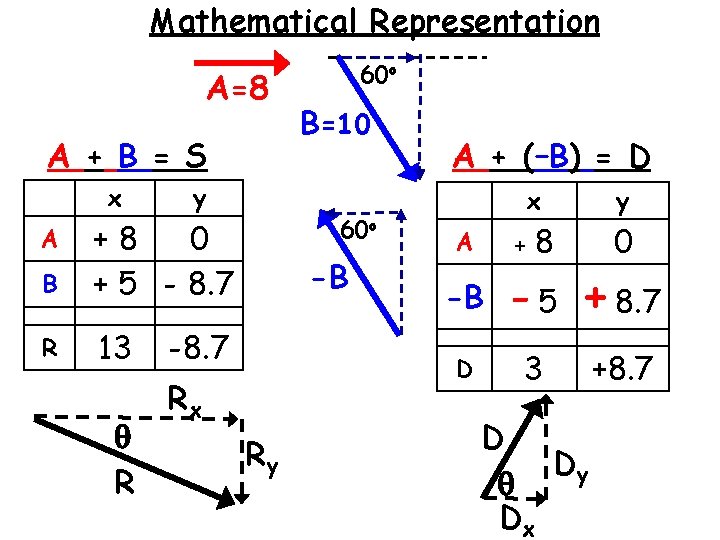
Mathematical Representation A=8 A + B = S x y B +8 0 + 5 - 8. 7 R 13 A q R 60 o B=10 60 o -B -8. 7 A + (–B) = D A -B D Rx Ry x y +8 0 3 +8. 7 - 5 + 8. 7 D Dy q Dx

Scalar Multiplication of a vector by a positive scalar changes the magnitude of the vector, but leaves its direction unchanged. The scalar changes the size of the vector. The scalar "scales" the vector. Multiplication of a vector by a negative scalar changes the magnitude of the vector, and makes the direction opposite. Example: 3 A = 3 x = = If the scalar is negative, it changes the direction of the vector. -3 A = -3 x = =